ЗВ и мобильная связь 2010. Запорізький національний технічний університет
 Скачать 37.31 Mb. Скачать 37.31 Mb.
|
|
1 тип (первичные, без переизлучателя): Потери передачи L - это отношение мощности, подводимой к передающей антенные 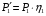 и мощности на выходе приемной антенны и мощности на выходе приемной антенны 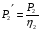 при распространении в реальных условиях при отсутствии тепловых потерь при распространении в реальных условиях при отсутствии тепловых потерь 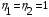 , при заданных G1 иG2. , при заданных G1 иG2.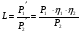 , (2.26) , (2.26)Подставив в (2.26) выражение (2.22) для 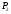 получим значение потерь передачи L для радиолиний первого типа получим значение потерь передачи L для радиолиний первого типа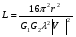  . (2.27) . (2.27) Расчеты упрощаются, если в L выделить составляющую Lb, Основные потери передачи Lbдля радиолиний первоготипа передачи Lb – характеризует потери в реальных условиях которые обусловлены сферической расходимостью фронта волны при условии что 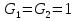 , ,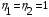 - обе антенны ненаправленные : - обе антенны ненаправленные :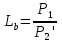 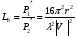 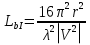 (2.28) (2.28) Сравнивая L и Lb замечаем, что потери передачи 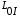 можно записать: можно записать: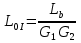 , (2.29) , (2.29)или в дБ: 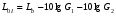 . .Для радиолиний 2 типа потери передачи L(ретранслятор находится в середине трассы) : Для радиолиний II типа потери линии передачи LII: 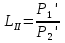 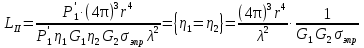 Выделим в выражении Lb – основные потери передачи 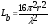 Для этого умножим и разделим LII на множитель 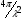 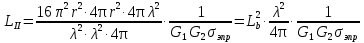 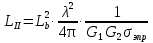 В реальных условиях потери передачи в этом случае будут равны 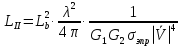 (2.30) (2.30)Потери в условиях свободного пространства 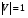 (transmissionlossinfreespace) (transmissionlossinfreespace)В условиях свободного пространства потери передачи L0 и основные потери передачи Lb0 определяются аналогично как для реальных условий, но считают 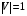 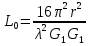  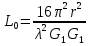 , , 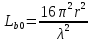 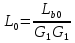 (2.31) (2.31)Область пространства, существенная для распространения радиоволн (зоны Френеля) При распространении радиоволн в однородном безграничном пространстве различные области этого пространства неодинаково влияют на процесс формирования поля в точке приема. Есть область пространства, которая грает определяющую роль. Область, в которой распространяется основная часть передаваемой мощности, называется существенной областью. Она охватывает пространство вблизи прямой, соединяющей точки излучения и приема.(рис. ) Определим конфигурацию и размеры существенной зоны.  Рисунок – Понятие существенной зоны Это можно сделать, исходя из принципа Гюйгенса – Френеля. Принцип Гюйгенса –Френеля. Согласно это принципу Гюйгенса каждый элемент dS в окрестности точки АВ поверхности S (рис. ) до которого в момент времени t дошла волна и, следовательно, в котором имеется электромагнитное возбуждение, рассматривается как воображаемый (виртуальный) вторичный источник, излучающий элементарную сферическую электромагнитную волну, с волновой поверхностью 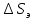 . .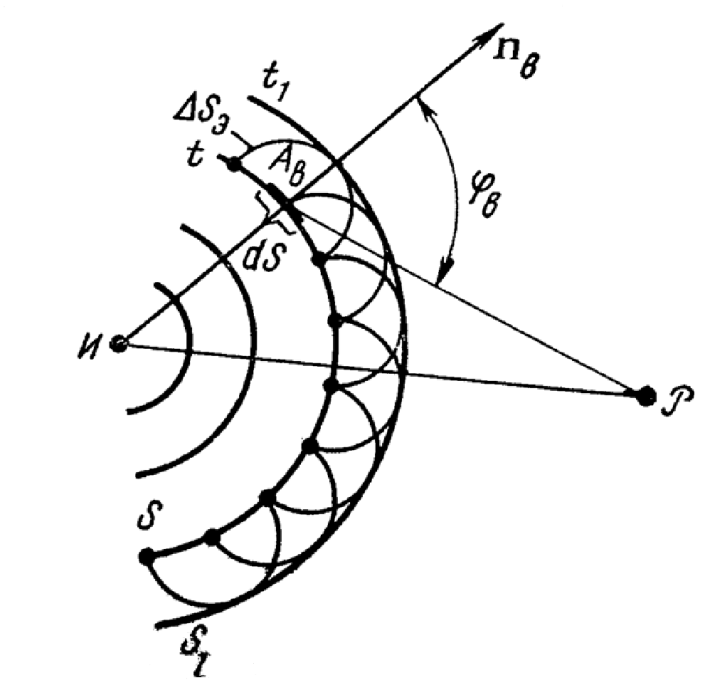 Рисунок - К принципу Гюйгенса–Френеля Огибающая S1 этих сферичных волн определяет положение волновой поверхности в более поздний момент времени t1.Таким образом, в соответствии с принципом Гюйгенса–Френеля поле в точке наблюдения Р представляется как результат наложения элементарных вторичных волн, излученных элементами волновой (или отражающей) поверхности. При сложении вторичных волн необходимо в точке наблюдения учитывать их амплитуду и фазу. Амплитуда зависит от угла φв между нормалью и рассматриваемому элементу волновой поверхности первичной волны 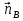 и направлением в точку наблюдения. и направлением в точку наблюдения.Вторичный излучатель как единичный излучатель не может быть физически реализован, так как реально проявляется только интегральный эффект вторичных излучателей. В этом смысле единичный излучатель понимается как некоторый воображаемый излучатель. Первым шагом для определения существенной зоны является разделение пространства на зоны Френеля. Зоны Френеля. Построение, предложенное Френелем позволяет наглядно истолковать принцип Гюйгенса. Пусть в точке А расположен излучатель, а в точке В – приемная антенна. Расстояние между ними r>>λ(дальняя зона). На расстоянии r1 расположим бесконечную плоскость S, перпендикулярную линии АВ. На этой поверхности будем рассматривать вторичные источники (виртуальные). Построим серию ломаных АDnВ, пересекающих зту плоскость S. 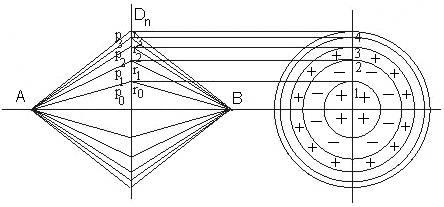 Рисунок - Зоны Френеля на плоскости: а) построение зон; б) границы зон на плоскости S Длина каждой последующей ломаной должна быть больше предыдущей на 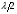 рабочей длинны волны. В обозначениях рисунка это условие будет выглядеть так: рабочей длинны волны. В обозначениях рисунка это условие будет выглядеть так: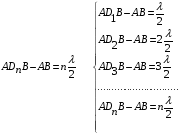 , ( ) , ( )где n – целое число. Это условие ( ) будет определять максимальные и минимальные значения напряженности поля в точке В. При n – нечетных будут максимумы, а n-четные –минимумы. Семейство отрезков АDn и DnВ очерчивают в пространстве коническую поверхность, линия пересечения которой с плоскостью S является окружностью с центром в точке О. Отрезки всех ломаных образуют систему окружностей на S. Вид окружностей приведен на рисунке (рис). Участки плоскости, ограниченные окружностями называется зонами Френеля на плоскости. Первая зона – круг. Зона высших порядков – кольцевые области. Во всех точках фронта по определению поле имеет одну и туже фазу, эквивалентные источники, расположены на фронте, возбужденной волны синфазно. Но от различных точек фронта вторичные волны приходят в точку В в различных фазах, так как удалены от точки В на разные расстояния. При этом сдвиг фаз между суммарными полями, созданными соседними зонами составляет 180о. Последовательные зоны маркируются знаками «+» и «-» (разность входа составляет 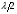 . .Амплитуда поля в точке В, создаваемая каждой зоной уменьшается по мере увеличения ее номера. Это объясняется, что зоны с высшими номерами видны из точки В под меньшим углом. Амплитудные и фазовые соотношения. Суммарное поле, создаваемое всеми зонами Френеля можно определить, если просуммировать волны, создаваемые элементами поверхности dS , находящимися в пределах каждой зоны в отдельности, а затем найти суммарное поле, обусловленное всеми зонами Френеля. Если разделить каждую зону Френеля на некоторое число равных по площади концентрических колец, то эти волны, создаваемые каждым кольцом не будут отличаться друг от друга по амплитуде так как АВ>>λ. будут отличаться только по фазе. Например, если первую зону Френеля разделить на 10 колец то фазы колебаний источников двух соседних колец будут отличатся друг от друга на 18о. Геометрическое сложение колебаний можно изобразить в виде векторной диаграммы, а результирующий вектор для I зоны обозначить 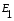 (рис., а) (рис., а)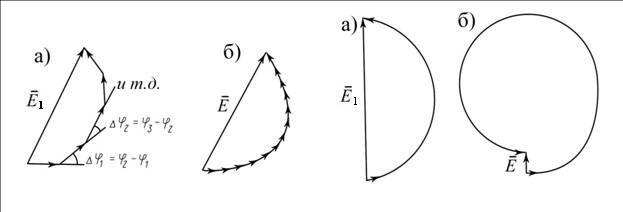 Рисунок 1 Рисунок 2 Рисунок 1- Векторное суммирование полей от различных участков отверстия: а) при скачкообразном, б) при плавном изменении его диаметра Рисунок 2 - Векторное диаграмма при диаметре отверстия , соответствующим: а) первой зоне Френеля, б) второй зоне Френеля Если приращение от кольца к кольцу невелико, то можно вместо ломанной линии получить плавную (рис., а). Результирующий вектор второй зоны Френеля 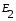 будет направлен противоположно будет направлен противоположно 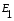 и по длине будет короче, вследствие увеличения расстояний АДn и ДnВ то есть и по длине будет короче, вследствие увеличения расстояний АДn и ДnВ то есть 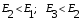 и т.д. и разность фаз будет равна 180о. и т.д. и разность фаз будет равна 180о.Суммирование можно представить в виде скручивающейся спирали. Отрезок между началом А и концом стрелки показывает величину результирующего колебания при перемещении по спирали. При приближении к фокусу спирали результирующая амплитуда колебания приближается к 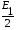 (рис). (рис).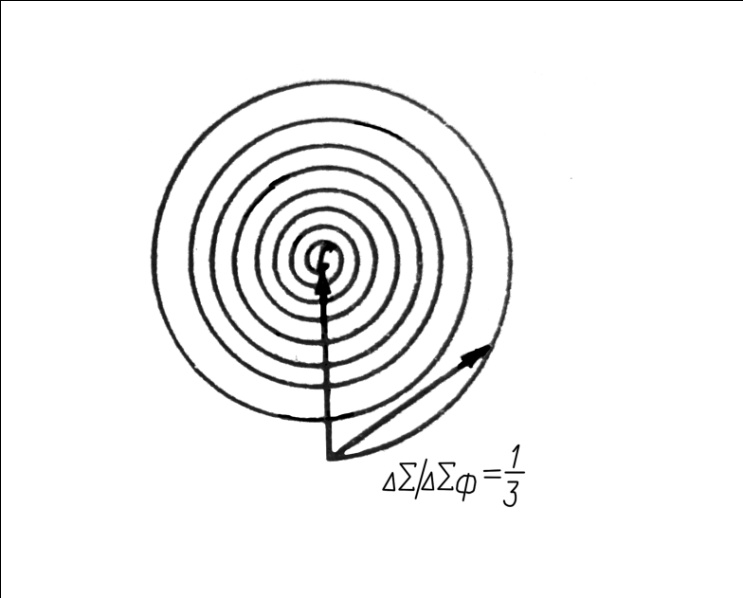 Рисунок - Векторная диаграмма при увеличении диаметра отверстия до бесконечных размеров Так как фазы соседних зон отличаются на 180о и векторы 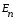 коллинеарны, то геометрическое суммирование сводится к алгебраическому. коллинеарны, то геометрическое суммирование сводится к алгебраическому.Разделение плоскости S на зоны Френеля дает возможность представить результирующую амплитуду волн вторичных источников всех зон в виде знакопеременного сходящегося ряда 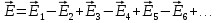 ( ) ( )Соседние члены этого ряда мало отличаются друг от друга и поэтому каждый из членов можно считать равным среднему арифметическому из двух соседних членов. Тогда ряд записывается 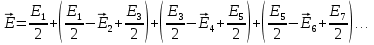 ( ) ( )При 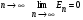 , то величина в скобках близка нулю, то тогда результирующий вектор , то величина в скобках близка нулю, то тогда результирующий вектор 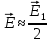 , то есть половине значения напряженности поля, создаваемой первой зоной Френеля. Другая половина , то есть половине значения напряженности поля, создаваемой первой зоной Френеля. Другая половина 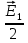 , а также поля, создаваемые зонами Френеля высших номеров компенсируются взаимно. , а также поля, создаваемые зонами Френеля высших номеров компенсируются взаимно.Графически можно представить результат в виде осциллирующей кривой (рис.). 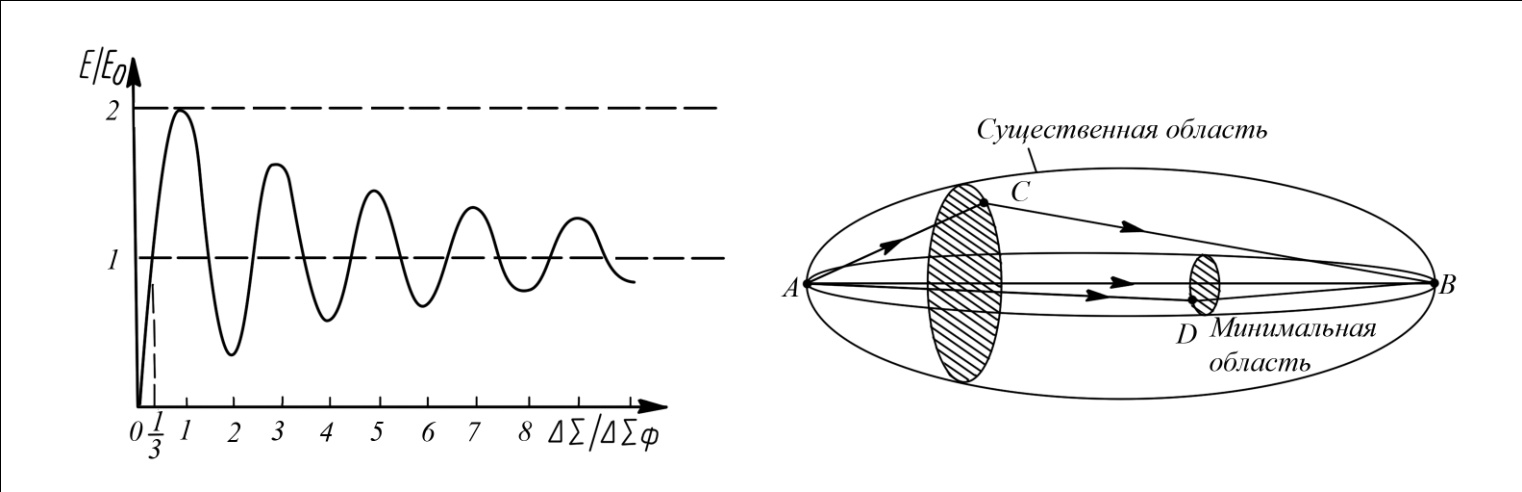 Рисунок - Зависимость 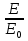 от радиуса зон Френеля от радиуса зон ФренеляТаким образом результирующее поле в точке наблюдения в основном создается волнами вторичных излучателей, расположенными в пределах первых нескольких зон Френеля (n=6-8 зон). Вклад остальных зон очень мал, в силу быстрой сходимости ряда ( ). Размеры зон Френеля. Определим радиусы зон Френеля. Обозначим ρn радиус n-зоны. Геометрия задачи представлена на рисунке 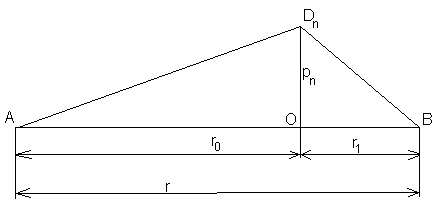 Рисунок - Определение радиусов зон Френеля Из рисунка ( ) из простых геометрических соображений находим: 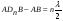 Из 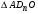 : : ( ) Учитывая, что на практике всегда выполняются условия что r0>>λ и r1>>λ, то радикал в уравнении ( ) можно разложить биноминальный ряд вида 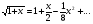 Так как x<<1 то в этом разложении берем первых два члена, тогда 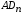 из ( ) будет равно из ( ) будет равно 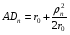 ( ) ( )Из 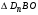 : :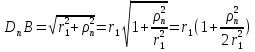 Аналогично определению 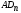 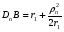 ( ) ( )Используя условие 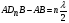 , получаем уравнение для определения радиуса n-ой зоны Френеля , получаем уравнение для определения радиуса n-ой зоны Френеля 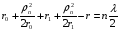 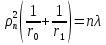 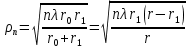 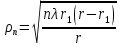 ( ) ( )Первая зона Френеля – круг с радиусом 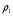 достигает максимального значения на середине трассы. достигает максимального значения на середине трассы.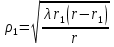 , ( ) , ( )а зоны Френеля с номером 2 и более – кольца, внешний радиус которых определяется ( ). Площади всех зон Френеля одинаковы и имеют величину 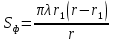 . ( ) . ( )Если 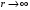 , а r1 – остается конечным, то , а r1 – остается конечным, то 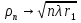 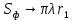 Конфигурация существенной зоны. Пространственные зоны Френеля. Минимальная зона Понятие существенной и минимальной областей пространства необходимы для рассмотрения процессов распространения радиоволн при наличии границ разделов двух сред, механизма распространения радиоволн в неоднородной среде и т.д. Определение конфигурации существенной и минимальной зон можно сделать следующим образом. Если менять расстояние r1 , т.е. плоскость S будет перемещаться вдоль линии наблюдения АВ, то согласно формуле 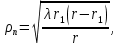 радиус зон Френеля будут меняться и на плоскости чертежа мы получим эллипсы с фокусами в т.А и в т.В , каждый из которых будет определять соответствующую зону Френеля. В пространстве для каждой зоны Френеля получим соответствующие эллипсоиды вращения вокруг линии АВ (рис ). Чем меньше длина волны при фиксированном значении расстояния r0+r1=r между излучателем и точкой наблюдения, тем больше число n зон Френеля, образующих существенный участок интегрирования. Пространственные зоны Френеля. Для любого положения плоскости S будет справедливо равенство, описывающие границу данной зоны Френеля 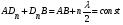 ( ) ( )А это уравнение эллипсоида вращения с фокусами в точках А и В. В пространстве первая зона Френеля представляет собой вращение , а зона Френеля высших порядков – это пространство между двумя эллипсоидами вращения (рис. ). 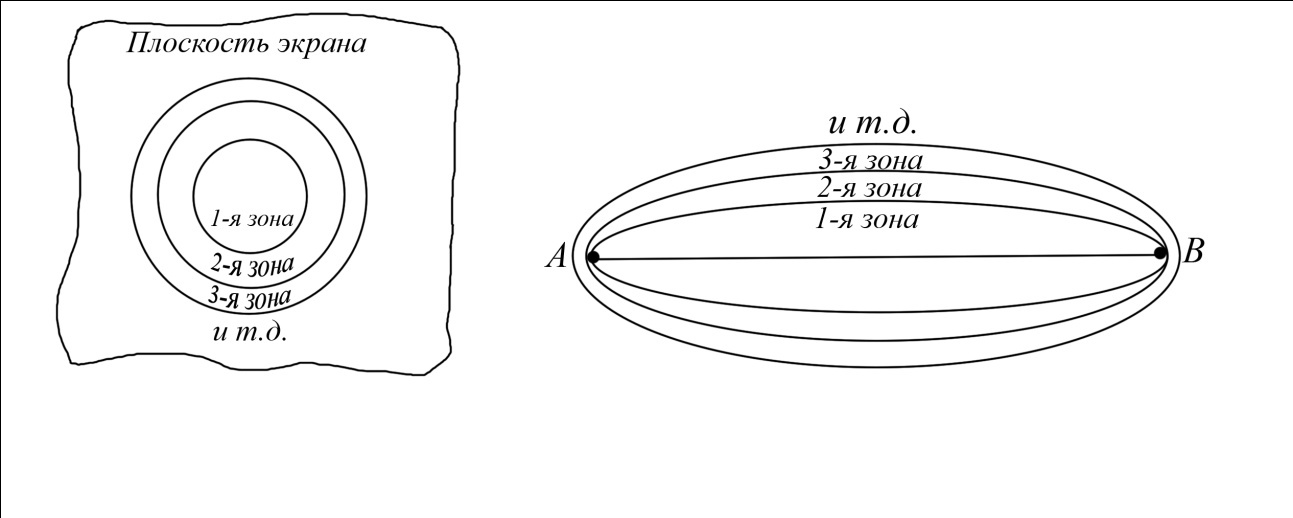 Рисунок – Эллипсы соответствующих зон Френеля Отсюда сделаем важный вывод: о наличии области пространства, существенно участвующей в распространении радиоволн. Эта область ограничена эллипсоидом, соответствующим внешней границе пространственной зоны Френеля с небольшим номером. Существенная область при распространении радиоволн в однородной среде представляет собой эллипсоид вращения с фокусами в точках А и В ( передача – прием) для которых выполняется условие 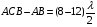 , ( ) , ( )то есть эта область ограничена зонами Френеля нескольких начальных номеров. Часто для упрощения считают, что существенная область при распространении радиоволн, является область, ограниченная эллипсоидом с поперечным сечением, равным первой зоне Френеля (рис ).  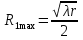 Минимальная область пространства – эллипсоид вращения, конфокальной существенной области и являющийся геометрическим местом точек для которых выполняются условие 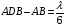 ; ( ) ; ( )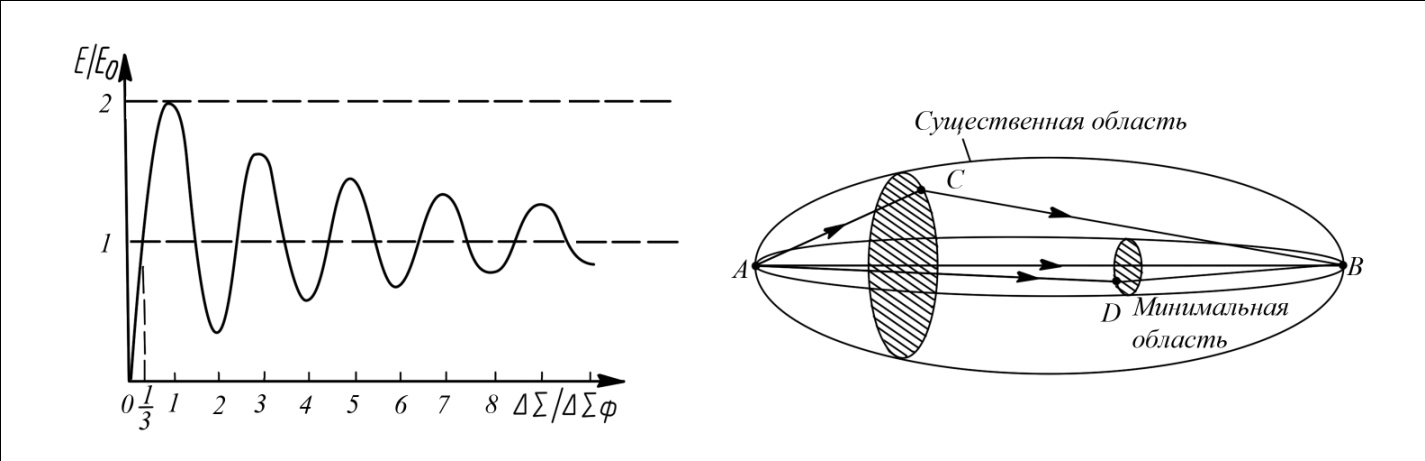 Рисунок – Существенная и минимальная области пространства Так как в реальных условиях расстояние между корреспондирующими пунктами всегда намного больше λ, то эллипсоиды существенных и минимальных зон сильно вытянуты. В пределе, при λ→0 они выражаются в прямую линию, что соответствует лучевым представлениям геометрической оптики. Таким образом энергия радиоволны передается не по нитевидному каналу, а в пределах вполне конкретного объема пространства, имеющего форму эллипсоиды вращения и ограниченного первой зоной Френеля. Понятия о существенных и минимальных зонах потребуется в дальнейшем при объяснении процессов отражения радиоволн от неровной поверхности раздела дуги сред; при распространении радиоволн в средах с неоднородными электрическими параметрами. Распространение земных волн. Электрические свойства Земли, как любой среды оцениваются εrзм, μrзм, σзм Все виды земной поверхности обычно считают немагнитными μrзм=1, а εrзм, σзм будут изменятся в широких пределах при изучении условий распространения радиоволн. Составляющими земных покровов являются различные виды почв, водная поверхность (пресная вода рек , озер), морская вода, вода в виде снега и льда, лес. Почва. На электрические свойства основное влияние оказывает не химический состав, а способность поглощать влагу и удерживать ее. Например, суглинок в естественных условиях σ =10-2см/м в сухом состоянии ведет себя как гранит σ =10-4см/м. в течении года содержание влаги в верхних толщах Земли меняется до глубины 1 м, а ниже влажность постоянна. Вода. Электрические свойства воды зависят от ее солености. С увеличением солености растет σ в Условно рассматривают воду морскую и пресную, хотя содержание солей в воде различных морей не одинаково. Вода пресных водоемов содержит примеси. Растительность, снег, лед, покрывающие почву, могут рассматриваться как полупроводящие слои, лежащие на поверхности почвы. Эти покровы особенно влияют на см и мм волнах. В таблице приведены ориентировочные значения εrзм, γзм различных земных покровов. Таблица 3.1
Величины εrзм, σ зм не дают полной характеристики условий распространения радиоволн в Земле и вдоль ее поверхности. Среды разделяют на диэлектрики и проводники в курсе распространения радиоволн не по εrзм, σ зм , а по соотношению плотностей токов смещения Jсм и тока проводимости Jпр 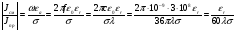 . .По отношению к земной поверхности критерием разделения ее на диэлектрики, полупроводники и проводники будет являться соотношение между действительной и мнимой частью комплексной диэлектрической проницаемостью земли, а именно 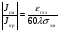 ( ) ( )Если 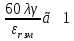 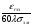 >> 1 то земную поверхность можно считать диэлектриком; >> 1 то земную поверхность можно считать диэлектриком;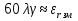 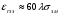 - земная поверхность полупроводник; - земная поверхность полупроводник; 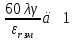 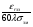 << 1 – земная поверхность по свойствам приближается к проводнику. << 1 – земная поверхность по свойствам приближается к проводнику.Если 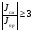 - то почва диэлектрик, и если - то почва диэлектрик, и если 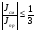 то почва проводник. то почва проводник.Электрические свойства земной поверхности удобно оценивать относительной комплексной диэлектрической проницаемостью: 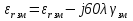 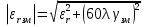 В условиях реальной земной поверхности 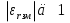 Обычно 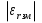 не бывает больше 10 и только в исключительных случаях 2—5 (сухой песок в см – диапазоне) не бывает больше 10 и только в исключительных случаях 2—5 (сухой песок в см – диапазоне)Граничные условия Щукина -Леонтовича Дифракционная задача о распространении радиоволн вдоль Земли решается с помощью приближенных граничных условий Щукина-Леонтовича, вместо точных граничных условии. На границе раздела в воздухе соотношение между касательными составляющими 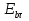 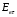 и и 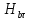 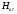 определяется волновым сопротивлением почвы определяется волновым сопротивлением почвы 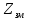 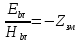 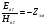 Где 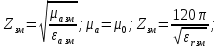 Граничные условия Щукина – Леонтовича упрощают задачу нахождения поля земной волны путем решения системы уравнений Максвелла только для воздуха, вместо решения двух систем – для Земли и воздуха, при использовании точных граничных условий. 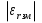 зависит от длины волн и ведет себя по разному на различных длинах волн( смотри табл.3.2). зависит от длины волн и ведет себя по разному на различных длинах волн( смотри табл.3.2).Таблица 3.2
Коэффициенты отражения при вертикальной и горизонтальной поляризации. Земная поверхность отражает радиоволны и это связано со значениями относительной комплексной диэлектрической проницаемости. Отражение характеризуется коэффициентом отражения 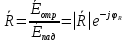 На границе раздела воздух – земля, при расчете коэффициента отражения считают, что воздух обладает параметрами свободного пространства. Угол возвышения, или угол встречи (Δ). Введем понятие угла возвышения, или угла встречи, или угол скольжения Δ=90-φ, где φ – угол падения 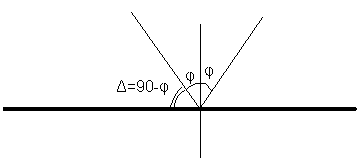 Рисунок - К определению угла возвышения  Тогда если воздух – свободное пространство, а почва – диэлектрик с  εr, то коэффициенты отражения для горизонтальной и вертикальной поляризации εr, то коэффициенты отражения для горизонтальной и вертикальной поляризации 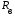 и и 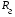 будут иметь вид: будут иметь вид:Горизонтальная поляризация Коэффициент отражения при горизонтальной поляризации имеет вид: 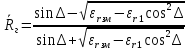 . ( ) . ( )При 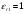 - воздух - воздух 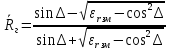 , ( ) , ( )Где εrзм - комплексная величина. Из ( ) видно, что 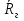 зависит от λ и от параметров почв, т.е. от соотношения зависит от λ и от параметров почв, т.е. от соотношения 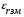 и и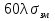 . Проанализируем . Проанализируем 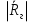 для трех видов почв: для трех видов почв: |
