ЗВ и мобильная связь 2010. Запорізький національний технічний університет
 Скачать 37.31 Mb. Скачать 37.31 Mb.
|
|
Распространение УКВ в городах имеют две основные особенности:
Повышенное ослабление обусловлено большим количеством препятствий типа каменных и железобетонных зданий, большого количества проводов, крыш зданий и др. Потери оценивают статистически, разделяя районы города на два типа: – густо застроенные высотными зданиями; – районы, застроенные в основном двух и трехэтажными зданиями.
Большая неоднородность поля в различных точках наблюдения обусловлена интерференцией большого числа волн, отражённых от различных препятствий в пределах города. Измерения показали, что уровень отражённых сигналов составляет 50 – 60 % от прямого сигнала. Это сильно искажает передаваемое изображение (многоконтурность). К тому же отражения изменяют первичную поляризацию поля. Например, передающая станция работает с горизонтальной поляризацией сигнала, а при приёме в городских условиях обнаруживается вертикальная составляющая, которая равна 30 % от уровня горизонтальной составляющей. Для высококачественного приёма необходимо применять наружные антенны коллективного пользования с большим коэффициентом усиления и оптимально располагаться в конкретных условиях. Грубую оценку среднего уровня напряжённости поля можно делать по формуле Введенского, вводя множитель (0,4 ÷ 0,6). Схема распространения УКВ в таких условиях имеет вид: 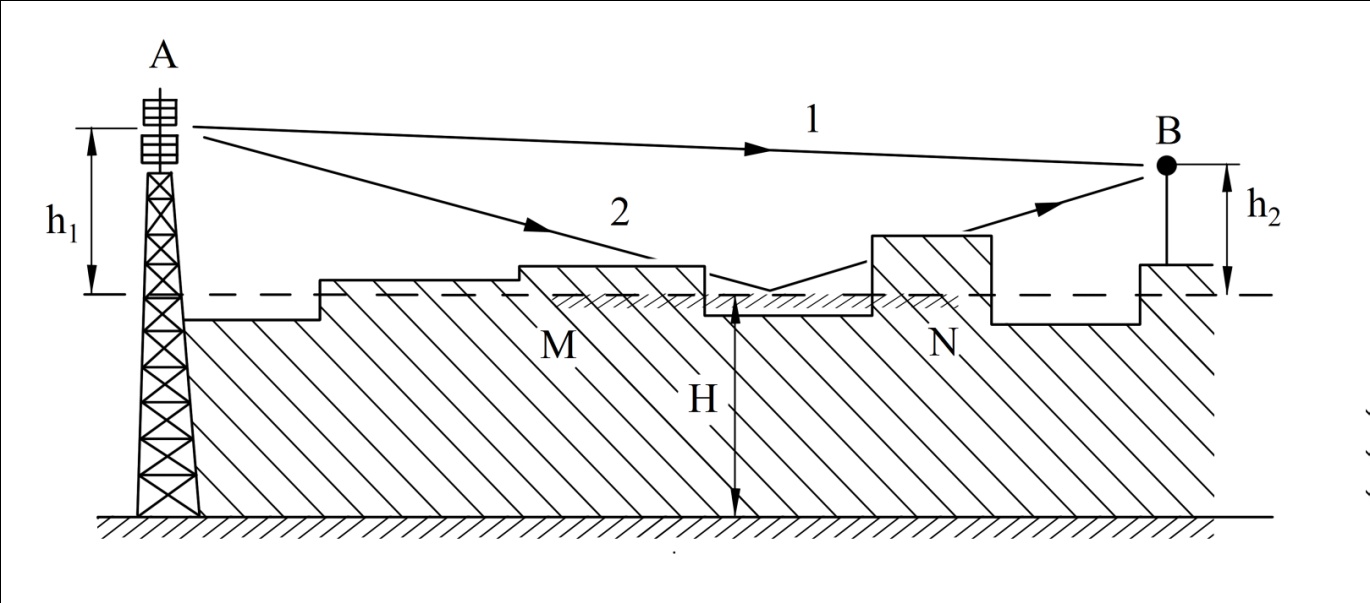 Рисунок - Распространение УКВ в условиях города при наличии прямой видимости между передающей и приемной антеннами В приёмную антенну приходят прямая и отражённая волны. Зная высоты антенн h1 и h2, необходимо установить границы первой зоны Френеля. Эти границы обозначены линией MN. Если эта область приходится на застроенную часть города, то необходимо оценить среднюю высоту крыши Н в этом районе. Поле можно рассчитать по интерференционным формулам, считая под высотами антенн – высоты, отсчитываемые относительно этого среднего уровня h1’ и h2’. Это допущение возможно, т.к. при скользящем падении металлические крыши являются хорошими отражателями. Расчёт напряжённости электрического поля в городских условиях. Модели расчёта Модель Бардина - Дымовича С учетом среднего уровня высоты застройки с уровнями подъёма передающей и приёмной антенны, Бардин и Дымович используя экспериментальные данные, на основании принципа Гюйгенса и Френеля получили эмпирические формулы для расчёта поля УКВ, учитывающие размеры улиц и их расположение относительно передающей станции. Наиболее интересным есть случай плотной застройки, т.е. необходимо проводить оценку для наихудших условий распространения, т.е. для приёма на поперечных улицах (перпендикулярных к линии, соединяющей передатчик и приёмник). Предполагалось, что стены здания являются абсолютно поглощающими и не оказывают влияния на Е в точке приёма. Решая дифференциальную задачу вариационным методом и используя приближённый способ вычисления быстро осциллирующих интегралов, получили простую формулу для напряжённости поля на поперечных улицах 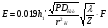 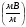 , ,где Р – мощность передатчика, подводимая к антенне; D – коэффициент усиления антенны; h1’ – высота передающей антенны, отсчитываемая от уровня крыш в месте приёма; r – расстояния от исследуемой точки до передающей станции; λ – длина волны; Z – расстояние от приёмника до уровня крыш зданий; b – половина ширины улицы F. 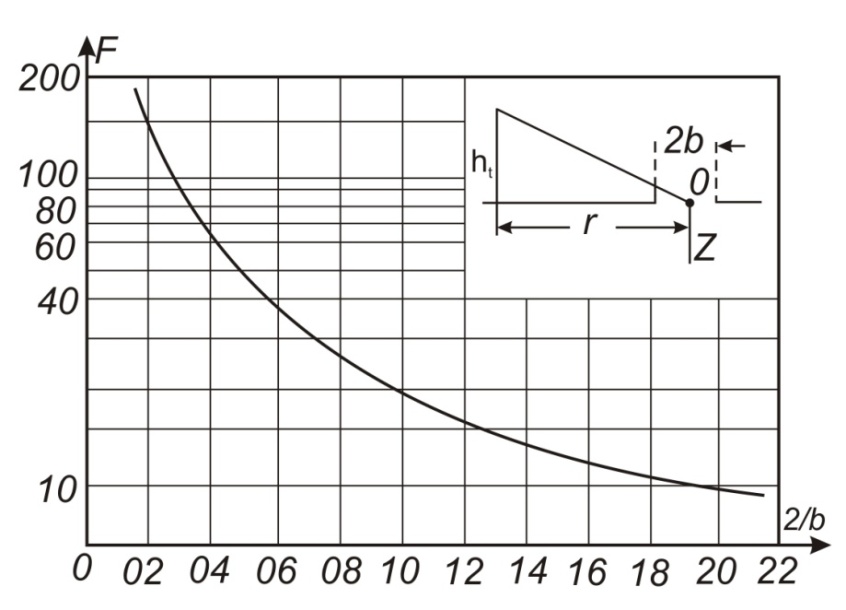 Рисунок - График зависимости 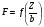 - дополнительный множитель. - дополнительный множитель.F 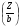 - дополнительный множитель, определяемый по графику на рис. 5.1. предполагалось, что Z >> λ, b >> λ. Формула даёт неплохое совпадение с экспериментом. - дополнительный множитель, определяемый по графику на рис. 5.1. предполагалось, что Z >> λ, b >> λ. Формула даёт неплохое совпадение с экспериментом. Модель Трифонова Трифонов путём переработки экспериментальных данных для большого города получил формулы для расчёта средней напряжённости в случае, если приёмная антенна расположена на высоте 1,5 м, а передатчик выше крыши домов 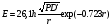 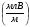 для f = 150 МГц для f = 150 МГц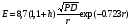 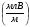 для f = 300 МГц для f = 300 МГцР в Ваттах – мощность передатчика r – (км) расстояние h – высота приёмной антенны над уровнем земли D – высота приёмной антенны над передающей антенной Хорошие результаты только получаются до  Эмпирическая модель Олсбруна - Парсона Она разработана по полученным Окамурой графикам. Эта модель позволяет рассчитать «потери передачи» L 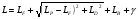 , где , где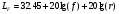 - потери передачи в свободном пространстве, дБ; - потери передачи в свободном пространстве, дБ;f – рабочая частота в МГц; r – расстояние между антеннами базовой и мобильной станций в км; 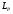 - потери распространения над плоской землёй (при необходимости с учётом атмосферной радиации), дБ. - потери распространения над плоской землёй (при необходимости с учётом атмосферной радиации), дБ.В большинстве случаев они могут быть вычислены по формуле, соответствующей квадратичной формуле Введенского 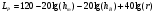 , где , гдеhm – высота мобильной антенны; hв – высота базовой антенны; 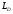 - дифракционные потери, в дБ, обусловленные характером рельефа местности под городской застройкой (холмистость местности, сферичность земли и т.п.) - дифракционные потери, в дБ, обусловленные характером рельефа местности под городской застройкой (холмистость местности, сферичность земли и т.п.)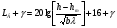 – потери, – потери, вызванные наличием городской застройки, дБ. 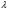 – длина волны; – длина волны; b – глубина улицы, на которой расположена мобильная антенна, м; h – средняя высота домов вблизи мобильной антенны, м; 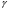 - поправочный коэффициент, зависящий от частоты, причём - поправочный коэффициент, зависящий от частоты, причём 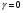 для для 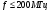 , а для , а для 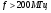 определяется по специальному графику в [ ]«связь с подвижными объектами в диапазоне СВЧ /Под ред. Х.И. Джейкса. М.: Связь 1979. – 520с. определяется по специальному графику в [ ]«связь с подвижными объектами в диапазоне СВЧ /Под ред. Х.И. Джейкса. М.: Связь 1979. – 520с.Для квазиплоского города, когда дифракционные потери равны нулю, основная формула упрощается и принимает вид 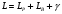 Расчёт по этим формулам дают достаточно хорошее совпадение с результатами Окамуры. Эмпирическая формула Хаты (Hata) Эта наиболее удачная и подробная аналитическая модель, полученная прямой аппроксимацией кривых Окамура. Но они не охватывают всех результатов, полученных Окамура справедлива для квазиплоского города при следующих ограничениях: f = 150…1500 МГц; hвs = 30…200 м - высота базовой станции, превышающая усредненную высоту рельефа в направлении анализируемой трассы в пределах 3 – 15 км; hms = 1…10 м; r = 1…20 км - расстояние от передатчика до приёмника. Средние потери передачи можно рассчитать по формуле 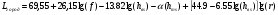 , (дБ) , (дБ)где 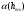 - поправочный коэффициент, используемый при высоте мобильной антенны hm, отличной от эталонной, равной 1,5 м (в эксперименте Окамура hms = 3 м). - поправочный коэффициент, используемый при высоте мобильной антенны hm, отличной от эталонной, равной 1,5 м (в эксперименте Окамура hms = 3 м).Выражения 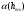 получаются различными для крупных и средних городов. получаются различными для крупных и средних городов.– Для города средних размеров 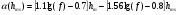 , (дБ) , (дБ)– Для крупного города 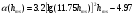 , (дБ) для , (дБ) для 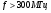 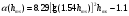 ,(дБ) для ,(дБ) для 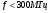 – Для сверх урбанизированных городов 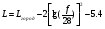 , (дБ). , (дБ).– Для открытых районов (пригород) 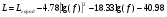 , (дБ). , (дБ).Эти формулы позволяют определить потери передачи с точностью до 7…17 дБ для дальностей больше 1 км. Модель Ли Ли (англ. W.C.Y.Lee) предложил очень простую модель распространения сигналов, основанную на серии проведенных в США измерений на несущей частоте fc=900 МГц. Согласно Ли, среднее значение мощности, измеренной на расстоянии r от передающей станции описывается выражением 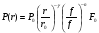  , ,или в логарифмическом представлении  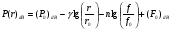  , ,где P0 - эталонная медианная мощность, измеренная на расстоянии r0=1 км; F0 – поправочный коэффициент, вычисляемый на основе серии множителей по формуле  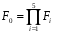 , ,в котором коэффициенты Fi рассчитывается следующим образом: 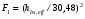 , ,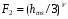 , ,где hbs, eff - эффективная высота базовой станции, (м). hms – высота антенны подвижной станции, (м). ν – показатель степени. При высоте антенны подвижной станции (мобильной) hms < 3 м принимается ν=1, а при высоте hmsболее 10 метров- ν=2 . В свою очередь 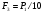 , ,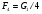 , ,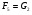 , ,где Р1 – мощность сигнала, излучаемого передатчиком, Вт G1,G2 – коэффициенты усиления базовой и подвижной станции относительно полуволнового вибратора. Параметры P0 иγ получены экспериментально на основе проведенных замеров в различных типах окружающей среды (табл.) Таблица Значения P0 иγ для различных типов окружающей среды
Медианные потери мощности в зависимости от частоты часто определяются коэффициентом  и его показателем степени n. и его показателем степени n.Для частот от 30 МГц до 2 ГГц и расстояний между подвижной и базовой станциями от 2 до 3 км, значение n лежит в пределах от 2 до 3. Величина n зависит от топографических особенностей местности. Для пригородов и сельских районов n=2 при частотах ниже 450 МГц и n=3 на частотах выше 450 МГц. На пересеченной местности эффективная высота антенны может сильно отличатся от ее физической высоты. На рис. 3.11 показаны способы ее определения. 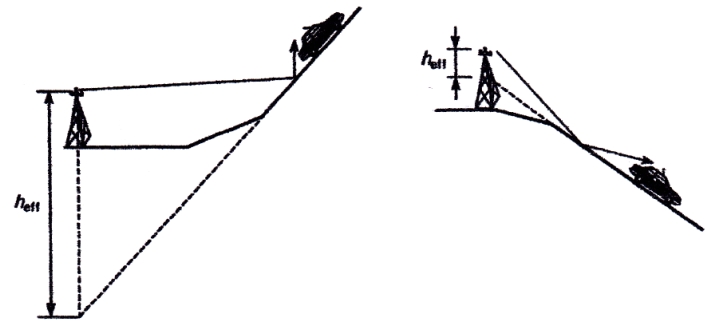 Рисунок 3.11 Определение эффективной высоты антенны базовой станции в холмистой местности Измерение, лежащие в основе эмпирических формул модели Ли, были проведены в системе со следующими параметрами: fc = 900 МГц hbs = 30,48 м G1 = 6 дБ P1 = 10 Вт hms = 3 м G2 = 0 дБ Модель Okamura В основе модели лежит множество измерений. Впервые она была представлена в работе [13]. Многочисленные измерения в частотном диапазоне от 150 до 1920 МГц проводились в Токио. Для определения средних потерь 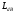 от расстояния r до передающей антенны базовой станции была предложена формула от расстояния r до передающей антенны базовой станции была предложена формула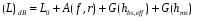 , ,где 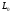 - потери при распространении в свободном пространстве - потери при распространении в свободном пространстве 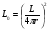 , вычисляемые в логарифмическом масштабе. , вычисляемые в логарифмическом масштабе.А(f,r) - среднее значение потерь в городской среде с квазигладкой земной поверхностью по отношению и затуханию в свободном пространстве в случае, если hbs = 200 м, а hms =3 м. G(hbs,eff) – корректирующий коэффициент в дБ, учитывающий отличие эффективной высоты базовой станции от 200 м; G(hms) – корректирующий коэффициент в дБ, учитывающий отличие высот подвижной станции, если она отличается от 3м. Формула для расчета (L)дБ совместно с рис. 13, рис. 3.13, рис. 3.14 позволяет оценить затухание сигнала в условиях городской застройки на частотах от 150 до 2000 МГц. При условии что расстояние между передающей и приемной антеннами составляет от 1 до 100 км, а эффективная высота базовой станции лежит в диапазоне от 30 до 1000 м. 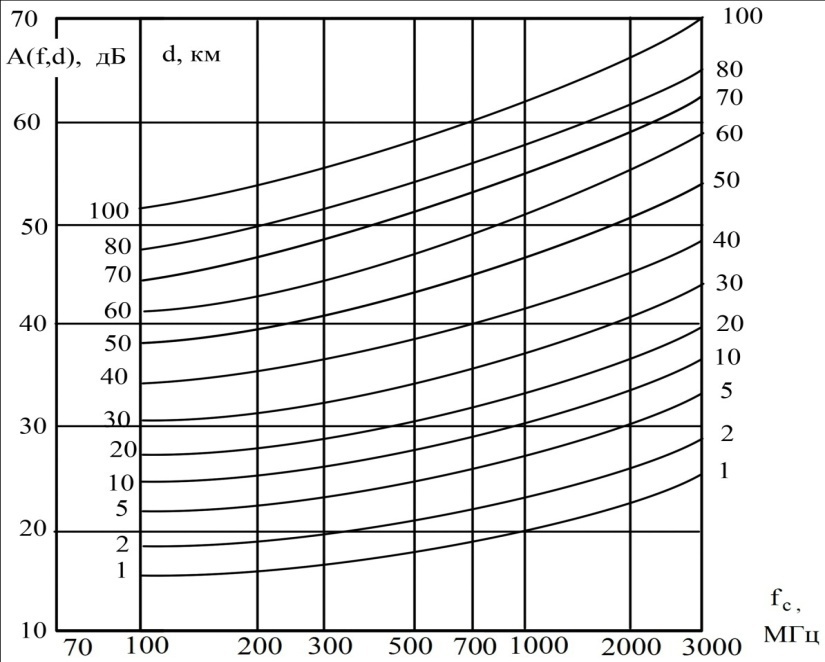 Рисунок 13 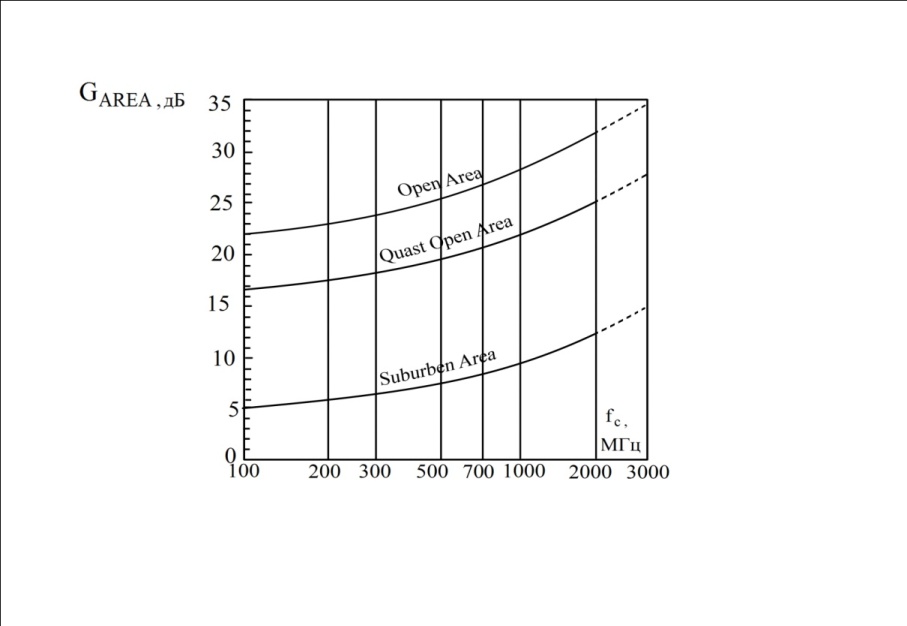 Рисунок 14 - К определению поправочного коэффициента 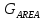 в зависимости от типа местности и несущей частоты в зависимости от типа местности и несущей частотыРисунок 3.13 – Зависимость корректирующего коэффициента эффективной высоты антенны базовой станции в городской местности от растояния 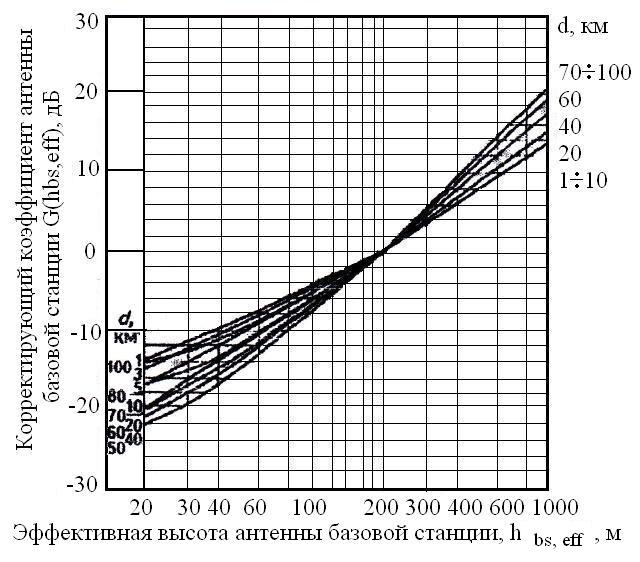 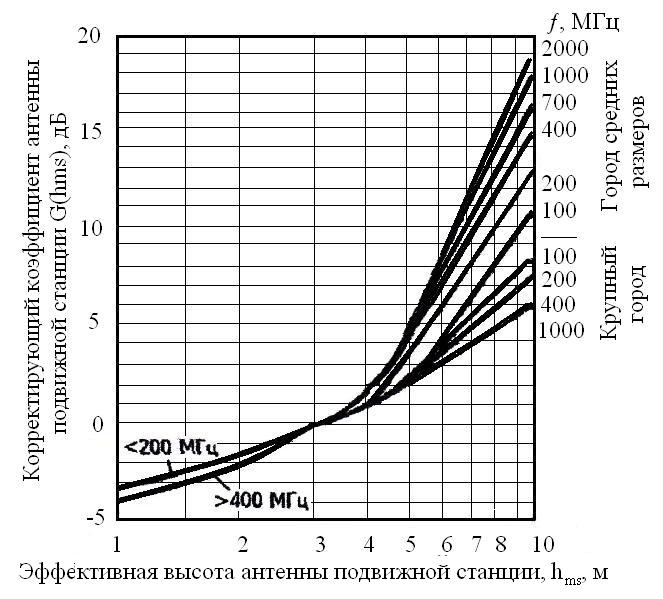 Рисунок 3.14 Зависимость корректирующего коэффициента эффективной высоты антенны подвижной станции от частоты и типа городской застройки В литературе можно обнаружить другой вариант формулы для расчета (L)дБ 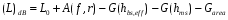 А(f,r) берется как и прежде из графика 13, а корректирующие члены G(hbs,eff) и G(hms) задаются выражениями: 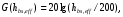  10м < hbs < 1000м 10м < hbs < 1000м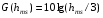 hms ≤ 3м hms ≤ 3м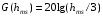 3м < hms < 10 м 3м < hms < 10 мПоправочный коэффициент Garea в дБ зависит от типа местности и несущей частоты и берется из графика на рис. 14. Модель Okamura очень проста. Она основана исключительно на экспериментальных данных, собранных в районе Токио. Характеристики японской городской местности немного отличаются от характеристики местности Европы и США. Но, несмотря, на это, модель пользуется популярностью и считается лучшей для разработки сотовых и других систем наземной подвижной связи [11]. Основной недостаток – медленная реакция на изменение типа местности. Она лучше всего подходит для городских и пригородных районов и не очень эффективна для сельской местности. Уточненные модели в рамках проекта COST #231 ( Cooperation for Scientific and technical Research) Приведенные ранее модели позволяют оценить зависимость потерь от частоты, высот hbs и hms от типа местности. Они неплохо работают на расстоянии, превышающих 1 км и лучше всего подходят для частот до 1,5 ГГц. Однако системы персональной связи (PCS - Personal Communication Systems) работает в диапазоне от 1,8 до 2 ГГц. Примеры таких систем – это DCS 1800 (Digital Communication System, Европа ) и PCS 1900 (Personal Communication System, США) – две версии в системе GSM (Global System Mobile). Поэтому, для создания модели в частотном диапазоне от 1,8 до 2 ГГц в условиях, характерных для систем PCS, были поставлены многочисленные эксперименты и проведены множество измерений. По причине большого затухания сигнала в диапазоне 1,8 ГГц в сравнении с диапазоном 900 МГц, традиционно применяемым в сотовой телефонии, основное различие между PCS и традиционной системой заключается в уменьшении размера сот. Исследования проводились в рамках проекта Европейского Союза COST #231 (Cooperation for Scientific and technical Research). Это уточненные модели COST 231–Hata и Cost 231 - Walfish-Ikegami (Уолфиш-Икегама). |
