ЗВ и мобильная связь 2010. Запорізький національний технічний університет
 Скачать 37.31 Mb. Скачать 37.31 Mb.
|
|
А) диэлектрик 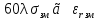 ( почва – диэлектрик). ( почва – диэлектрик).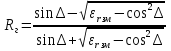 ( ) ( )Из выражения ( ) видно, что коэффициент отражения вещественен. Для всех углов скольжения Δ , 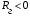 и не превращается в нуль ни при каких значениях Δ вследствие того, что и не превращается в нуль ни при каких значениях Δ вследствие того, что 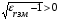 для всех видов почв. Поэтому числитель всегда отрицательный. для всех видов почв. Поэтому числитель всегда отрицательный.Характерные значения 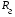 : :Δ=0; 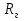 = -1; = -1;Δ=π/2; 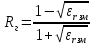 , т.к. , т.к. 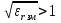 , то , то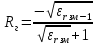 - отрицательный - отрицательныйРавенство 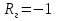 означает, что фаза равна 180о при всех значениях Δ. означает, что фаза равна 180о при всех значениях Δ.График зависимости 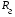 от Δ и фазы изображены на (рис. ). от Δ и фазы изображены на (рис. ).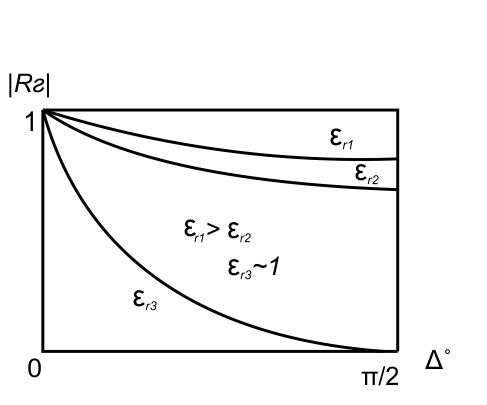 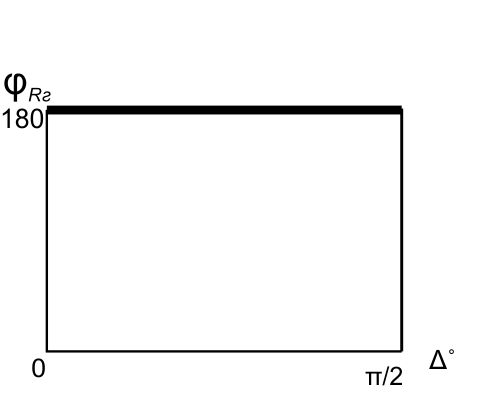 Рисунок 1 Рисунок 2 Рисунок 1- Кривые модуля коэффициента отражения 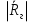 в случае почва-диалектрик для различных в случае почва-диалектрик для различных 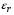 Рисунок 2 - Кривая аргумента коэффициента отражения в случае почва-диэлектрик Характеристика зависимостей 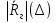 и и 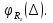 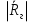 меняется от 1 при Δ= 0 до правильной дроби при Δ= π/2. фаза = 180о всегда одинаковы для всех Δ. меняется от 1 при Δ= 0 до правильной дроби при Δ= π/2. фаза = 180о всегда одинаковы для всех Δ.Б) почва – полупроводник. В этом случае 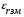 – величина комплексная – величина комплексная 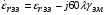 . .И коэффициент отражения будет комплексным 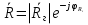 ( ) ( )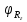 может быть отличен от 0 и 180о. Модуль и фаза может быть отличен от 0 и 180о. Модуль и фаза 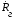 зависит от частоты, так как зависит от частоты, так как 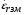 тоже зависит от частоты. тоже зависит от частоты.Графики зависимости 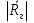 и и 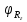 от угла скольжения Δ для этого случая приведены на рисунках (рис. ): от угла скольжения Δ для этого случая приведены на рисунках (рис. ):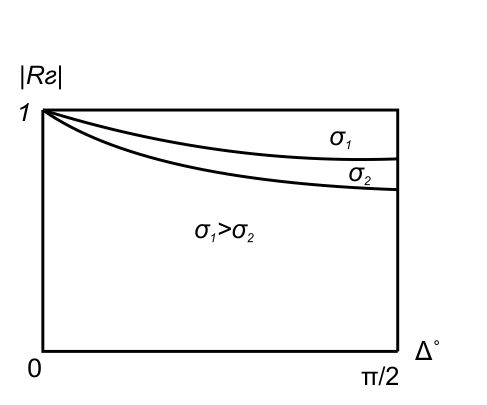 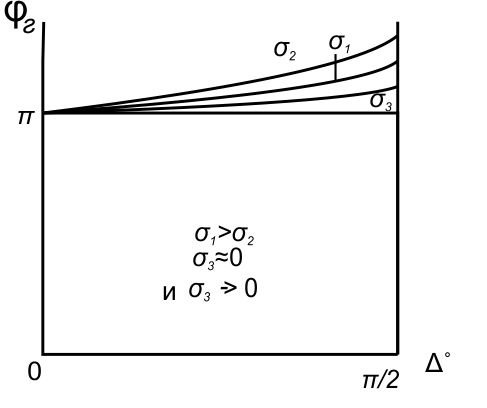 Рисунок Рисунок Рисунок 1- Кривые модуля коэффициента отражения 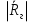 в случае почва-полупроводник для различных значений в случае почва-полупроводник для различных значений 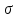 Рисунок 2-Кривые аргумента коэффициента отражения 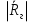 для различных для различных 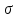 Кривые 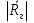 имеют монотонный характер. С увеличением длины волны и электропроводимости почвы модуль имеют монотонный характер. С увеличением длины волны и электропроводимости почвы модуль 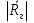 возрастает. Фазы при этом несколько больше и равны 180о. возрастает. Фазы при этом несколько больше и равны 180о.В) почва – проводник. В этом случае при любом угле Δ, происходит полное отражение
( ) Вертикальная поляризация 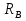 . . При этом виде поляризации коеффициент отражения RВ может быть вычеслен по формуле . ( ) Если 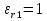 , то , то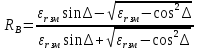 ( ) ( )А) почва – диэлектрик Коэффициент отражения вещественен. 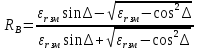 ( ) ( )В этом случае 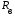 может быть как меньше, так и больше нуля. Действительно, может быть как меньше, так и больше нуля. Действительно,При Δ=0 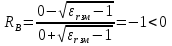 ; ;При Δ=π/2 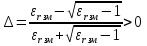 ; ;По этому, при каком то 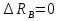 . Этот угол называется углом полного преломления . Этот угол называется углом полного преломления 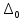 , или углом полного прохождения. , или углом полного прохождения.Приравняв числитель к нулю, получим 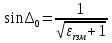 ( ) ( )В этом случае вся электромагнитная энергия при Δ0 проходит в землю, не отражаясь от нее. Графики зависимостей 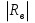 и и 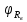 от приведены на рисунках ( ). от приведены на рисунках ( ).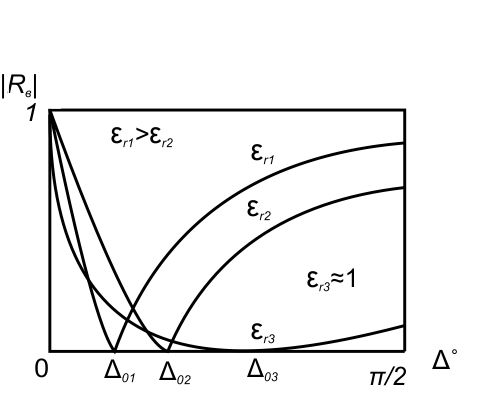 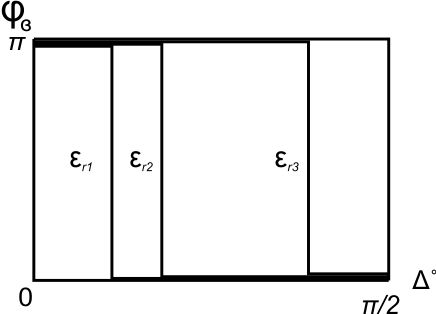 Рисунок Рисунок Рисунок 1- Кривые модуля коэффициента отражения 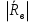 в случае почва-диалектрик для различных значений в случае почва-диалектрик для различных значений 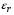 Рисунок 2- Кривые аргумента коэффициента отражения 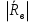 для различных для различных 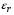 Коэффициент отражения меняется от правильной положительной дроби при 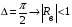 и и 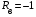 при Δ=0. При при Δ=0. При 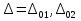 – отражение отсутствует. – отражение отсутствует.Б) почва – полупроводник Коэффициент отражения в этом случае величина комплексная и равна: 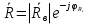 В этом случае характер изменений 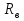 и и 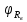 от Δ таков же как в случае диэлектрика, только от Δ таков же как в случае диэлектрика, только 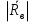 нигде не обращается в нуль, то есть угла полного прохождения нет. Просто существует угол, при котором нигде не обращается в нуль, то есть угла полного прохождения нет. Просто существует угол, при котором 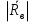 принимает минимальное значение (рис. ). принимает минимальное значение (рис. ).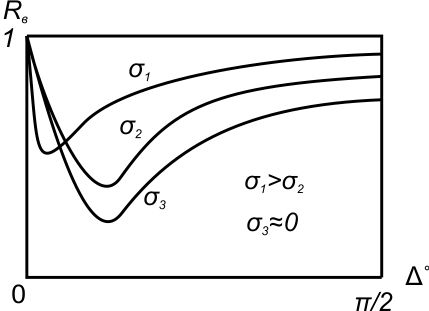 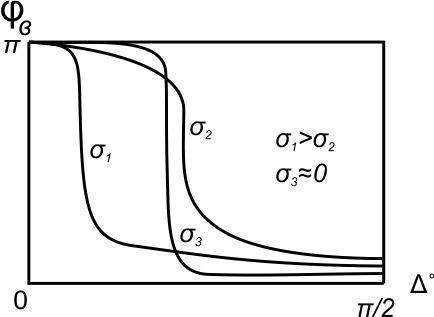 Рисунок Рисунок Рисунок 1 - Кривые модуля коэффициента отражения 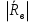 в случае почва-полупроводник для различных значений в случае почва-полупроводник для различных значений 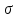 Рисунок 2 -Кривые аргумента коэффициента отражения 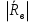 для различных для различных 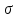 В) почва – проводник для всех углов скольжения
( ) Из ( ) следует, что вся энергия отражается от земли. Для практического определения модуля и фазы коэффициента отражения для двух видов поляризации служат специальные графики зависимости 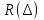 при падении волны на поверхность Земли. [] при падении волны на поверхность Земли. []Сравнение графиков зависимости 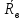 и и 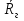 от и от и 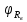 и и 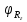 от от 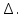 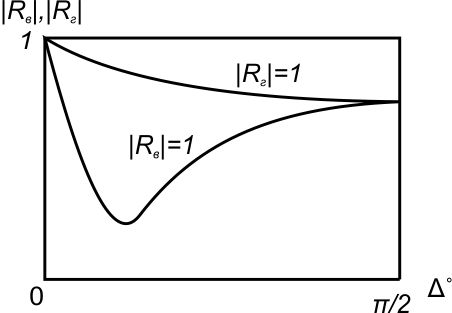 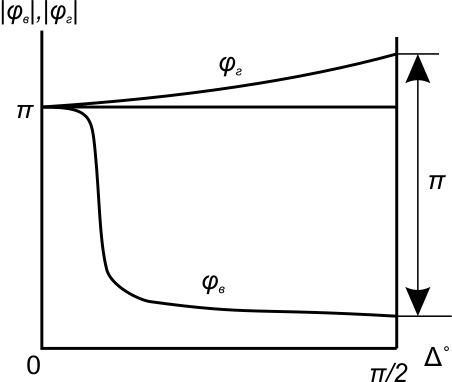 Рисунок Рисунок Рисунок 1- Сравнение модулей коэффициентов отражения Рисунок 2- Сравнения аргументов коэффициентов отражения При углах возвышения Δ=0 и Δ=π/2 модули коэффициентов отражения равны друг другу. При всех других углах 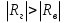 . Это обстоятельство является основной причиной того, что в радиолокации чаще применяют горизонтальную поляризацию. . Это обстоятельство является основной причиной того, что в радиолокации чаще применяют горизонтальную поляризацию.Физические процессы при распространении земной волны. (ЗВ) При распространении земной волны происходят следующие физические процессы:
вторичного поля.
полей, наведенных воображаемыми вторичными источниками в воздухе и почве, которые возбуждаются первичным полем.
Поэтому это сложная дифракционная задача, для определения напряженности поля Е если учесть эти пять процессов. Ее решение было получено ученым Фоком в 1945г. для Земли, считая ее однородным диэлектриком и однородной атмосферой. Классификация методов расчета поля. Решение Фока – это бесконечный ряд, анализ который показывает, что для практических расчетов можно общее решение разделить на несколько частных. Критерием применения служат высота подъема антенн ( h1 , h2) над поверхностью Земли и длина радиолинии( r). С точки зрения высот расположения антенн различают два класса задач:
При решении этих задач необходимо знать область расстояний (зону), где будут беспрепятственно распространяться земные волны. Расстояние прямой видимости rпр. (без учета сферичности земли). Высокоподнятые антенны (I класс) - в этом случае частное решение определяют по соотношению между длиной радиолинии r и предельным расстоянием прямой видимости rпр. Расстояние прямой видимости называется путь по прямой между передающей и приемной антеннами, при котором прямая линия, соединяющая эти антенны, касается земной поверхности в одной точке С. 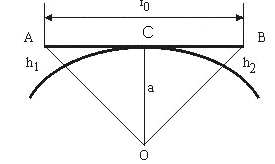 Рисунок - К определению расстояния прямой видимости в случае двух поднятых антенн Величина rпр. отслеживается по дуге большого круга приближенно равна прямой АВ (рис ). В случае однородной атмосферы пункты А и В удалены на расстояние прямой видимости rпр. Так как h1<< aзм , h2<< aзм, то на основании простых геометрических соображений (рис ) имеем. 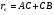 . .Из треугольника ОАС Из треугольника ОСВ 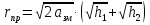 Если выразить 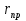 – в км, – в км,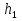 и и 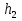 в метрах, то в метрах, то 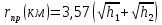 ( ) ( )Модели трасс. В случае поднятых антенн h>>λ принято разбивать трассу линии связи на три участка: зону освещенности, зону полутени, зону тени. Пусть в т.А и т.В находится передатчик и приемник. Для качественного рассмотрения происходящих явлений воспользуемся понятием существенной области при распространении радиоволн. Первая модель - если соотношение между протяженностью трассы и высотами h1 и h2 таково, что первая зона Френеля не достигает выпуклости земной поверхности линия АD (рис. ), то поверхность Земли можно считать плоской и влияние кривизны Земли можно не учитывать. Это дает возможность прямолинейного распространения радиоволн из т.А в т. D. В этом случае протяженность трассы мала по сравнению с расстоянием прямой видимости ( r < 0,2rпр). 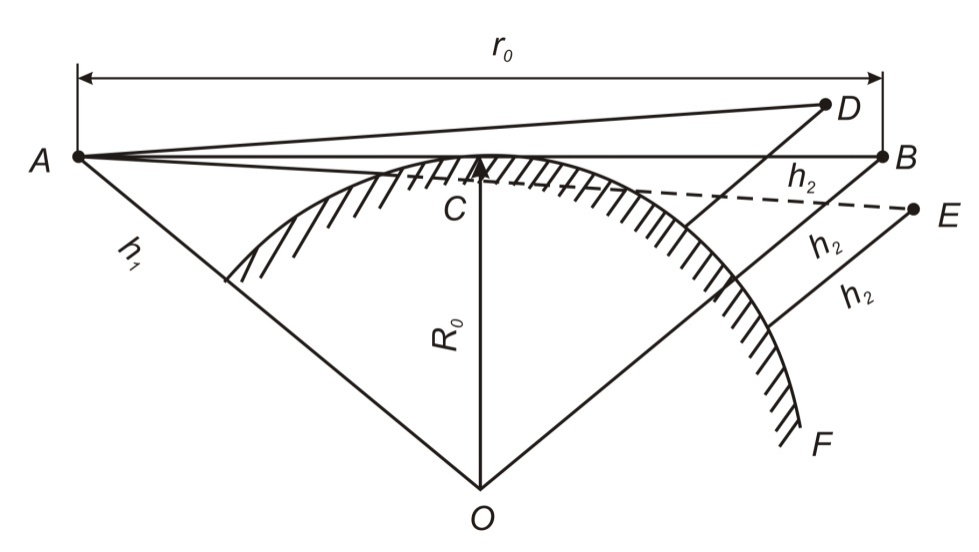 Рисунок – Модель гладкой поверхности Земли Вторая модель если первая зона Френеля не перекрывается выпуклостью земной поверхности, а только ее касается, то необходимо учитывать влияние сферичности Земли. Причем длина трассы (линия АВ) должна находиться в пределах 0,2rпр < r < 0,8rпр. Это область носит название «освещенная область» Третья модель первая зона Френеля охватывает выпуклость Земли (линия АЕ). Это область называется «область полутени». Длина трассы должна находиться в пределах 0,8rпр < r < 1,2rпр . Четвертая модельесли длина трассы r > 1,2rпр ,то область носит название «область тени». В зоне полутени и тени волны распространяются путем дифракции. На рисунке() приведено схематическое изображение рассмотренных моделей. 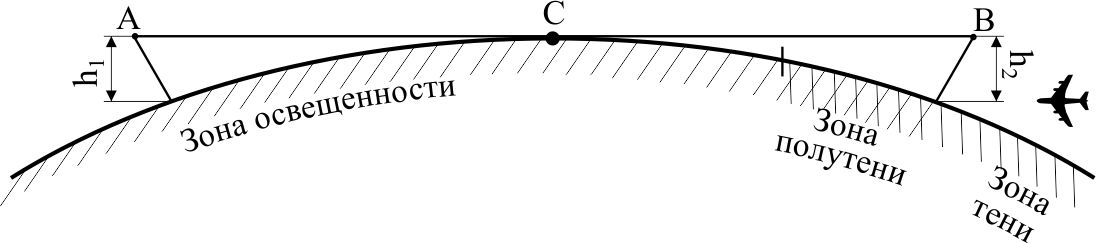 Рисунок - Зоны освещенности, тени и полутени при дифракции радиоволн вокруг земного шара Второе частное решение Фока для низко расположенных антенн(λ >>h). Когда антенны h1 = h2 = 0 (диапазон СВ и ДВ) , понятие расстояния «прямой видимости» не имеет смысла, так как сегмент высотой h ограниченный прямой АВ (рис.) является препятствием для распространения радиоволн. 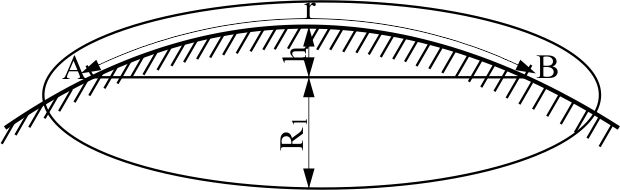 Рисунок – Ко второму частному решению Фока для низко расположенных антенн Пока высота сегмента h не превышает значение максимального R ф1max радиуса первой зоны Френеля 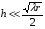 влиянием сферичности земли можно пренебречь, то есть использовать модель плоской земли. влиянием сферичности земли можно пренебречь, то есть использовать модель плоской земли.При низко расположенных антеннах моделью плоской Земли можно пользоваться в метровом диапазоне (10 м - 1 м) для трасс протяженностью 10 – 20 км; в декаметровом диапазоне (100 м – 10 м ) протяженность трассы должна составлять несколько десятков километров, на СВ (1000 м – 100 м) и ДВ (10 км – 1 км) длина трассы должна быть не меньше чем несколько сотен километров. При увеличении r, высота сегмента h станет либо равной, либо больше R ф1max . В этом случае необходимо пользоваться моделью сферической земли, то есть следует учитывать кривизну Земли. . Учет сферичности Земли. Приведенные высоты h1`, h2` ( зоны освещенности 0,2rпр < r < 0,8rпр).Вторая модель Это случай, когда длина линии радиосвязи меньше расстояния прямой видимости. Точка С – точка отражения. В отражательной трактовке поверхность Земли рассматривается как плоскость. Схема распространения радиоволн приведена на рис. 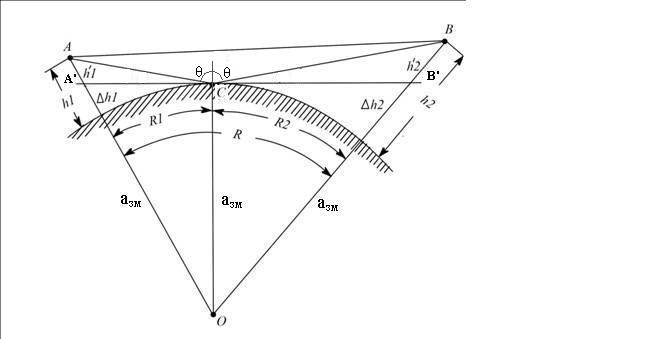 Рисунок К определению «приведенных высот» Если к точке отражения С провести касательную к поверхности земли (прямая A’ и B’) и отсчитывать высоты от этой поверхности, то вводится в рассмотрение вместо истинных высот h1 и h2 так называемые приведенные высоты h1`, h2`. При этом разность хода лучей между прямой и отраженной волной сохраняется и угол падения не изменяется, следовательно, результат будет правильным. В этом случае картина распространения радиоволн над сферической Землей будет аналогично картине распространения над плоской поверхностью. Поле в точке В определяется как результат интерференции прямой волны АВ и волны отраженной от земли (путь АСВ). Если выполнить рисунок с соблюдением масштаба, то было бы видно, что высоты h1 и h1` и h2 и h2’ не имеют углового расхождения и можно считать 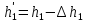 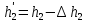 Определим 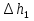 и и 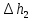 Из Δ OA`C 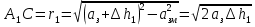 Из Δ OB`C 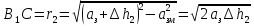 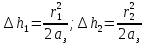 Подставив 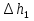 и и 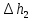 в в 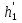 , , 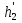 , получим , получим 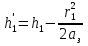 ( ) ( )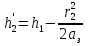 ( ) ( )Полагая aз = 6,73.106 м и выражая r1 и r2 в км получаем удобные для расчета формулы 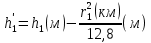 ( ) ( )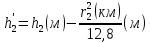 ( ) ( )Полученные формулы показывают, что вычисление приведенных высот упирается в знание местонахождения точки отражения С, или иными словами расстояний r1 и r2. В общем случае определение точки С связано с громоздкими вычислениями. Но вычисления упрощаются для двух простых случаев: для малых расстояний (r ≈ 0,5rпр) и больших расстояний (r ≈ rпр). Для небольших расстояний (r ≈ 0,5rпр) : положение точки определяется по формулам для плоской Земли. 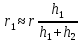 ( ) ( )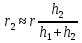 ( ) ( )Для значительных расстояний (r ≈ rпр) прямая AB сливается с ломанной АСВ, то можно считать, что 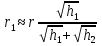 ( ) ( )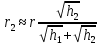 ( ) ( )Для промежуточных случаев положение точки С берут как среднее из двух положений для небольших и больших расстояний. Поле излучателя, поднятого над Землей 1-модель трассы. Интерференционное поле. Интерференционные формулы. На границе раздела воздух – земля происходит отражение волны; напряженность поля отраженной волны определяется при помощи коэффициентов отражения 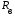 и и 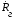 . Поле в точке приема – результат интерференции полей прямой волны (путь АВ) и отраженной (АСВ). . Поле в точке приема – результат интерференции полей прямой волны (путь АВ) и отраженной (АСВ).Введем обозначения : r – длина линии связи; h1, h2 – высоты передающей и приемной антенны. Считаем, что выполняется условие h1>>λ, h2>>λ, что практически возможно на УКВ, иногда на КВ. При небольшой протяженности трассы, считаем землю плоской. Поместим в точке А элементарный вибратор (диполь), например, вертикальный вибратор – простейший источник сферических волн. Им может быть и горизонтальный вибратор (рис. ). Поэтому задачу на отражение сферической волны от плоской границы воздух – земля можно рассматривать таким образом: электромагнитное поле создается электрическим или магнитным диполем, помещенным в первую среду (εa1, μa1, σ1). Необходимо определить влияние на это поле второй среды (почва с εa2, μa2, σ2). Задача решается строго методом разделения переменных, но с упрощением, считается, что вторая среда – идеально проводящая, а затем с учетом отражения плоской волны от плоской границы раздела распространяют это решение на среду с конечными электромагнитными параметрами. При решении используется еще метод зеркальных изображений (МЗИ): замена влияния на переменное электромагнитное поле идеально отражающей поверхности влиянием зеркально расположенного источника. Суть метода состоит в следующем 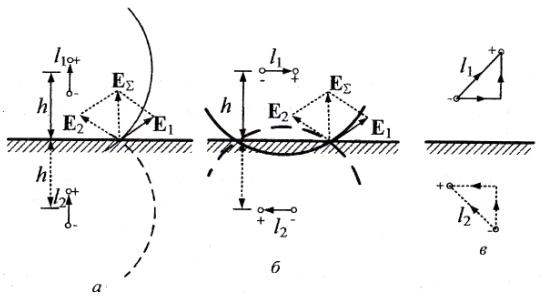 Рисунок К методу зеркальных изображений Путь отраженной волны по ломанной АСВ можно заменить равным ему путем А’СВ, если, считать, что источником отраженной волны является вибратор, находящийся под поверхностью земли на расстоянии h1 и влиянием Земли заменить влияние второго вибратора (МЗИ) – так называемый виртуальный источник. 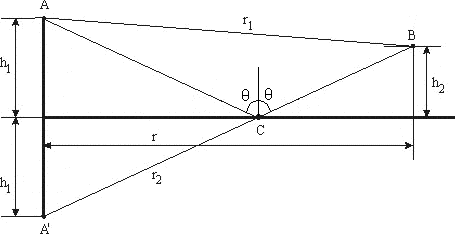 Рисунок - Схема распространения радиоволн в случае, когда передающая и приемная антенны поднятии над поверхностью земли Напряженность электромагнитного поля в точке А (напряженность поля прямой волны АВ) 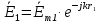 Поле отраженной волны 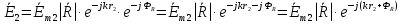 где 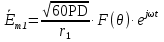 , ,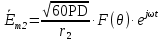 , ,- комплексные амплитуды напряженностей электромагнитного поля прямой и отраженной волны в свободном пространстве; 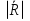 – коэффициент отражения от земли; – коэффициент отражения от земли;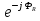 – фаза коэффициента отражения. – фаза коэффициента отражения. Исходя из условия, что r>>h1 и r>>h2, прямые проведенные из т. А и А` можно считать параллельными в точке приема В. 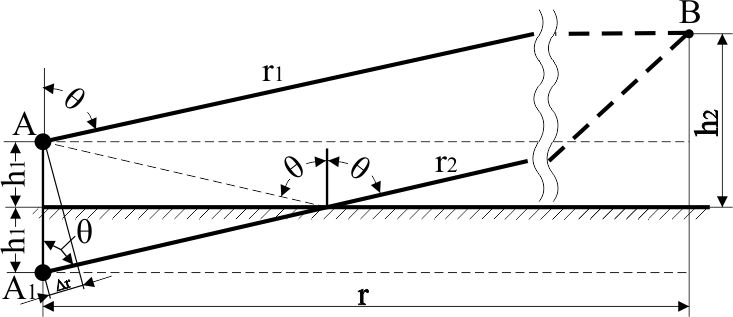 Рисунок - Определение разности расстояний, пройденных прямой и отраженной волнами Из рисунка ( ) можно легко определить разность расстояний r1 и r2 через высоту передающей антенны h1 и угол падения θ на поверхность 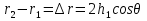 ( ) ( )Оценим влияние 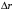 на амплитуду и фазу результирующей напряженности электромагнитного поля ( ) в т. В. на амплитуду и фазу результирующей напряженности электромагнитного поля ( ) в т. В.Амплитуда Разность 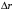 величина небольшая, поэтому при вычислении ее влиянием можно пренебречь и считать, что амплитудные значения прямой и отраженной волны приблизительно равны величина небольшая, поэтому при вычислении ее влиянием можно пренебречь и считать, что амплитудные значения прямой и отраженной волны приблизительно равны 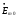 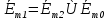 ( ) ( )Фаза При нахождении фазы такое допущение делать нельзя, влияние 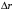 необходимо учитывать. Используя выражения ( ) и ( ) можно записать необходимо учитывать. Используя выражения ( ) и ( ) можно записать  Откуда 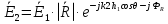 ( ) ( )Результирующее поле в т.В запишется в комплексной форме 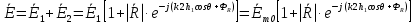 В тригонометрическом виде это выражение имеет вид 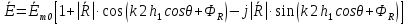 Вычисляя модуль, имеем 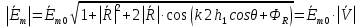 , ( ) , ( )где 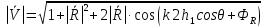 , ( ) , ( )где в ( ) Еm0 – поле в свободном пространстве; а в ( ) V – множитель ослабления, учитывающий влияние Земли. Формула носит название интерференционной для 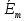 . .Рассмотрим частные случаи ее применения. Напряженность электрического поля в зоне тени Для решения задачи распространения земной волны в близи полупроводниковой сферы необходимо решить волновое уровнение сферической системы координат. Для значительных расстояний в области тени, когда сферичность земли экранирует точку приема , можно использовать только первый член ряда В.А.Фока из общего выражения для напряженности электрического поля в точке приема. При этом напряженность поля можно определить по этой формуле 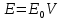 где, 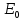 - это напряженность поля в свободном пространстве; а - это напряженность поля в свободном пространстве; а 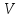 - множитель ослабления. - множитель ослабления.Множитель ослабления является результатом произведения трех функций 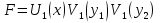 или в децибелах 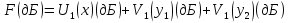 где 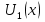 - это функция, которая зависит от расстояния и электрических параметров земли; - это функция, которая зависит от расстояния и электрических параметров земли; 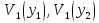 - это функции, которые зависят от высоты размещения передающей и приемной антенн. Параметры - это функции, которые зависят от высоты размещения передающей и приемной антенн. Параметры 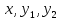 определяются по формулам определяются по формулам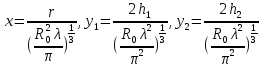 Для определения функций 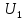 и и 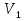 по параметрам по параметрам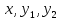 существуют графики приведенные на рисунке ( ). существуют графики приведенные на рисунке ( ).Если антенны размещены в близи Земли, то для определения напряженности поля в зоне дифракции служат графики Международного консультативного комитета с радиосвязи ( МККР), построенные на основании расчетов за дифракционными формулами( рис ). На графиках приведена зависимость напряженности поля от расстояния при мощности передатчика 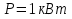 и и 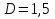 для разных длин волн и разных электрических параметров земной поверхности рис(7.24-7.25) . Что бы определить напряженность поля при заданной мощности излучения необходимо значения напряженности поля умножить на величину для разных длин волн и разных электрических параметров земной поверхности рис(7.24-7.25) . Что бы определить напряженность поля при заданной мощности излучения необходимо значения напряженности поля умножить на величину 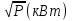 . Напряженность поля в зоне дифракции уменьшается с расстоянием значительно быстрее нежели при распространения радиоволн над плоской земной поверхностью. Поэтому напряженность поля в зоне дифракции значительно ослаблена. . Напряженность поля в зоне дифракции уменьшается с расстоянием значительно быстрее нежели при распространения радиоволн над плоской земной поверхностью. Поэтому напряженность поля в зоне дифракции значительно ослаблена.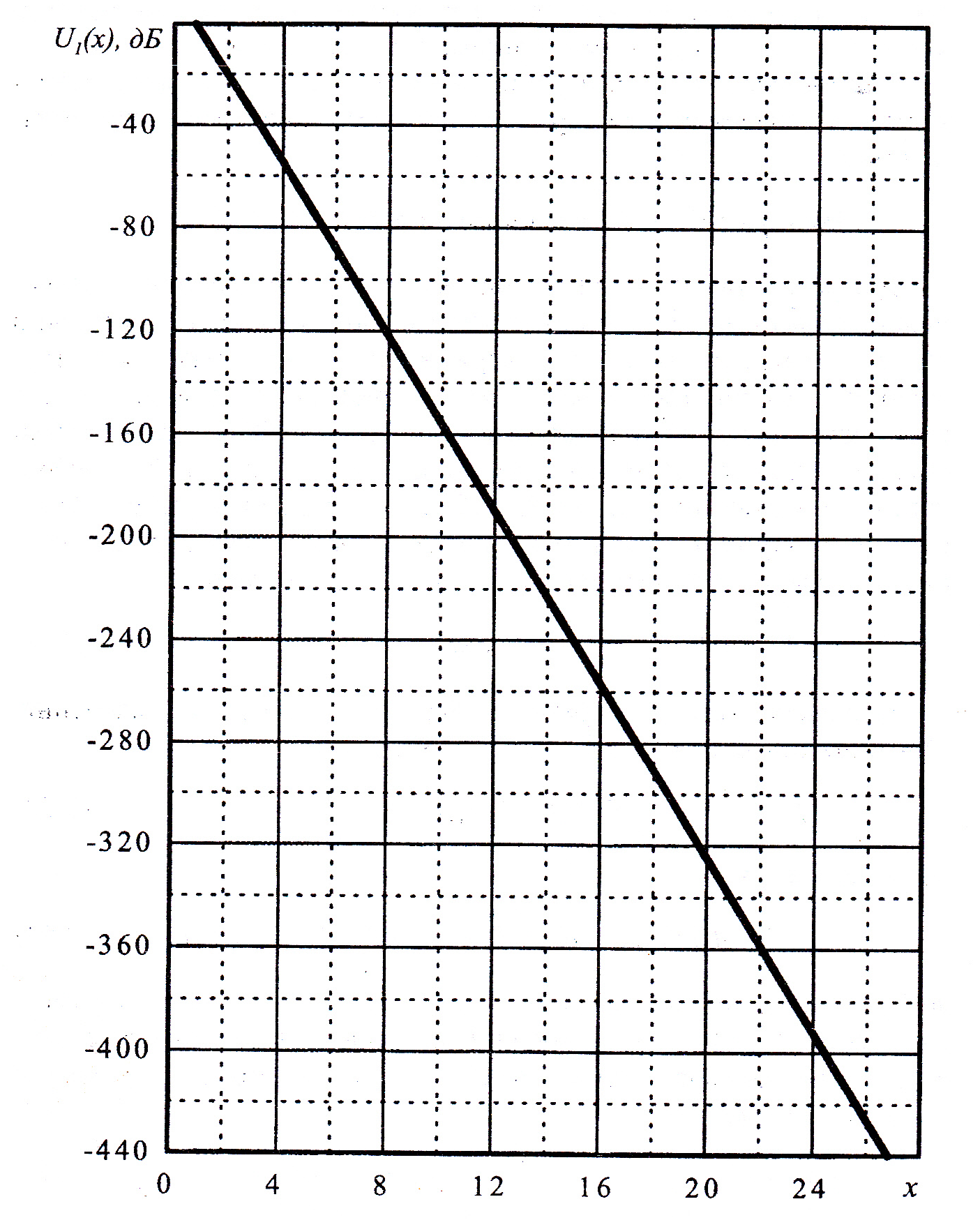 Рисунок – Зависимость 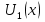 в децибелах относительно расстояния в децибелах относительно расстояния 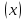 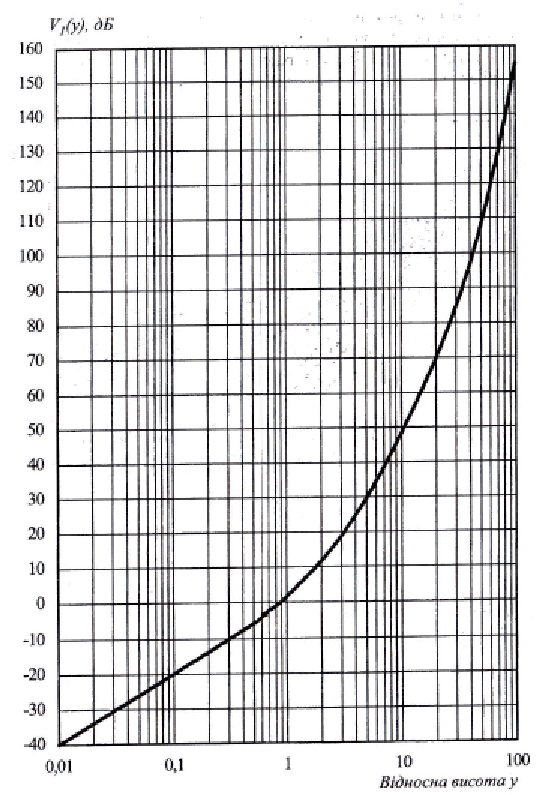 Рисунок – Зависимость высотного множителя 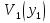 в децибелах от относительной высоты антенны в децибелах от относительной высоты антенны 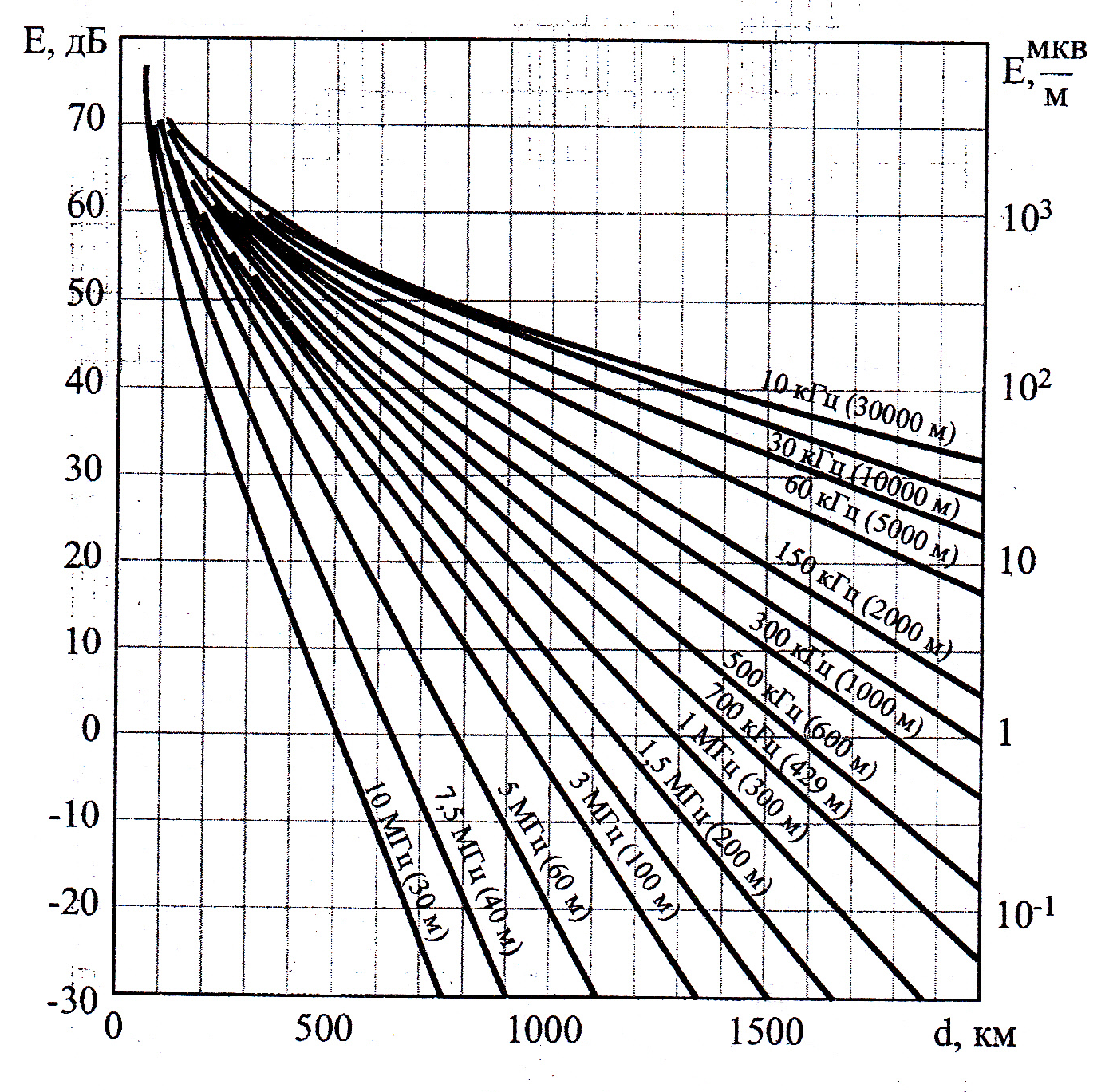 Рисунок – Зависимость поля земной волны от расстояния при распространении над морем; 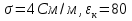 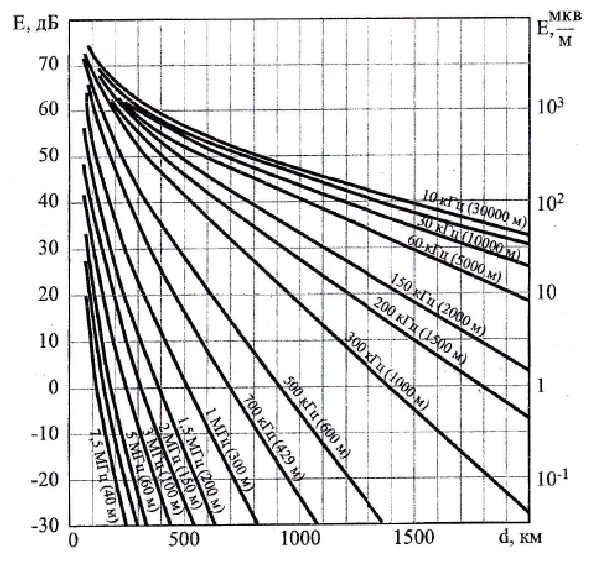 Рисунок – Зависимость поля земной волны от расстояния при распространении над сушей; 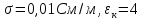 Вертикальный диполь Если вертикальный диполь – излучатель, то нужно учитывать его диаграмму направленности 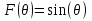 . .Следовательно, для этого случая результирующее вертикально поляризованное поле запишется: 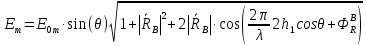 (* ) (* )В ( ) амплитуда изменяется в зависимости от угла падения θ не только вследствие направленности излучения диполя ( 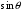 ), но и от изменения множителя ослабления V. ), но и от изменения множителя ослабления V.Вертикальный вибратор создает вертикально поляризованную волну, поэтому следует пользоваться значениями модуля и фазы коэффициента отражения для вертикальной поляризации( 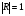 , ,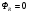 ) )Входящий в ( ) множитель 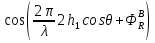 указывает на существование интерференционных максимумов и минимумов. Количество максимумов зависит от отношения указывает на существование интерференционных максимумов и минимумов. Количество максимумов зависит от отношения 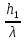 . .
которых: 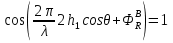 А это возможно если аргументы принимают значения 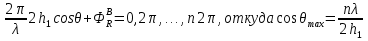 Так как в случае вертикальной поляризации фаза коэффициента отражения 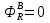 (идеально проводящая Земля). То выражение ( *) запишется : (идеально проводящая Земля). То выражение ( *) запишется :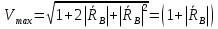 () () |

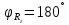
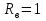 а,
а, 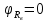
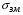 .
.