ЗВ и мобильная связь 2010. Запорізький національний технічний університет
 Скачать 37.31 Mb. Скачать 37.31 Mb.
|
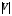 недопустимы и необходимо пользоваться дифракционными формулами[]. недопустимы и необходимо пользоваться дифракционными формулами[]. Поле низко расположенного электрического вибратора в зоне приближения плоской земли В диапазонах сверхдлинных волн (декаметровых, гектометровых) и более длинных волн излучение и приём проходит в условиях, когда высоты поднятия антенн h1 и h2 < λ. При таком расположении антенн работа радиосистем осуществляется на дифракционной волне, скользящей вдоль поверхности Земли. Исследование структуры поля скользящей волны в зоне приближения плоской Земли ведут при следующих допущениях:
Введем прямоугольную систему координат, ось X совпадает с направлением распространения, а ось Z направлена по вертикале вверх. Составляющие напряженности электромагнитного поля в верхней среде (воздух) обозначим индексом 1 (E1, E1Z, П1,Н1У, E1Х), а составляющие во второй среде (в полупроводящей) с индексом 2 (E2, E2Z, П2,Н2У, E2Х). Рассмотрим более простой случай, когда излучатель расположен вблизи идеально проводящей поверхности. К этому случаю близко распространение волн ДВ диапазона под морем. Тогда проводимость идеально проводящей поверхности 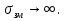 Энергия, излученная таким вибратором распространяется только в верхнем полупространстве над плоскостью и напряженность поля по сравнению со свободным пространством увеличивается в два раза. ДН имеет максимум излучения вдоль земли при вертикально поляризации и отсутствует при горизонтальной. Согласно граничным условиям[] вектор напряженности электрического поля направлен перпендикулярно к поверхности, а вектор Пойнтинга параллельно поверхности (рис .а). При распространении над идеально проводящей поверхностью структура поля не изменяется, т.к. утечка в Землю отсутствует. 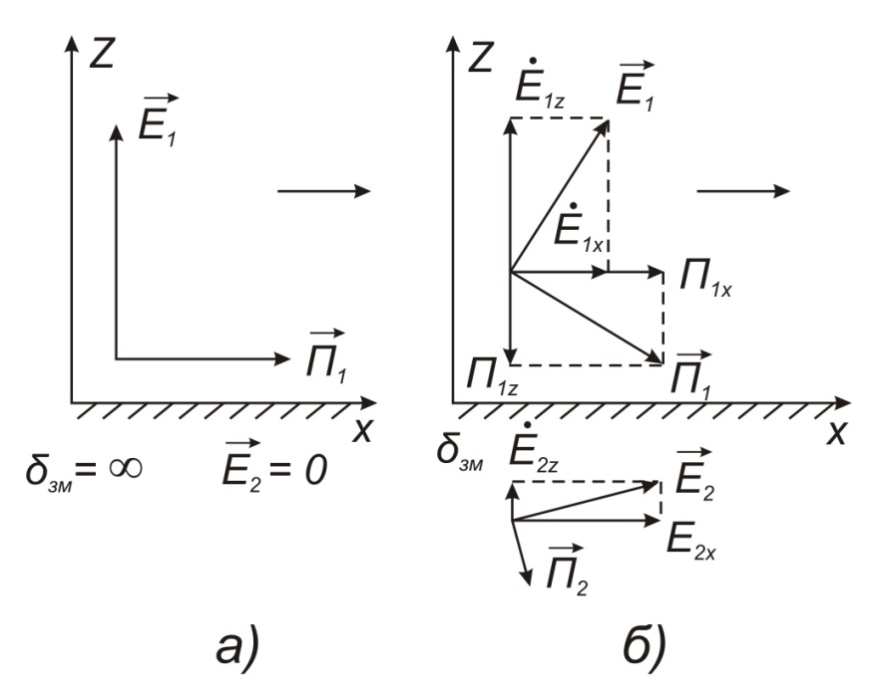 Рисунок - Структура поля низко расположенного вертикального вибратора в зоне плоской Земли: а) 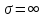 ; б) ; б)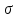 - конечная - конечная Если поверхность неидеальный проводник, то 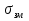 имеет конечное значение, а имеет конечное значение, а 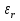 будет величиной комплексной: будет величиной комплексной: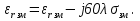
( ) Структура поля в воздухе у поверхности земли В процессе распространения над Землёй с конечной проводимостью σзм часть энергии утекает в Землю, проникая в глубь земной поверхности. Следовательно, помимо составляющей вектора Пойнтинга П1х, направленной вдоль к поверхности земли, имеется составляющая П1Z, направленная перпендикулярно к поверхности Земли. Суммарный вектор П1 оказывается наклонённым под некоторым углом к земной поверхности, а это значит, что вектор Е1 отклоняется от первоначального направления (σзм = ∞). Таким образом, над поверхностью Земли с конечной проводимостью всегда имеются две составляющие электрического поля Е1х и Е1z (рис. ). Определим соотношение между ними. Если считать, что известна вертикальная составляющая Е1z, то в случае плоской волны в воздухе горизонтальная составляющая магнитного поля будет равна  () ()Эта составляющая Н1у связана с горизонтальной составляющей Е1х приближёнными граничными условиями Щукина-Леонтовича, которые относительно земли являются касательными . Составляющие Е1х и Н1у связаны соотношением 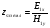 , а , а 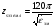 , отсюда , отсюда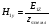 . ( ) . ( )Приравняв ( ) и ( ), получим  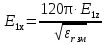 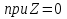 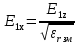 () ()Используя ( ) для 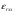 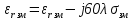 , и подставив его в формулу (2) в виде модуля и фазы, получим , и подставив его в формулу (2) в виде модуля и фазы, получим 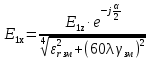 , () , ()Из формулы () видно, что вертикальная составляющая поля над поверхностью Земли всегда больше горизонтальной. Чем больше λ и σ, тем меньше будет горизонтальная составляющая. 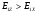 в воздухе. в воздухе.В диапазоне СВ и низких частот (НЧ) (10км-1км) при обычных значениях проводимости почвы E1Zmax и E1Хmax отличаются в десятки и сотни раз. Предельным случаем является морская поверхность, которая на очень низких частотах близка по своим свойствам к проводнику 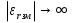 , а E1Хmax → 0. , а E1Хmax → 0.Во всех случаях излучение и приём земной волны в непосредственной близости Земли выгодно вести на вертикальной поляризации. Из соотношения () видно, что результирующее поле над поверхностью земли оказывается поляризованным эллиптически, то есть волна перестает быть плоской. Ортогональные составляющие E1Z и E1Х сдвинуты на угол 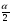 , т.е. результирующий вектор Е1 описывает эллипс. Но т.к. E1Z >> E1Х, то эллипс поляризации сильно вытянут. Поэтому приближённо считают, что в воздухе на поверхности Земли поле линейно поляризовано. Результирующий вектор ориентирован в направлении большой оси эллипса, т.е. наклонён под углом вперёд на угол ψ, относительно нормали, который согласно (3) равен , т.е. результирующий вектор Е1 описывает эллипс. Но т.к. E1Z >> E1Х, то эллипс поляризации сильно вытянут. Поэтому приближённо считают, что в воздухе на поверхности Земли поле линейно поляризовано. Результирующий вектор ориентирован в направлении большой оси эллипса, т.е. наклонён под углом вперёд на угол ψ, относительно нормали, который согласно (3) равен 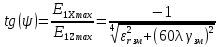 () ()Угол ψ называется «углом наклона фронта волны» (рис.) 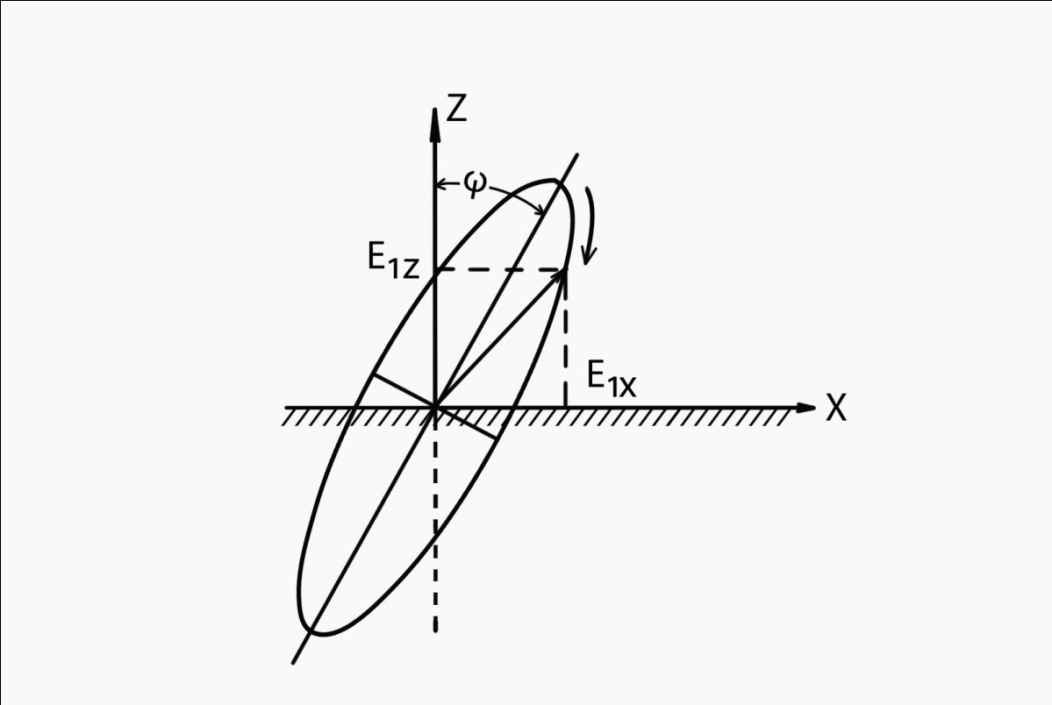 Рисунок - Эллипс поляризации волны, распространяющейся вдоль плоской поверхности Земли Структура поля в почве у границы раздела Структура поля в почве у границы раздела воздух-почва определяется из таких точных граничных условий:
Тогда 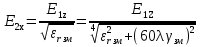 () ()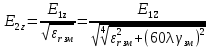 () ()Н1У = Н2У = 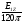 ; ; Из выражений () и () и граничного условия Е2Х = Е1Х, следует, что горизонтальная составляющая в почве (в морской воде) больше вертикальной составляющей Е2Х max >> Е1Z max т.к. подкоренные выражения много больше единицы. По этому необходимо применять здесь антенны с горизонтальной поляризацией. Расчёт напряжённости поля низкорасположенных антенн (h1, h2 << λ) Напряжённость поля земной волны, скользящей вдоль поверхности можно определить волновым методом путём решения уравнений Максвелла с учётом граничных условий на границе раздела воздух-почва. Решение представляет собой сложную задачу даже для случая плоской поверхности раздела. Впервые решение предложил в 1909 г. А. Зоммерфельд в интегральной форме, которая непригодна для инженерных расчётов. В 1923-1926 годах при некоторых допущениях эта задача была решена Шулейкиным и голландским ученым Ван-дер-Полем, которая даёт возможность определить вертикальную составляющую земной волны, при расположении излучателя на плоской поверхности раздела воздух-почва. Известно, что напряжённость электрического поля при распространении волны над полупроводящей поверхностью, меньше, чем на идеально проводящей поверхностью, вследствие проникновения энергии радиоволн в полупроводящую Землю, где частично теряется в ней (рис. ). 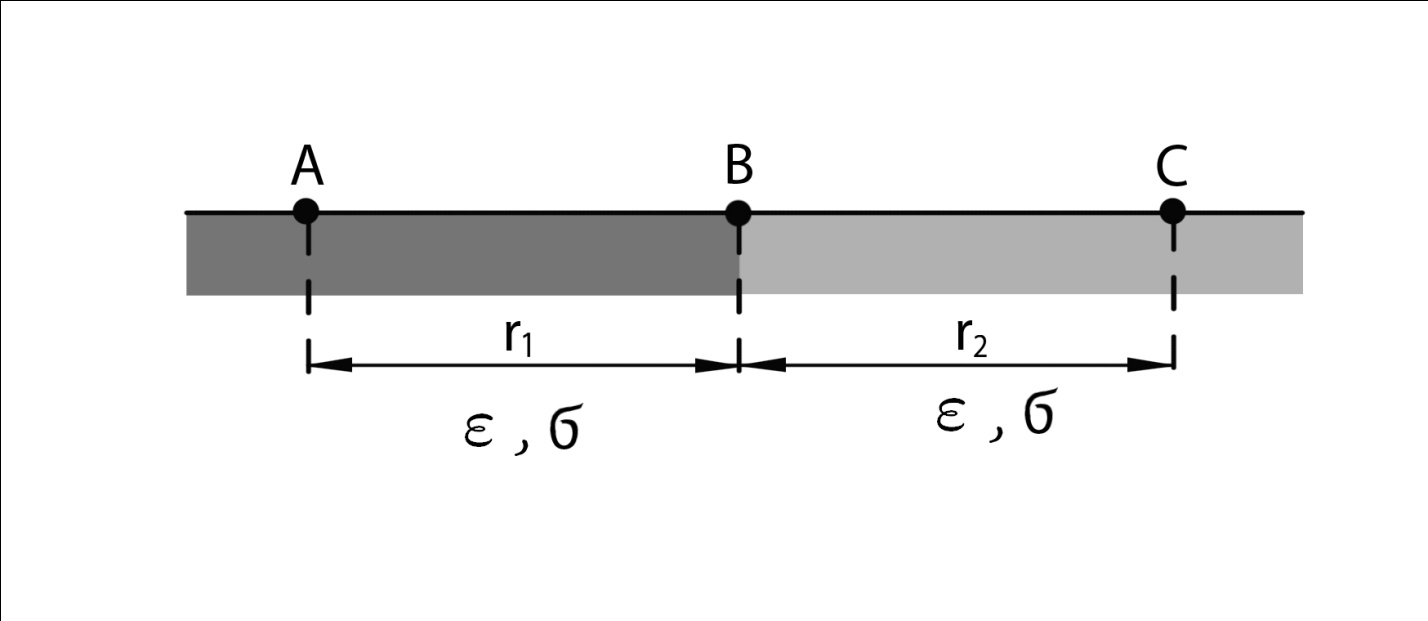 Рисунок Это уменьшение оценивается коэффициентом ослабления 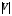 . .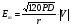 . .В общем случае величина 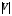 - величина комплексная и является сложной функцией от некоторого комплексного безразмерного аргумента ρ, который называется численным расстоянием. Он зависит от длины волны, электрических свойств почвы, протяжённости трассы. - величина комплексная и является сложной функцией от некоторого комплексного безразмерного аргумента ρ, который называется численным расстоянием. Он зависит от длины волны, электрических свойств почвы, протяжённости трассы. 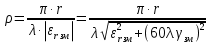 , ,где 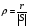 - отношение действительного расстояния к так называемому масштабу расстояния - отношение действительного расстояния к так называемому масштабу расстояния 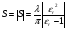 , [м] который в общем случае величина комплексная. , [м] который в общем случае величина комплексная. 1) Для волн диапазона СВ и более низких обычно, 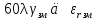 , то есть токи проводимости больше токов смещения то численное расстояние равно: , то есть токи проводимости больше токов смещения то численное расстояние равно: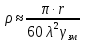 ( ) ( )2) Для другого крайнего случая, когда токи смещения превышают токи проводимости: 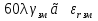 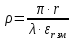 ( ) ( )Если ρ известно, то расчёт поля сводится к вычислению функции V(ρ). Такой расчёт проводится методом численного интегрирования. Но эти громоздкие вычисления заменяют определением V(ρ) по графикам, составленными Берроузом в логарифмическом масштабе (рис. ). На практике с достаточной степенью точности можно вести расчёт по приближённой формуле, которая аппроксимирует кривую на рисунках – для двух видов поляризации для различных 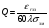 . .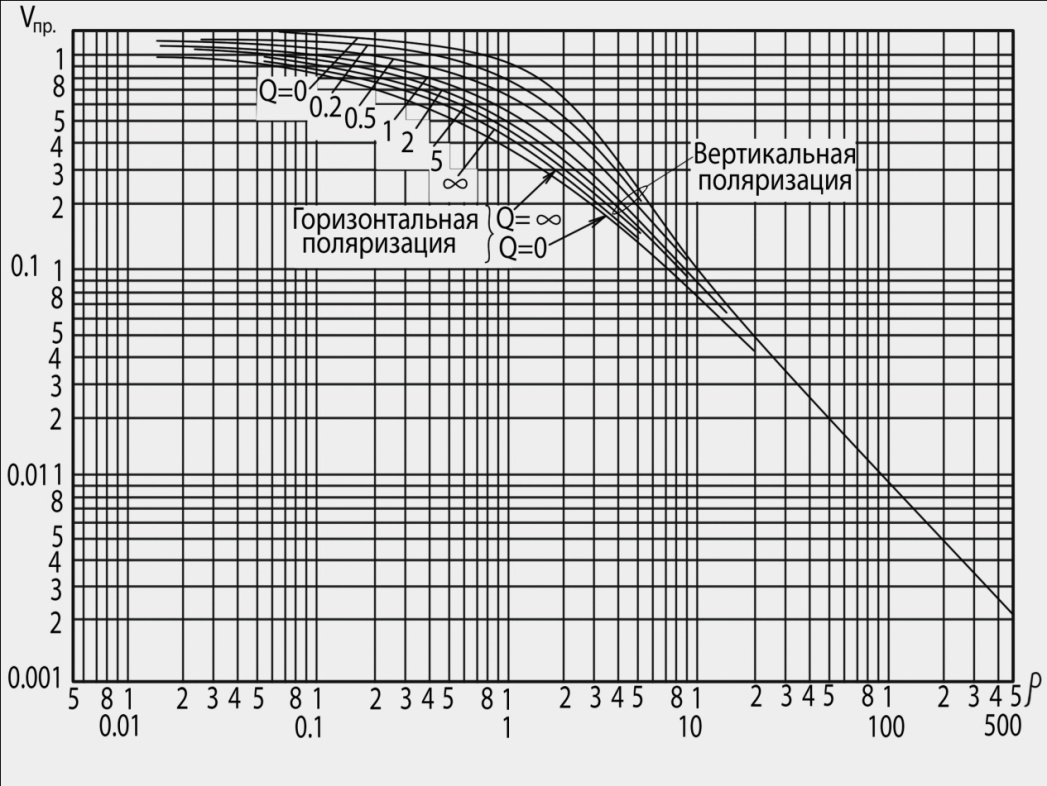 Рисунок – Зависимость множителя ослабления от численного расстояния 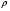 при разных значениях параметра Q при разных значениях параметра QПри отсутствии графика показанного на этом рисунке ( ) модуль множества ослабления можно вычислить по приближенной формуле 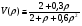 ( ) ( )Ею можно пользоваться при небольших удалениях от передатчика ( 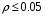 ). В этом случае можно пренебречь кривизной земли. Из формулы ( ) видно что при небольших значениях ). В этом случае можно пренебречь кривизной земли. Из формулы ( ) видно что при небольших значениях 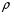 множитель ослабления слабо зависит от множитель ослабления слабо зависит от 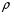 и близок к единице. т.е. слабо уменьшается с изменением расстояния, длины волны и электрических свойств почвы. Напряженность электрического поля меняется по закону и близок к единице. т.е. слабо уменьшается с изменением расстояния, длины волны и электрических свойств почвы. Напряженность электрического поля меняется по закону 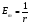 как в свободном пространстве. Эта формула получила название Шулейкина–Ван дер Поля. как в свободном пространстве. Эта формула получила название Шулейкина–Ван дер Поля. При ρ > 25 величина 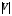 изменяется обратно пропорционально ρ, причём изменяется обратно пропорционально ρ, причём 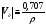 или или  ( ) ( )Напряжённость поля изменяется по сложному закону, а не по экспоненте, как в поглощающей среде. Формулами Шулейкина можно пользоваться только на расстояниях 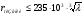 , где λ - [м], r – [км]. Причём ошибка не превышает 10 %. При не выполнении этого условия нельзя пользоваться из-за сферичности Земли. , где λ - [м], r – [км]. Причём ошибка не превышает 10 %. При не выполнении этого условия нельзя пользоваться из-за сферичности Земли. Распространение радиоволн над неоднородной почвой. Взлётные и посадочные площадки. Явление береговой рефракции Теория и практика показывают, что при использовании антенн, расположенных вблизи поверхности земли, наибольшее влияние не распространение радиоволн оказывают участки земной поверхности, находящиеся в непосредственной близости от передающей и приёмной антенн. Формулы для расчёта напряжённости электрического поля над неоднородной трассой учитывают самые простые случаи – трассы, состоящие из 2-х или 3-х однородных участков, границы между которыми резко выражены, например, при переходе трассы с суши на море. Схематически это будет выглядеть следующим образом в приближении плоской земли (рис. ). 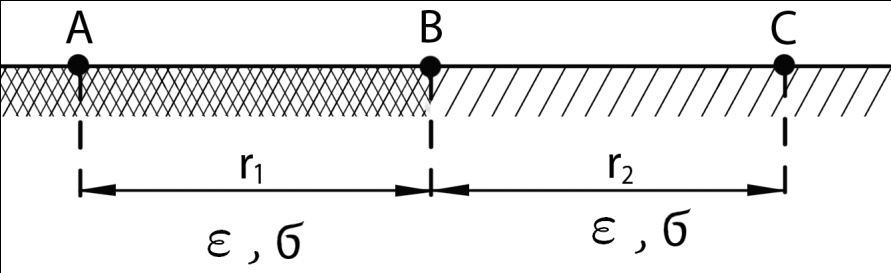 Рисунок - Распространения земных радиоволн над неоднородной трассой (последовательно над двумя почвами) Необходимо определить множитель ослабления в т.В. Строгие решения выполнены советскими учёными, а именно Фейнбергом, дали формулы для расчёта коэффициента ослабления 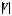 , при распространении радиоволн над неоднородной поверхностью, над трассой, состоящей из двух и трёх участков: , при распространении радиоволн над неоднородной поверхностью, над трассой, состоящей из двух и трёх участков:
Трасса, состоящая из двух разнородных участков. Множитель ослабления равен: 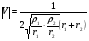 , ( ) , ( )где 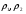 - численные расстояния двух участков, - численные расстояния двух участков, 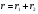 - полная длина трассы. - полная длина трассы.При этом должны выполняться неравенства 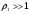 , , 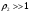 Из выражения для 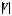 видно, что оно симметрично относительно параметров видно, что оно симметрично относительно параметров 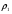 и и  , т.е. оба участка поверхности прилегающих к передающей и приёмной антеннам являются одинаково важными для распространения радиоволн над неоднородной трассой. , т.е. оба участка поверхности прилегающих к передающей и приёмной антеннам являются одинаково важными для распространения радиоволн над неоднородной трассой.Графики зависимости напряжённости электрического поля над трассой, состоящей из двух участков «суша-море» и «море-суша» приведены на рис. 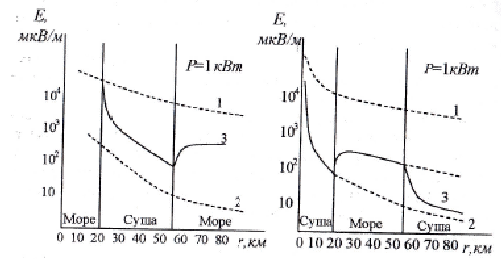 Рисунок – Зависимости изменения напряженности электрического поля от расстояния которое состоит из трех участков Проанализируем эти зависимости:
В случае однородной трассы: однородная морская трасса; однородная сухопутная трасса - с увеличением расстояния r, напряжённость электрического поля всегда убывает, причём Еморск > Есухоп. В случае неоднородной трассы «суша-море» наблюдается явление повышения уровня поля при пересечении береговой линии (переход на участки с более высокими значениями σ).
В этом случае, когда передатчик на море, а приёмник на суше, переход от моря к суше сопровождается существенным уменьшением напряжённости поля. Трассы, состоящей из трёх участков 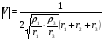 , ( ) , ( )где 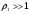 , , 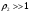 , , 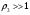 . . 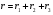 - полная длина трассы, причём - полная длина трассы, причём 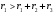 Графики зависимостей напряжённости электрического поля для трёх участков приведены на рисунке (). Из рисунка видно, что напряжённость поля в точках приёма всегда будет больше, если концевые участки трассы обладают большей проводимостью по сравнению со средним. Из формулы для 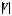 видно, что напряжённость поля не зависит от электрических параметров среднего участка. видно, что напряжённость поля не зависит от электрических параметров среднего участка. «суша-море-суша» - напряжённость близка напряжённости поля на однородной сухопутной трассе. «море-суша-море» - напряжённость близка напряжённости поля над однородной морской трассе. Ещё нагляднее влияние концевых участков трассы видно из графика зависимости 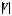 от коэффициента заполнения трассы сушей от коэффициента заполнения трассы сушей 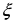 . . Коэффициент заполнения трассы сушей называется отношение протяжённости трассы, проходящей над сушей к протяжённости всей трассы. 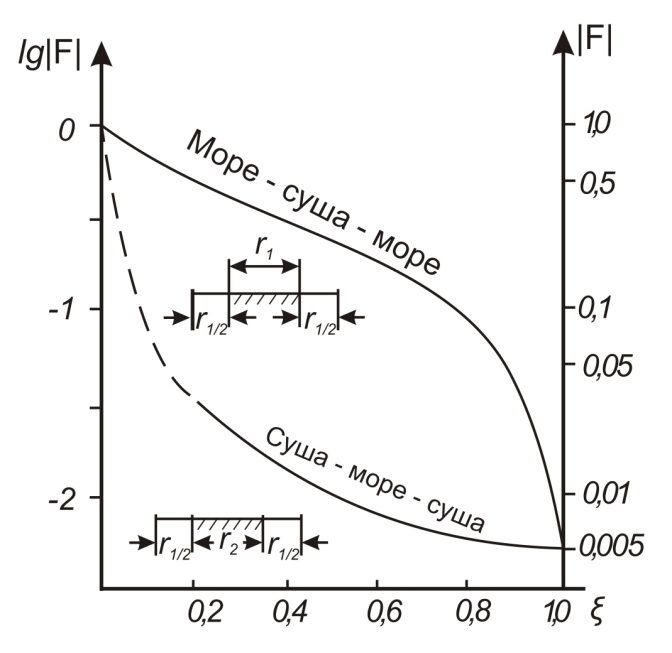 Рисунок - Функция ослабления при распространении радиоволн над трассами «суша-море-суша» и «море-суша-море» в зависимости от степени заполнения трассы сушей 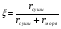 Из рисунка () видно, что если трасса имеет концевые участки состоящие из суши («суша-море-суша»), даже при малой протяженности этих участков ( 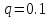 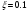 ),множитель ослабления резко убывает. ),множитель ослабления резко убывает.Если концевые участки море («море-суша-море») влияние суши сказывается только при 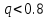 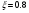 , при этом кривая резко падает и приближается к кривой «суша-море-суша». , при этом кривая резко падает и приближается к кривой «суша-море-суша».Взлётные и посадочные площадки При распространении земных волн вносимое отдельным участком поглощение зависит от местоположения участка на трассе. Наибольшее поглощение оказывают участки, непосредственно примыкающие к передающей и приёмным антеннам, которые называются «взлётной» и «посадочной» площадками. Ввёл название академик Л.И. Мандельштам. Это необычное поведение земных волн можно объяснить следующим образом. Рассмотрим два случая:
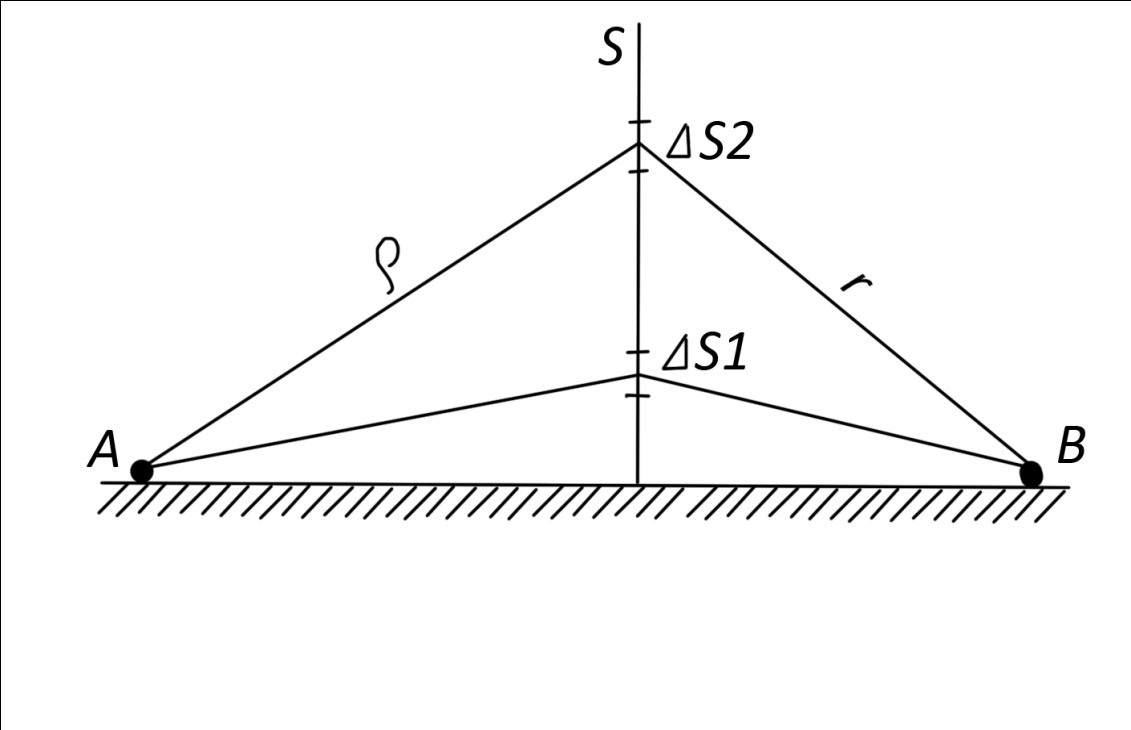 Рисунок – К понятию взлетных и посадочных площадок Земля - плоская и идеально проводящая. Согласно принципу Гюйгенса-Френеля в точке В (рис. ) формируется поле за счёт суммирования полей вторичных источников, расположенных, например, на плоскости S, перпендикулярной к поверхности земли, причём в т. В напряжённость равна 2Есв.пр.. Площадки ΔS1, ΔS2 расположены на разных высотах и вклад будет определяться расположением 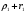 , , 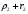 и т.д. Причём у ΔS1 и т.д. Причём у ΔS1 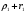 меньше, чем ΔS2 меньше, чем ΔS2 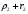 . Чем меньше расстояние, тем больший вклад. Следовательно ΔS1 даёт самый большой вклад в суммарную напряженность поля. . Чем меньше расстояние, тем больший вклад. Следовательно ΔS1 даёт самый большой вклад в суммарную напряженность поля. Земля-полупроводник. Картина меняется. Ослабляющее действие Земли действует сильнее на ΔS1, чем на ΔS2. На ΔS2 почти не сказывается влияние земли, т.е. вклад вносят участки, расположенные на некоторой высоте от поверхности Земли. 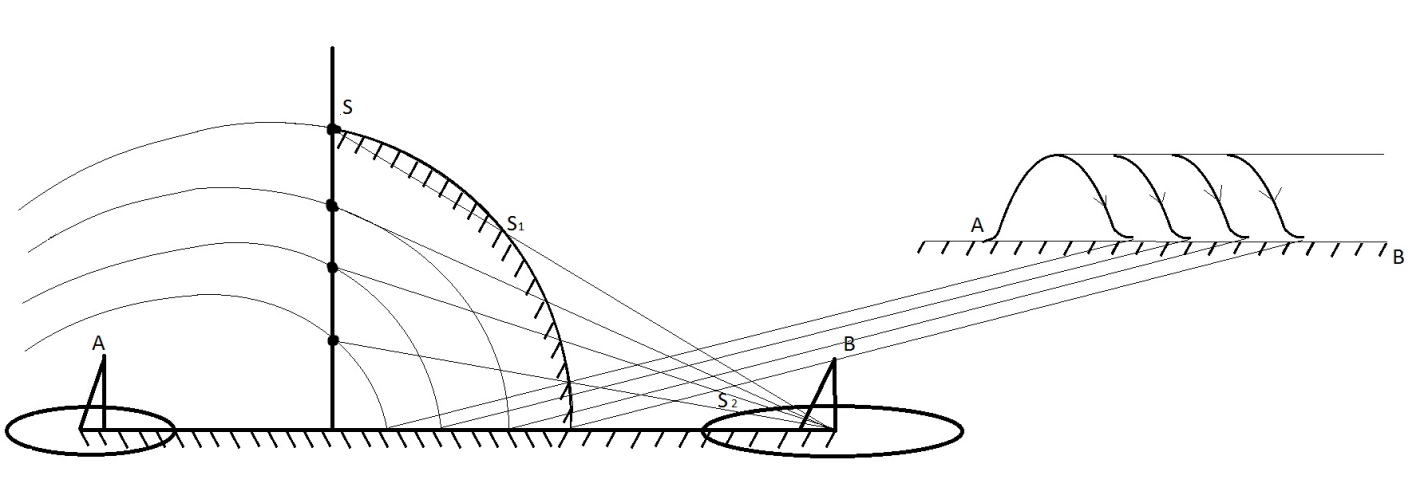 Рисунок Поле в т. приема согласно принципу Г-Ф создается элементарными источниками на поверхности S1 , проходящий воздух, и элементарными источниками, наведенными волной на поверхности S2 . Существенную роль играют только те источники на поверхности Земли, которые расположены вблизи приемной антенны. Токи, неведение в Земле являются вторичными источниками и будут тем больше, чем выше проводимость поверхности. Чем выше проводимость «посадочной площадки», тем больше ЭДС наводится в приемной антенне, расположенной над этой площадкой. Токи на участках Земли вдали от приемной антенны мало влияют на ЭДС. Особая роль «взлетной» площадки : она находится вблизи передающей антенн, где велика объемная плотность энергии, излученной передатчиком. Если проводимость плохая, то значительная доля общего количества энергии передатчика поглотиться Землей. Это уменьшит интенсивность источников Гюйгенса на S1 и S2 , которые создают поле вблизи приемной антенн. Вдали от передатчика энергия «размазана» по большему объему, основной запас энергии сосредоточен в пространстве над Землей. Потери энергии в Земле на этом участке трассы уменьшают интенсивность источников Гюйгенса только небольшой части поверхности S1 принимающей и Земли. Поле в точке приема создается на всей поверхности S1 и уменьшение интенсивности источников небольшой части поверхности мало влияют на ЭДС в приемной антенне. Поэтому антенны поля передающих и приемных центров таких линий желательно распологать в районах с высокой проводимостью почвы. Подобный способ может служить для осуществления радиосвязи между двумя погруженными лодками – это условный пример, ибо она осуществляется другими методами (рис. ). 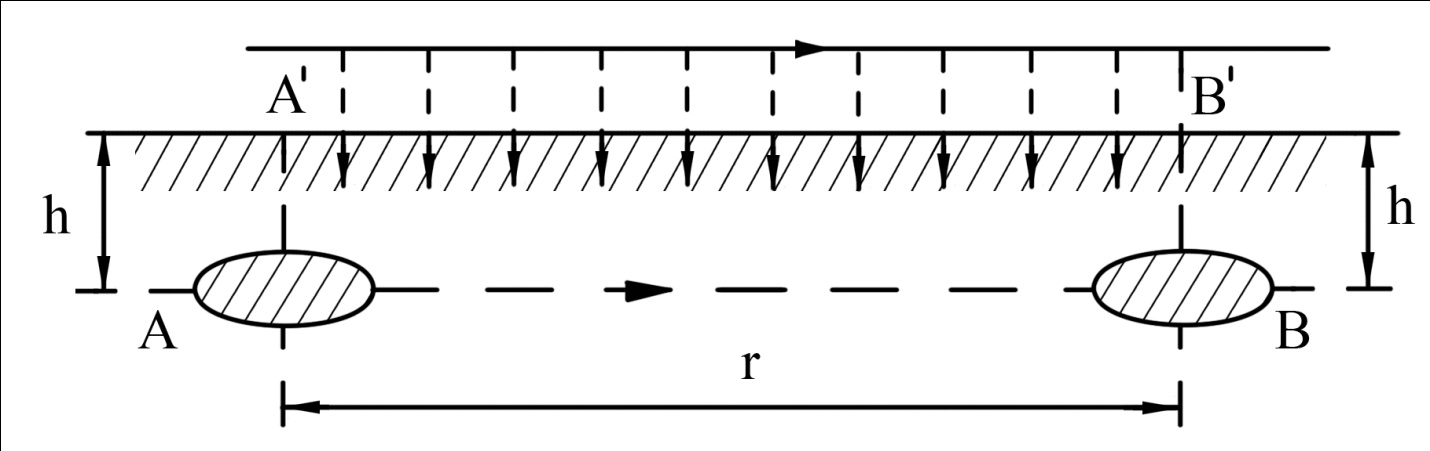 Рисунок - К определению понятий «взлетной» и «посадочной» площадок На рис.( ) r>>h – глубина погружения. При распространении в морской воде радиоволн сильно поглощается, поэтому волны по пути r создают ничтожное поле в точке В. Более сильное поле создаётся волной вышедшей на поверхность моря в т. А’ и распространяется как земная волна вдоль поверхности раздела, дойдя до т. В' и затем углубляется в море на отрезок h достигнув второй подлодки в т. В. Путь АА’В’В похож на путь «взлётных» и «посадочных» площадок. Береговая рефракция При распространении радиоволн над неоднородной трассой, в зависимости от соотношения между длинами однородных участков меняется не только модуль множителя ослабления, но и его фаза. Это вызывает изменение ориентации фазового фронта, т.е. направления распространения волны, или береговую рефракцию. Суть явления береговой рефракции состоит в следующем. Предположим, что корабельный передатчик находится в т. А на море на большом расстоянии от берега. А радиопеленгатор – на суше в т. В вблизи береговой линии (рис. ). В отсутствии рефракции точки C, В, D находились бы на эквифазной поверхности, или линии. Эта линия – представляла бы собой дугу окружности радиусом r с центром в месте расположения излучателя. Приведем нормаль к этой поверхности 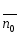 Когда радиоволны пересекают береговую линию, то симметрия относительно т. А нарушается и эквифазная поверхность займёт положение, которое показано пунктирной линией (NBM). Нормаль 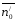 к эквифазной линии в этом случае показывает действительное направление волн в месте расположения пеленгатора. Угол Δφ между векторами к эквифазной линии в этом случае показывает действительное направление волн в месте расположения пеленгатора. Угол Δφ между векторами 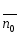 и и 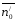 представляет ошибку пеленгования, обусловленную береговой рефракцией. Имеются специальные графики и номограммы для расчёта этих углов [].Ошибка пеленга наблюдается при малых численных расстояниях (ρ<<1). представляет ошибку пеленгования, обусловленную береговой рефракцией. Имеются специальные графики и номограммы для расчёта этих углов [].Ошибка пеленга наблюдается при малых численных расстояниях (ρ<<1).Ошибка пеленга уменьшается при увеличении σпочвы и удалении точки В от берега. При значительных численных расстояниях ρ>>1 ошибка пеленга практически исчезает, в силу, что фазовая скорость практически не отличается от скорости света. Отклонение пеленга от истинного значения обычно не превосходит 3-5 0. 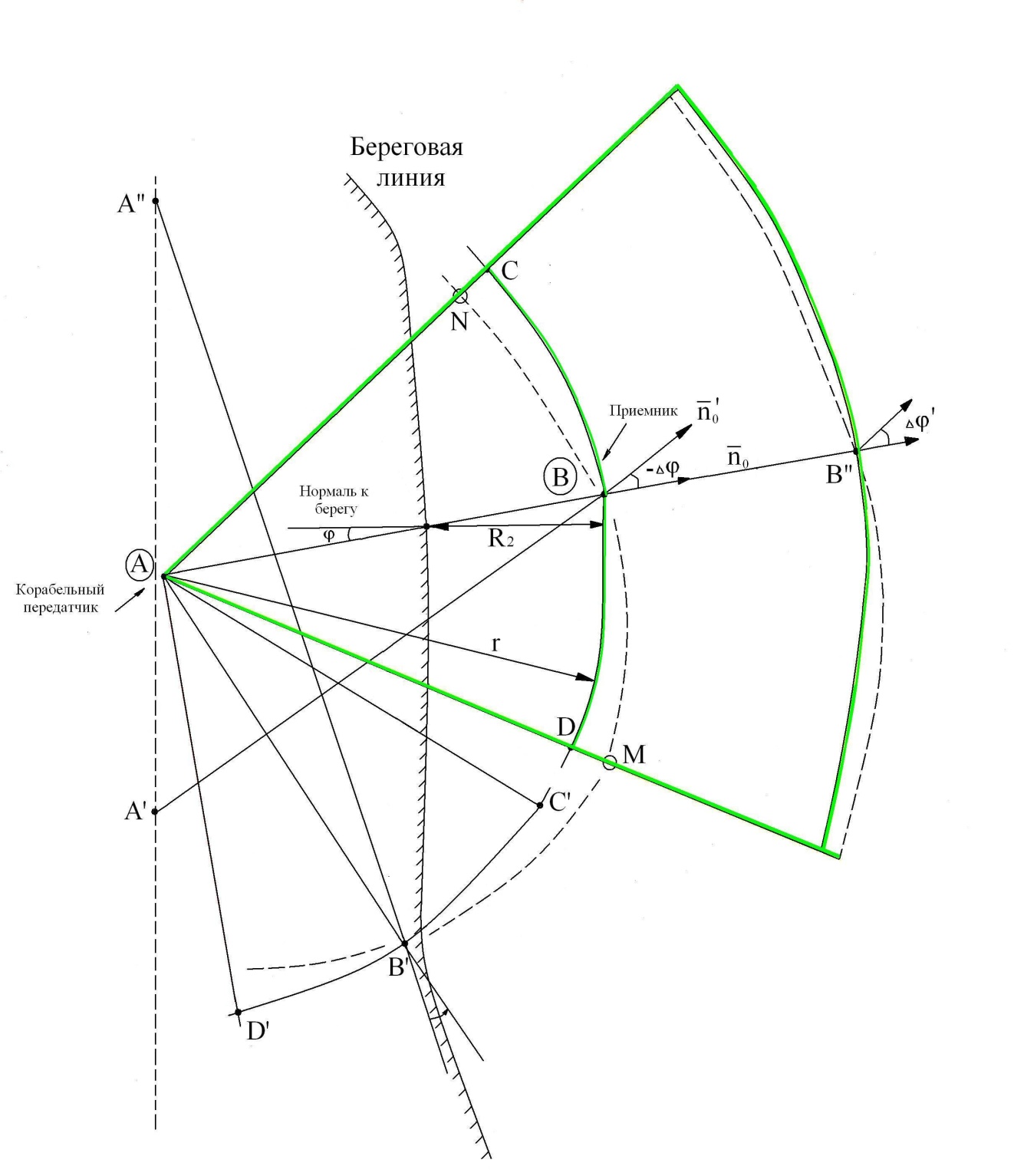 Рисунок – К пояснению явления береговой рефракции Расчет ошибки пеленга Если считать морской участок трассы идеально проводящим и предположить, что точка передачи А расположена настолько далеко от береговой линии, что падающую волну можно считать плоской, то угол рефракции Δφ при малых углах падения, можно рассчитать по формуле 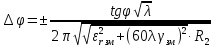 , (рад) ( ) , (рад) ( )где R2 – расстояние от точки приёма до береговой линии по нормали к ней; φ – угол падения; Знак («+») соответствует расположению точки приёма на море; Знак («-») – расположение этой точки на суше. Формула ( ) пригодна для расчета Δφ если 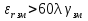 . .Из формулы видно, что | Δφ | тем больше, чем больше φ – угол падения и убывает по мере удаления от береговой линии.
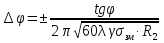 , рад., ( ) , рад., ( )т.е. не зависит от длины волны. В обычных условиях Δφ не превышает несколько градусов. Распространение радиоволн при наличии на пути экранирующих препятствий На закрытых трассах, проходящих в горных районах, напряженность поля УКВ определяется особенностями горного рельефа, из которых основными являются большая изрезанность рельефа местности и наличие препятствий в виде отдельных гор или ряда горных хребтов. Форма препятствий может быть самой разнообразной: от остроконечных гор большой высоты, до пологих холмов сравнительно малой высоты. Для определения поля в точке приёма на таком виде трассы применяют хорошо разработанные в физической оптике методы расчёта дифракционного поля, главным образом принципом Гюйгенса-Френеля. Электрические параметры препятствия не учитываются, либо считают, что они «непрозрачны». При этом горный хребет аппроксимируется одиночным клиновидным препятствием. Возможно два случая распространения радиоволн при наличии клиновидного препятствия (абсолютно поглощающий экран).
 Рисунок - Распространение радиоволн при наличии на пути клиновидного экрана (H > 0) 2) Экран пересекает путь АВ. Высота Н в этом случае – отрицательный знак. (H < 0, это область тени). 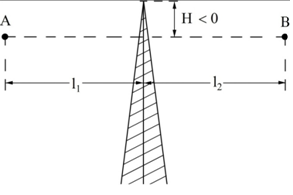 Рисунок - Распространение радиоволн при наличии на пути клиновидного экрана (H < 0) Г.С. Ландсберг в книге «Оптика» [ ] показал, что множитель ослабления по отношению к свободному пространству можно вычислить по формуле 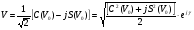 , (* ) , (* )где 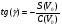 ; ; 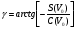 , , 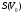 и и 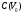 - интегралы Френеля: - интегралы Френеля: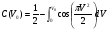 - интегральный косинус - интегральный косинус 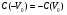 , , 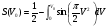 - интегральный синус - интегральный синус 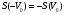 . .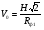 - параметр дифракции, а - параметр дифракции, а 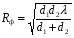 - радиус первой зоны Френеля. - радиус первой зоны Френеля. Графики функций 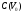 и и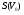 приведены на рис ( ). приведены на рис ( ). 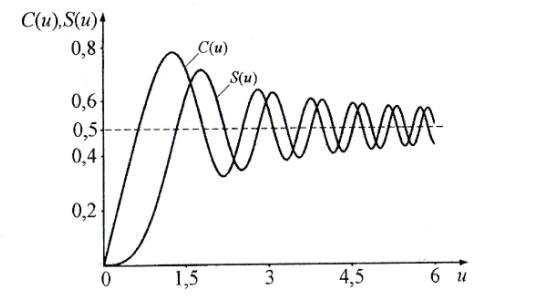 Рисунок - графики функций 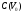 и и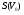 Физические представления: 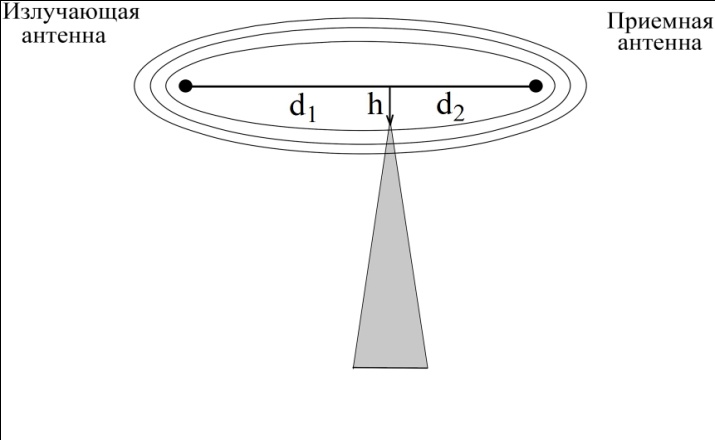 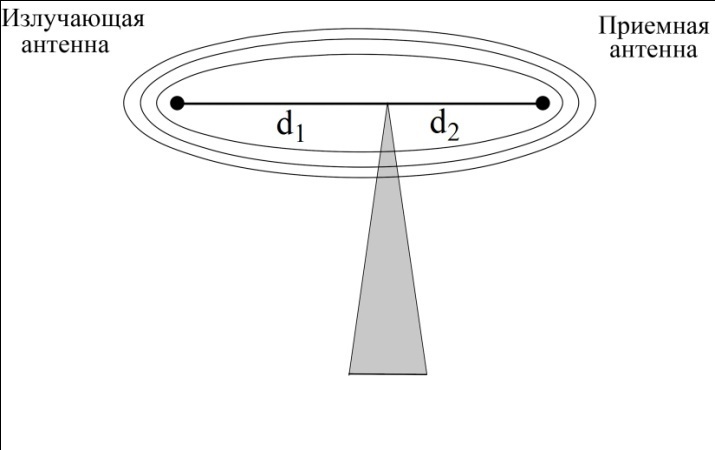 а) Н> Rф1 б) H=0 Рисунок - Варианты перекрытия видимости антенн препятствием Экран загораживает различные участки кольцеобразных зон Френеля, которые можно построить в плоскости перпендикулярной линии АВ, которая проходит через плоскость экрана, как это делалось, при изучении зон Френеля. В зависимости от H, d1 и d2 меняется соотношение между площадью закрытых экраном и свободных участков зон Френеля, что вызывает изменение множителя ослабления. От величины просвета Н зависит количество зон Френеля, участвующих в создании поля в точке приёма. Если просвет несколько велик, что уменьшается в 8-12 первых зон Френеля, то напряжённость поля в точке приёма не отличается от Е в свободном пространстве (рис.а,б). Если препятствие пересекает первую зону Френеля, то множитель ослабления уже не будет равен единице, как в свободном пространстве. Качественная картина влияния препятствия стоящего на пути распространения радиоволн приведена на рис. (зависимость модуля коэффициента от параметра дифракции) и на рис.( график распределения фазы множителя ослабления). 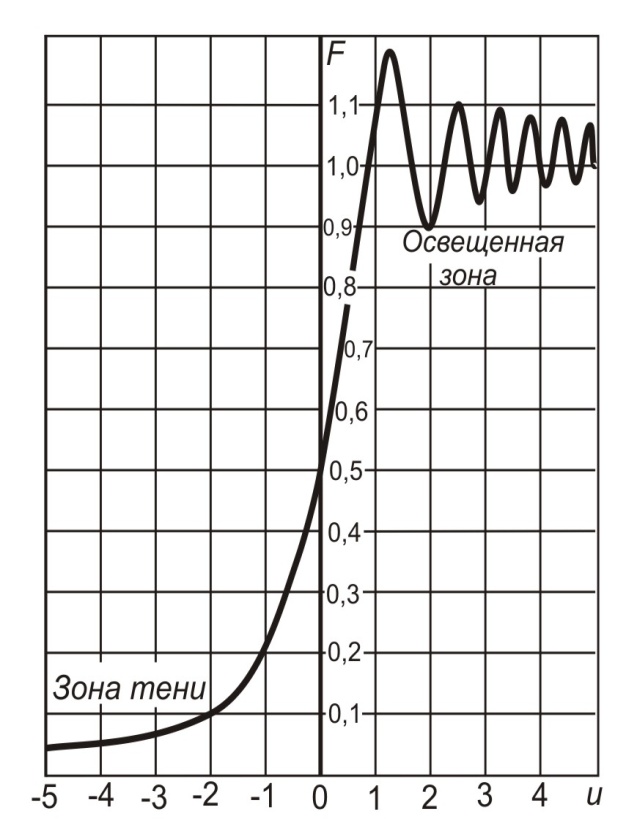 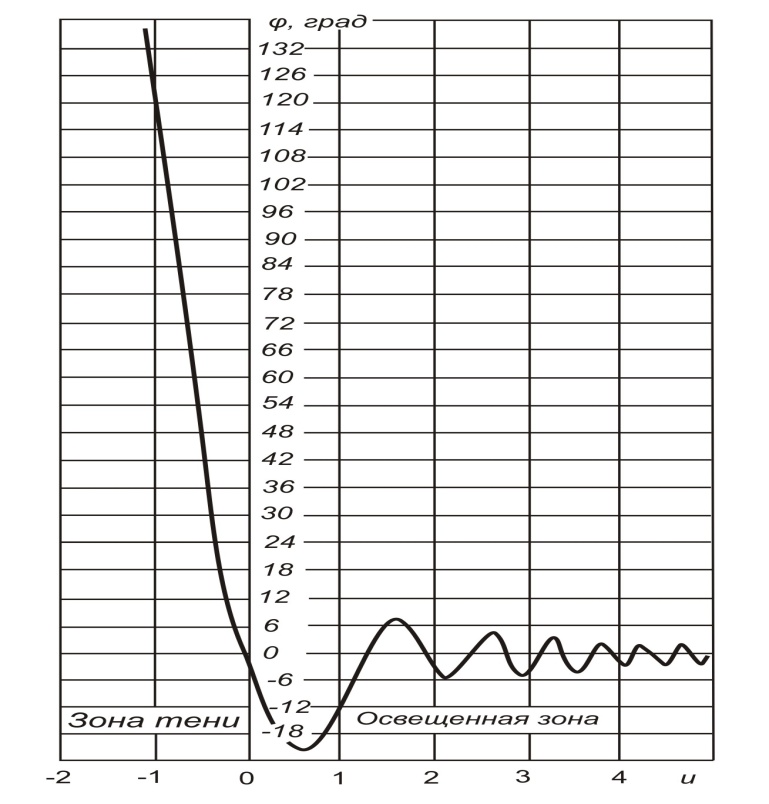
Cправа от нуля располагается положительные значения V0 (зоны освещённости), слева – отрицательные (зоны тени). Принципиально можно выделить четыре участка: 1) V0 > 1 (5> V0 >1) – это область осцилляции, где Н< Rф1; 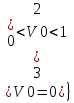 –это область спада, где Н=0,Н= Rф1, причем Н- положительная величина; –это область спада, где Н=0,Н= Rф1, причем Н- положительная величина;4) V0 < -1 – это область спада, где –Н= Rф1, -Н> Rф1 при чем Н - отрицательная величина Первая область: В освещенную зону входят две области, где V0 изменяется от 1 до 5 и от 0 до 1.Эта область соответствует истинным просветам +Н > 0.7Rф1. Здесь имеют место осцилляции относительного уровня (|V|=1), что в децибелах соответствует 0 дБ которые асимптотически затухают по мере увеличения V0. С увеличением V0 т.е. с увеличением Н ( 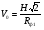 ) экранируются нижние участки зон Френеля с большими номерами (n > 2, чётные и нечётные). А так как поля от различных зон Френеля складываются векторно, то при экранировании нарушается амплитудные и фазовые соотношения между интерферирующими волнами, что приводит к осцилляциям рис.(). ) экранируются нижние участки зон Френеля с большими номерами (n > 2, чётные и нечётные). А так как поля от различных зон Френеля складываются векторно, то при экранировании нарушается амплитудные и фазовые соотношения между интерферирующими волнами, что приводит к осцилляциям рис.().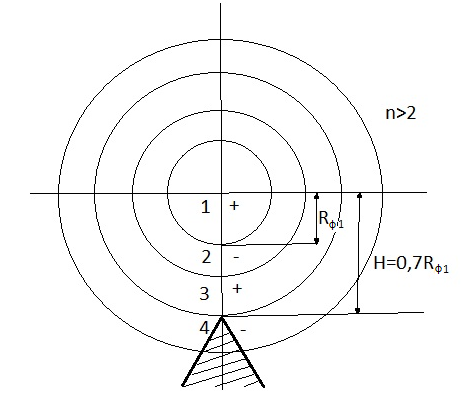 Рисунок - Первая область изменения множителя ослабления (5> V0 >1) Вторая область, третья область: При значениях 0<V0 < 1, просвет Н остается положительным но начинает уменьшатся по величине. | V| монотонно уменьшается и при V0=0.5 достигает значения | V|дБ = -1,94дБ . При V0 = 0, Н = 0 |V|дБ = -6 дБ ( 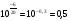 ) – точка наблюдения находится на линии геометрической тени, когда экран перекрывает половину площади всех зон и половину первой зоны Френеля включительно (рис.2,3 ). ) – точка наблюдения находится на линии геометрической тени, когда экран перекрывает половину площади всех зон и половину первой зоны Френеля включительно (рис.2,3 ).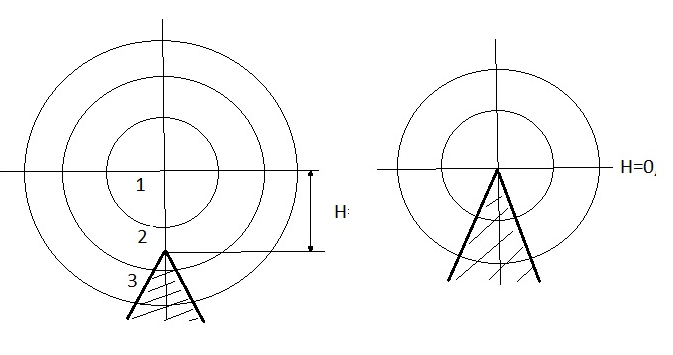 Рисунок - Вторая и третья область изменения множителя ослабления (0<V0 < 1,V0 =0) Четвертая область: При V0 < -1. Здесь поле создаётся участками зон Френеля не закрытыми препятствием. |V| монотонно убывает от -6 дБ до -26 дБ при V0 = -5. Существует особая точка, когда -Н = Rф1, то есть полностью перекрывает первую зону Френеля V0 = -1, |V|дБ = -14 дБ. При V0 = -2 , |V|дБ = -20 дБ рис.( ). 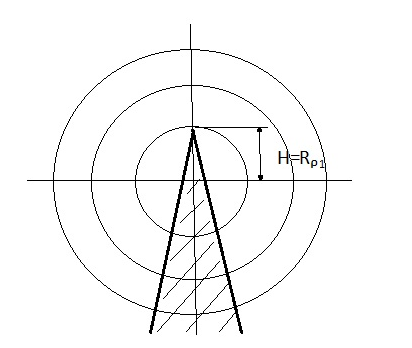 Рисунок - Четвертая область изменения множителя ослабления (V0 < -1 ) В пределах изменения V0 от -1 до -2, |V| можно считать по асимптотическим формулам : 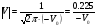 , ( ) , ( )или в дБ: 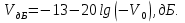 ( ) ( )Усиление препятствием (4-х лучевая теория дифракции) В диапазоне УКВ, кроме дифракции вокруг края непрозрачного экрана волн передатчика, необходимо учитывать дифракцию на этом же экране волн, отражаемых от поверхности Земли на участках: передающая антенна – экран и экран – приёмная антенна. Пусть на пути распространения радиоволн находится непрозрачный экран (клиновидное препятствие) (рис. ). Поле в точке приёма – это результат интерференции четырёх волн, каждая из которых дифрагирует у края непрозрачного экрана. Это волны АМВ, А’МВ, АМВ’, А’МВ’. Для определения результирующего множителя ослабления при данной дифракции используется метод зеркальных изображений. Суммирование полей возможно вследствие линейности системы. Все эти 4 луча дифрагируют на вершине клиновидного препятствия рис(). Для определения результирующего множителя ослабления введем обозначения (рис.): На участке передатчик-вершина препятствия М, АМ – прямой луч; АДМ - отраженный луч; разность хода лучей 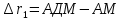 . На этом участке множитель ослабления . На этом участке множитель ослабления 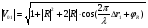 ( ) ( )На участке вершина-препятствие М- приемная антенна- МВ – прямой луч, МFB – отраженный луч; разность хода лучей 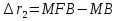 .На этом участке множитель ослабления .На этом участке множитель ослабления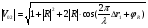 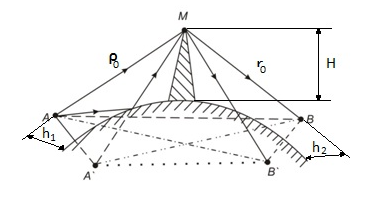 Рисунок - Дифракция у непрозрачного препятствия при учете отражений от поверхности Земли Результирующий множитель ослабления на такой трассе равен произведению трех множителей V=V0 V01V02 , ( ) где V01,V02 рассчитываются по формулам ( ) ,( ); V0 – множитель ослабления рассчитываемый по формуле Лансберга ( ), в результате дифракции на одиночном клиновидном препятствии в точке М, предварительно вычислив параметр дифракции 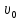 . . Для малых углов скольжения можно пользоваться формулой Введенского, если выполняеться условие 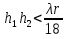 .В этом случае поле на краю экрана можно рассматривать как сумму прямой и отражённой волн от земной поверхности. Геометрия задачи приведена на рисунке .В этом случае поле на краю экрана можно рассматривать как сумму прямой и отражённой волн от земной поверхности. Геометрия задачи приведена на рисункеНа рисунке приняты обозначения: ρ0 – расстояние от А до М; r0 – расстояние от М до В; Н – высота препятствия; h1, h2 – высоты антенн. Множитель ослабления V01 по формуле Введенского на участке передающая антенна – препятствие будет равен. 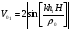 , ( ) , ( )где 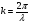 . . Множитель ослабления V02 на участке препятствие – приемная антенна, определится по формуле ( ). Поле в точке приёма – это суперпозиция двух волн, дифрагированных на краю экрана (прямой и отражённой). Это даёт второй множитель ослабления V02 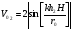 . ( ) . ( )Результирующий множитель ослабления 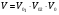 ; ; 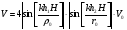 ( ) ( )или в дБ 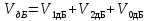 ( ) ( )4-х “лучевая” теория дифракции долго считалась идеализированной. Однако, при разработке линий УКВ было обнаружено явление «усиления» поля при огибании радиоволнами горных хребтов. Это явление неплохо объясняет 4-х лучевая трактовка. Сущность эффекта «усиления препятствием»
Это объясняется следующим:
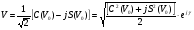 Для всех четырёх волн будут величинами одного порядка.
Дифракция на трассе, состоящей из нескольких препятствий Определение ослабления на трассах с несколькими препятствиями сводится к решению задачи о многократной дифракции. Задача о таком виде дифракции на ряде препятствий, в общем, очень сложна и строгое ее решение известно лишь для частного случая для двух препятствий. Если на трассе находится два или более хребтов, то каждый из них можно аппроксимировать клиновидным одиночным препятствием. (рис. ) Дифракция радиоволн на таком виде трассы рассматривается во многих теоретических работах. Дело в том, что в условиях горного рельефа практически никогда не известна точная форма препятствия. Если даже она известна, то ее практически не возможно сколько-нибудь уверенно аппроксимировать какими-либо геометрическими поверхностями. Неровности горного рельефа настолько сложны, что точное их отображение является непосильной задачей. Поэтому методы расчета не стоит усложнять излишней строгостью, так как они не дают на практике заметных улучшений по сравнению с «грубыми» методами, которые будут использоваться в этом разделе. В случае дифракции на нескольких препятствиях общий множитель ослабления будет произведением множителей ослабления отдельных участков, что является следствием малости существенной области при дифракции на препятствиях с малым радиусом кривизны. Если на трассе имеется n препятствий, то общий множитель ослабления 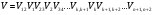 , ( ) , ( )где 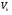 - это ослабление на k-ом препятствием; - это ослабление на k-ом препятствием; 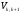 - ослабление на трассе между k-ым и k+1-м препятствиями в предположения, что корреспондирующие пункты находятся на вершинах этих препятствий. Множители - ослабление на трассе между k-ым и k+1-м препятствиями в предположения, что корреспондирующие пункты находятся на вершинах этих препятствий. Множители 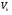 определяются с учетом того, что предыдущее препятствие изменяет направление прихода волны. Волна приходит не из точки расположения источника, а с направления, совпадающего с направлением от вершины предыдущего препятствия на вершину рассматриваемого препятствия. В результате дифракции на предыдущем препятствии источник как бы поднимается до линии, соединяющей рассматриваемые препятствия с предыдущим при неизменном расстоянии от рассматриваемого препятствия до источника. Точно такое же положение будет и в случае препятствий произвольной формы с малым радиусом кривизны. Это следует из того факта, что существенная область при интегрировании по источникам Гюйгенса, расположенными на плоскости, проходящей через рассматриваемое препятствие, мала из-за малого радиуса кривизны препятствия. Таким образом множитель определяются с учетом того, что предыдущее препятствие изменяет направление прихода волны. Волна приходит не из точки расположения источника, а с направления, совпадающего с направлением от вершины предыдущего препятствия на вершину рассматриваемого препятствия. В результате дифракции на предыдущем препятствии источник как бы поднимается до линии, соединяющей рассматриваемые препятствия с предыдущим при неизменном расстоянии от рассматриваемого препятствия до источника. Точно такое же положение будет и в случае препятствий произвольной формы с малым радиусом кривизны. Это следует из того факта, что существенная область при интегрировании по источникам Гюйгенса, расположенными на плоскости, проходящей через рассматриваемое препятствие, мала из-за малого радиуса кривизны препятствия. Таким образом множитель 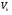 определяется следующим образом. Через вершины k-1 и k –ого препятствий проводится линия; определяется следующим образом. Через вершины k-1 и k –ого препятствий проводится линия; 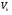 - это ослабление, вызванное препятствием, когда источник находится на этой линии в точки - это ослабление, вызванное препятствием, когда источник находится на этой линии в точки 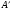 , а приемник на вершине k –ого препятствия (рис. 37). , а приемник на вершине k –ого препятствия (рис. 37). Рисунок - Дифракция на многих препятствиях. Кажущееся положение передающего пункта А’. Наиболее удобно при расчете разбить всю трассу пополам и рассчитать ослабление для каждой половины трассы. Ослабление средним препятствием считать так, будто источник и приемник подняты до линии, соединяющих вершину соседнего препятствия с вершинами соседних препятствий (рис.38). 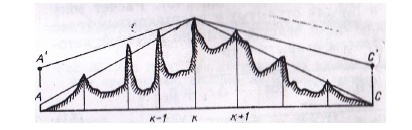 Рисунок - Определение ослабления на k-ом препятствии с помощью введения кажущихся положений корреспондирующих точек А’,C’ Такой метод дает наиболее точные результаты, удовлетворяющие теореме взаимности. Физическая основа этих исследований состоит в следующем. 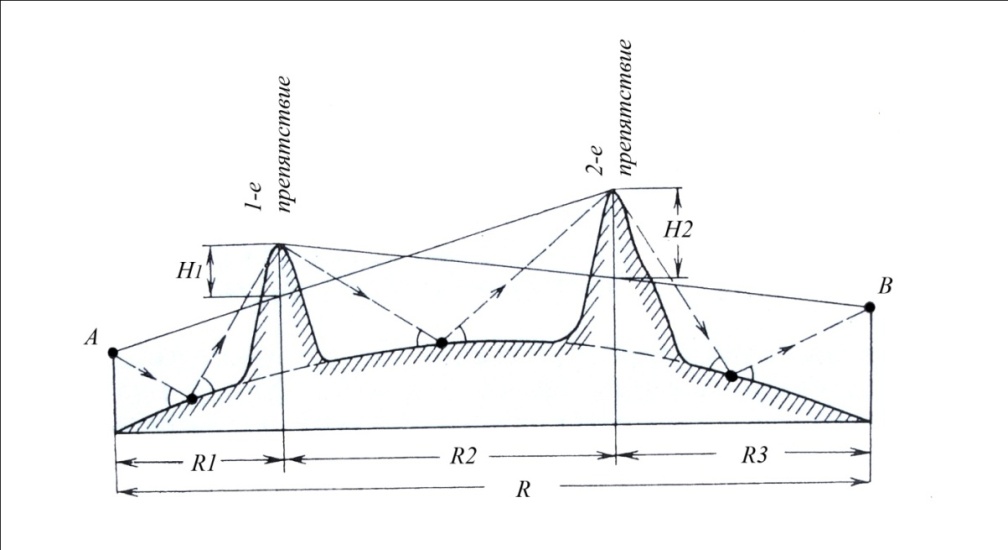 Рисунок - Дифракция на двух препятствиях Известно, что при дифракции на одиночном клиновидном препятствии, поле в точке приёма В определятся излучением вторичных источников, расположенных на незатенённой части плоскости проходящей через экран (препятствие №1). Интенсивность каждого источника зависит от расстояния до точки передачи А. При дифракции на двух клиновидных препятствиях (рис.) поле в точке приёма В определяется путём интегрирования по незатенённой части плоскости, проходящей через второй экран. Интенсивность источников будет зависеть не только от расстояния до точки излучения А, но и от влияния экрана №1.(рис. ) Это влияние учитывается на основании решения задачи о дифракции на одиночном клиновидном препятствии. Аналогичные рассуждения можно провести и на числе клиновидных препятствий, больше двух.(рис. ) 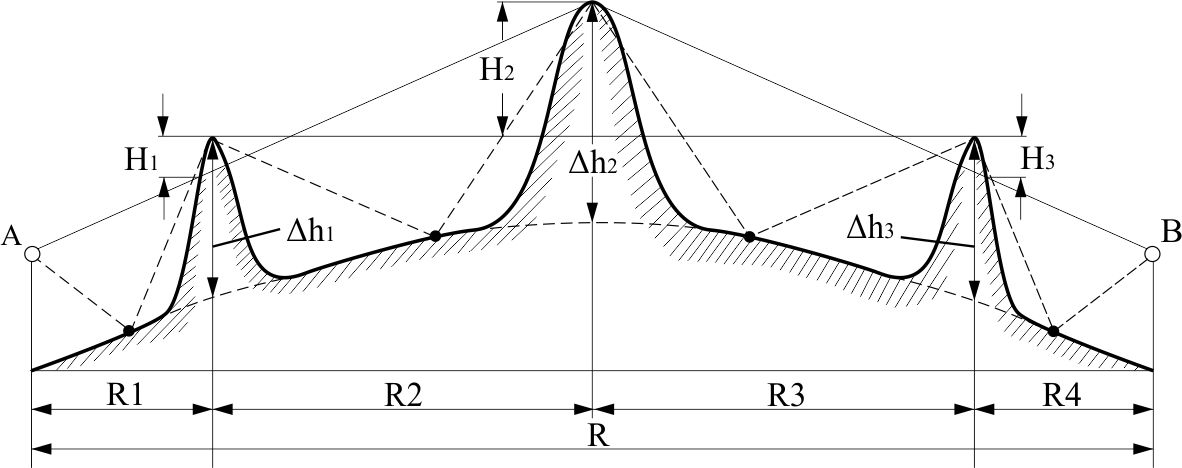 Рисунок - Дифракция на трех препятствиях Несмотря на то, что физическая картина дифракции радиоволн на нескольких препятствиях достаточно проста, строгое определение множителя ослабления сопряжено с многими трудностями. Простые расчётные формулы могут быть получены лишь для некоторых частных случаев.
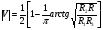 , где , где 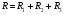
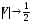 (-6 дБ) (-6 дБ)в этом случае оба препятствия дают такое же ослабление, как и одно препятствие.
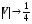 (-12 дБ), (-12 дБ),т.е. при R2 достаточно большом по сравнению с R1 и R3, общее ослабление равно произведению (или сумме в дБ) ослаблений, вносимым каждым препятствием в предположении отсутствия другого.
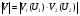 или в дБ 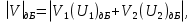 где 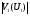 и и 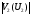 - модули множителя ослабления на одиночном клиновидном препятствии. В них - модули множителя ослабления на одиночном клиновидном препятствии. В них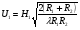 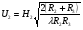 Физическое истолкование процесса многократной дифракции на клиновидных препятствиях: Вершина 1-го препятствия считается как некоторый эквиалентный источник, излучение, которого ослаблено множителем 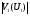 . Вершину второго препятствия – новый эквивалентный источник, излучение которого ослаблено в . Вершину второго препятствия – новый эквивалентный источник, излучение которого ослаблено в 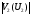 и т.д. Этот подход может применяться и на число препятствий больше трёх, но только при условии, что значения всех аргументов U1, U2, U3 и т.д. меньше, чем (0,5 ÷ 1). и т.д. Этот подход может применяться и на число препятствий больше трёх, но только при условии, что значения всех аргументов U1, U2, U3 и т.д. меньше, чем (0,5 ÷ 1).В формуле для множителя ослабления 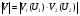 не учитываются отражения волны, которые могут возникать на участке АВ между препятствиями (пунктирные линии), если местность между ними достаточно ровная. С учётом отражения 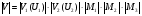 , где , где|M1|, |M2|, |M3| - модули интерференционных множителей на участках: А – 1 препятствие; 1 – препятствие – 2 препятствия; 2 препятствия – т. В. Они могут быть определены как это делалось в разделе «Поле в зоне прямой видимости»; отличие в том, что в формуле разности хода между прямой и отражённой волнами и углом скольжения следует подставлять длины соответствующих участков и соответствующие высоты вершин препятствий или корреспондирующих точек. При наличии на трассе большого количества препятствий дать простые расчётные формулы трудно. Для этих случаев расчет множителя ослабления приводится в [ ] Троицкий В.Н. Распространение УКВ в горах. «Связь» 1968. «Инженерно-технический справочник по электросвязи. Радиорелейные линии». Связь. М. 1971 г. Распространение радиоволн в условиях большого города Любую радиотрассу можно представить в виде набора нескольких основных путей, по которым сигнал от базовой станции доходит до приёмной антенны и наоборот. На каждом из этих путей находятся различные объекты, влияющие на распространение радиоволн. В городских условиях это:
Т.е. большой город можно рассматривать как сильно пересечённую местность: |

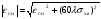 ;
; 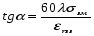 ;
; 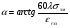 ;
; 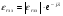 .
.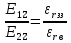
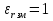 Н1У = Н2У
Н1У = Н2У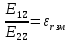
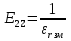
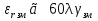 , то
, то