ЗВ и мобильная связь 2010. Запорізький національний технічний університет
 Скачать 37.31 Mb. Скачать 37.31 Mb.
|
|
Интерференционный минимум наблюдается в направлении для которых: 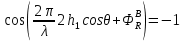 А это возможно если аргументы принимают значения 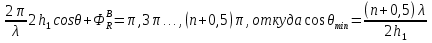 Тогда множитель ослабления в минимуме (для идеально проводящей Земли) для этого случая запишется: 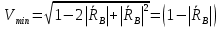 () ()Амплитуды результирующего поля с учетом интерференционных максимумов и минимумов будут равны. 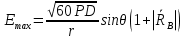 () ()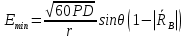 () ()С учетом формул () и () можно сказать, что ДН диполя будет иметь лепестковый характер, вследствие интерференции. В полярной системе координат ДН будет иметь вид (рис. ).Таким образом, при углах θmax амплитуда поля увеличивается в (1 + Rв) раз, а при θmin уменьшается в (1 – Rв) раз, за счет влияния поверхности земли. 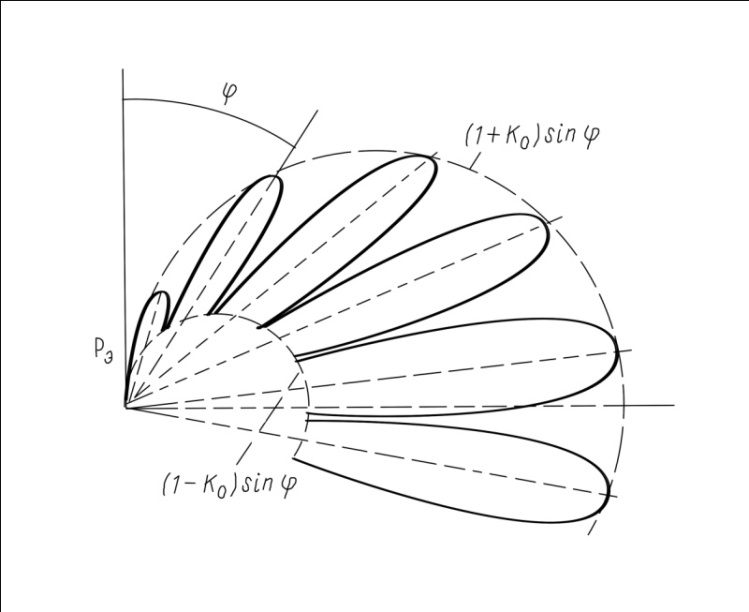 Рисунок - Диаграмма направленности вертикального диполя вследствие явления интерференции Рассмотрим влияние на ДН параметров поверхности Земли над которой происходят излучение. В случае идеально проводящей поверхности при любых углах падения волны 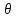 , коэффициент равняется , коэффициент равняется 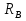 = 1, = 1,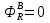 . Преобразуем выражение (). . Преобразуем выражение ().Тогда 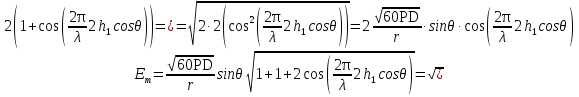 Первый максимум будет при 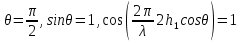 Тогда 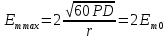 , т.е. в горизонтальном направлении при , т.е. в горизонтальном направлении при 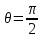 будет первый максимум рис ( ). В направлениях максимума Еm будет достигать двойного значения. В направлениях минимума – излучение будет отсутствовать.(рис. ) будет первый максимум рис ( ). В направлениях максимума Еm будет достигать двойного значения. В направлениях минимума – излучение будет отсутствовать.(рис. )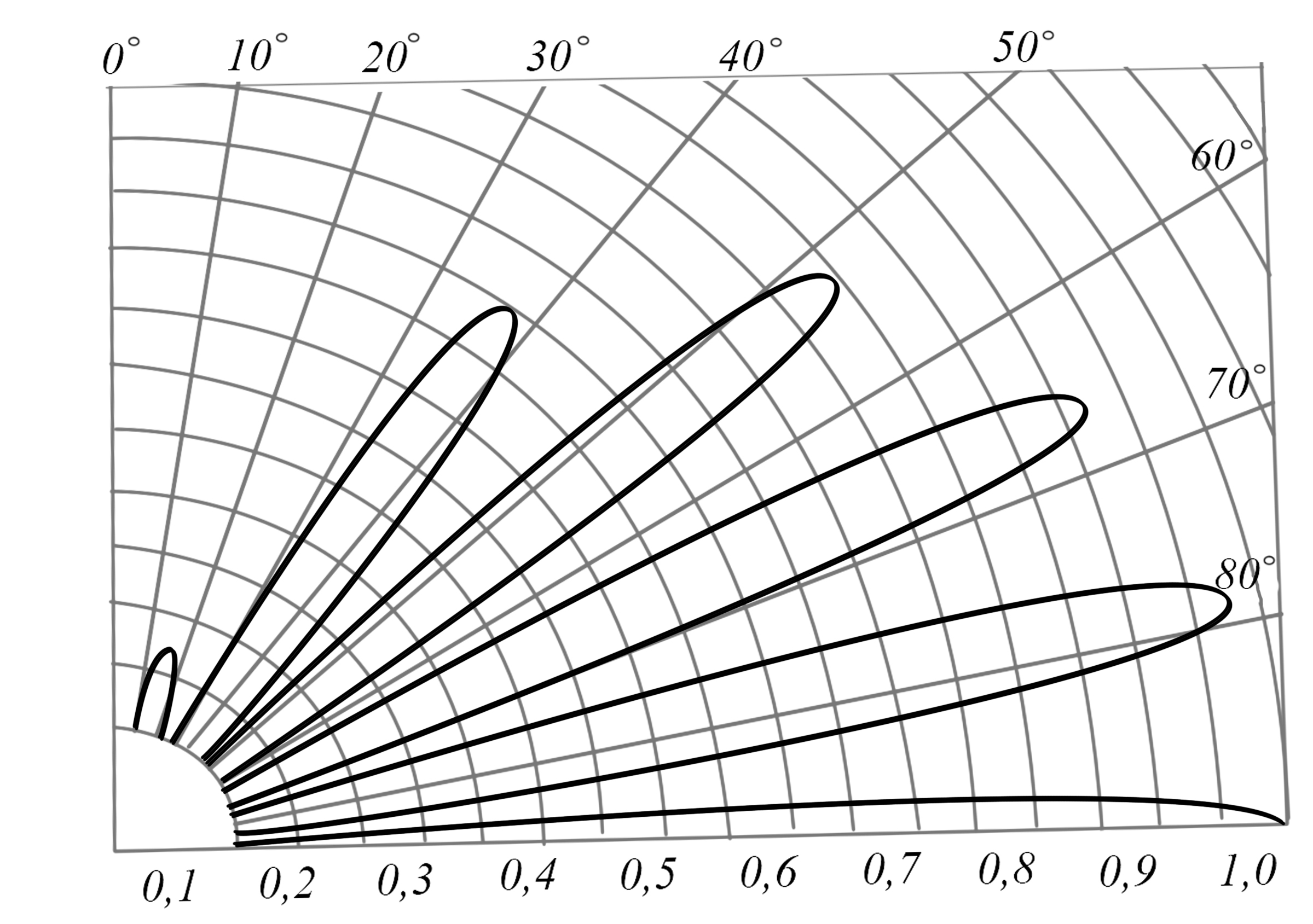 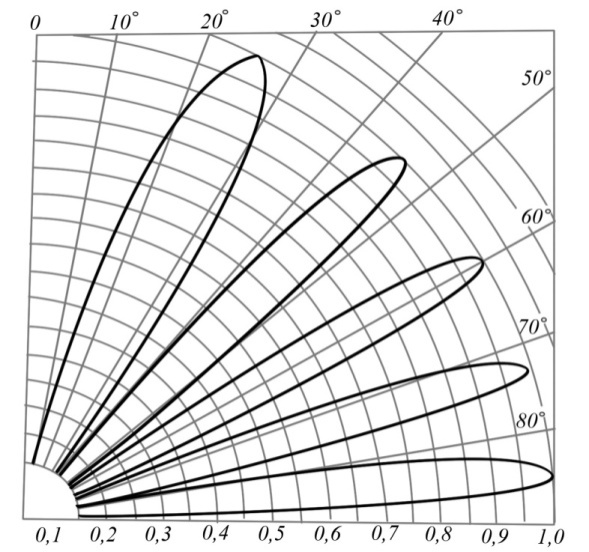 Рисунок 1 Рисунок 2 Рисунок 1 – Диаграмма направленности вертикального диполя, расположенного на высоте 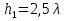 над идеально проводящей поверхностью над идеально проводящей поверхностью Рисунок 2 - Диаграмма направленности горизонтального диполя, расположенного на высоте 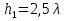 над идеально проводящей поверхностью над идеально проводящей поверхностью Горизонтальный диполь. Рассмотрим электрическое поле горизонтального диполя в его экваториальной плоскости. В этой плоскости диполь не обладает направленными свойствами 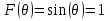 и создает в дальней зоне горизонтально-направленное результирующее поле. и создает в дальней зоне горизонтально-направленное результирующее поле.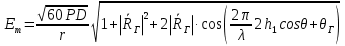 () ()Полученное выражение отличается от уравнения () только заменой 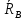 на на 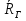 и отсутствие множителя и отсутствие множителя 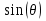 . Поэтому направление максимумов и минимумов излучения определяется . Поэтому направление максимумов и минимумов излучения определяется 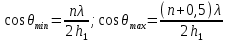 . .Структура поля лепестковая как и для вертикального вибратора, но направление максимумов и минимумов излучения меняются местами по отношению к полю вертикального вибратора.(рис. ) Так как 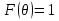 , то амплитуда лепестков не меняется в зависимости от угла θ. При , то амплитуда лепестков не меняется в зависимости от угла θ. При 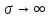 ; ; 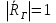 ; ; 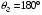 Тогда возможно излучение вверх, а вдоль земли излучения нет. Интерференционные формулы Введенского. В наиболее важном для распространения УКВ вдоль поверхности Земли случае пологих лучей (θ→90o) формулы для определения поля вертикального и горизонтального вибратора можно подвергнуть дальнейшему упрощению. Приближенно можно считать 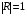 , , 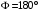 . .То есть представляет интерес изменение множителя ослабления с расстоянием r при заданных высотах антенн. Чтобы установить эту зависимость, необходимо найти другое выражение разности хода прямого и отраженного лучей. При условии r>>h1, r>>h2. (рис. ) 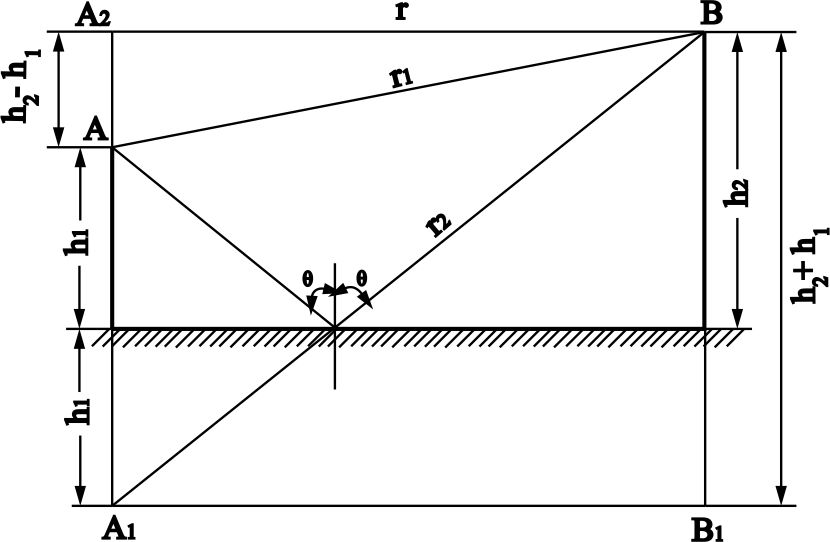 Рисунок - К определению результирующего поля в месте приема ( квадратичная формула Введенского) Определим путь прямой и отраженной волн: Из Δ AA2B определим r1: 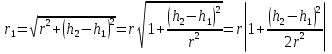 Из Δ A1BB1 определим r2 : 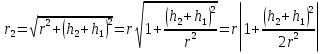 Тогда разность хода лучей прямой и отраженной волн определится, как 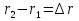 Выполнив несложные преобразования , находим 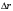 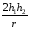 = Тогда коэффициент ослабления V будет равен 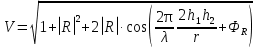 Дальностная характеристики (зависимость V от расстояния r) При изменении r множитель ослабления V проходит ряд максимумов, когда в точке приема прямая и отраженная волна приходят в одинаковых фазах, а именно 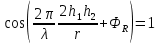 или аргумент или аргумент 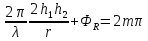 , где m= 1, 2, 3… , где m= 1, 2, 3…и ряд минимумов, то есть прямая и отраженная волна приходят в противофазе, то есть 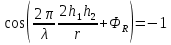 или или 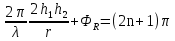 , где n= 1, 2, 3… , где n= 1, 2, 3…В максимумах 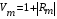 – огибающая в максимумах. – огибающая в максимумах.В минимумах 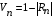 – огибающая в минимумах. – огибающая в минимумах.Множитель ослабления может быть больше единицы, поэтому его правильней назвать интерференционным. Зависимость имеет интерференционный лепестковый характер. Интерференционные минимумы. С уменьшением r ширина лепестков уменьшается из-за гиперболической зависимости разности хода 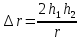 от расстояния, а значение от расстояния, а значение 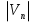 в минимумах увеличивается за счет увеличения угла скольжения в минимумах увеличивается за счет увеличения угла скольжения 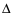 , а следовательно, из-за уменьшения , а следовательно, из-за уменьшения 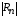 . .В интерференционных min при 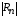 близких и единице необходимо определять близких и единице необходимо определять 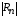 с большей точностью, так как с большей точностью, так как 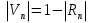 (рис. ). (рис. ). 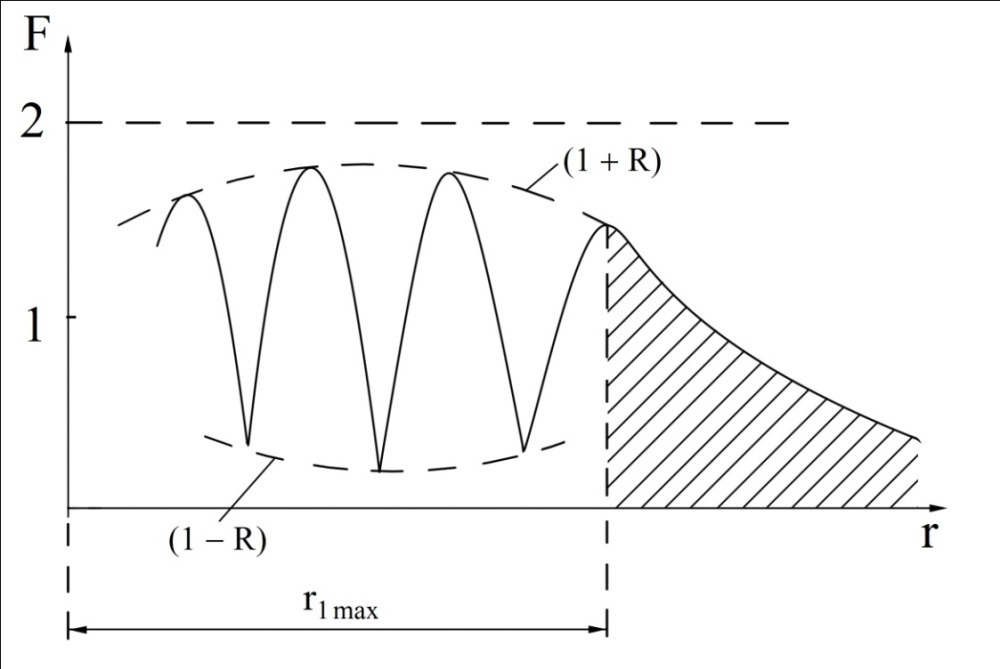 Рисунок - Зависимость множителя ослабления от расстояния в общем случае Интерференционные максимумы. При малых углах скольжения, которые обычны для линий связи, значение 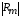 близки и единице, поэтому можно считать без заметной ошибки, что близки и единице, поэтому можно считать без заметной ошибки, что 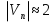 в интерференционные максимумах. в интерференционные максимумах.Высотная зависимость Зависимость V(h2) приведена на рис. . 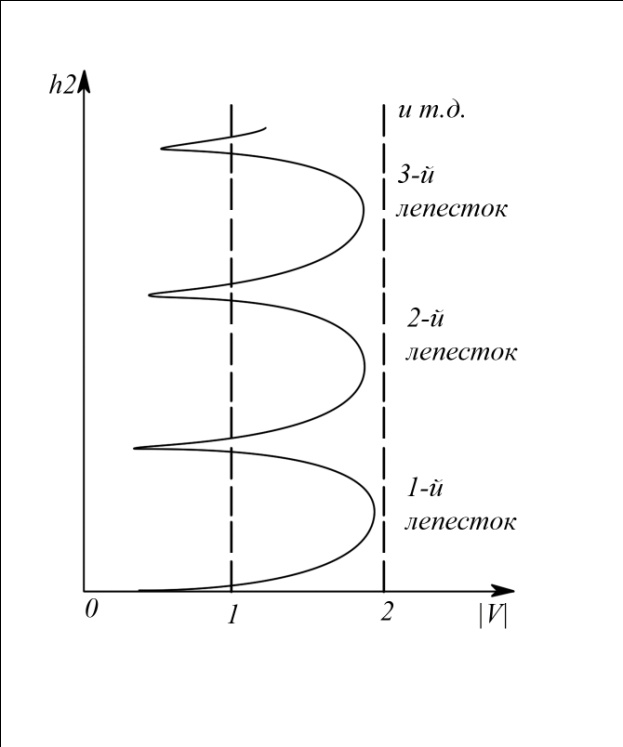 Рисунок - Высотная зависимость множителя ослабления Из графика видно, что ширина лепестков не зависит от h2, из-за линейной зависимости Δr от h2. 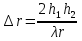 Глубина минимумов с увеличением 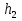 уменьшается за счет увеличения углов скольжения, а, следовательно, уменьшения уменьшается за счет увеличения углов скольжения, а, следовательно, уменьшения 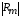 . .Формулы Введенского. Критерий применимости. Во многих случаях формулу для V можно упростить. При малых углах скольжения для большинства видов поверхности Земли (на практике) коэффициент отражения 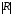 близок к единице, а фаза коэффициента близок к единице, а фаза коэффициента 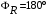 , это особенно справедливо для горизонтально поляризованного излучения. , это особенно справедливо для горизонтально поляризованного излучения.Тогда 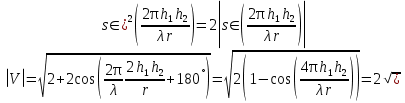 Множитель ослабления имеет синусоидальный закон изменения. 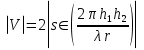 ( ) ( )Если r выразить в км, а угол в градусах, получим инженерную формулу: 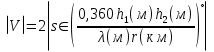 ( ) ( )Зависимость множителя ослабления V( r ) при отсутствии потерь при отражении от земли имеет вид (рис.): 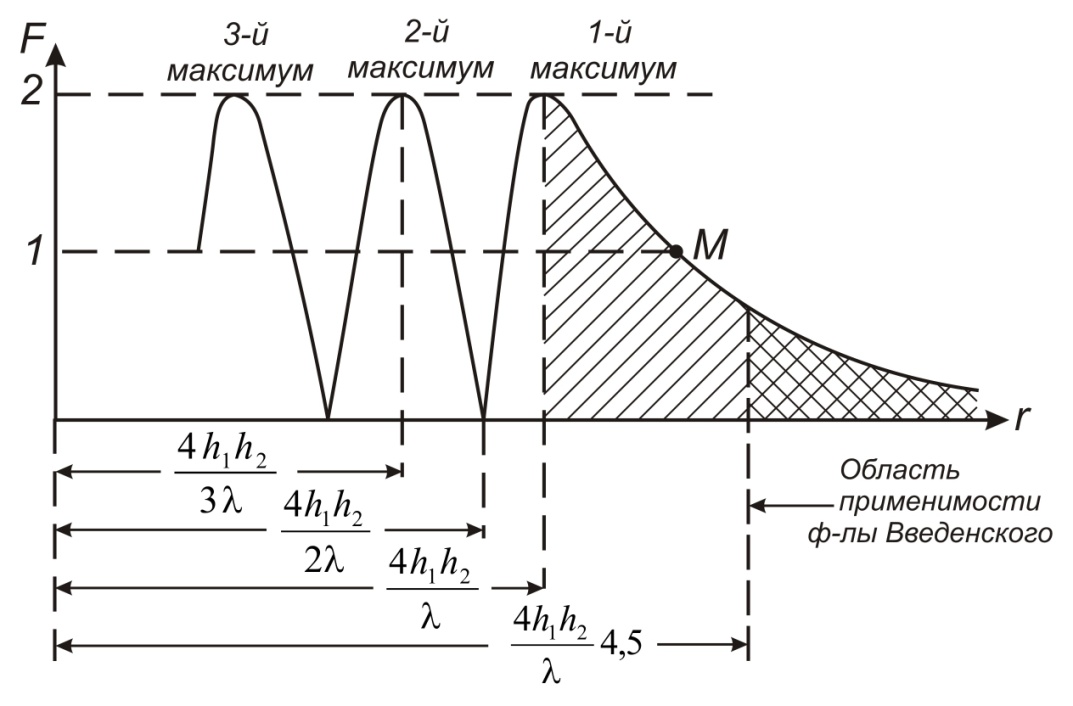 Рисунок - Зависимость множителя ослабления от расстояния при 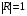 Определим расстояния, которым соответствуют максимумы и минимумы. Максимумы находятся из условия: 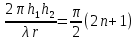 , ,где n=0,1,2,3… Тогда 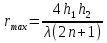 Следовательно, 1-ый max, считая со стороны больших расстояний, удален от передатчика на расстояние 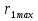 при n=0 и формула при n=0 и формула 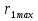 будет иметь вид: будет иметь вид: 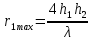 ( ) ( )Получим положение 2-го максимума 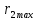 при n=1 при n=1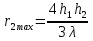 ( ) ( )Минимумы находятся из условия 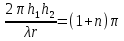 , ( ) , ( )где т=0,1,2,3… Отсюда можно определить положение минимумов: 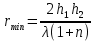 ( ) ( )Таким образом, первый минимум расположен на расстоянии 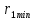 при n=0 при n=0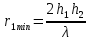 ( ) ( )В рассматриваемом случае, в отличие от общего случая, максимальные значения 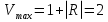 А минимальные 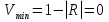 С некоторого расстояния 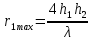 – соответствующему 1-му интерференционному лепестку |V| монотонно убывает, стремясь в пределе к нулю. Это объясняется тем, что с увеличением r, Δr→0 траектории прямой и отраженной волны сливаются. – соответствующему 1-му интерференционному лепестку |V| монотонно убывает, стремясь в пределе к нулю. Это объясняется тем, что с увеличением r, Δr→0 траектории прямой и отраженной волны сливаются.Дальнейшее упрощение формулы Введенского Во многих для практики случаев формуле () можно придать более простой и удобный для расчетов вид. Если аргумент синуса в формуле () для V меньше 20o, то есть π/9, то есть при условии 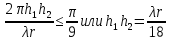 то синус можно заменить его аргументом и V будет равняться: 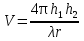 ( ) ( )Напряженность поля с учетом () в точке приема будет равна 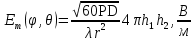 Или действующее значение Едейств , выразив мощность Р в кВт, 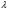 в метрах, h1 и h2 в метрах, и r в км получим квадратичную формулу Введенского в метрах, h1 и h2 в метрах, и r в км получим квадратичную формулу Введенского 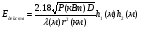 , (мВ/м) , (мВ/м) Эта формула была получена академиком Введенским и носит его имя. Ограничения для использования формулы Введенского. Для использования формулы Введенского имеются существенные ограничения: 1. Должны выполняться условия 0,95 < |R| и 175o < θ < 180o, что легче выполняются для горизонтальной поляризации волн и труднее для вертикальной поляризации. 2. Формула применима только для антенн, поднятых над землей, то есть высоты h1 и h2 > λ в несколько раз (по крайней мере). В этом случае можно пользоваться приближенной трактовкой о существовании в месте приема прямого и отраженного луча. Если это условие не выполняется, то необходимо учитывать влияние плоской полупроводящей поверхности Земли и расчет поля в точке приема вести строго. 3. Формула применима при выполнении условия 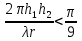 Только в этом случае sin можно заменить его аргументом 4.Для формулы Введенского характерно квадратичное убывание напряженности поля 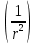 с расстоянием, убывание более быстрое, чем в свободном пространстве с расстоянием, убывание более быстрое, чем в свободном пространстве 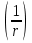 . . Частный случай (низкорасположенные антенны) Для антенн (безразлично передающая или приемная), находящихся на Земле, например, h2 = 0, напряженность поля нельзя считать по формуле Введенского, так как Еm обращается в нуль, что не соответствует реальности. В этих условиях излучаемые волны поглощаются на всем пути, а не только в точке отражения. В инженерной практике приводится упрощенный метод расчета |V| для небольших высот антенн 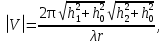 где h0 – минимальная эффективная высота антенн. Минимальная эффективная высота для вертикальной поляризации можно определить из формулы 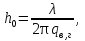
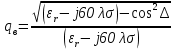
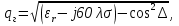 где 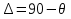 - угол встречи. - угол встречи.Если h1 >> h0 и h2 >> h0, то 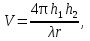 Если, наоборот, h1 << h0 и h2 << h0, то 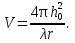 Ясно, что при низко расположенных антеннах множитель ослабления V не зависит от высот антенн. Распространение радиоволн над неровной или неоднородной трассой, когда антенны высоко подняты над землёй. Критерий Рэлея На земной поверхности имеются более или менее выраженные неровности, наличие которых влияет на распространение радиоволн. В общем случае учесть это влияние не представляется возможным. Поэтому в каждом конкретном случае строится профиль трассы и затем ведётся расчёт тем или иным способом. Виды неровностей: мелкие неровности (шероховатая поверхность), пологие холмы, город, одиночные препятствия (гора, высокий дом). Отражение радиоволн от неровной (шероховатой) земной поверхности. Критерий Рэлея Из курса технической электродинамики известно, что при падении волны на совершенно ровную поверхность, направление отражённой волны определяется по закону геометрической оптики (φ = φ’ первый закон Снеллиуса). Такое отражение называется зеркальным. Только при нормальном падении отражённая волна возвращается излучателю. Если поверхность земли неровная, то радиоволны отражаются в разных направлениях, в том числе в обратном (рис ). 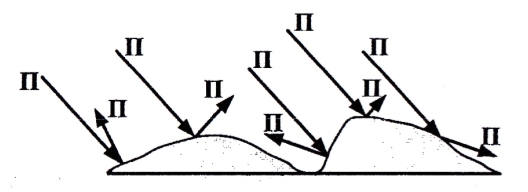 Рисунок - Возникновения рассеянных отражений от шероховатой поверхности В оптике для оценки степени шероховатости отражающей поверхности широко пользуются критерием Рэлея. Это понятие применимо и при излучении вопросов распространения радиоволн. Критерий Рэлея Задача формируются следующим образом: пусть имеется шероховатая поверхность, на которую под углом Θ падают радиоволны (рис ). Допустим, что все неровности имеют одинаковую высоту h, что даёт возможность говорить о средней высоте неровностей. 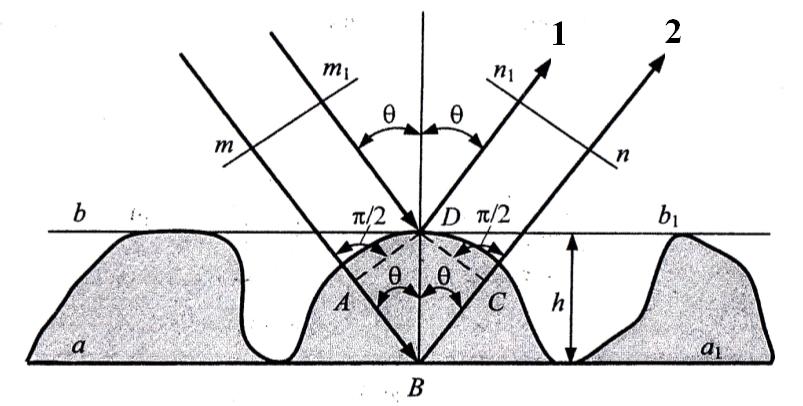 -верхний уровень -нижний уровень Рисунок - К установлению критерия Рэлея В создании отражённой волны принимают участие и нижний и верхний уровни. Пл. m-m1 - плоскость равных фаз падающих волн, а плоскость n-n1 - это плоскость равных фаз отраженных волн. Определим фазовые соотношения на плоскости n-n1. Волны отражающиеся от нижнего уровня проходят дополнительный путь ABC=2hcos Θ. Это вызывает сдвиг фаз между лучами 1 и 2 равный 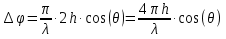 ( ) ( )Считают, что если фазовые искажения на плоскости n-n1 не превышают 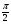 , то волну можно считать плоской и влиянием неровностей на отражение волны пренебречь. , то волну можно считать плоской и влиянием неровностей на отражение волны пренебречь. Из этого условия можно получить допустимую высоту неровностей, при которых отражение можно считать зеркальным: 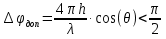 Откуда 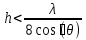 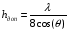 . ( ) . ( )Это соотношение называется критерием Рэлея. Он показывает, что при данной высоте неровностей зеркально отражаться будут лучи, полого падающие. Чем короче λ, тем сильнее сказывается неровности. В диапазоне УКВ даже небольшие неровности вызывают рассеяние отражённых волн. Неровной поверхностью является также поверхность взволнованного моря, причём степень неровности зависит от силы волнения. В ДВ и СВ - диапазонах неровности - холмы высотой десятки метров и крупные строения . Область поверхности, существенная при отражении. Первая зона Френеля при отражении По законам геометрической оптики отражение радиоволн отражение радиоволн происходит в некоторой точке. В действительности, согласно волновой теории, отражённая волна формируется участком земной поверхности, окружающим точку отражения. Если передающая и приёмная антенны разнесены на расстояние r, то как известно, в точку приёма приходят прямая и отражённая волны. Для каждой из этих волн имеется область существенная при распространении. Для прямой волны – это эллипсоид вращения с полюсами в точках А и В. 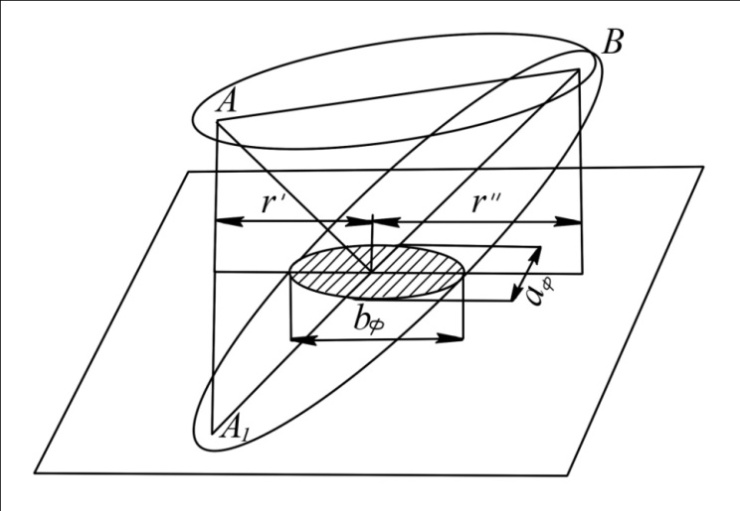 Рисунок - Построение существенной области при отражении Для отражённой волны – строят такой же эллипсоид с одним фокусом, находящимся в точке в т. А’ (фиктивный источник А’, согласно МЗИ). Область пересечения этого эллипсоида с земной поверхностью, представляет собой область, существенную при отражении радиоволн и имеет конфигурацию эллипса, большая ось которого вытянута в направлении распространения волны. Это первая зона Френеля при отражении. Расположение области на трассе оценивается расположением центра эллипса – точкой С.
Расположение области существенной на трассе оценивается расположением центра эллипса точкой С. При определении размеров эллипса возможны два варианта Первый вариант - 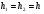 . .Второй вариант - 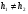 . .Рассмотрим первый вариант. В этом случае точка С располагается на середине трассы, тогда размеры определяются таким образом, если известен угол падения θ (рис ). 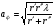 ( ) ( )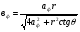 ( ) ( )Если известен угол скольжения ∆ .Тогда размеры эллипса вычисляются по формулам 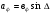 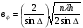 , ( ) , ( )где 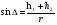 . .В практических расчетах n=1, в инженерных n=8. Из формул ( ) видно, что на реальных радиолиниях, когда 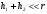 и и 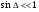 , размер , размер 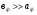 , то есть существенная область при отражении вытянута вдоль трассы и тем больше вытянута, чем ниже установлены антенны и длиннее трасса. В пределе когда , то есть существенная область при отражении вытянута вдоль трассы и тем больше вытянута, чем ниже установлены антенны и длиннее трасса. В пределе когда 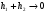 , то вся трасса становится существенной областью при отражении. Следовательно в этом случае отражательная трактовка влияния земли неприемлема. , то вся трасса становится существенной областью при отражении. Следовательно в этом случае отражательная трактовка влияния земли неприемлема.Второй вариант, когда 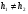 . . Уравнение этого эллипсоида можно получить, решив совместно уравнение эллипсоида вращения и уравнение отражающей плоскости. Опуская довольно громоздкие промежуточные выкладки, запишем формулы для определения большой оси эллипса 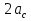 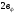 , малой оси , малой оси 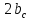 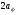 , смещения центра эллипса , смещения центра эллипса 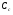 относительно геометрической точки отражения, предполагая, что существенная область охватывает первые 8 зон Френеля. относительно геометрической точки отражения, предполагая, что существенная область охватывает первые 8 зон Френеля.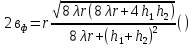 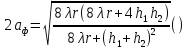 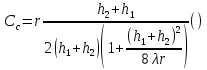 В реальных условиях 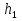 и и 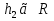 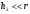 , поэтому эллиптическая существенная зона отражающей поверхности очень вытянута вдоль трассы , поэтому эллиптическая существенная зона отражающей поверхности очень вытянута вдоль трассы 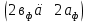 . . Из формулы () для Сс видно, что центр эллипса совпадает с точкой отражения, только в случае, когда 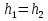 , т.е. равенству высот передающих и принимающих антенн. , т.е. равенству высот передающих и принимающих антенн.При 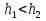 он сдвинут к точке приема он сдвинут к точке приема 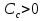 . .При 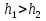 он сдвинут к точке передачи он сдвинут к точке передачи 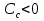 . .Напряжённость электрического поля над неровной поверхностью Напряжённость электрического поля над неровной поверхностью рассчитывается по тем же формулам, которые были получены для вертикального и горизонтального вибраторов, но только с учётом эффективного коэффициента отражения. Излучение в направлении интерференционных максимумов и минимумов описываются теми же выражениями, как и для вертикального и горизонтального диполя, отсюда можно получить выражение для эффективного коэффициента отражения от реальной земной поверхности: 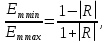 отсюда 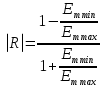 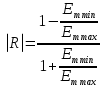 ( ) ( ) Этим методом определения Rэфф пользуются на практике: изменяя высоты антенн h1 и h2 ведут измерения Rэфф в широком диапазоне углов падения волн. Практические рекомендации: при распространении радиоволн над неоднородной поверхностью прежде чем рассчитывать напряжённость электрического поля, необходимо определить положение и размеры отражающей поверхности. Например, если отражающая поверхность попадает на ограниченную водную поверхность – озеро, а передающая и приёмная антенны находятся на суше на большом удалении от берега, то коэффициент отражения берётся от водной поверхности и характер поля будет такой, как если бы вся трасса проходила над водой. Трассы, проходящие над холмистой местностью Наиболее распространённым случаем является случай, когда:
Отличие распространения радиоволн над ровной поверхностью от холмистой местности состоит в том, что в первом случае формируется один отражённый луч, а в холмистой местности могут возникнуть несколько лучей.(рис.) 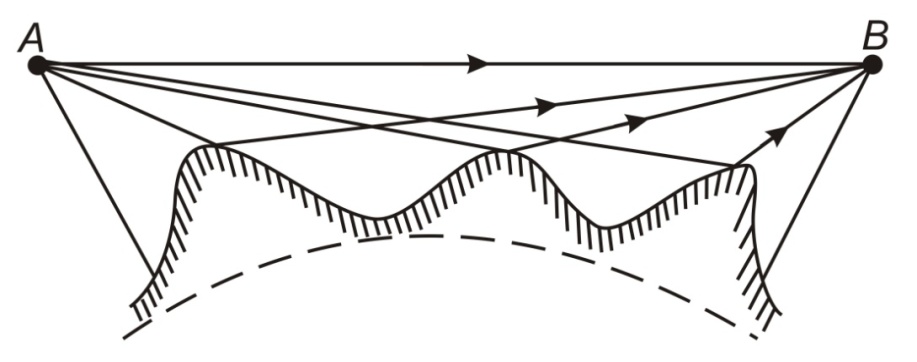 Рисунок – Распространение радиоволн в пределах прямой видимости над холмистой местностью Причём формирование отражённого луча происходит не в геометрической точке, а в пределах площади, ограниченной первой зоной Френеля при отражении и причём в подавляющих случаях размеры вершин холмов значительно меньше площади первой зоны Френеля. Типичные условия, в которых проходит трасса радиорелейной линии в холмистой местности показано на рисунке ( ). 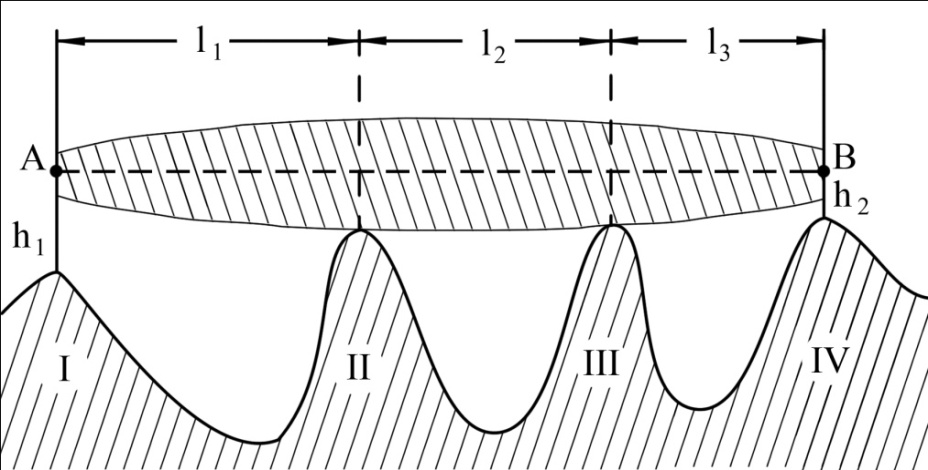 Рисунок – Определение необходимых высот антенн при распространении УКВ в холмистой местности Здесь l1, l2, l3 – расстояния между вершинами холмов. В заштрихованной области распространяется энергия волны, ограниченная І зоной Френеля. Здесь «опасными» зонами являются вершины ІІ и ІІІ холмов. Задача проектировщика линии связи – необходимо выбрать высоты антенн h1 и h2 на холмах І и ІV такими, чтобы: а) «просвет» между АВ и вершинами ІІ и ІІІ холмов был не меньше, чем радиус первой зоны Френеля, рассчитанный в месте расположения соответствующих холмов; б) чтобы h1 и h2 обеспечивали «чистоту первой зоны Френеля», т.е. «просветы» должны быть больше радиусов Френеля для ІІ и ІІІ холмов. Тогда холмы не будут ослаблять поля волны. 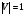 , т.е. поле как в свободном пространстве. , т.е. поле как в свободном пространстве.Значение радиусов Френеля над холмами ІІ и ІІІ 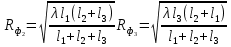 Масштабная сетка для построения профиля трассы На практике определение «просветов» осуществляется более сложно, чем на рисунке ( ), так как необходимо учитывать рельеф местности. Рельеф местности обычно задаётся в виде отметок (высот) над «уровнем моря» (или условный нулевой уровень), т.е. строят профиль трассы. Профиль трассы строится в прямоугольной системе координат, в которой по оси абсцисс отсчитывают расстояние в [км], а по оси ординат – высоты в [м]. Прежде всего наносят линию, изображающую уровень моря или условный нулевой уровень, точки которого определяются по формуле дальности горизонта, имеющая вид в прямоугольной системе (из формулы rпр вид = 3,57( 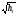 + +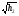 )) ))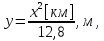 где х – протяжённость трассы. Это уравнение параболы. Масштабная сетка: 1) высоты наносятся по вертикали, а не по нормалям к поверхности земли; 2) линии одинаковых высот повторяют параболическую форму Земли. Расстояние между смежными кривыми одинаково. Для удобства приходится искусственно растягивать масштаб высот. На профиле трассы наносят лес, местные предметы (строения и т.д.), пользуясь топографическими картами (рис. ). Зная высоту подъёма передающей и приёмной антенн, на профиле трассы проводят линию АВ, соединяющую точки расположения передатчика и приёмника. 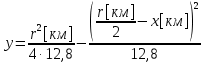 , ( ) , ( )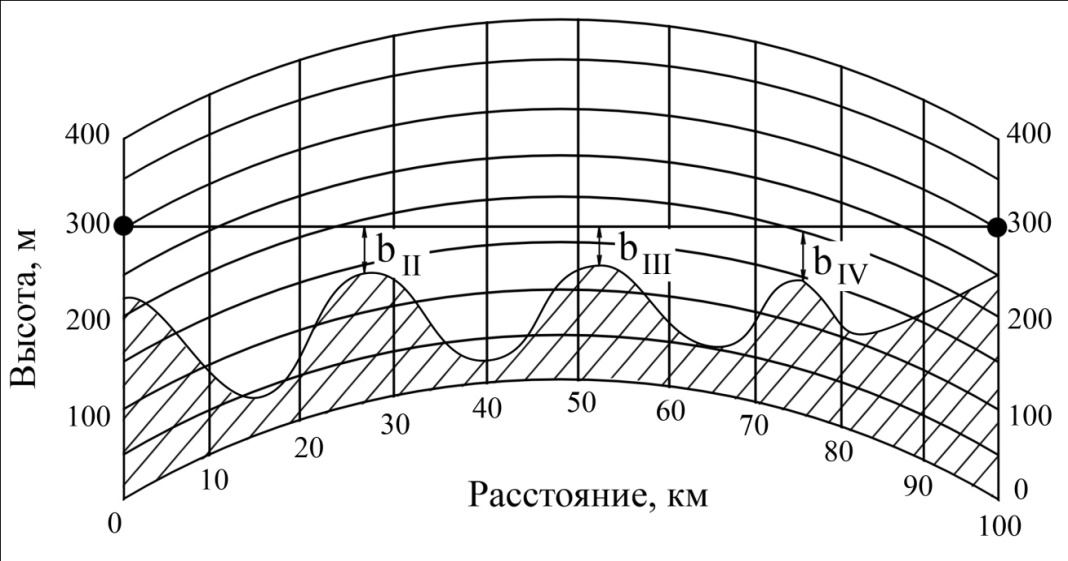 Рисунок – Определение необходимых высот антенн по профилю земной поверхности, нанесенному на масштабную сетку На рисунке (1) координаты 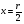 - середина трассы или место нахождения вершины параболы; - середина трассы или место нахождения вершины параболы;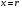 - общая длина трассы; - общая длина трассы;r1 – расстояние от левого конца трассы до точки, в которой определяют величины y. Вводится нормированный коэффициент 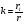 - это относительная координата препятствия, или относительная координата точки отражения. - это относительная координата препятствия, или относительная координата точки отражения. Для расчёта напряжённости поля с учётом влияния рельефа удобно пользоваться не высотами антенн h1 и h2, а величиной просвета между линией АВ и профилем трассы. Величину просвета в наиболее высокой точке профиля трассы обозначим Н, будем считать её положительной, когда линия АВ проходит выше наиболее высокой точки профиля и отрицательной, когда АВ пересекает профиль трассы. Если наиболее высокая часть профиля покрыта лесом, то величина «просвета» определяется относительно верхушек деревьев, т. к. лес на УКВ – непрозрачное препятствие. В зависимости от величины Н в наиболее высокой точке профиля разделяют трассы на открытые, полуоткрытые и закрытые. Величина просвета в этом случае будет сравниваться с величиной Н0, при которой модуль множителя ослабления 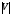 примерно равен 1, если Н = Н0: примерно равен 1, если Н = Н0: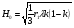 , ( ) , ( )- открытая трасса 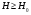 ; ; - полуоткрытая 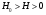 ; ; - закрытая 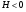 . . Данная классификация приемлема без учёта рефракции. Расчёт напряжённости поля в точке приёма с учётом сферичности Земли в случае холмистой местности Если расстояние между передатчиком и приёмником меньше расстояния прямой видимости, то влияние кривизны земной поверхности становится существенным и его надо учитывать. Влияние кривизны:
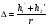 ; ;
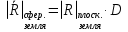 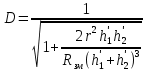 , ( ) , ( )где r – длина трассы; 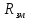 = 6370 км. = 6370 км.При r стремящимся к 0, коэффициента расходимости D стремиться к 1. Открытая трасса ( 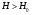 ) – большой положительный просвет. ) – большой положительный просвет. В точку приёма приходят две волны: прямая и отражённая от препятствия (рис. ). 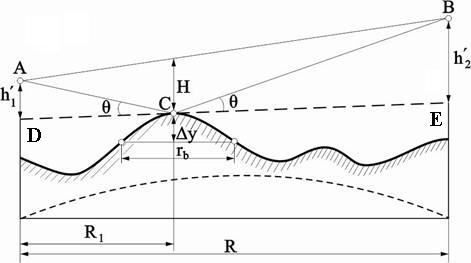 Рисунок - К расчету множителя ослабления на трассах с большим положительным просветом Н Наклон линии АВ незначительный и поэтому ΔACD и ΔCBE – прямоугольные. При этом расстояние АВ можно считать равным протяженности трассы r. На рисунке () введены обозначения: h1’ и h2’ – приведенные высоты; rb – хорда окружности радиуса b; Δу – высота сегмента; b – радиус кривизны сферы, аппроксимирующий препятствие. Необходимо рассчитать Δr, Δ, D, h1’, h2’ через параметры Н и обобщённую координату 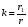 препятствия: препятствия:
Величину b можно рассчитать по значениям Δу и rв, которые определяются из профиля трассы графически. Известно, что высота Δу сегмента окружности радиуса b, хорда которого равна rв при rв << b определяется по формуле: 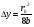 , ,отсюда 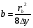 () ()Подставив значение b в выражение для D получим: 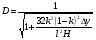 , () , ()где 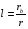 . .Интерференционные минимумы и максимумы с учётом холмистости Т. к. Δ углы скольжения в реальных условиях малы, то:
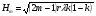 , m = 1, 2, 3 … , m = 1, 2, 3 …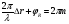 , m = 1, 2, 3 … , m = 1, 2, 3 …
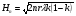 , n = 1, 2, 3 …, и , n = 1, 2, 3 …, и 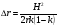
При расчётах удобно иногда пользоваться не абсолютной, а относительной величиной просвета 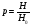 , () , ()откуда 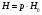 Разность хода лучей Δr (),преобразуем через координату р 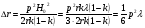 () ()Известно, что 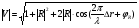 , , тогда с учётом полученного Δr () и, учитывая, что φR = 1800 , множитель 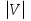 , будет равен , будет равен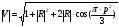 Из этой формулы следует, что интерференционные минимумы и максимумы будут при 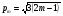 , m = 1, 2, 3 … , m = 1, 2, 3 …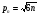 , n = 1, 2, 3 … , n = 1, 2, 3 …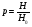 - относительная величина просвета. - относительная величина просвета.Для малых углов скольжения в реальных условиях: 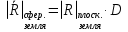 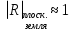 поэтому поэтому 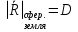 Тогда значения модуля множителя ослабления в интерференционных минимумах 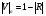 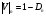 , ,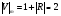 , ,где 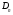 - значение коэффициента расходимости для n-ого минимума. - значение коэффициента расходимости для n-ого минимума.Учитывая, что 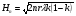 , из формулы , из формулы 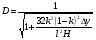 определим 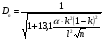 . . Следовательно, 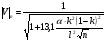 , () , ()где 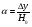 , а , а 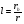 Когда второе слагаемое в 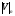 существенно меньше 1, то будут наблюдаться глубокие интерференционные минимумы. Для этого случая существенно меньше 1, то будут наблюдаться глубокие интерференционные минимумы. Для этого случая 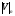 рассчитывается приближённо рассчитывается приближённо 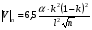 () ()В разделе при изучении отражения от плоской земли было выяснено, что величина модуля множителя ослабления в минимумах очень критична к величине модуля коэффициента отражения. Поэтому, если имеются неровности вблизи геометрической точки отражения, то следует проверять на удовлетворение критерию Рэлея. Критерий Рэлея для n-ого интерференционного минимума принимает вид 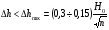 , () , ()где 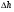 - высота неровностей в минимальной зоне. Если неравенство удовлетворяется, то неровности не играют существенной роли и глубина минимумов будет близка к значениям, рассчитанным по формулам ( ) для - высота неровностей в минимальной зоне. Если неравенство удовлетворяется, то неровности не играют существенной роли и глубина минимумов будет близка к значениям, рассчитанным по формулам ( ) для 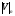 . . Критерий Рэлея проверяется для неровностей, расположенных в пределах минимальной зоны отражающей поверхности. Размеры осей эллипса равны: 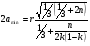 - большая ось - большая ось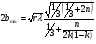 - малая ось - малая осьЕсли точка отражения лежит в середине трассы (k = 0,5), то 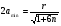 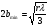 , n = 1, 2, 3 … , n = 1, 2, 3 …При 0 |

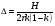 ; ()
; ()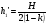 ;
; 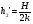 . ()
. ()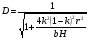 ()
()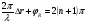 , n = 1, 2, 3 …
, n = 1, 2, 3 …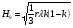 , т. е.
, т. е.