1. Цель и задачи курса теории механизмов и машин. Теория механизмов и машин

• Название: 1. Цель и задачи курса теории механизмов и машин. Теория механизмов и машин
• Дата: 09.03.2018
• Размер: 0.77 Mb.
• Имя файла: TMM.docx
• Тип: Документы; #38026
• страница: 1 из 5

1. Цель и задачи курса теории механизмов и машин.

Теория механизмов и машин - научная дисциплина (или раздел науки), которая изучает строение (структуру), кинематику и динамику механизмов в связи с их анализом и синтезом.

Цель ТММ - анализ и синтез типовых механизмов и их систем. Анализ механизма состоит в исследовании характеристик заданного механизма, например, снятие кинематических характеристик при различных режимах работы. Синтез состоит в определении структуры механизма или количественных параметров схемы механизма при заданных выходных характеристиках, например, проектирование кинематической схемы передачи по заданному передаточному отношению.

Задачи ТММ: разработка общих методов исследования структуры, геометрии, кинематики и динамики типовых механизмов и их систем

2. Машины и их классификация.

Машина - техническое устройство, выполняющее преобразование энергии, материалов и информации с целью облегчения физического и умственного труда человека, повышения его качества и производительности.

Существуют следующие виды машин:

1. Энергетические машины - преобразующие энергию одного вида в энергию

другого вида. Эти машины бывают двух разновидностей:

- Двигатели - преобразуют любой вид энергии в механическую

(например, электродвигатели преобразуют электрическую энергию, двигатели внутреннего сгорания преобразуют энергию расширения газов при сгорании в цилиндре).

- Генераторы - преобразуют механическую энергию в энергию

другого вида (например, электрогенератор преобразует механическую энергию паровой или гидравлической турбины в электрическую).

2. Рабочие машины – машины, использующие механическую энергию для совершения работы по перемещению и преобразованию материалов. Эти машины тоже имеют две разновидности:

- Транспортные машины - используют механическую энергию

для изменения положения объекта (его координат).

- Технологические машины - используют механическую энергию для преобразования формы, свойств, размеров и состояния объекта.

3. Информационные машины - машины, предназначенные для обработки и преобразования информации. Они подразделяются на:

- Математические машины - преобразуют входную информацию в математическую модель исследуемого объекта.

- Контрольно-управляющие машины - преобразуют входную информацию (программу) в сигналы управления рабочей или энергетической машиной.

4. Кибернетические машины – машины, управляющие рабочими или

энергетическими машинами, которые способны изменять программу своих действий в зависимости от состояния окружающей среды (т.е. машины, обладающие элементами искусственного интеллекта).

Машинный агрегат - техническая система, состоящая из одной или

нескольких соединенных последовательно или параллельно машин и предназначенная для выполнения каких-либо требуемых функций. Обычно в состав машинного агрегата входят: двигатель, передаточный механизм и рабочая или энергетическая машина. В настоящее время в состав машинного агрегата часто включается контрольно-управляющая или кибернетическая машина. Передаточный механизм в машинном агрегате необходим для согласования механических характеристик двигателя с механическими характеристиками рабочей или энергетической машины.

3 Машинный агрегат

Машинным агрегатом называется техническая система, состоящая из одной или нескольких соединенных последовательно или параллельно машин и предназначенная для выполнения каких-либо требуемых функций. Обычно в состав машинного агрегата входят: двигатель, передаточный механизм (и их может быть несколько или совсем не быть) и рабочая или энергетическая машина. В настоящее время в состав машинного агрегата часто включается контрольно-управляющая или кибернетическая машина. Передаточный механизм в машинном агрегате необходим для согласования механических характеристик двигателя с механическими характеристиками рабочей или энергетической машины.

 

Схема машинного агрегата.

4. Строение механизмов. Основные определения.

Звено - твердое тело или система жестко связанных тел, входящих в состав механизма.

Стойка - звено, которое при исследовании механизма принимается за неподвижное.

Звено, совершающее 2 вращение вокруг неподвижной оси, называется кривошипом. Если звено совершает качательное движение (неполный оборот), то его называют коромыслом. Звено, совершающее возвратно-поступательное движение, - ползун. Звено, совершающее плоское движение - шатун.

Кинематическая пара - подвижное соединение двух звеньев, допускающее их определенное относительное движение.

Элементы кинематических пар считаются недеформируемыми, а связи, накладываемые кинематической парой, являются голономными, стационарными и удерживающими. Важной характеристикой КП является число степеней свободы s, которое оставляет КП в относительном движении соединяемых ею звеньев. Например, если КП оставляет одну степень свободы в относительном движении (s=1), то такую пару называют одноподвижной. Двухподвижная пара оставляет две степени свободы в относительном движении (s=2).

Низшие кинематические пары – те, в которых контакт звеньев осуществляется по плоскости или поверхности. Если у двух звеньев, входящих в пару, можно построить общие поверхности, то такие пары называют низшими (например, во вращательной паре можно построить общий цилиндр, а в поступательной – общую плоскость). В противном случае пару называют высшей: при каждом положении звеньев имеются только общие линии или точки, расположение которых меняется в процессе движения. Высшей кинематической парой моделируется, например, соединение двух зубчатых колес между собой.

Соединив некоторое число звеньев между собой с помощью КП, получим модель, обладающую новыми свойствами – кинематическую цепь. Кинематическая цепь – совокупность звеньев, связанных между собой

кинематическими парами. Она характеризуется числом степеней подвижности или, иначе говоря, числом двигателей, которые надо подсоединить к цепи для того, чтобы полностью определить положение всех звеньев цепи.

Общее число степеней подвижности N звеньев, не связанных между собой, равно 6N, однако каждая s-подвижная КП отнимает 6-s степеней подвижности: 1-подвижная КП – пять, 2-х подвижная – четыре и т.д. Таким образом, у кинематической цепи остается число степеней подвижности Wц:

, где рs – число s-подвижных кинематических пар в цепи.

Кинематическая цепь, в которой одно из звеньев принято за неподвижное,

называется механизмом. Поскольку неподвижное звено не обладает подвижностью, для определения числа степеней подвижности механизма W это звено нужно вычесть из числа N:

Это формула Малышева.

Нормальный механизм - такой, в котором число входов совпадает с числом степеней подвижности.

Структурная группа – кинематическая цепь, в которой число входов равно числу степеней подвижности. Частным случаем структурной группы является группа, получившая название группы Ассура, в которой число степеней подвижности равно нулю.

5. Классификация механизмов

В простейшей интерпретации: механизм – это кинематическая цепь + двигатель. Так как механизм состоит из кинематических цепей, то также как и кинематические цепи, механизмы делятся на плоские и пространственные, простые и сложные.

Плоские механизмы – такие, все звенья которых движутся в одной или параллельных плоскостях.

Пространственные механизмы – такие, все звенья которых описывают пространственные кривые.

Простой – механизм, состоящий не более чем из четырех звеньев.

Сложный – механизм, состоящий из более чем четырех звеньев.

Также все механизмы классифицируют по конструктивной схожести.

Ø Рычажные– это механизмы, звенья которых при соединении образуют между собой только низшие кинематические пары. Они применяются для преобразования движения или передачи силы в машинах.

а)

б)

в)

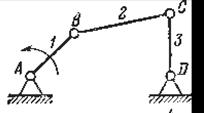
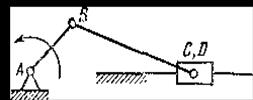
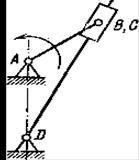
а - коромысловый; б - кривошипно-ползунный; в – кулисный

Рисунок 1.6 - Типовые (частные) рычажные механизмы

Ø Зубчатые механизмы. Если в состав механизма входят зубчатые звенья, то такой механизм называется зубчатым.

Ø Кулачковые механизмы. Механизмы, в состав которых входит звено, имеющее переменный профиль (кулачок), называют кулачковыми.

Ø Фрикционные механизмы – такие механизмы, в которых передача движения между соприкасающимися телами осуществляется за счет сил трения. Ø Механизмы с гибкими звеньями. В таких механизмах в качестве гибких звеньев, передающих движение от одного тела к другому, используются различной формы поперечного сечения ремни, канаты, цепи и др.

Ø Клиновые механизмыприменяются в различного вида зажимных приспособлениях или в устройствах, в которых требуется создать большие усилия на выходной стороне при ограниченных силах, действующих на входной стороне.

Ø Резьбовые (винтовые) механизмы. Механизмы, имеющие в своем составе кинематическую пару «винт-гайка», называют резьбовыми. Резьбовые механизмы применяются для преобразования вращательного движения в поступательное.

Ø Гидравлические и пневматические механизмы подробно рассматриваются при изучении других предметов.

Широкое применение нашли комбинированные механизмы, например рычажно-зубчатые, кулачково-зубчатые и др.

6 классификация кинематических пар

Кинематическая пара – соединение двух твердых тел механизма, допускающее их заданное относительное движение. Условием существования пары является: наличие двух звеньев, их контакт и относительное движение звеньев.

Классификация кинематических пар

1. В зависимости от числа Н различают одно-, двух-, трех-, четырех-, и пятиподвижные кинематические пары. Число уравнений связей принимают за номер класса.

2. По характеру соприкосновения элементов звеньев (точнее виду элементов) пары делят на низшие и высшие  К низшим относят кинематические пары, элементами которых являются поверхности Элементами высших пар являются линии или точки.

3. По характеру сопряжения различают кинематические пары с силовым замыканием (соприкосновение звеньев обеспечивается действием какой - либо силы, например, веса или пружины) и кинематическим (постоянный контакт звеньев достигается за счет конструктивной формы элементов).

4. В зависимости от характера относительного движения звеньев кинематические пары подразделяют на поступательные, вращательные, винтовые, цилиндрические, сферические, плоскостные.

Пара одноподвижная:

1) Вращательная – цилиндрический шарнир. Наложено пять условий связи: исключены все движения, кроме вращательного.

2) Поступательная  – наложено пять условий связи: исключены все движения, кроме одного поступательного.

3) Винтовая – наложено пять условии связи: исключены все движения, кроме поступательного. (Вращение не вносит степени свободы, т.к. в данном случае поступательное и вращательное движения не независимы).

7. Примеры механизмов с низшими парами.

Низшие кинематические пары – те, в которых контакт звеньев осуществляется по плоскости или поверхности (пары скольжения).

Низшие кинематические пары наиболее часто применяются на практике и имеют более простое внутреннее строение, по сравнению с высшими парами. Элемент низшей кинематической пары представляет собой две скользящие друг по другу поверхности, что, с одной стороны распределяет нагрузку в этом элементе, а с другой стороны увеличивает трение при относительном движении звеньев. В связи с этим, использование низших кинематических пар позволяет передавать значительную нагрузку от одного звена на другое, благодаря именно тому, что в этих парах звенья соприкасаются по поверхности.

К низшим парам относятся: 1) вращательная, 2) поступательная, 3) винтовая, 4) цилиндрическая, 5) сферическая, 6) сферическая с пальцем, 7) плоская.

Вращательная пара – одноподвижная, допускает лишь относительное вращательное движение звеньев вокруг оси. Звенья пары соприкасаются по цилиндрической поверхности, следовательно, это низшая пара, замкнутая геометрически. Роль такой кинематической пары выполняет и более сложная конструкция – шарикоподшипник.

Поступательная пара – одноподвижная, с геометрическим замыканием, низшая, допускает лишь прямолинейное поступательное относительное движение звеньев.

Винтовая пара – одноподвижная, с геометрическим замыканием, низшая, допускает относительное винтовое движение звеньев с постоянным шагом. Угловые и линейные перемещения звеньев винтовой пары имею однозначное соответствие, в результате чего остаётся только одна степень подвижности.

Цилиндрическая пара – двухподвижная, с геометрическим замыканием, низшая, допускает независимое вращательное и поступательное относительное движение звеньев.

Сферическая пара – трёхподвижная, с геометрическим замыканием, низшая, допускает три независимых относительных вращения звеньев вокруг осей x, y, z.

Сферическая пара с пальцем – двухподвижная, с геометрическим замыканием, низшая, допускает два независимых относительных вращения звеньев вокруг осей, определяемых прорезью и пальцем (добавленным к сферической паре).

Плоскостная пара - использует силовое замыкание. Эта пара практически не применяется в реальных механизмах.

8. Примеры механизмов с высшими парами

Высшие кинематические пары -это кинематические пары, в которых контакт звеньев, их образующих, осуществляется по линии или в точке;При этом любая высшая кинематическая пара может быть заменена низшей кинематической парой



9. Структурные формулы механизмов.

Основные структурные формулы были составлены для плоских механизмов Чебышевым П.Л. и Грюблером М., для пространственных - Сомовым П.О. и Малышевым.

Формула П. Л. Чебышева для плоских механизмов.

Для плоского механизма используется формула Чебышева:

W = 3n - 1P₄ - 2P₅

где n-число подвижных звеньев

P₄,P₅ - кинематические пары с одной и с двумя наложенными связями.

По-другому эту формулу можно записать в следующем виде:

W = 3n - 2Pн - Pв

где n – общее число подвижных звеньев механизма

Рн – число низших кинематических пар

Рв — число высших кинематических пар

Формула А. П. Малышева для пространственных механизмов.

Важнейшей характеристикой кинематической цепи является число степеней свободы.

Пусть кинематическая цепь содержит n звеньев. До того как они были соединены посредством кинематических пар, система из n звеньев имела 6n степеней свободы. Каждая кинематическая пара m класса дает m уравнений связей относительно координат. Разность между числом степеней свободы и числом уравнений связей дает число независимых координат - степеней подвижности механизма:

W = 6n - 1P₁ - 2P₂ - 3P₃ - 4P₄ - 5P₅.

где n - число подвижных звеньев;

6n- общее число степеней свободы всех звеньев;

P₁, P₂, P₃, Р₄, P₅ — число кинематических пар от 1 до 5 класса;

W- степень подвижности механизма.

10. Механизмы с избыточными степенями свободы

Механизм может содержать такие связи и местные подвижности, которые не влияют на кинематику механизма.

Степень свободы называют лишней, если местная подвижность звена, входящего в механизм, не влияет на кинематику механизма.

Избыточные связи и лишние степени свободы необходимы в реальных механизмах (увеличение жесткости звеньев, уменьшение их износа и так далее). В то же время, избыточные связи могут быть и вредны. Отыскание и устранение избыточных связей обычно неоднозначно и требует специального анализа механизма

В механизмах могут быть лишние степени свободы, не влияющие на закон движения выходного звена и перемещения звеньев. Эти лишние степени свободы определяют лишь возможность существования в механизме некоторых дополнительных движений, не связанных с основным его назначением.  

Как пример кулачковый механизм с двумя роликами

Механизм обладает лишними степенями свободы. Этим лишним степеням свободы соответствует возможность вращения роликов 3 и 5 вокруг осей С и. В самом деле, устранив возможность такого вращения, например жестко скрепив для этого ролики 3 и 5 с рычагом 4, мы не изменим общего характера движения механизма в целом. Поэтому два звена - ролики 3 и 5 - могут быть устранены как особые звенья.

11. Механизмы с «лишними» степенями подвижности.

Иногда при определенных длинах звеньев, наборе кинематических пар и их взаимном расположении одна или несколько кинематических пар отнимают у какого либо звена движение. В этом случае имеет место избыточная или повторная связь.

В общее число наложенных связей может войти некоторое число q избыточных (повторных) связей, которые дублируют другие связи, не уменьшая подвижности механизма, а только обращая его в статически неопределимую систему.

При q=0 механизм – статически определимая система, при q>0 – статически неопределимая система.

Формула Малышева

W = 6n - 1P₁ - 2P₂ - 3P₃ - 4P₄ - 5P₅ + q

Формула Чебышева

W= 3n-2Pн-Pв+q

При определении W необходимо учитывать возможность наличия так называемых «пассивных» звеньев, т.е. звеньев, устраняемых без формального ущерба для кинематики анализируемого механизма.

а) W = 3·4 - 2·6 – 0 = 0 — с пассивным звеном,

б) W = 3·3 - 2·4 – 0 = 1 — фактически.

Если избыточных связей нет (q=0), сборка механизма происходит без деформирования звеньев, последние как бы самоустанавливаются; поэтому такие механизмы называют самоустанавливающимися. Если избыточные связи есть, то сборка механизма и движение его звеньев становится возможным только при деформировании последних.

Когда в механизм вводятся дополнительные звенья, имеющие собственную свободу движения, тогда говорят о лишней степени свободы.

12. Плоские группы Ассура.

Плоский механизм – механизм, все точки звеньев которого описывают траектории, лежащие в параллельных плоскостях. К плоскому механизму относятся зубчатые и фрикционные механизмы для передачи вращения между параллельными осями, плоские механизмы с вращательными и поступательными парами.

Эта модель используется достаточно часто. Для таких моделей для определения числа степеней подвижности удобно пользоваться формулой Чебышева: Wп=3(N-1)-2pн-рв

Здесь N – число звеньев механизма, рн – число низших кинематических пар, рв – число высших кинематических пар.

Вывод этой формулы достаточно очевиден: в плоскости движения звенья обладают тремя степенями подвижности; каждая низшая пара отнимает у звеньев по две степени подвижности, оставляя по одной; каждая высшая пара отнимает, соответственно, по одной степени подвижности.

В плоских механизмах, также как и в пространственных, можно выделить

структурные группы; число степеней подвижности плоских структурных групп Wпг находится по формуле:

Wпг=3N-2pн-pв

Если Wпг=0, то такая структурная группа называется плоской группой Ассура.

Возможные плоские группы Ассура:

1) N=1, тогда рн=1 и рв=1

2) Если N=2 (такую группу Ассура называют диадой), тогда рн=3, рв=0, то есть в двухзвенной группе Ассура должны быть три низшие кинематические пары. Это могут быть вращательные или поступательные КП в различных сочетаниях.

3) Если N=3, то в группе Ассура могут быть четыре низшие КП и одна высшая (рн=4, рв=1, Wпг=3×3-2×4-1=0), либо три низших и три высших КП (Wпг=3×3-2×3-3=0), либо две низших и пять высших (Wпг=3×3-2×2-5=0).

13. Структурный анализ плоских рычажных механизмов.

При проведении теоретических и экспериментальных исследований пользуются различными расчетными схемами и моделями механизмов и машин. Они обычно отражают только те свойства механизмов и машин, которые существенно влияют на исследуемые характеристики. Так, при анализе структуры механизма используют его структурную схему; при анализе кинематики — кинематическую; динамики — динамическую. Структурная схема механизма должна содержать информацию о числе его звеньев и их взаимном расположении, виде расположении и классе (или числе подвижностей) кинематических пар.

Основные понятия структурного анализа: