линейная алгебра. дззз. 1. Матрицы Основные понятия
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
1. Матрицы 1.1. Основные понятия Матрицейназывается прямоугольная таблица, содержащая м-строк или н-столбцов, одинаковой длины . Величины, составляющие матрицу, называются ее элементами. Матрица, имеющая одинаковое количество строк и столбцов, называется квадратной. Для квадратной матрицы число m = n называется ее порядком (Единичная)Матрица, каждый элемент главной диагонали которой равен единице, а все остальные — нулю. 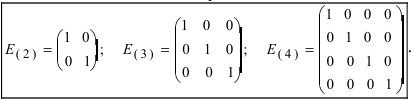 Квадратная матрица называется диагональной, если все ее элементы, находящиеся вне главной диагонали, равны нулю, то есть aij = 0 при всех i≠j  Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной  Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы - на соответствующие строки. 1.2. Действия над матрицами Суммой (разностью) двух матриц При умножении вещественного числа k на матрицу Произведением матриц А и В называется матрица С, элементы которой вычисляются по формуле 2. Определители 2.1. Основные понятия Определителем порядка n называется число (выражение), записанное в виде квадратной таблицы, имеющей n строк и n столбцов, которая раскрывается по определенному правилу. Определителем матрицы второго порядка Пусть дана квадратная матрица третьего порядка: Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (1.4), легко запомнить, пользуясь схемой (рис. 1.1), которая называется правилом треугольников  2.2. Свойства определителей Определитель треугольной матрицы равен произведению элементов главной диагонали. При транспонировании матрицы ее определитель не изменяется. От перестановки двух рядов (строк или столбцов) определитель меняет знак. Общий множитель всех элементов некоторого ряда определителя можно выносить за знак определителя. Если все элементы какого-нибудь ряда матрицы равны нулю, то определитель равен нулю. Определитель, содержащий два пропорциональных ряда, равен нулю. Определитель не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы другого ряда, умноженные на одно и то же число. Определитель произведения двух матриц одинакового порядка равен произведению определителей этих матриц. Целью таких преобразований является приведение определителя к треугольному виду, что решает проблему его вычисления. Минор матрицы - это определитель −1 порядка, составленный путём вычеркивания ii-ой строки и jj-го столбца из матрицы A порядка n. Обозначается минор Mij. По определению каждый минор Mij равен определителю, получаемому при вычеркивании ii-ой строки и jj-ого столбца из матрицы A. Алгебраическим дополнением Aij к элементу aij определителя n-го порядка называется число Aij = (-1)i + j · Mij Теорема разложения. Выберем i,j-ый элемент этой матрицы и вычеркнем i-ую строку и j-ый столбец. В результате мы получаем матрицу (n – 1)-го порядка, определитель которой называется минором элемента и обозначается символом Mi j Определитель матрицы равен сумме произведений элементов любого ряда на их алгебраические дополнения. Пример №2 Вычислить определитель, разлагая его по элементам первой строки: 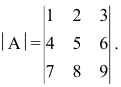 Решение: По теореме разложения Найдем алгебраические дополнения элементов матрицы А: 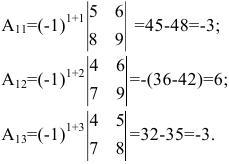 Следовательно, 3. Невырожденные матрицы Квадратная матрица Матрицей, союзной к матрице  где Матрица где Составим алгоритм нахождения обратной матрицы с использованием равенства Вычисляем определитель матрицы А и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима). Строим Транспонируем матрицу Умножаем каждый элемент матрицы Проводим проверку результата, вычисляя произведения Рангомматрицы Ранг матрицы Из определения следует: а) ранг матрицы б) в) для квадратной матрицы 4. Системы линейных алгебраических уравнений (СЛАУ) 4.1. Основные понятия Будем рассматривать системы из p линейных алгебраических уравнений с n неизвестными переменными (p может быть равно n) вида 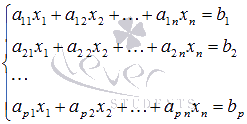 Такую форму записи СЛАУ называют координатной. В матричной форме записи эта система уравнений имеет вид где  - основная матрица системы, - основная матрица системы, 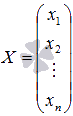 - матрица-столбец неизвестных переменных, - матрица-столбец неизвестных переменных, 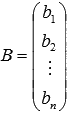 - матрица-столбец свободных членов. - матрица-столбец свободных членов.Если к матрице А добавить в качестве (n+1)-ого столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу системы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т, а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,  Решением системы линейных алгебраических уравнений называют набор значений неизвестных переменных Если система уравнений имеет хотя бы одно решение, то она называется совместной. Если система уравнений решений не имеет, то она называется несовместной. Если СЛАУ имеет единственное решение, то ее называют определенной; если решений больше одного, то – неопределенной. Если свободные члены всех уравнений системы равны нулю 4.2. Решение СЛАУ. Теорема Кронекера-Капелли Теорема Кронекера – Капелли. ТЕОРЕМА 1 (Кронекера – Капелли). Система линейных уравнений (1) совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу ее расширенной матрицы, т.е. r(A) = r(A*). ТЕОРЕМА 2 (критерий единственности решения). Система линейных уравнений (1) имеет единственное решение тогда и только тогда, когда ранг основной матрицы системы равен рангу ее расширенной матрицы и равен числу переменных, т.е. r(A) = r(A*) = n.  4.3. Решение невырожденных СЛАУ Метод Крамера Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение 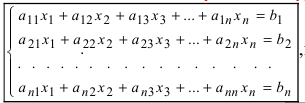 Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы  Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 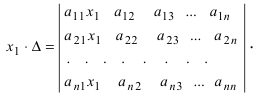 Второй столбец умножим на 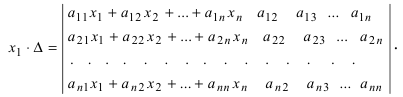 Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е. 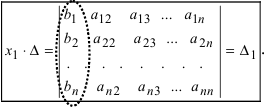 Определение: Определитель Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:  31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов. Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 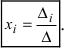 Проанализируем полученные формулы: Проанализируем полученные формулы:если главный определитель системы отличен от нуля ( если главный определитель системы равен нулю ( если все определители системы равны нулю ( Пример: Решить СЛАУ методом Крамера 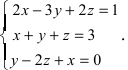 Решение: Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом 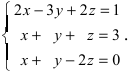 Найдем главный определитель СЛАУ (раскрываем по первой строке) 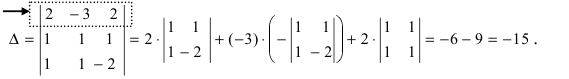 Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя 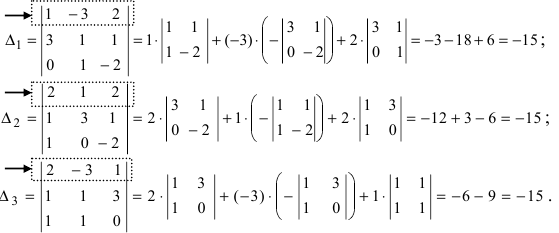 Воспользуемся формулами Крамера Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений. Выполним проверку 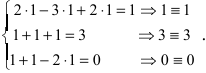 Отсюда видно, что СЛАУ решена верно. Отсюда видно, что СЛАУ решена верно.Заказать решение задач по высшей математике Матричный способ решения СЛАУ Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных  матpицы-столбцы неизвестных матpицы-столбцы неизвестных 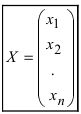 и свободных коэффициентов и свободных коэффициентов  Тогда СЛАУ можно записать в матричном виде Пример: Решить СЛАУ матричным способом 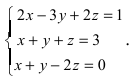 Решение: Введем в рассмотрение следующие матрицы 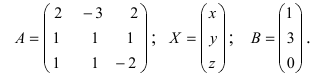 Найдем матрицу Пример: Решение: Найдем алгебраические дополнения всех элементов 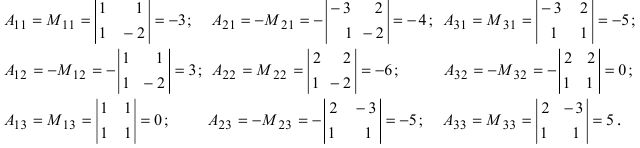 Запишем обратную матрицу Запишем обратную матрицу 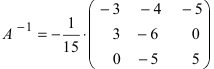 (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В: (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В: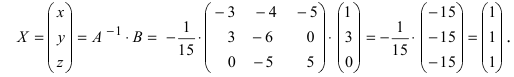 Отсюда находим, что х = 1; y = l; z = l. 4.4. Метод Гаусса. Метод Гаусса Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции Прямой ход метода Гаусса Сначала запишем расширенную матрицу системы. Для этого в главную матрицу добавляем столбец свободных членов. 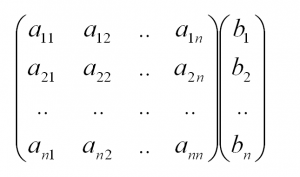 Вся суть метода Гаусса заключается в том, чтобы путем элементарных преобразований привести данную матрицу к ступенчатому (или как еще говорят треугольному) виду. В таком виде под (или над) главной диагональю матрицы должны быть одни нули. 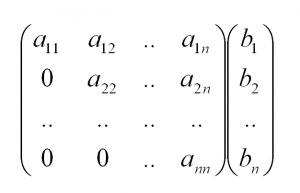 Что можно делать: Можно переставлять строки матрицы местами; Если в матрице есть одинаковые (или пропорциональные) строки, можно удалить их все, кроме одной; Можно умножать или делить строку на любое число (кроме нуля); Нулевые строки удаляются; Можно прибавлять к строке строку, умноженную на число, отличное от нуля. Обратный ход метода Гаусса После того как мы преобразуем систему таким образом, одна неизвестная Xn становится известна, и можно в обратном порядке найти все оставшиеся неизвестные, подставляя уже известные иксы в уравнения системы, вплоть до первого. Когда интернет всегда под рукой, можно решить систему уравнений методом Гаусса онлайн. Достаточно лишь вбить в онлайн-калькулятор коэффициенты. Но согласитесь, гораздо приятнее осознавать, что пример решен не компьютерной программой, а Вашим собственным мозгом. Пример решения системы уравнений методом Гаусс А теперь — пример, чтобы все стало наглядно и понятно. Пусть дана система линейных уравнений, и нужно решить ее методом Гаусса: 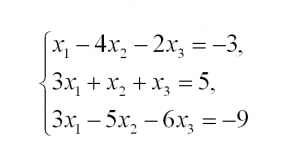 Сначала запишем расширенную матрицу: 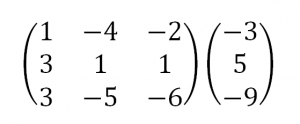 Теперь займемся преобразованиями. Помним, что нам нужно добиться треугольного вида матрицы. Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой и получим: 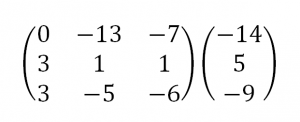 Затем умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой: 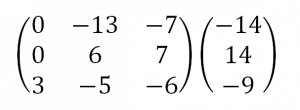 Умножим 1-ую строку на (6). Умножим 2-ую строку на (13). Добавим 2-ую строку к 1-ой: 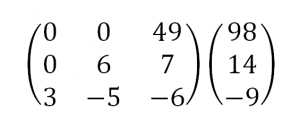 Вуаля — система приведена к соответствующему виду. Осталось найти неизвестные: 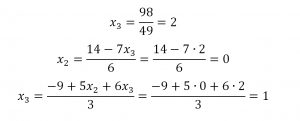 Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах. Следствия из теоремы Кронекера - Капелли Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная). Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная). В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы. 4.5. Системы линейных однородных уравнений (СЛОУ) Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид: 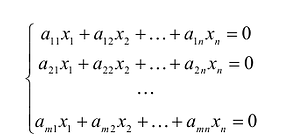 Очевидно, что всякая однородная система совместна и имеет нулевое (тривиальное) решение. Поэтому применительно к однородным системам линейных уравнений часто приходится искать ответ на вопрос о существовании ненулевых решений. Ответ на этот вопрос можно сформулировать в виде следующей теоремы. Теорема. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных.  Теорема 4.4. Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг Необходимость. Так как ранг не может превосходить размера матрицы, то, очевидно, Достаточность. Пусть Пусть дана однородная система 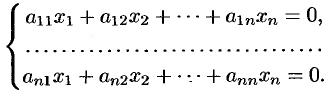 Теорема 4.5. Для того, чтобы однородная система Если система имеет ненулевые решения, то II. Элементы векторной алгебры Основные понятия. Величины, которые полностью определяются своими численным значением, называется скалярными. Примеры: площадь, длина, объем, температура, работа, масса. Другие величины, например, сила скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называются векторными. Определение Вектор – это скаляр, имеющий направление. a.Обозначение: AB, a . Противоположный вектор BA,-а Длиной или модулем вектора называется его скаляр. Обозначение AB , a . Вектор, модуль которого равен 1 называется единичным вектором. Обозначение e. Единичный вектор, который совпадает с направлением вектора a называется ортом ( 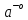 ) )Определение Векторы a и b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых (аIIв) Определение a b , если они аIIв одинаковы направлены и имеют одинаковые длины. Вывод: Вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства Определение a , b, c - компланарные, если они лежат в одной плоскости или параллельных плоскостях   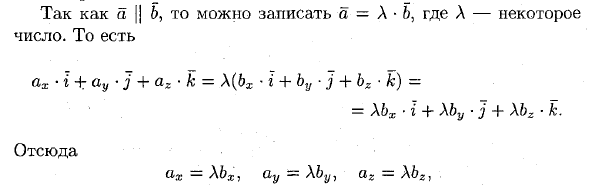  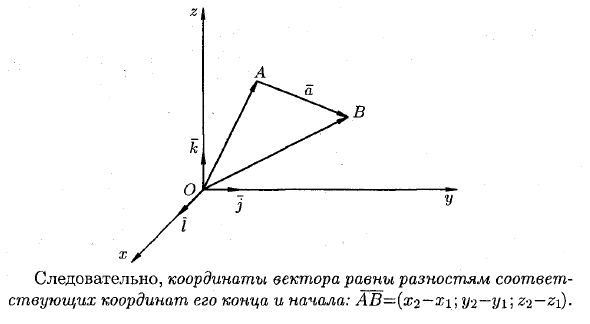 |
