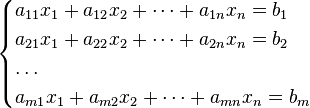Билеты по матану. Матрицей AAmn порядка mn называется прямоугольная таблица чисел, содержащая m строк и n столбцов

Название	Матрицей AAmn порядка mn называется прямоугольная таблица чисел, содержащая m строк и n столбцов
Анкор	Билеты по матану.docx
Дата	02.05.2017
Размер	1.28 Mb.
Формат файла
Имя файла	Билеты по матану.docx
Тип	Документы #6280
страница	1 из 6

1 2 3 4 5 6

1 Матрица

Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.

Элементы матрицы aij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a11, a22,..., ann .

Действия над матрицами.

1. Сложение матриц - поэлементная операция

2. Вычитание матриц - поэлементная операция

3. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

4. Произведение матрицы на число - поэлементная операция

2 Определитель

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры.

Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов.

Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица.

Определитель второго порядка вычислим, например, по элементам первой строки

Запишем разложение данного определителя по элементам второй строки

Полученный результат совпадает с результатом вычисления определителя по первой строке. Этот же результат получится и при разложении по любому из столбцов. Рекомендуем это проверить самостоятельно.

Из сказанного можно заключить, что определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.

Пример

Найдем определитель третьего порядка, раскладывая его по элементам, например, третьего столбца

Пример.

Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Получается, что определитель n - го порядка мы найдем через определители (n -1) - го порядка.

3 Обратная матрица

Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Свойства обратной матрицы

, где обозначает определитель.

для любых двух обратимых матриц

где

обозначает транспонированную матрицу.

для любого коэффициента

.

Первый способ.

1. Вычислить определитель

данной матрицы. Если

, то обратной матрицы не существует (матрица вырожденная).

2. Составить матрицу

из алгебраических дополнений

элементов матрицы 3. Транспонируя матрицу , получить присоединенную матрицу

.

4. Найти обратную матрицу (4.1), разделив все элементы присоединенной матрицы на определитель

Второй способ. Для нахождения обратной матрицы можно использовать элементарные преобразования.(метод гаусса)

1. Составить блочную матрицу

, приписав к данной матрице

единичную матрицу того же порядка.

2. При помощи элементарных преобразований, выполняемых над строками матрицы

, привести ее левый блок

к простейшему виду

. При этом блочная матрица приводится к виду

, где

— квадратная матрица, полученная в результате преобразований из единичной матрицы

.

3. Если

, то блок

равен обратной матрице, т.е.

. Если

, то матрица

не имеет обратной.

В самом деле, при помощи элементарных преобразований строк матрицы

можно привести ее левый блок

к упрощенному виду

(см. рис. 1.5). При этом блочная матрица

преобразуется к виду

, где

— элементарная матрица, удовлетворяющая равенству

. Если матрица

невырожденная, то согласно п.2 замечаний 3.3 ее упрощенный вид совпадает с единичной матрицей

. Тогда из равенства следует, что

. Если же матрица вырожденная, то ее упрощенный вид

отличается от единичной матрицы, а матрица

не имеет обратной.

4 Системы линейных алгебраических уравнений

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

$\begin{cases} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2\\ \dots\\ a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m \\ \end{cases}$

Здесь  — количество уравнений, а  — количество неизвестных. x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными^[1]. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^.Система линейных уравнений может быть представлена в матричной форме как: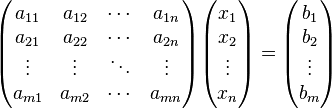

$\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{pmatrix}$

Здесь  — это матрица системы,  — столбец неизвестных, а  — столбец свободных членов. Если к матрице  приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

5 Правило Крамера решения системы линейных уравнений

Метод Крамера

Система линейных уравнений: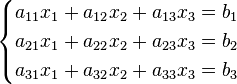

$\begin{cases} a_{11}x_1 + a_{12}x_2 + a_{13}x_3 = b_1\\ a_{21}x_1 + a_{22}x_2 + a_{23}x_3 = b_2\\ a_{31}x_1 + a_{32}x_2 + a_{33}x_3 = b_3\\ \end{cases}$

Определители: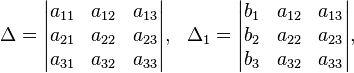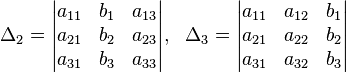

$\delta=\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{vmatrix},\ \ \delta_1=\begin{vmatrix} b_1 & a_{12} & a_{13} \\ b_2 & a_{22} & a_{23} \\ b_3 & a_{32} & a_{33} \\ \end{vmatrix},\ \$

$\delta_2=\begin{vmatrix} a_{11} & b_1 & a_{13} \\ a_{21} & b_2 & a_{23} \\ a_{31} & b_3 & a_{33} \\ \end{vmatrix},\ \ \delta_3=\begin{vmatrix} a_{11} & a_{12} & b_1 \\ a_{21} & a_{22} & b_2 \\ a_{31} & a_{32} & b_3 \\ \end{vmatrix}$

Решение:

$x_1=\frac{\delta_1}{\delta},\ \ x_2=\frac{\delta_2}{\delta},\ \ x_3=\frac{\delta_3}{\delta}$

6 Метод гаусса решения системы линейных уравнений

Ме́тод Га́усса^] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы

Алгоритм решени методом Гаусса подразделяется на два этапа.

На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме.

Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.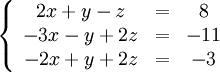

$\left\{\begin{array}{ccc}2x + y - z &=& 8 \\ -3x - y + 2z &=& -11 \\ -2x + y + 2z &=& -3 \end{array}\right.$

Обнулим коэффициенты при  во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на  и , соответственно: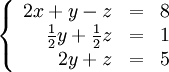

$\left\{\begin{array}{rcc} 2x + y - z &=& 8 \\ \frac{1}{2}y + \frac{1}{2}z &=& 1 \\ 2y + z &=& 5 \end{array}\right.$

Теперь обнулим коэффициент при  в третьей строке, вычтя из неё вторую строку, умноженную на :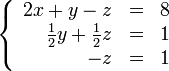

$\left\{\begin{array}{rcc} 2x + y - z &=& 8 \\ \frac{1}{2} y + \frac{1}{2} z &=& 1 \\ -z &=& 1 \\ \end{array}\right.$

В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

из третьего;

из второго, подставив полученное

из первого, подставив полученные  и .

7 Матричный метод

Пусть для матрицы А порядка n на n существует обратная матрица . Умножим обе части матричного уравнения  слева на  (порядки матриц A ⋅ X и В позволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем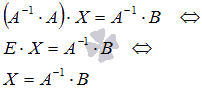

. Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как

, а по определению обратной матрицы (E – единичная матрица порядка n на n), поэтому
формула

Таким образом, решение системы линейных алгебраических уравнений матричным методом определяется по формуле

. Другими словами, решение СЛАУ находится с помощью обратной матрицы .

Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.

8 Декартова и полярная система координат

Декартова система координат на плоскости определяется некоторой ее точкой O и базисом из двух векторов, параллельных плоскости. Точка Oназывается началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. Они лежат в плоскости и называются осями абсцисс и ординат. Каждая ось координат является числовой осью с началом в точке O, положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора.

Координатами точки M называются координаты вектора OM (радиус–вектора) (см. рис. 1).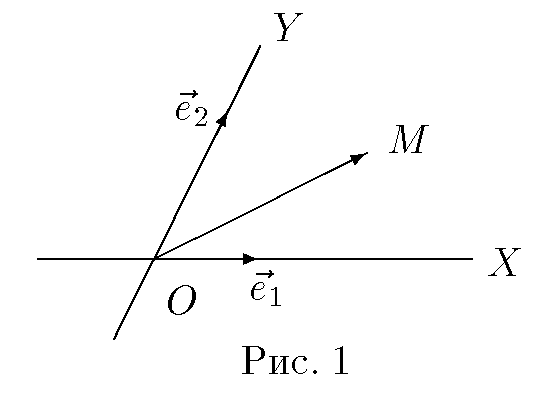

http://www.academiaxxi.ru/www_books/hm/ag/02/01/t1.gif

Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной.

На плоскости часто употребляется также полярная система координат (рис. 2).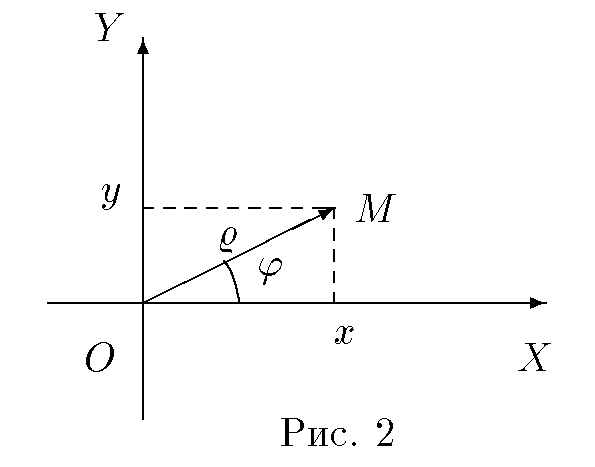

http://www.academiaxxi.ru/www_books/hm/ag/02/01/t2.gif

Она определяется точкой O, называемой полюсом, и лучом, исходящим из полюса, называемым полярной осью. Полярными координатами ρ и j точкиM называются расстояние ρ от полюса до точки M ( ρ = |OM|) и угол j между полярной осью и вектором OM (рис. 2). Угол j называется полярным углом, измеряется в радианах и отсчитывается от полярной оси против часовой стрелки. Полярные координаты точки O: ρ = 0, угол j не определен. У остальных точек ρ > 0 и угол j определен с точностью до 2π. Обычно полагают 0 ≤ j < 2 π или − π < j ≤ π.

Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс, то декартовы координаты x и y точки M выражаются через ее полярные координаты ρ и j формулами

x = ρcosj y = ρsinj .

Полярные координаты ρ и j точки M выражаются через ее декартовы координаты x и y формулами

√

x² + y²

cosj = √ x² + y²

sinj = √ x² + y²

1 2 3 4 5 6