Билеты по матану. Матрицей AAmn порядка mn называется прямоугольная таблица чисел, содержащая m строк и n столбцов
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
|
17 Кривые второго порядка, определения и канонические уравнения Кривые второго порядка – это эллипс, окружность, гипербола и парабола Общим уравнением второго порядка называется уравнение вида: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0 Эллипс – геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек F1,F2 (фокусы) есть величина постоянная, равная 2a. В частном случае, когда a=b (c=0, ε=0, фокусы сливаются в одной точке - центре), эллипс вырождается в окружность. Гипербола - геометрическое место точек, для каждой из которых модуль разности расстояний от нее до двух данных точек F1,F2 (фокусы) есть величина постоянная, равная 2a. Парабола – геометрическое место точек, каждая из которых равноудалена от данной точки (фокус) и от данной прямой (директриса) Канонические уравнения кривых второго порядка окружность радиуса , начало координат – центр симметрии (рис. 11); эллипс, осевая симметрия (рис. 11); 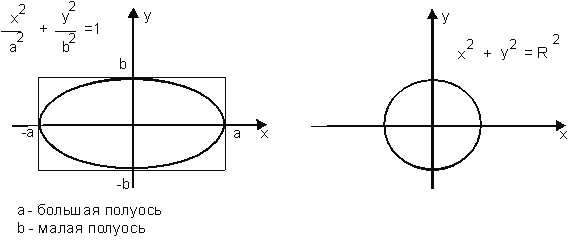 Рис. 11. Эллипс и окружность гипербола, пересекает ось (рис. 12), осевая симметрия; гипербола, пересекает ось (рис. 12), осевая симметрия; 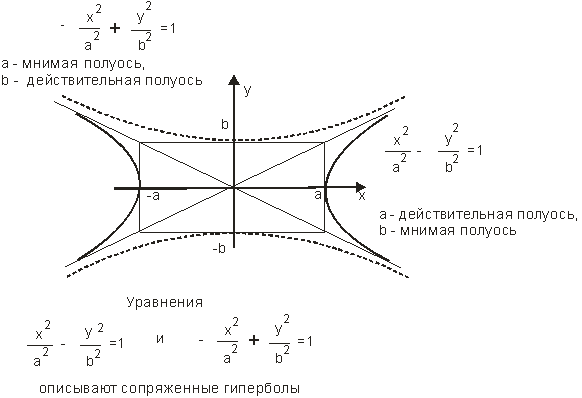 Рис. 12. Сопряженные гиперболы парабола, параметр, вершина в начале координат, ветви направлены вверх, ось ось симметрии (рис. 13); парабола, параметр, вершина в начале координат, ветви направлены вниз, ось ось симметрии (рис. 13); парабола, параметр, вершина в начале координат, ветви направлены вправо, ось ось симметрии (рис. 13) ; парабола, параметр, вершина в начале координат, ветви направлены влево, ось ось симметрии (рис. 13) . 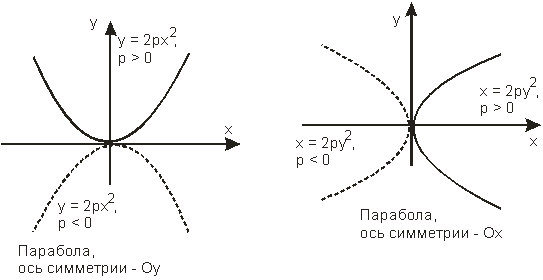 Рис. 13. Параболы 18 поверхности второго порядка К невырожденным поверхностям второго порядка относятся эллипсоид, эллиптический параболоид, гиперболический параболоид, однополостной гиперболоид и двуполостной гиперболоид. Строгое изучение этих поверхностей проводится в курсе аналитической геометрии. Здесь же мы ограничимся определениями и иллюстрациями. Определение Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, c > 0, называется эллипсоидом.
Определение Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, называется эллиптическим параболоидом. Определение Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, называется гиперболическим параболоидом. Определение Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, c > 0, называется однополостным гиперболоидом. Определение Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, c > 0, называется двуполостным гиперболоидом. По аналогии с коническими сечениями существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x2 = 0 описывается пара совпадающих плоскостей, уравнением x2 = 1 – пара параллельных плоскостей, уравнением x2 – y2 = 0 – пара пересекающихся плоскостей. Уравнение x2 + y2 + z2 = 0 описывает точку с координатами (0; 0; 0), уравнение x2 + y2 = 1 – круговой цилиндр, уравнение x2 + y2 = z2 – круговой конус. Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии. 19 Предел функции и его геометр.смысл одностороние пределы Число А называется пределом функции в точке хо (или при х→хо), если для любого положительного ε найдется такое положительное число δ, что для все ххо, удовлетворяющих неравенству |х-хо|<δ, выполняется неравенство |ƒ(х)-А|<ε. 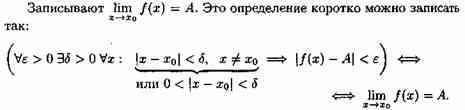 Геометрический смысл предела функции: если для любой ε-окрестности точки А найдется такая δ-окрестность точки хо, что для всех ххо из етой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε). 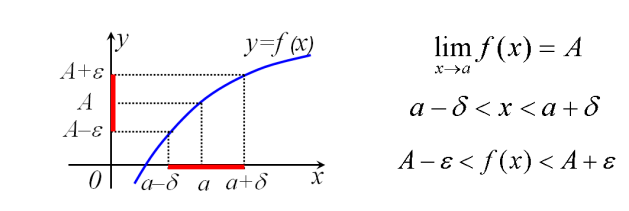 Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами. Число называется правым пределом функции в точке , если для такое, что для любого и , выполняется неравенство Число называется левым пределом функции в точке , если для такое, что для любого и , выполняется неравенство 20 свойствва пределов. Первый и второй замечтльный предел 1° Предел суммы/разности двух функций равен сумме/разности их пределов: 2° Предел произведения двух функций равен произведению их пределов: 3° Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю: 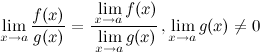 4° Константу можно выносить за знак предела: °5 Предел степени с натуральным показателем равен степени предела: Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны: Первый замечательный предел: Определение Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю. Второй замечательный предел: 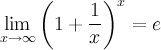 здесь е - число Эйлера. 21 Основные неопределенности пределов и их раскрытие. С непосредственным вычислением пределов основных элементарных функций разобрались. При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называют неопределенностями.  22 бесконечно малые и бесконечно большие функции Функция 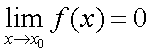 .Аналогично определяются бесконечно малые функции при .Аналогично определяются бесконечно малые функции при Функция 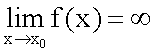 , т.е. функция , т.е. функция 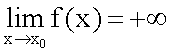 23 Эквивалентно беск.мал. Функции и 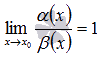 Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы. Таблица эквивалентных бесконечно малых. Пусть - бесконечно малая при .  24 Понятие непрерывности в точке Функция у = f (х) называется непрерывной в точке , если бесконечно малому приращению Δ х аргумента х в точке соответствует бесконечно малое приращение функции Δ y, т. е. Непрерывность функции На практике удобно использовать следующие 3 условия непрерывности функции f (x) в точке x = a :
Определение непрерывности по Коши (нотация Рассмотрим функцию f (x), которая отображает множество действительных чисел выполняется неравенство Точка называется точкой разрыва функции , если она определена в некоторой проколотой окрестности точки (то есть определена на некотором интервале, для которого служит внутренней точкой, но в самой точке , возможно, не определена Устранимые точки разрыва Если предел функции существует, но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке: то точка называется точкой устранимого разрыва функции . |
