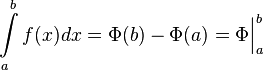Билеты по матану. Матрицей AAmn порядка mn называется прямоугольная таблица чисел, содержащая m строк и n столбцов
 Скачать 1.28 Mb.
|
|
Достаточные условия возрастания и убывания функции. На основании достаточных условий (признаков) возрастания и убывания функции находятся промежутки возрастания и убывания функции. Вот формулировки признаков возрастания и убывания функции на интервале:
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
34 нахождение наибольшего и наименьшего значения функции на отрезке Теорема (Вторая теорема Вейерштрасса): Если функция определена и непрерывна в замкнутом промежутке , то она достигает в этом промежутке своих наибольшего и наименьшего значений. Функция может достигать своих наибольших и наименьших значений либо на внутренних точках промежутка, либо на его границах. Проиллюстрируем все возможные варианты.  Пояснение: 1) Функция достигает своего наибольшего значения на левой границе промежутка в точке , а своего наименьшего значения на правой границе промежутка в точке . 2) Функция достигает своего наибольшего значения в точке (это точка максимума) , а своего наименьшего значения на правой границе промежутка в точке . 3) Функция достигает своего наибольшего значения на левой границе промежутка в точке , а своего наименьшего значения в точке (это точка минимума). 4) Функция постоянна на промежутке, т.е. она достигает своего минимального и максимального значения в любой точке промежутка, причем минимальное и максимальное значения равны между собой. 5) Функция достигает своего наибольшего значения в точке , а своего наименьшего значения точке (несмотря на то, что функция имеет на этом промежутке как максимум, так и минимум). 6) Функция достигает своего наибольшего значения в точке (это точка максимума), а своего наименьшего значения в точке (это точка минимума). Алгоритм решения задачи. 1) Найти производную функции . 2) Найти стационарные точки (и точки, подозрительные на экстремум), решив уравнение . Обратить внимание на точки, в которых не существует двусторонней конечной производной. 3) Вычислить значения функции в стационарных точках и на границах интервала. 4) Выбрать из полученных значений наибольшее (наименьшее) и записать ответ. 35 Выпуклость функции, точки перегиба График функции , дифференцируемой на интервале , является на этом интервале выпуклым, если график этой функции в пределах интервала лежит не выше любой своей касательной (рис. 1). График функции , дифференцируемой на интервале , является на этом интервале вогнутым, если график этой функции в пределах интервала лежит не ниже любой своей касательной (рис. 2). 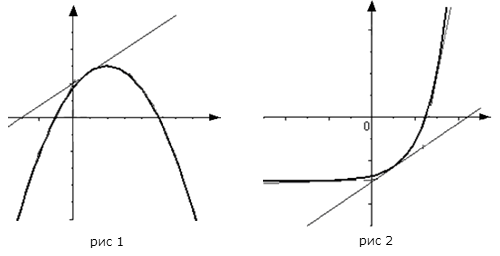 Теорема_(О_необходимом_условии_существования_точки_перегиба)'>Теорема_(Об_условиях_выпуклости_или_вогнутости_графика_функции)'>Теорема (Об условиях выпуклости или вогнутости графика функции) Пусть функция определена на интервале и имеет непрерывную, не равную нулю в точке вторую производную. Тогда, если всюду на интервале , то функция имеетвогнутость на этом интервале, если , то функция имеет выпуклость. Определение Точкой перегиба графика функции называется точка  , разделяющая промежутки выпуклости и вогнутости.Теорема (О необходимом условии существования точки перегиба) Если функция имеет перегиб в точке , то или не существует.Теорема (О достаточном условии существования точки перегиба) Если:
тогда в точке функция имеет перегиб.36 применение второй производной для нахождения интервалов выпуклости Кривая  называется выпуклой вниз (вверх) в промежутке  , если она лежит выше (ниже) касательной в любой точке этого промежутка.Выпуклость кривой, являющейся графиком функции , характеризуется знаком её второй производной: если в некотором промежутке  , то кривая выпукла вниз в этом промежутке; если же  , то кривая выпукла вверх в этом промежутке.Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Если в точке перегиба x0существует вторая производная f ''( x0 ), то  .Теорема. Пусть дифференцируема на промежутке . Если во всех точках промежутка вторая производная функции y=f(x) отрицательная, т.е., то график функции на этом промежутке выпуклый, если же – вогнутый.37 Общая схема исследования функций и построения их графиков При исследовании функций и построении их графиков целесообразно пользоваться следующей схемой. 1. Нахождение области определения функции. 2. Исследование функции на четность и нечетность. 3. Установление области непрерывности функции и точек разрыва. Отыскание вертикальных асимптот. 4. Исследование поведения функции при (если она там определена). Отыскание горизонтальных и наклонных асимптот. 5. Нахождение экстремумов и интервалов монотонности функции. Составление таблицы. 6. Нахождение интервалов выпуклости и вогнутости и точек перегиба графика функции. 7. Нахождение точек пересечения графика функции с осями, интервалов знакопостоянства функции. Составление таблицы. Отыскание дополнительных точек для построения графика. 8. Построение графика функции. 38 Первообраз и их множеств. Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство  для любого х из заданного промежутка.Множество всех первообразных Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство  . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.Определение неопределенного интеграла. Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается  свойства неопределенного интеграла
39 Таблица основных интегралов 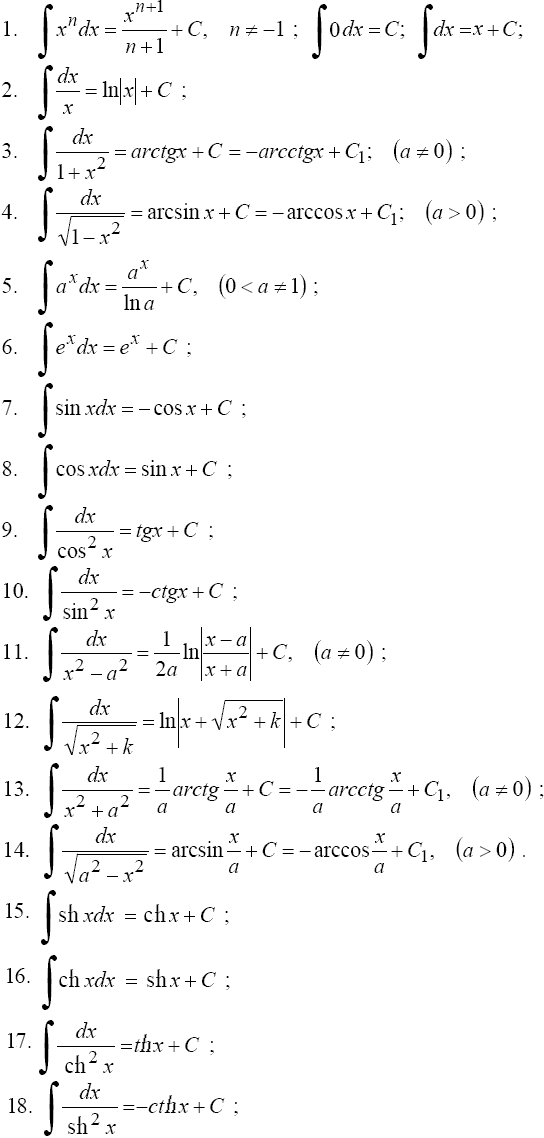 40 Метод непосредственного интегрирования Определение Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. Таким образом, алгоритм действий следующий:
41интегрирование по частям и подставновкой Интегрирование по частям. Если функции u ( x ) и v ( x ) имеют непрерывные первые производные и существует интеграл v ( x ) du ( x ), тосуществует и интеграл u ( x ) dv ( x ) и имеет место равенство: u ( x ) dv ( x ) = u ( x ) • v ( x ) – v ( x ) du ( x ) или в более короткой форме: u dv = u v – v du . Обратите внимание, что интегрирование по частям и дифференциал произведения являются взаимно обратными операциями (проверьте!). Интегрирование подстановкой (замена переменной). Если функция f ( z ) определена и имеет первообразную при z Z, а функция z = g ( x )имеет непрерывную производную при x X и её область значений g ( X ) Z, то функция F ( x ) = f [ g ( x )] × g' ( x ) имеет первообразную на Х и F ( x ) dx = f [ g ( x )] • g' ( x ) dx = f ( z ) dz . 42 определен.интеграл и его определение Определённым интегралом от функции на отрезке называется предел интегральных сумм при стремлении ранга разбиения к нулю , если он существует независимо от разбиения и выбора точек , то есть 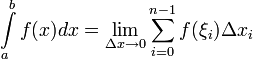 Если существует указанный предел, то функция называется интегрируемой на по Риману. Основные свойства определенного интеграла I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.  , где х, t – любые буквы.II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.  III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.  IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.  V. Постоянный множитель можно выносить за знак определенного интеграла.  VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.  43 Формула Ньютона — Лейбница Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определённого интеграла и вычислением первообразной.
44 Вычисление площадей с помощью интеграла. 1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b : 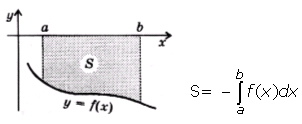 2.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и прямыми х=а, х= b : 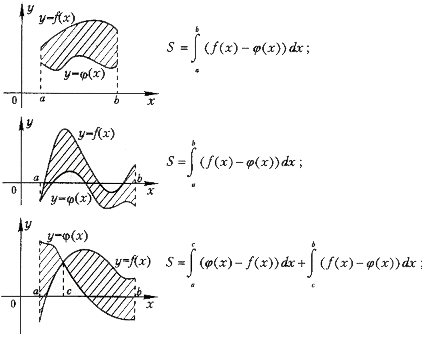 3.Площадь фигуры, ограниченной графиками непрерывных функций f (x) и : 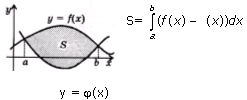 4.Площадь фигуры, ограниченной графиками непрерывных функций f (x), и осью Ох: 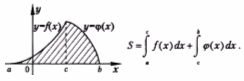 45 Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной При выводе формулы интегрирования по частям было получено равенство u dv = d (uv) – v du. Проинтегрировав его в пределах от a до b и учитывая теорему 4 параграфа о свойствах определённого интеграла, получим Как это следует из теоремы 2 параграфа о свойствах неопределённого интеграла, первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде получаем формулу интегрирования по частям для вычисления определенного интеграла: |
и 
на области определения;
, где k – произвольная константа.
