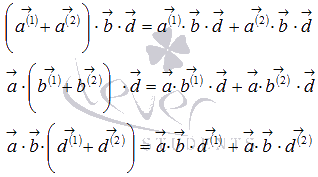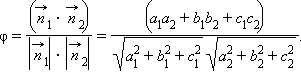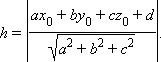Билеты по матану. Матрицей AAmn порядка mn называется прямоугольная таблица чисел, содержащая m строк и n столбцов

Название	Матрицей AAmn порядка mn называется прямоугольная таблица чисел, содержащая m строк и n столбцов
Анкор	Билеты по матану.docx
Дата	02.05.2017
Размер	1.28 Mb.
Формат файла
Имя файла	Билеты по матану.docx
Тип	Документы #6280
страница	2 из 6

1 2 3 4 5 6

Замечание. Если не указано положение полюса и полярной оси относительно декартовой системы координат, то считаем, что полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс.

9 Векторы. Сложение и вычитание векторов. Умножение вектора на число.

В
Вектор – это направленный отрезок, то есть такой отрезок, для которого указано, какая из его граничных точек является его началом, а какая – концом.

Конец ветора

Начало вектора

А

Вектор АВ

Длина ветора АВ – это длинна отрезка АВ ( |AB|)

Два ветора называются коллинеарными, если она лежат либо на одной прямой, либо на параллельных прямых. Если лежат в одном направление – сонаправленные, в разных – противоположно направленные. Два ветора равны если они сонаправленны и равны по длинне.

Сложение векторов (сумма векторов) a + b есть операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора cравен: с_i = a_i + b_i

Правило треугольника и правило параллелеограмма

с

в

а

с

Свойства сложения

а + 0 = а
а + в = в +а
(а +в) + с = а + (в + с)

Вычитание векторов (разность векторов) a - b есть операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен: сi = ai – bi

Умножение ветора на число

Произведение а ≠ 0 на К € R – это такой вектор в = Ка, который сонаправлен а при К › 0, и противоположно направлен а при К‹0, и длинна которого равна Ка. При К=0, в =0а=0.

10 Скалярное произведение векторов.

Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.

Скалярное произведение векторов и будем обозначать как

. Тогда формула для вычисления скалярного произведения имеет вид

, где и - длины векторов и соответственно, а

- угол между векторами и . Из определения скалярного произведения видно, что если хотя бы один из умножаемых векторов нулевой, то .

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов a и b.

То есть, для векторов на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид

а для векторов в трехмерном пространстве скалярное произведение в координатах находится как

Свойства.

свойство коммутативности скалярного произведения ;
свойство дистрибутивности или
сочетательное свойство или , где - произвольное действительное число;
скалярный квадрат вектора всегда не отрицателен , причем тогда и только тогда, когда вектор нулевой.

Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.

cos α =	a·b
	\|a\|·\|b\|

11 Векторное произведение векторов и его св-ва. Вычисление площадей

Векторным произведением двух векторов и , заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор , что

он является нулевым, если векторы и коллинеарны;
он перпендикулярен и вектору и вектору ();
его длина равна произведению длин векторов и на синус угла между ними ();
тройка векторов ориентирована так же, как и заданная система координат.

В прямоугольной системе координат трехмерного пространства векторное произведение есть определитель квадратной матрицы где первая строка которой есть орты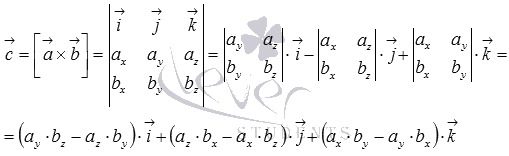

, во второй строке находятся координаты вектора , а в третьей – координаты вектора в заданной прямоугольной системе координат:
, формула

антикоммутативность ;
свойство дистрибутивности или ;
сочетательное свойство или , где - произвольное действительное число.

Площадь параллелограмма образованного векторами a и b равна модулю векторного произведения этих векторов: S = |a × b|

Площадь треугольника образованного векторами a и b равна половине модуля векторного произведения этих векторов:

S =	1	\|a × b\|
	2

12 Смешанное произв. Вектр.и его св-ва

Смешанным произведением трех векторов

и называется действительное число, равное скалярному произведению векторов

и , где

- векторное произведение векторов и .

Векторное произведение в координатах имеет вид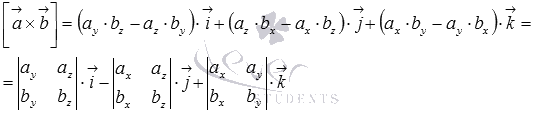
формула

а скалярное произведение векторов в прямоугольной системе координат равно

сумме произведений соответствующих координат, поэтому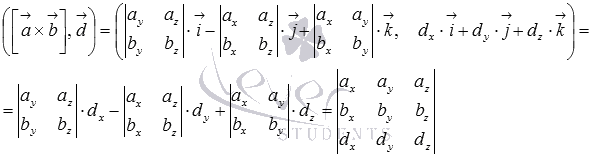
формула

свойства смешанного произведения:

;
;

Объем параллелепипеда, построенного на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен:

13 Условия колинеарности,компл и ортогонал.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.

Два ненулевых вектора и коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.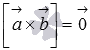
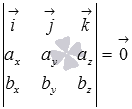формула

или

Для коллинеарности необходимо чтобы их координаты были связаны соотношениями: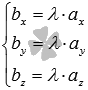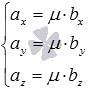

или

.или

Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.

Для компланарности трех векторов и трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.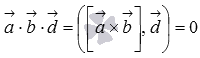

формула

Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам ( радиан).

Для перпендикулярности двух ненулевых векторов и необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство 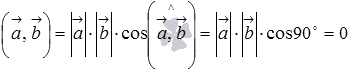формула

необходимое и достаточное условие перпендикулярности двух векторов в координатах имеет вид

на плоскости, а в трехмерном пространстве

.

14 прямая линия на плоскости и ее уравнения

Прямая (прямая линия) - это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида

A x + B y + C = 0

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

y = k x + b

где k - угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках

x	+	y	= 1
a		b

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки A(x₁, y₁) и B(x₂, y₂), такие что x₁ ≠ x₂ и y₁ ≠ y₂ то уравнение прямойможно найти, используя следующую формулу

x- x₁	=	y- y₁
x₂ - x₁	=	y₂ - y₁

Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

	x = l t+ x₀
	Y = m t+ y₀

где (x₀, y₀) - координаты точки лежащей на прямой, {l, m}- координаты направляющего вектора прямой.

Каноническое уравнение прямой на плоскости

Если известны координаты точки A(x₀, y₀) лежащей на прямой и направляющего вектора n= {l; m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x- x₀	=	y - y₀
l	=	m

15 Уравнение плоскости в Пространстве
Общее уравнение плоскости в декартовой системе координат записывается следующим образом:

ax + by + cz + d = 0.

Если известно, что плоскость проходит через точку с координатами (x₀, y₀, z₀), то ее уравнение можно привести к виду

a (x – x₀) + b (y – y₀) + c (z – z₀) = 0.

Уравнение

называется уравнением плоскости в отрезках на осях.

Нормаль к плоскости имеет координаты

Угол между двумя плоскостями легко вычисляется по формуле скалярного произведения. Если эти плоскости задаются уравнениями a₁x + b₁y + c₁z + d₁ = 0 и a₂x + b₂y + c₂z + d₂ = 0, то угол между плоскостями равняется

http://www.mathematics.ru/courses/stereometry/content/javagifs/63229915696984-3.gif

Расстояние от точки (x₀; y₀; z₀) до плоскости, задаваемой уравнением ax + by + cz + d = 0, равно

16 Уравнение прямой в пространстве

Векторное параметрическое уравнение прямой в пространстве:

$\vec r=\vec{r}_0+t\vec a,\quad t\in(-\infty,\;+\infty),$

где — радиус-вектор некоторой фиксированной точки лежащей на прямой, — ненулевой вектор, коллинеарный этой прямой (называемый её направляющим вектором), — радиус-вектор произвольной точки прямой.

Параметрические уравнения прямой в пространстве:

$x=x_0+t\alpha,\;y=y_0+t\beta,\;z=z_0+t\gamma,\quad t\in(-\infty,\;+\infty),$

где $(x_0,\;y_0,\;z_0)$ — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.

Каноническое уравнение прямой в пространстве:

$\frac{x-x_0}{\alpha}=\frac{y-y_0}{\beta}=\frac{z-z_0}{\gamma},$

где $(x_0,\;y_0,\;z_0)$ — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.

Общее векторное уравнение прямой^[в пространстве:

Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:

$(\vec r,\;\vec n_1)+d_1=0$ и $(\vec r,\;\vec n_2)+d_2=0,$

то уравнение прямой можно задать системой этих уравнений: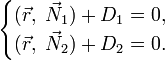

$\begin{cases}(\vec r,\;\vec n_1)+d_1=0,\\ (\vec r,\;\vec n_2)+d_2=0.\end{cases}$

Векторное уравнение прямой в пространстве

Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой на фиксированный направляющий вектор прямой :

$[\vec r, \vec a]=\vec m,$

где фиксированный вектор , ортогональный вектору , можно найти, подставляя в это уравнение радиус-вектор какой-нибудь одной известной точки прямой.

1 2 3 4 5 6