Билеты по матану. Матрицей AAmn порядка mn называется прямоугольная таблица чисел, содержащая m строк и n столбцов

Название	Матрицей AAmn порядка mn называется прямоугольная таблица чисел, содержащая m строк и n столбцов
Анкор	Билеты по матану.docx
Дата	02.05.2017
Размер	1.28 Mb.
Формат файла
Имя файла	Билеты по матану.docx
Тип	Документы #6280
страница	4 из 6

1 2 3 4 5 6

Точки разрыва первого и второго рода

если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода. Точки устранимого разрыва являются точками разрыва первого рода;

если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

25 Непрерывность элементарных функций

Все элементарные функции являются непрерывными в любой точке свой области определения.

Функция называется элементарной, если она построена из конечного числа композиций и комбинаций
(с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функций. Множество основных элементарных функций включает в себя:

Алгебраические многочлены ;

Рациональные дроби ;

Степенные функции ;

Показательные функции ;

Логарифмические функции ;

Тригонометрические функции ;

Обратные тригонометрические функции ;

Гиперболические функции ;

Обратные гиперболические функции .

26 Асимптоты к графикам

Функции и их способы нахождения

Прямая  называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений  или  равно  или  .

Прямая  называется горизонтальной асимптотой графика функции , если хотя бы одно из предельных значений  или  равно  .

Прямая  называется наклонной асимптотой графика функции , если

Порядок нахождения асимптот

1.) Нахождение вертикальных асимптот.
2.) Нахождение двух пределов $latex: \lim_{x \to \pm \infty}\frac{f(x)}{x}=k$
3.) Нахождение двух пределов $latex: \lim_{x \to \pm \infty}(f(x)-kx)=b$ :

если  в п. 2.), то , и предел $latex: \lim_{x \to \pm \infty}(f(x)-kx)=b$ ищется по формуле горизонтальной асимптоты, $latex: \lim_{x \to \pm \infty}f(x)=a$ .

Наклонная асимптота — выделение целой части

Также наклонную асимптоту можно найти, выделив целую часть. Например:

Дана функция $</h2>f(x)=\frac{2x^3+5x^2+1}{x^2+1}$ .

Разделив нацело числитель на знаменатель, получим:

$</h2>f(x)=2x+5+ \frac{-2x-4}{x^2+1}=2x+5+(-2) \cdot \frac{x+2}{x^2+1}$ .

При   ,    $\frac{x+2}{x^2+1} \to 0$ ,   то есть:

$\lim_{x \to \pm \infty}f(x)=\lim_{x \to \pm \infty}(2x+5)= \pm \infty$ ,

и  является искомым уравнением асимптоты.

27 Производная функции в точке.Ур.касател.,непрер.
Производной функции в точке  называется предел отношения приращения функции  к соответствующему приращению аргумента , при условие, что .()

Геометрический смысл производной:

Производная в точке  равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна .
Иными словами Производная функции  в точке  равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.

Уравнение касательной и нормали к линии в точке

Уравнение касательной: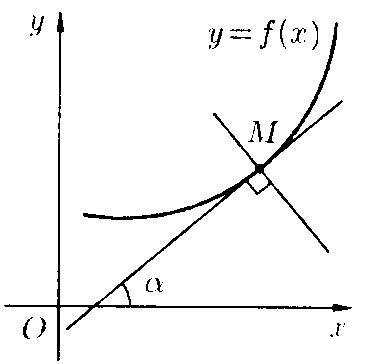

.

Уравнение нормали:

Непрерывность функции, имеющей производную..

Если функция y = f(x) дифференцируема в некоторой точке x = x0, то она в этой точке непрерывна.

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x0 функция y = f(x) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x| непрерывна для всех x (–< х < ), но в точке x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.
28Физический смысл первой производной

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

Физический смысл производной функции

Если положение точки при её движении по числовой прямой задаётся функцией S = f(t), где t – время движения, то производная функции S – мгновенная скорость движения в момент времени t. По аналогии с этой моделью вообще говорят о том, что производная функции у = f(x) – скорость изменения функции в точке х.

Непрерывность функции, имеющей производную. Теорема.

Если функция y = f(x) дифференцируема в некоторой точке x = x0, то она в этой точке непрерывна.

29 правила нахождения производная суммы разности произведения отношения функций

Производная суммы и разности

(f + g)’ = f ’ + g ’

(f − g)’ = f ’ − g ’

Производная произведения

(f · g) ’ = f ’ · g + f · g ’

Производная частного

30 Таблица производных основных элементарных функций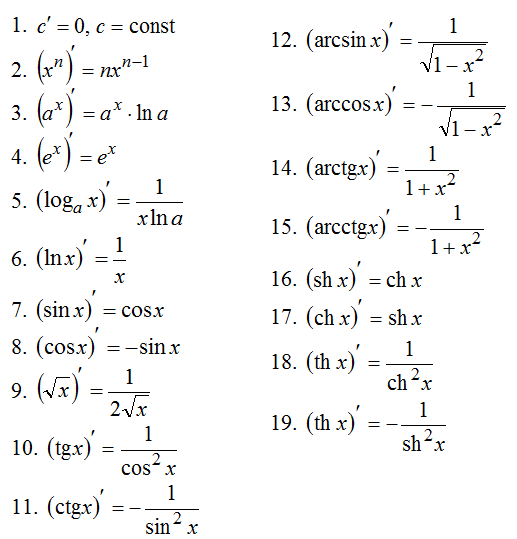

31 Производ. Слож. Функц

Производная сложной функции. Производная функции, заданной параметрически

Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или



Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле



Производная функции заданной параметрически.

.

.

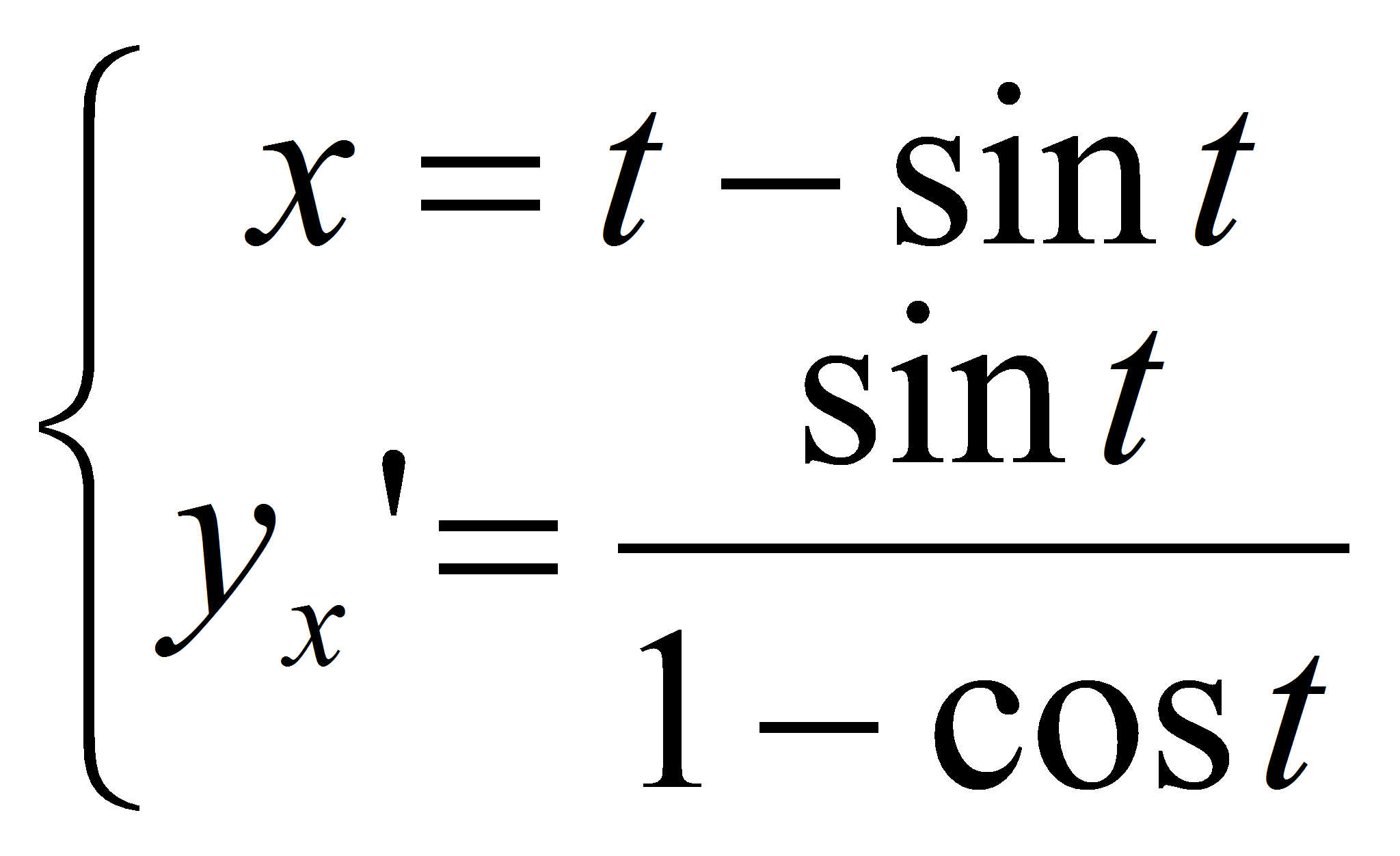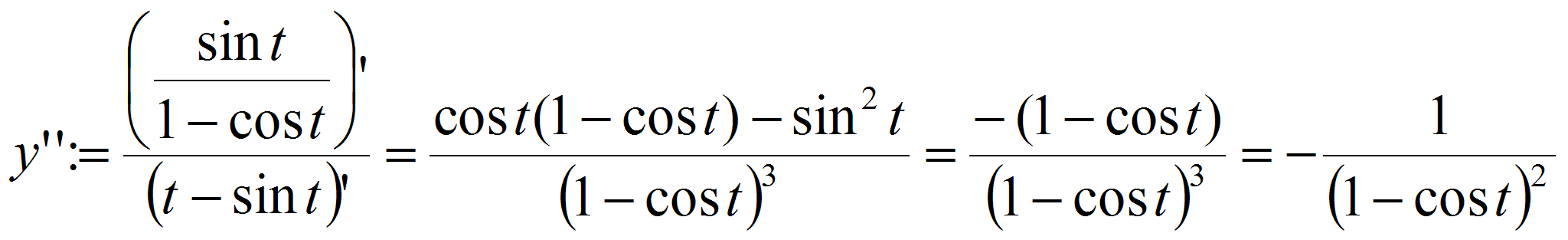32 Произв и диффер. Высш.порядк

Пусть теперь производная -го порядка  определена в некоторой окрестности точки  и дифференцируема. Тогда

$f^{(n+1)}(x_0) = \left(f^{(n)}\right)\'(x_0).$

Если функция  имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от   может иметь в некоторой точке  частные производные по той же или по любой другой переменной. Для исходной функции  эти производные будут частными производными второго порядка (или вторыми частными производными).

$</h2>u\'\'_{x^2} = f\'\'_{x^2}(x_0, y_0, z_0)$ или $</h2>\frac{\partial^2 u}{\partial x^2} = \frac{\partial^2 f(x_0, y_0, z_0)}{\partial x^2}$

$</h2>u\'\'_{xy} = f\'\'_{xy}(x_0, y_0, z_0)$ или $</h2>\frac{\partial^2 u}{\partial x \partial y} = \frac{\partial^2 f(x_0, y_0, z_0)}{\partial x \partial y}$

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

$</h2>u\'\'_{xy} = f\'\'_{xy}(x_0, y_0, z_0)$

Дифференциалом порядка n, где n > 1, от функции   в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1), то есть

$</h2>d^nz= d(d^{n-1}z)$ .

Для функции, зависящей от одной переменной   второй и третий дифференциалы выглядят так:

$</h2>d^2z = d(dz) = d(z\'dx) = dz\'dx = (z\'\'dx)dx = z\'\'dx^2$

$</h2>d^3z = d(d^2z) = d(z\'\'dx^2) = dz\'\'dx^2 = (z\'\'\'dx)dx^2 = z\'\'\'dx^3$

Отсюда можно вывести общий вид дифференциала n-го порядка от функции  :

$</h2>d^nz = z^{(n)}dx^n$

33 Монотон.диффер.высш.функц.

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

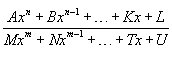Пусть дана функция  Тогда

функция  называется возраста́ющей на , если

$\forall x,y\in m,\; x> y \Rightarrow f(x) \ge f(y)$ .

функция  называется стро́го возраста́ющей на , если

$\forall x,y\in m,\; x> y \Rightarrow f(x) > f(y)$ .

функция  называется убыва́ющей на , если

$\forall x,y\in m,\; x> y \Rightarrow f(x) \le f(y)$ .

функция  называется стро́го убыва́ющей на , если

$\forall x,y\in m,\; x> y \Rightarrow f(x) < f(y)$ .
1 2 3 4 5 6