Часть 2_4 Формулы Библ. 9. Основные понятия и формулы I. Векторная алгебра
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
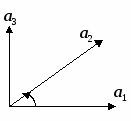
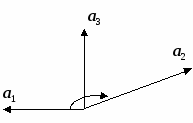
9. Основные понятия и формулыI. Векторная алгебра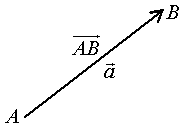 Вектор - направленный отрезок. Векторы называются коллинеарными, если лежат на одной прямой либо на параллельных прямых. Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Два вектора равны, если они коллинеарны, имеют одинаковую длину и направление. Линейные операции над векторами 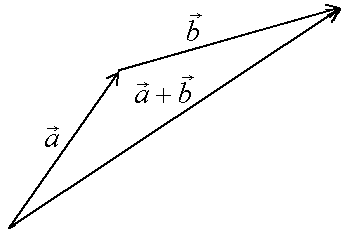 Суммой Свойства: 1 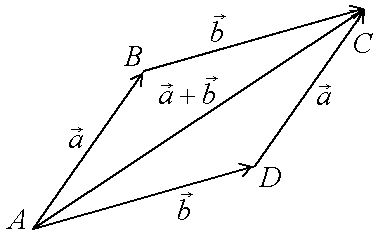 ˚. 2˚. 3˚. 4 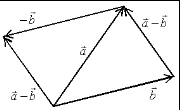 ˚. Для каждого вектора ˚. Для каждого вектора Разностью векторов идущий из конца вектора Произведение в 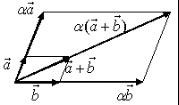 ещественное число ещественное число 5˚. 6˚. 7˚. 8˚. Базис и координаты Базисом в пространстве называются три некомпланарных вектора, взятые в определенном порядке. Базисом на плоскости будем называть два неколлинеарных вектора на этой плоскости, взятые в определенном порядке. Базисом на прямой будем называть любой ненулевой вектор этой прямой. 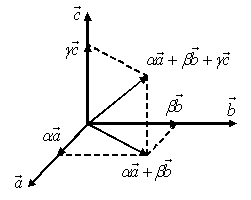 Каждый вектор может быть разложен по базису в пространстве и это разложение единственно. Каждый вектор может быть разложен по базису в пространстве и это разложение единственно.Коэффициенты разложения вектора по базису называются координатами вектора в данном базисе и в каждом базисе определяются однозначно: При сложении двух векторов Системой координат в пространстве называют совокупность базиса Вектор Координатами точки Таким образом, координаты радиус-вектора Ортонормированный базис. Декартова прямоугольная система координат Пусть в качестве базиса выбраны три взаимно перпендикулярных вектора с длинами, равными единице. Обозначения: Т 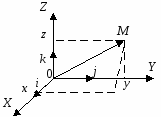 акой базис называется ортонормированным (ОНБ). Векторы Координаты любого вектора в этом базисе называются декартовыми координатами вектора: Прямые линии, проведенные через начало координат по направлениям базисных векторов, называются координатными осями: Декартовы прямоугольные координаты Здесь Вектор 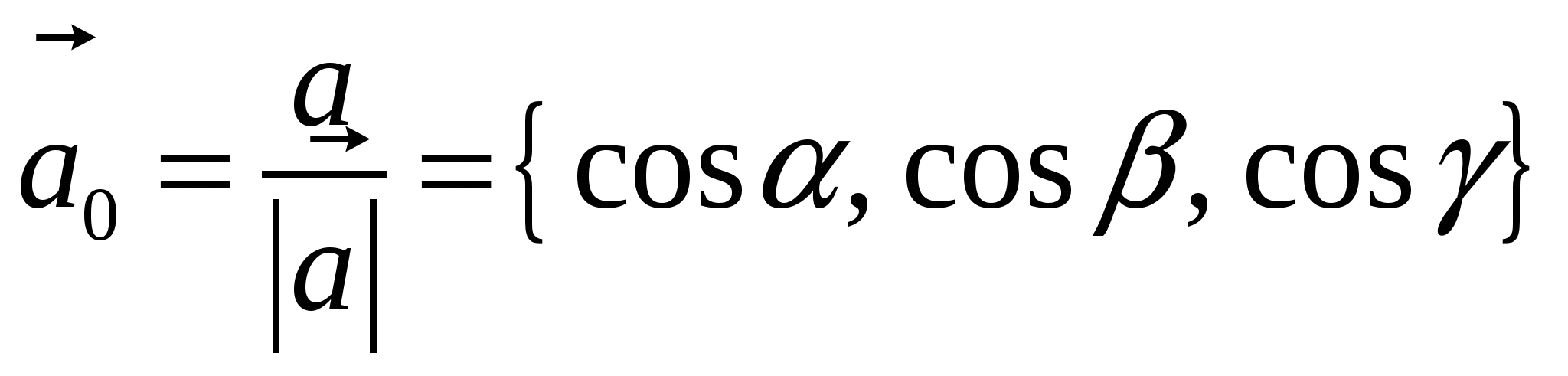 представляет собой вектор единичной длины данного направления, или орт данного направления. Для направляющих косинусов справедливо соотношение: представляет собой вектор единичной длины данного направления, или орт данного направления. Для направляющих косинусов справедливо соотношение:П 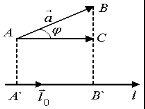 роекция вектора роекция вектора Если 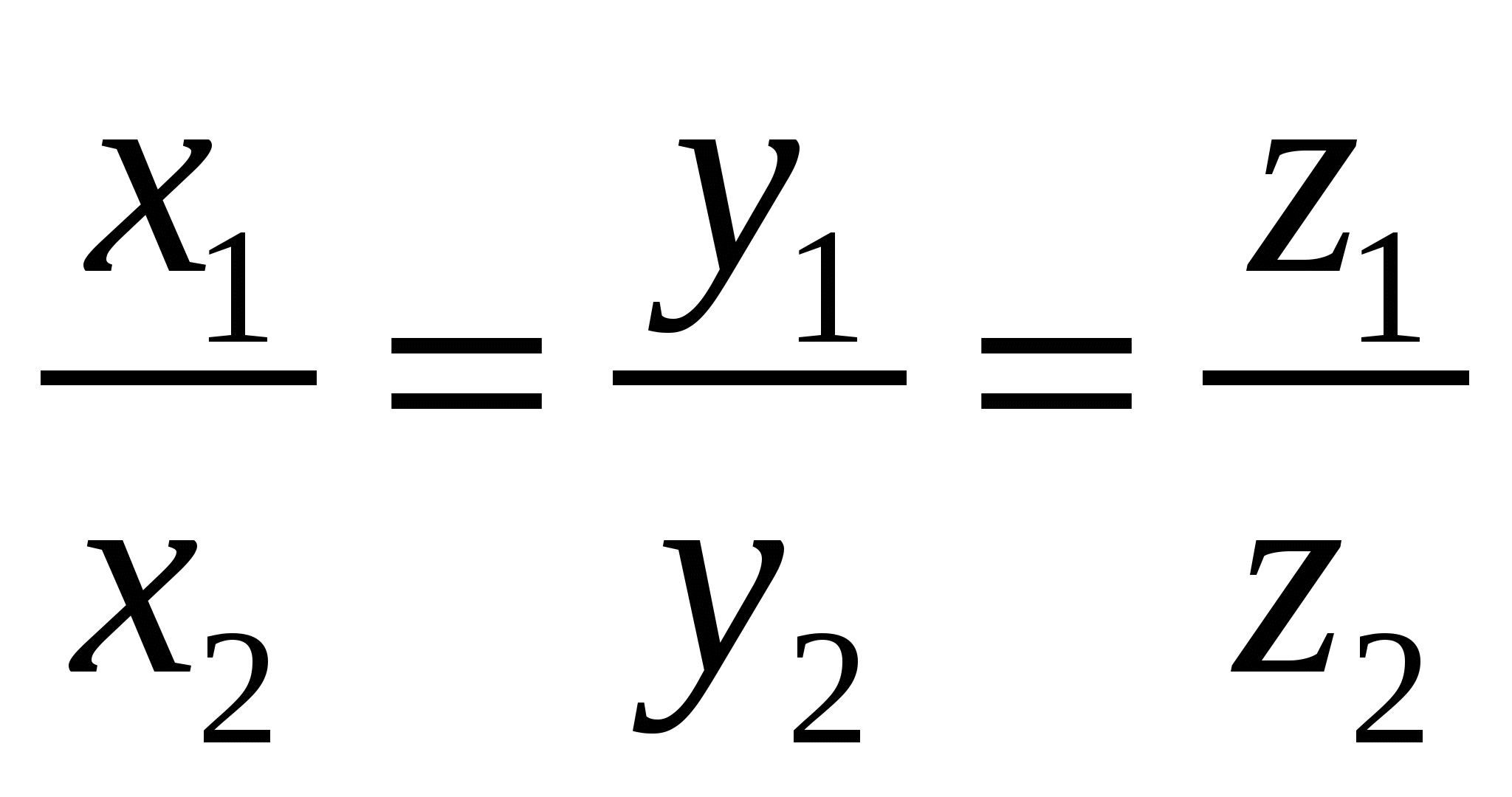 . .Скалярное произведение векторов Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними: Если Алгебраические и геометрические свойства скалярного произведения: 1°. 2°. 3°. 4°. 5°. 6°. 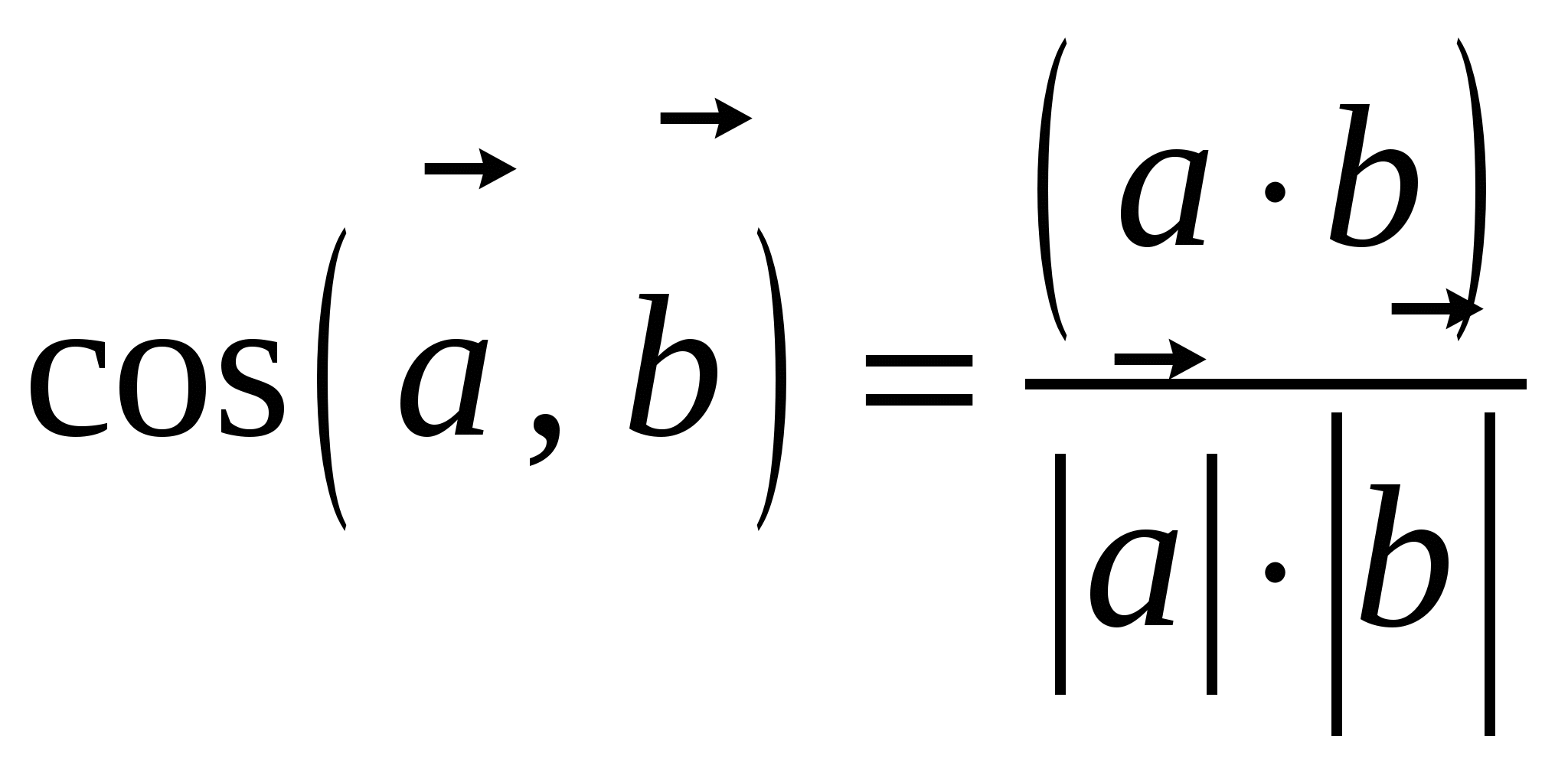 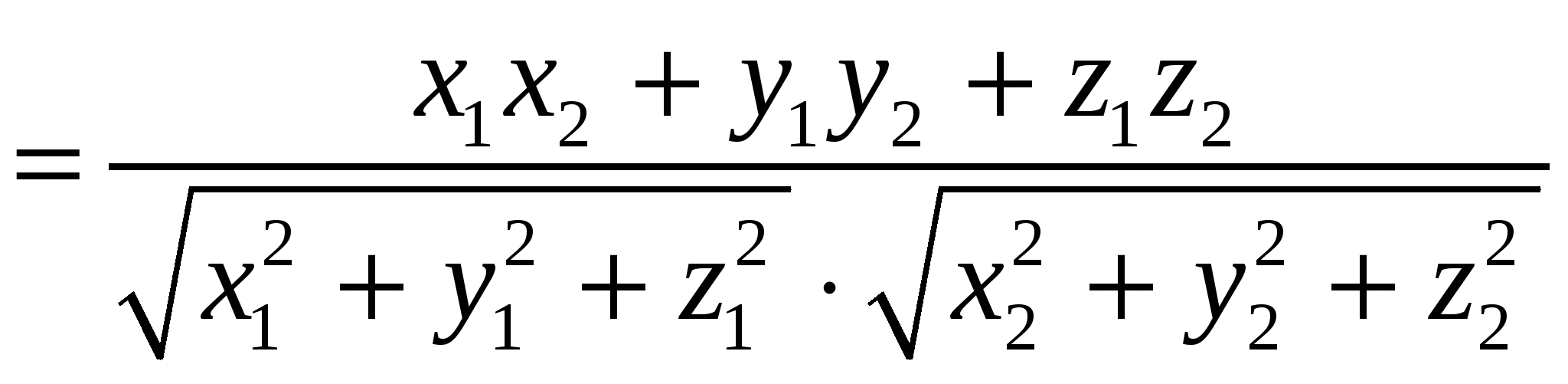 . .7°. 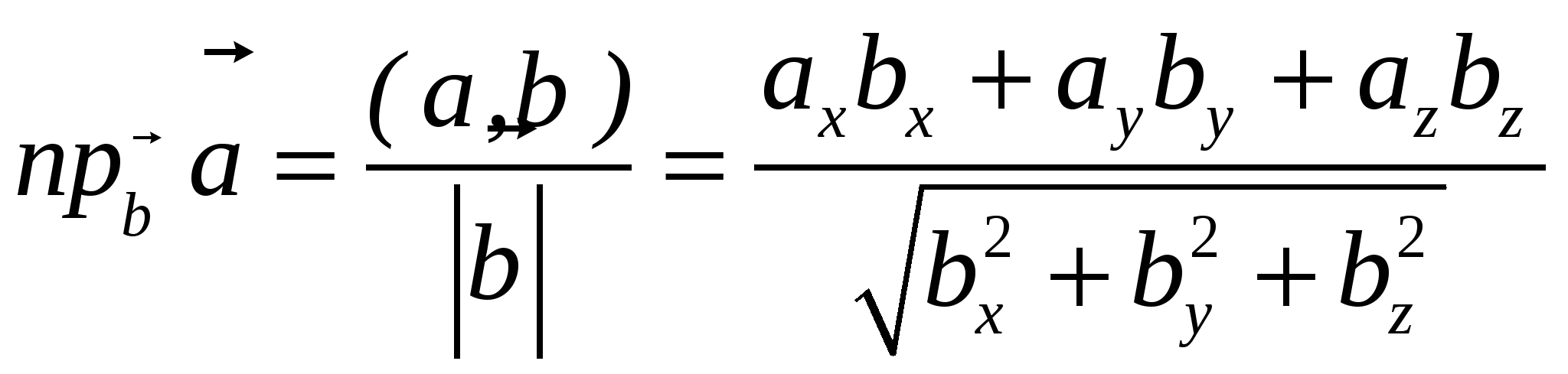 , , 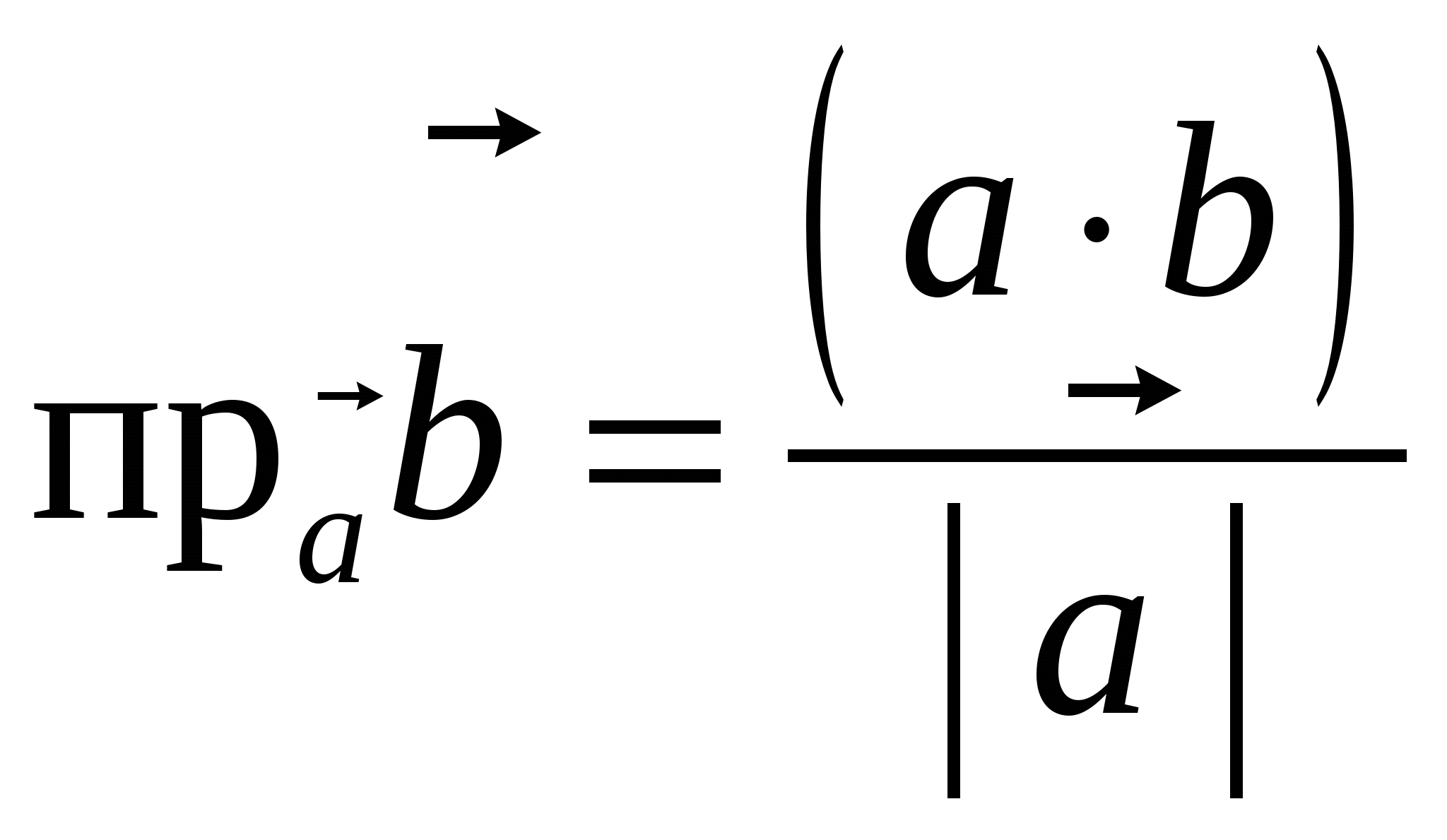 . .8°. для ненулевых 9°. 10°. 11°. Направляющие косинусы вектора: 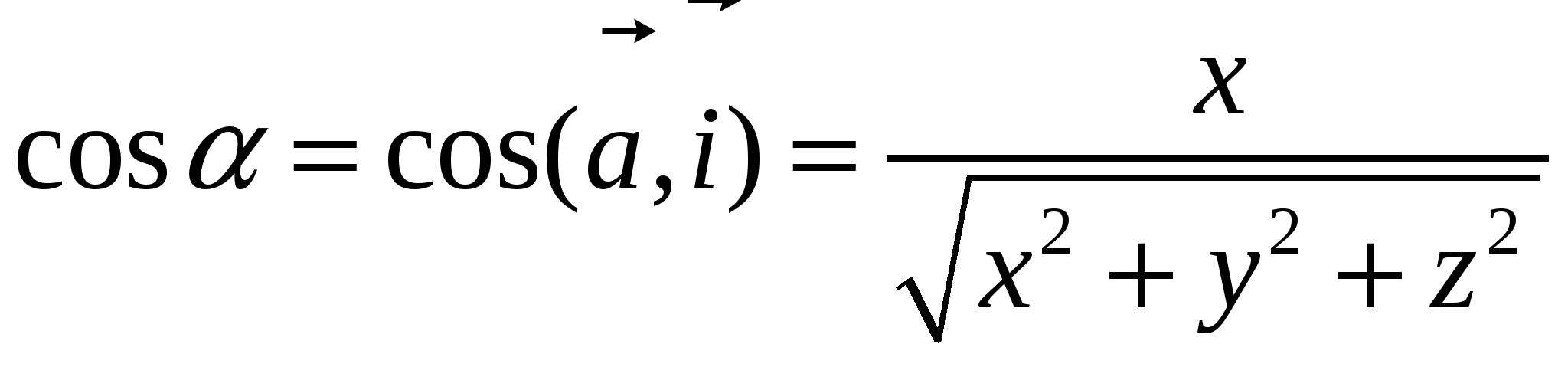 , , 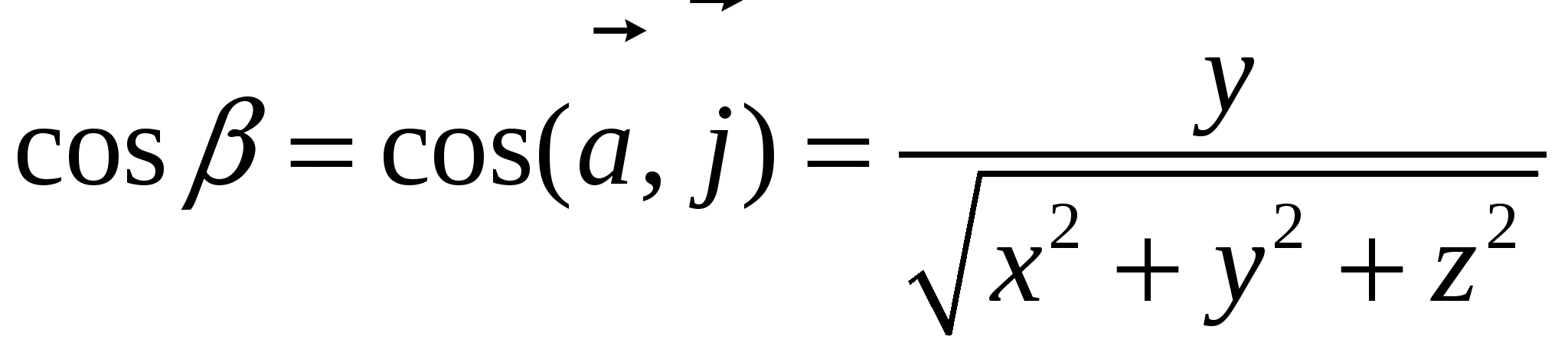 , , 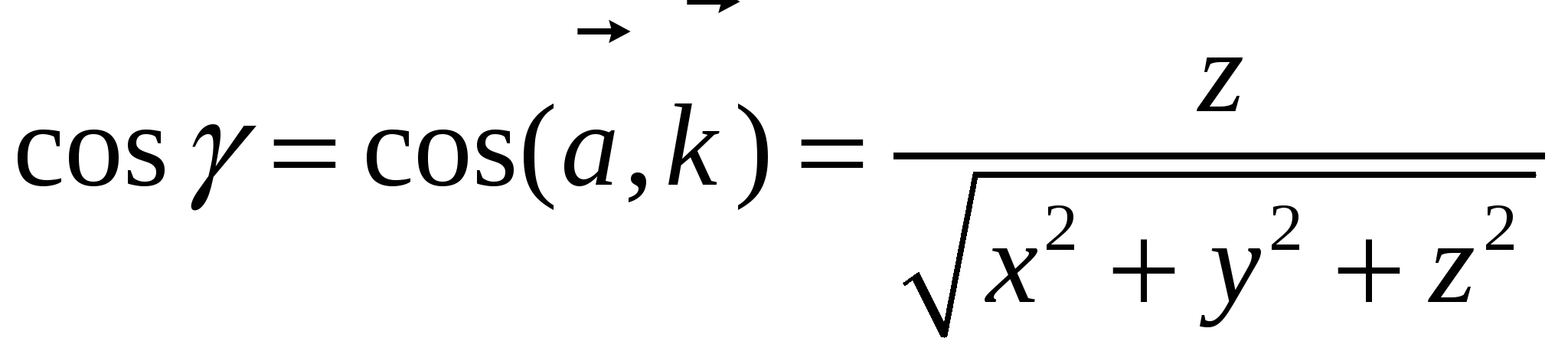 ; ; cos2 α + cos2 β + cos2 Упорядоченная тройка некомпланарных векторов
При перестановке местами двух соседних векторов ориентация тройки меняется. Если тройки { При круговой (циклической) перестановке векторов ориентация тройки не меняется. Векторное произведение векторов Векторным произведением вектора 1). Длина вектора 2). Вектор перпендикулярен плоскости, в которой лежат векторы 3). Вектор Алгебраические и геометрические свойства векторного произведения: 1°. 2. 3. 4 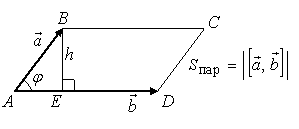 . . 5. Площадь параллелограмма, построенного на векторах 6. нулевым вектором. Выражение векторного произведения через декартовы координаты сомножителей Если 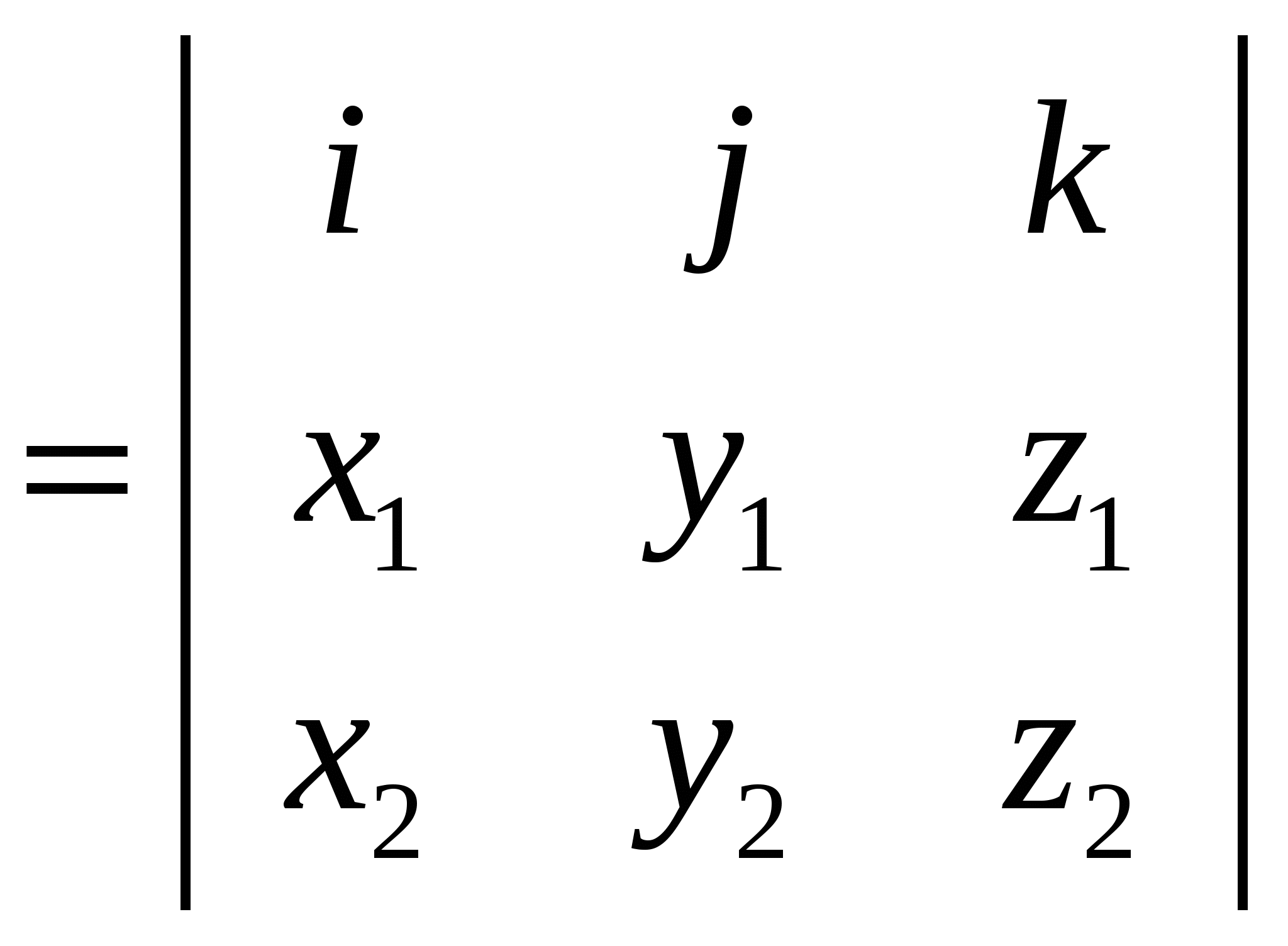 . .Смешанное произведение векторов Смешанное произведение некомпланарных векторов по абсолютной величине равно объему параллелепипеда, построенного на этих векторах, приведенных к одному началу, Е 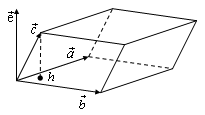 сли же векторы сли же векторы 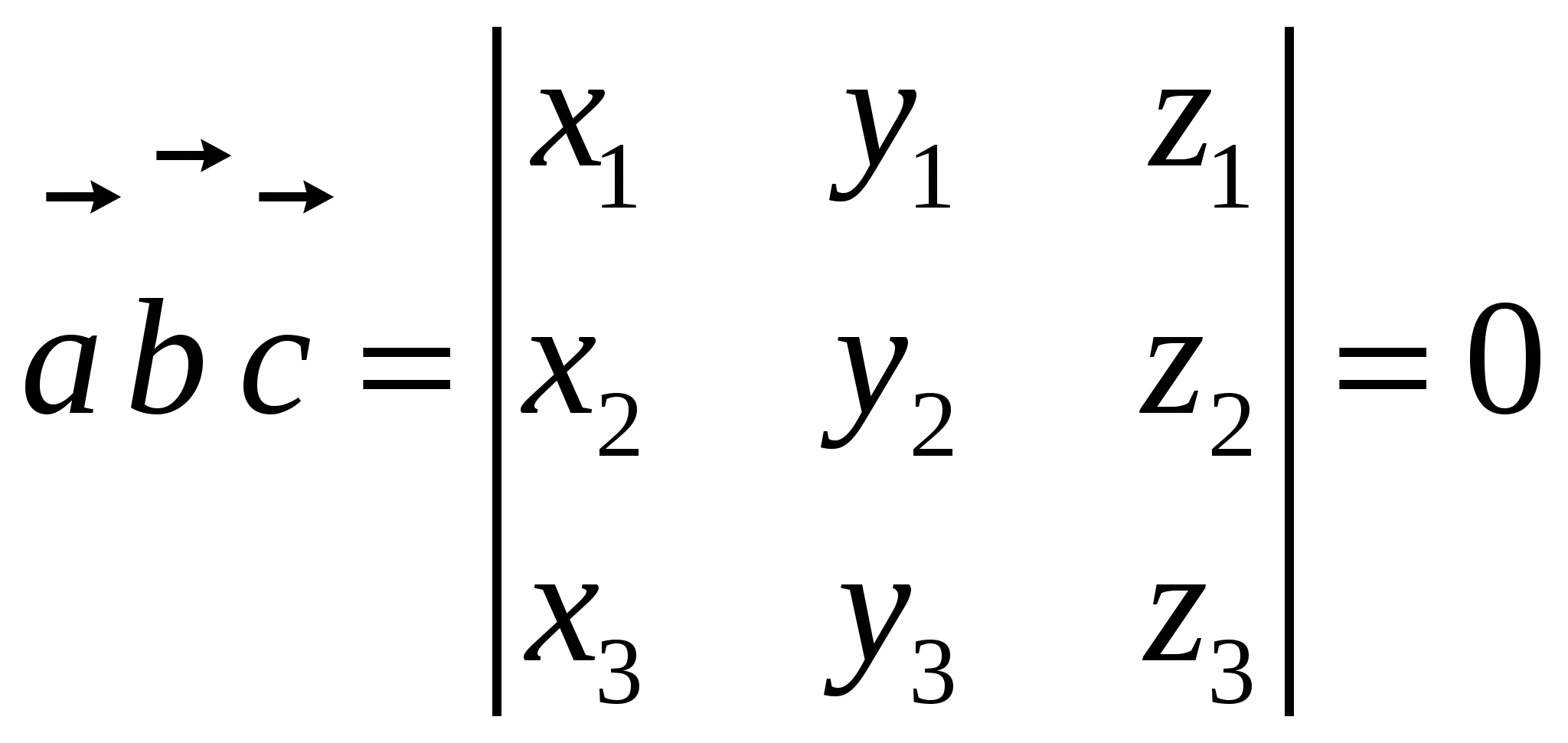 . .Смешанное произведение зависит от порядка сомножителей, но не зависит от того, какие сомножители связаны первичным знаком векторного произведения. Если 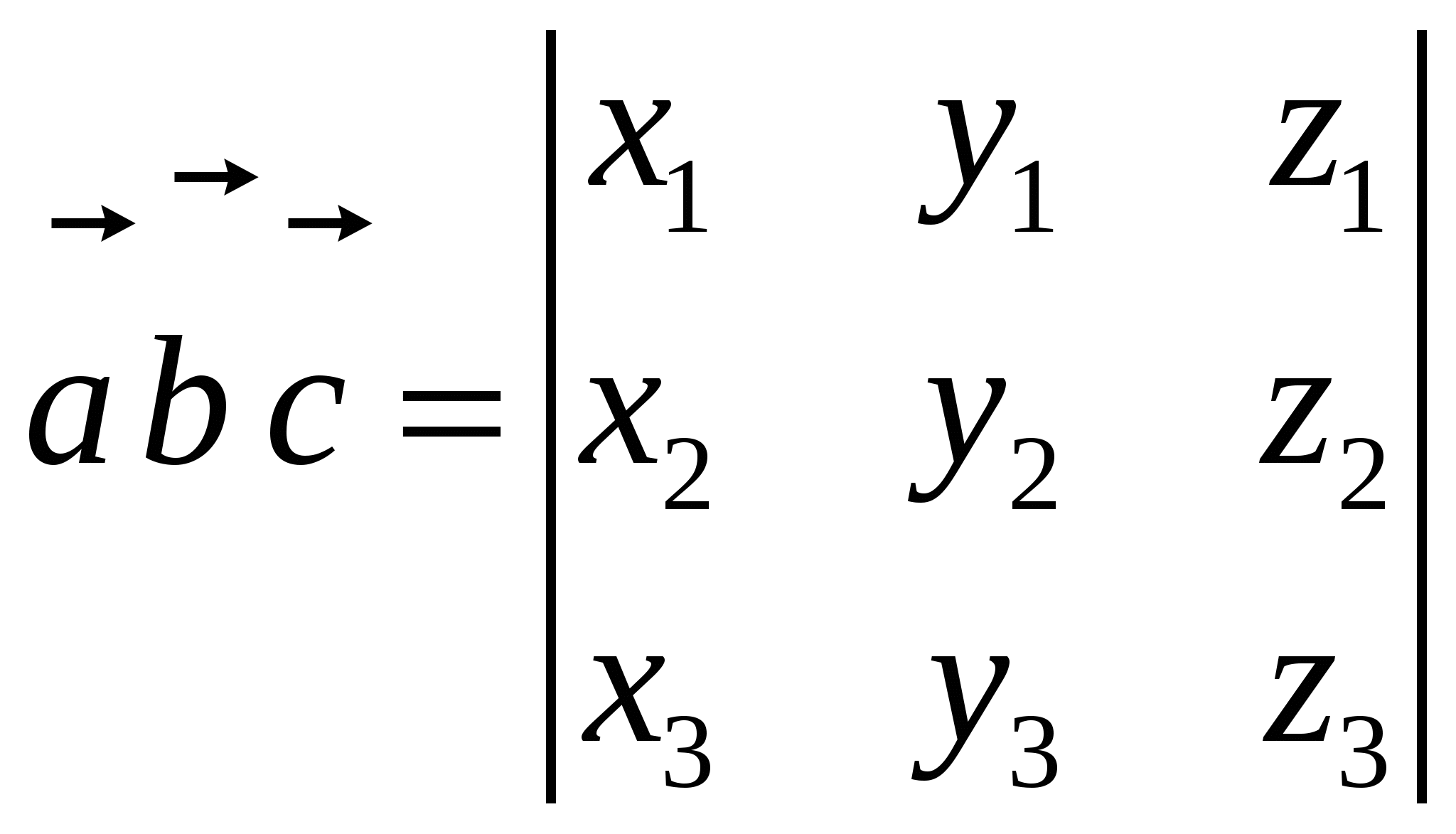 . . |