Часть 2_4 Формулы Библ. 9. Основные понятия и формулы I. Векторная алгебра
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
Линии в полярной системе координатПолярные координаты Связь полярных координат с декартовымиДля M(x,y) и M( 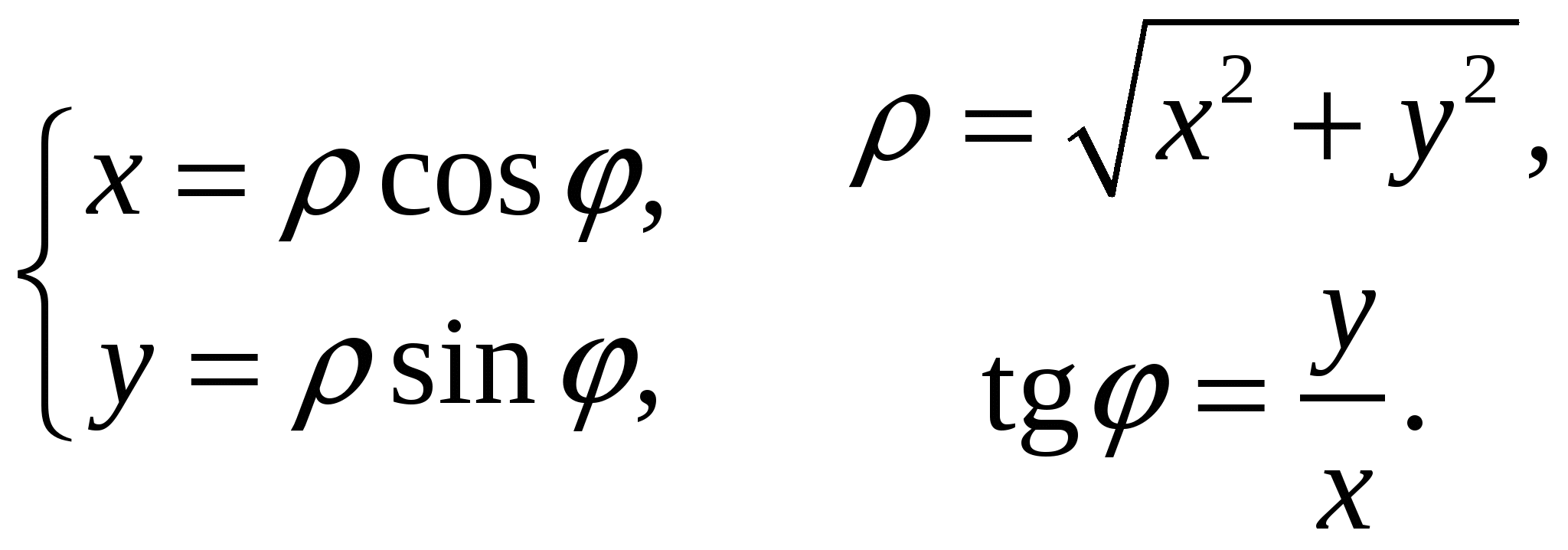 О | ||||||||||||||||||||||||||||||||||||
Эллипсоид | 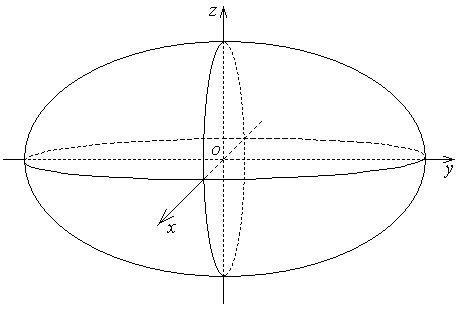 | |
| Гиперболоиды | ||
| Однополостный гиперболоид | 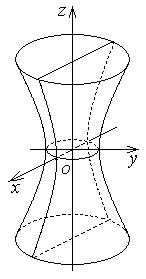 | |
| Двуполостный гиперболоид | 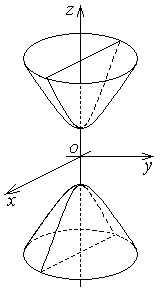 | |
| Параболоиды | ||
| Эллиптический параболоид | 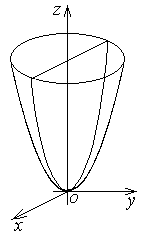 | |
| Гиперболический параболоид | 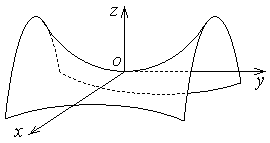 | |
| Конус второго порядка | 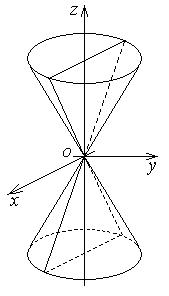 | |
| Цилиндры | ||
Эллиптический цилиндр | 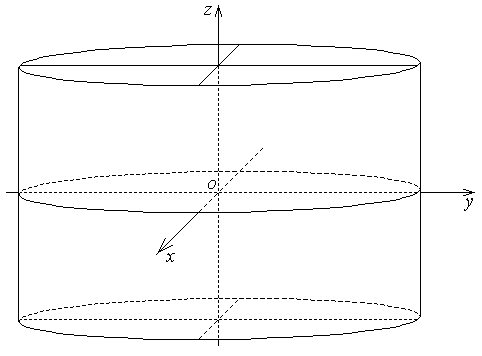 | |
Гиперболический цилиндр | 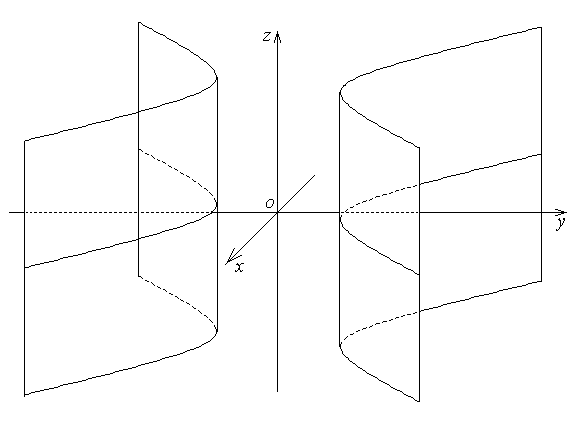 | |
Параболический цилиндр | 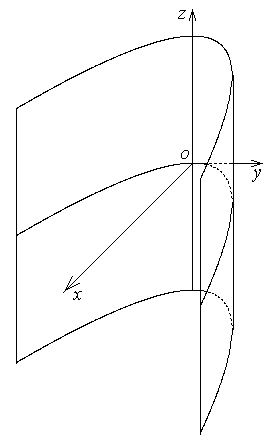 | |
10. БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Ильин В.А. Аналитическая геометрия / В.А. Ильин, Э.Г. Позняк.
М.: Наука, ГФМЛ, 1988.
Бугров Е.С. Элементы линейной алгебры и аналитической геометрии /
Е.С. Бугров, С.М. Никольский. М.: Наука, 1984.
Бугров Е.С. Высшая математика: Задачник / Е.С. Бугров, С.М. Никольский. М.: Наука, 1982.
Сборник задач по математике для втузов: В 4 ч. Ч. 1: Векторная алгебра и аналитическая геометрия. Определители и матрицы системы линейных уравнений. Линейная алгебра. Основы общей алгебры / А. В. Ефимов,
А. Ф. Каракулин, И. Б. Кожухов [и др.]; под ред. А. В. Ефимова,
А. С. Поспелова. 4-е изд., перераб. и доп. М.: Физматлит, 2003. - 288 с.: ил.; 21 см. - ISBN 5-940520-34-0.
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры /
Д.В. Беклемишев. М.: Наука, 1984.
Наумов В.А. Руководство к решению задач по линейной алгебре и аналитической геометрии / В.А.Наумов. М.: Наука, 1993.
Фадеев Д.К. Сборник задач по высшей алгебре / Д.К. Фадеев,
Н.С. Соминский. М.: Наука, 1997.
Беклемишева Л.А. Сборник задач по аналитической геометрии и линейной алгебре / Л.А. Беклемишева, А.Ю. Петрович, И.А. Чубаров. М.: Наука, 1987.
Кузнецов Л.А. Сборник заданий по высшей математике / Л.А. Кузнецов. М.: Высшая школа, 1994.
Минорский В.П. Сборник задач по высшей математике / В.П. Минорский. М.: Физматгиз, 1961.
Клетенник Д.В. Сборник задач по аналитической геометрии /
Д.В. Клетенник. М.: Наука, 1986.
Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии /
О.Н. Цубербиллер. М.: Наука, 1970.
Косторкин А.И. Линейная алгебраическая геометрия / А.И. Косторкин,
Ю.И. Манин. М.: Наука, 1986.
Бахвалов С.Б. Сборник задач по аналитической геометрии /
С.Б. Бахвалов, П.С. Моденов, А.С. Пархоменко. М.: Наука, 1964.

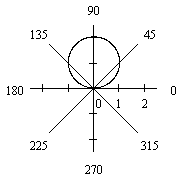 кружности
кружности 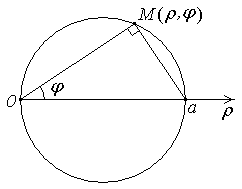
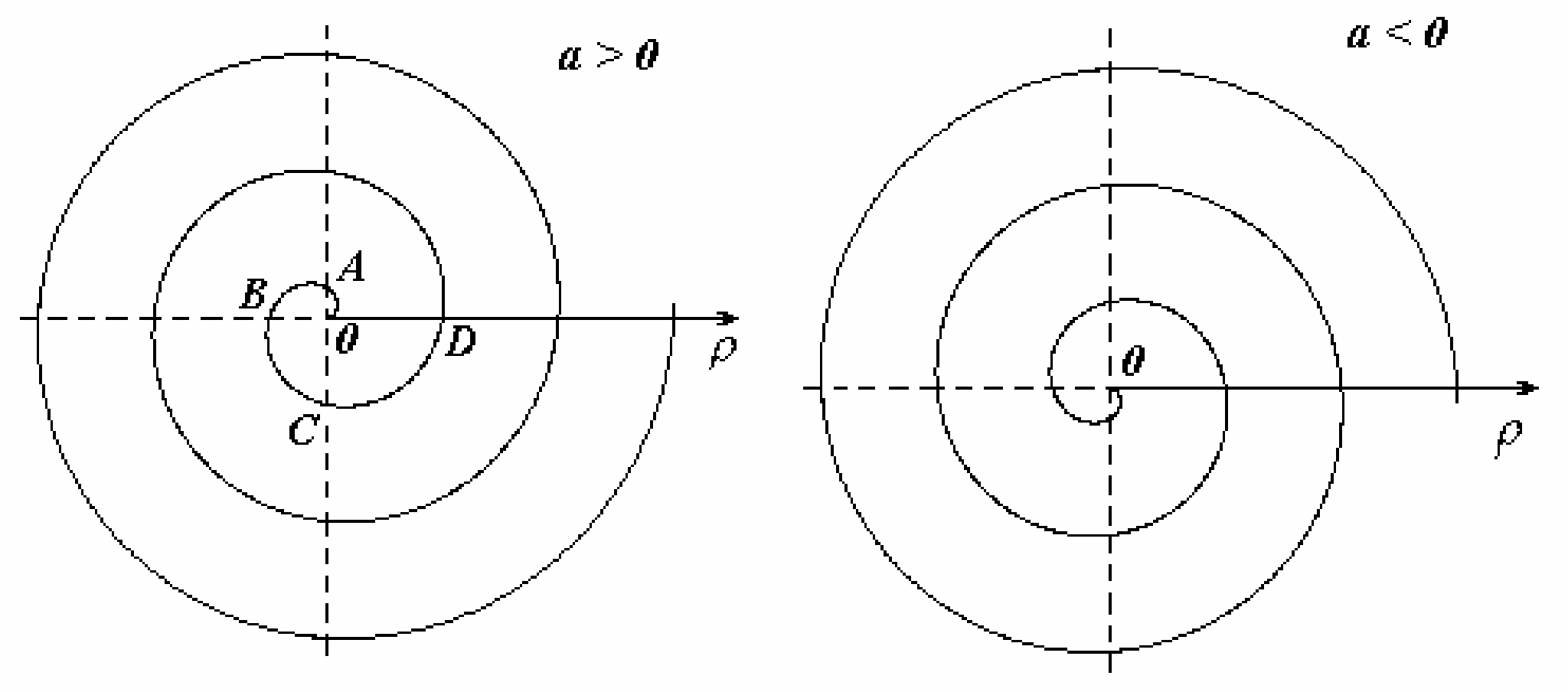
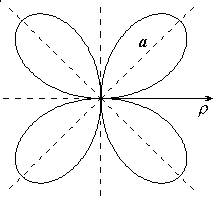
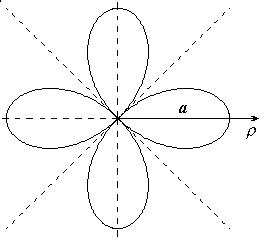
 , a > 0.
, a > 0.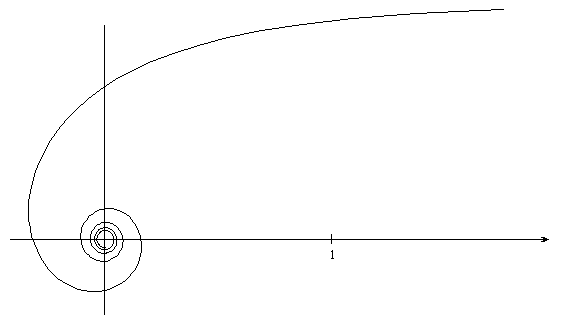
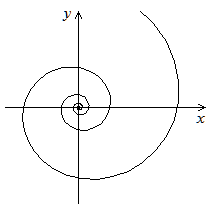
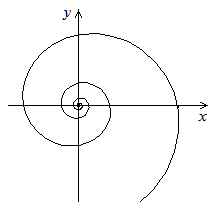
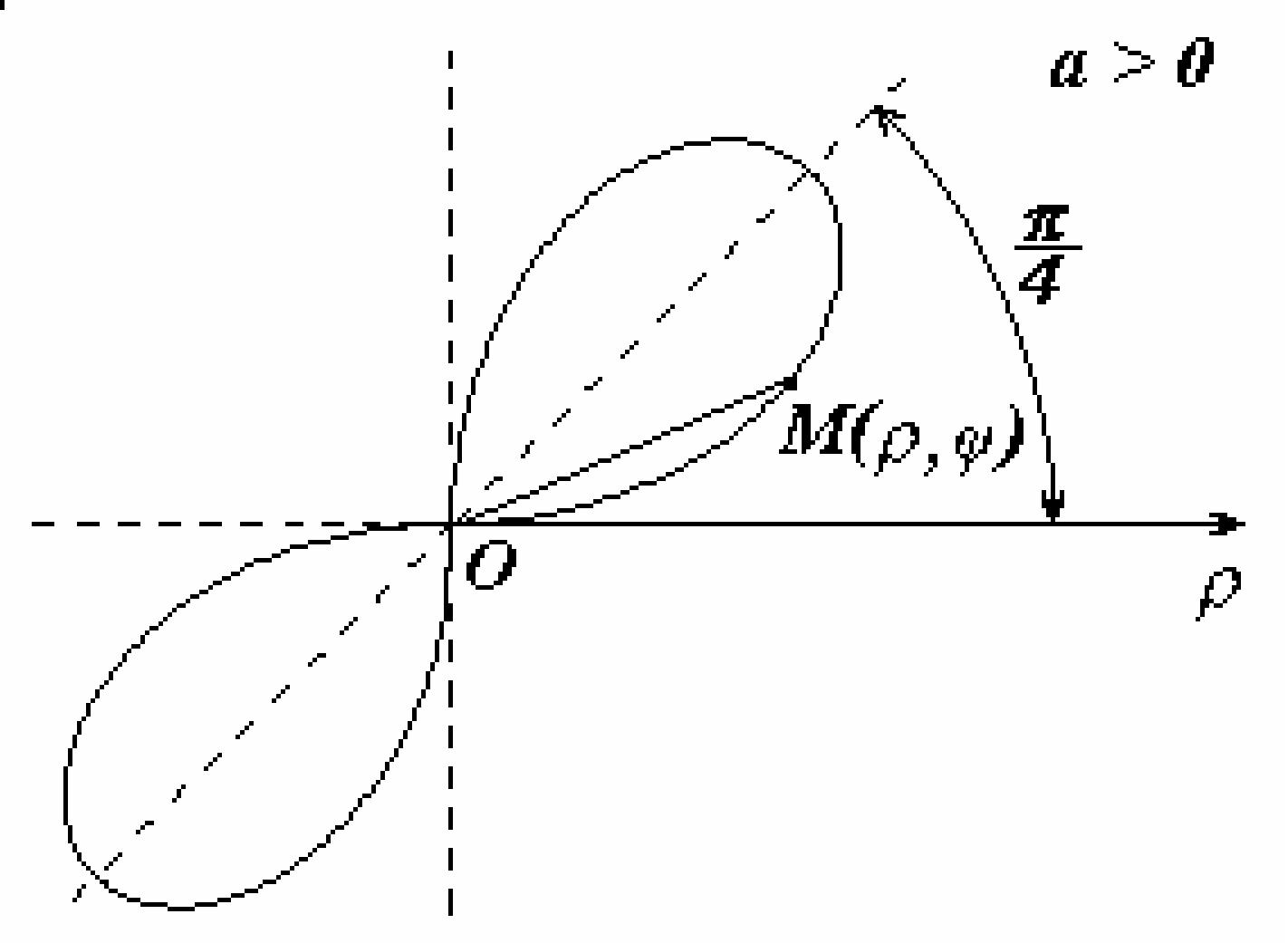
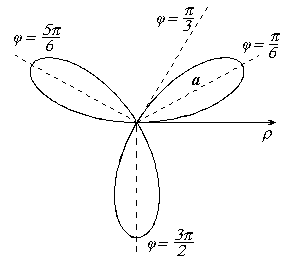
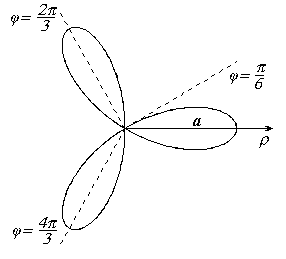
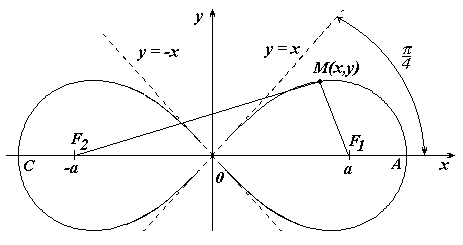 емниската Бернулли
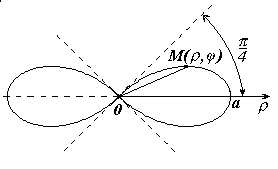
емниската Бернулли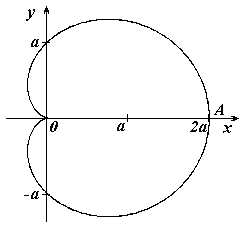 ардиоида
ардиоида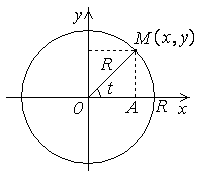 - параметрические
- параметрические 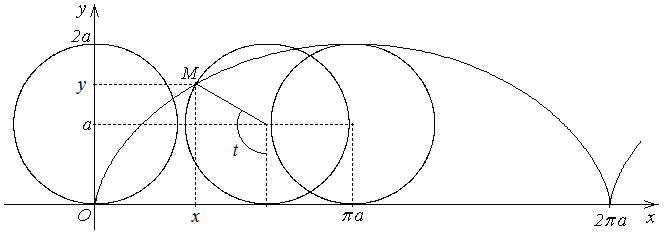 иклоида
иклоида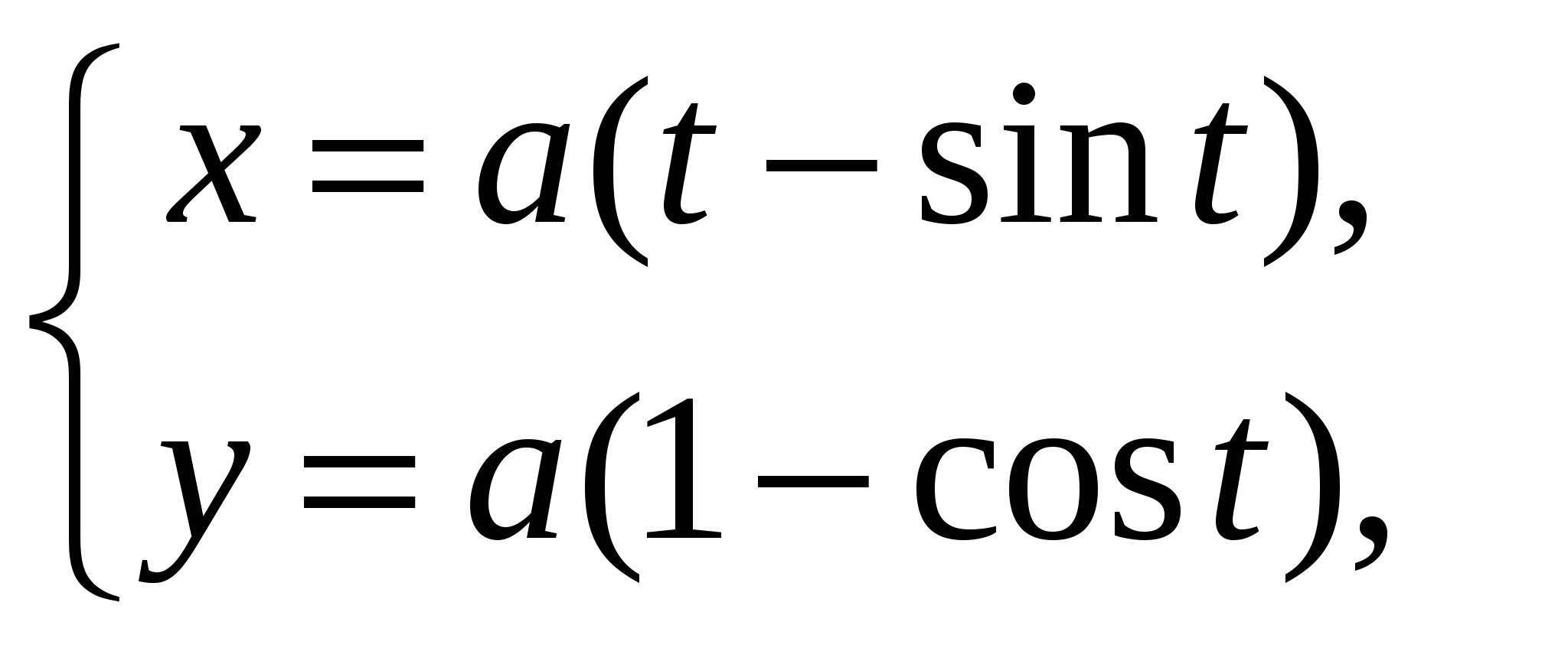 где
где 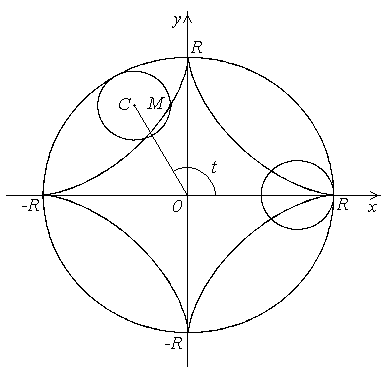 ри
ри 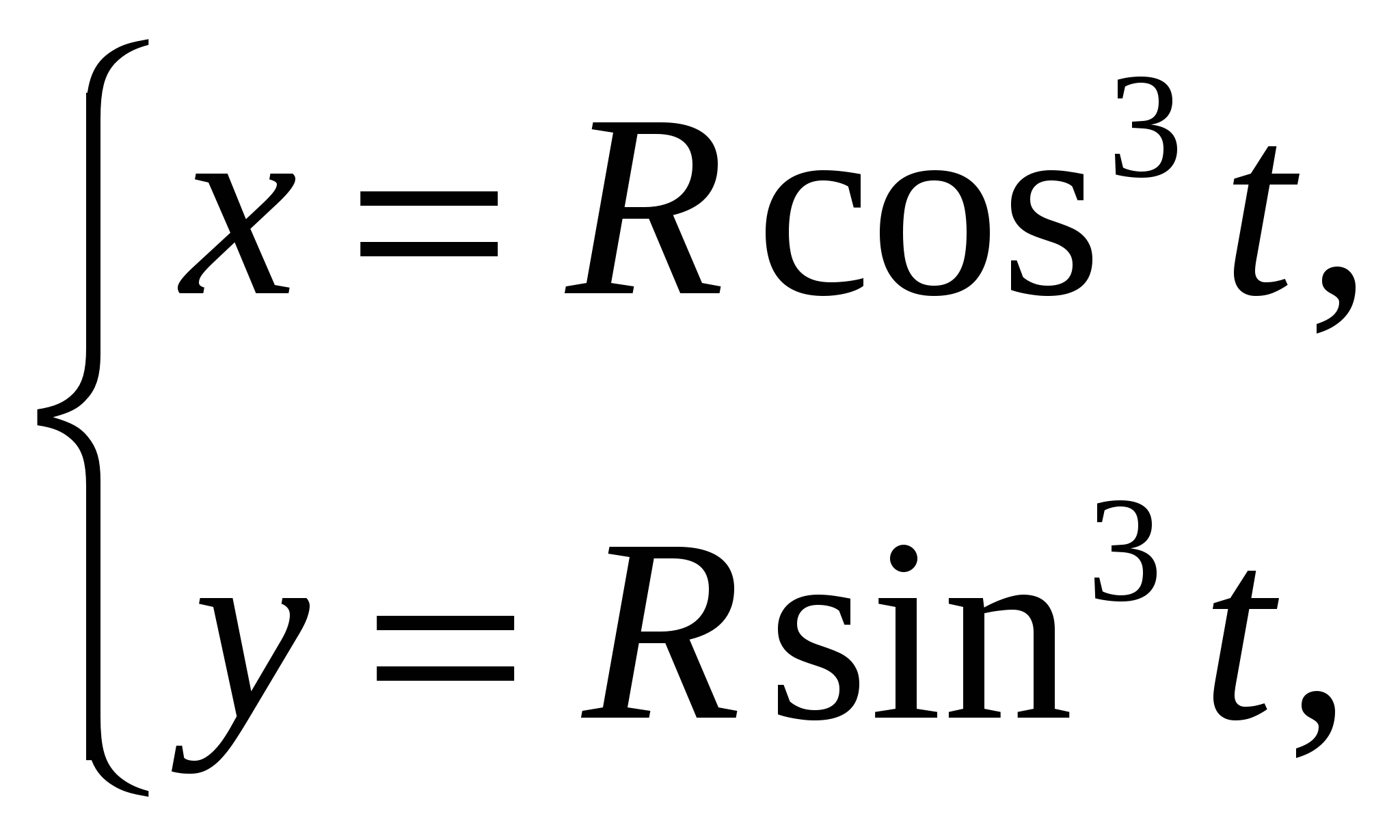 где
где