Плоскость в пространстве
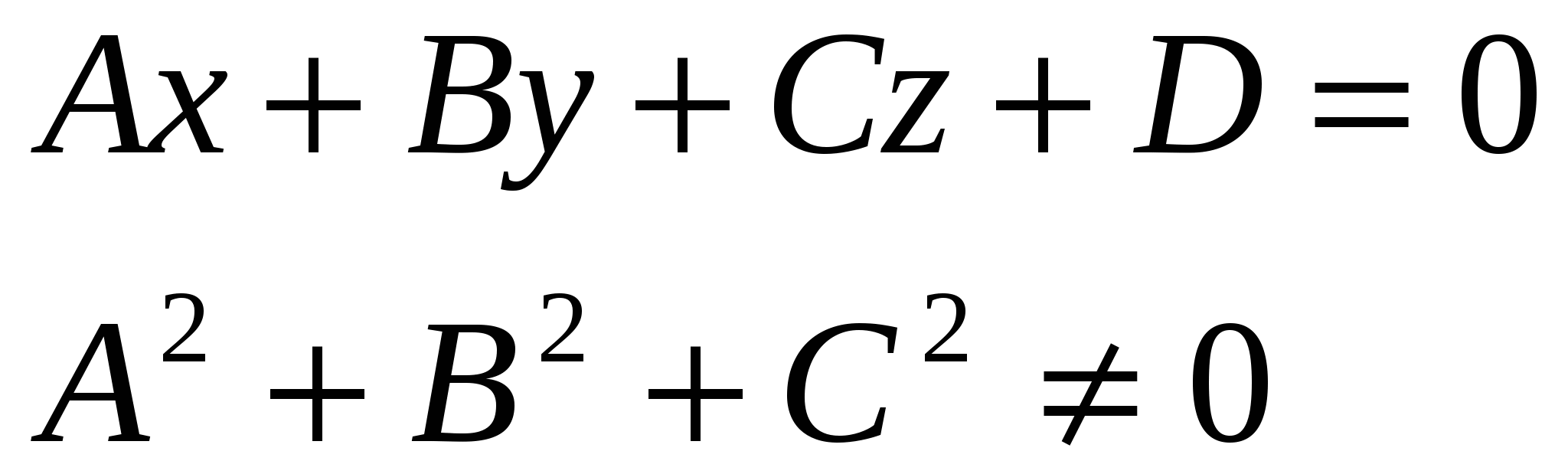 - общее уравнение плоскости в декартовой системе - общее уравнение плоскости в декартовой системе
координат;
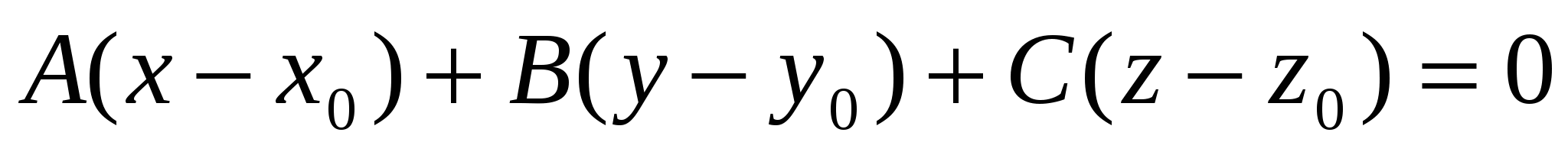 - уравнение плоскости, проходящей через заданную точку - уравнение плоскости, проходящей через заданную точку 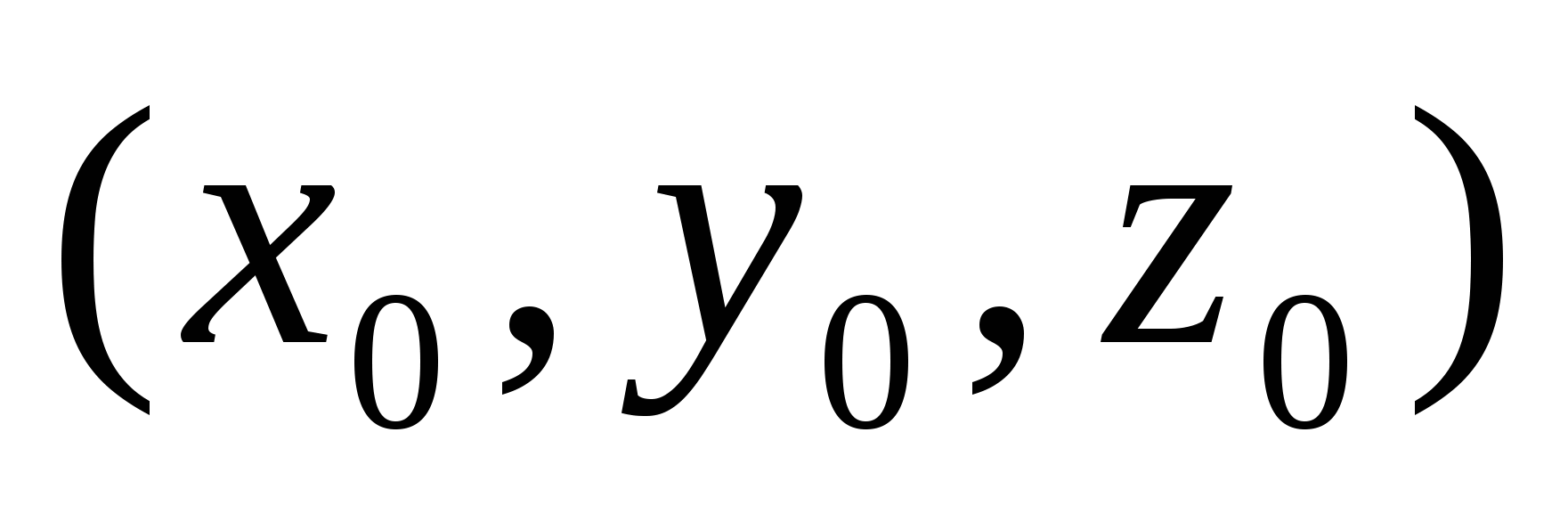 и перпендикулярной вектору и перпендикулярной вектору 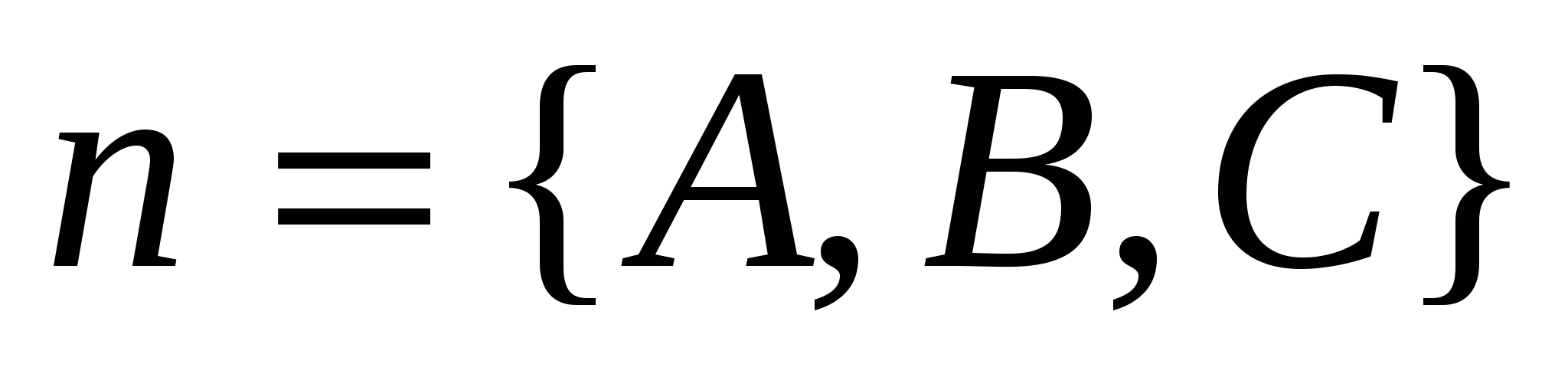 ; ;
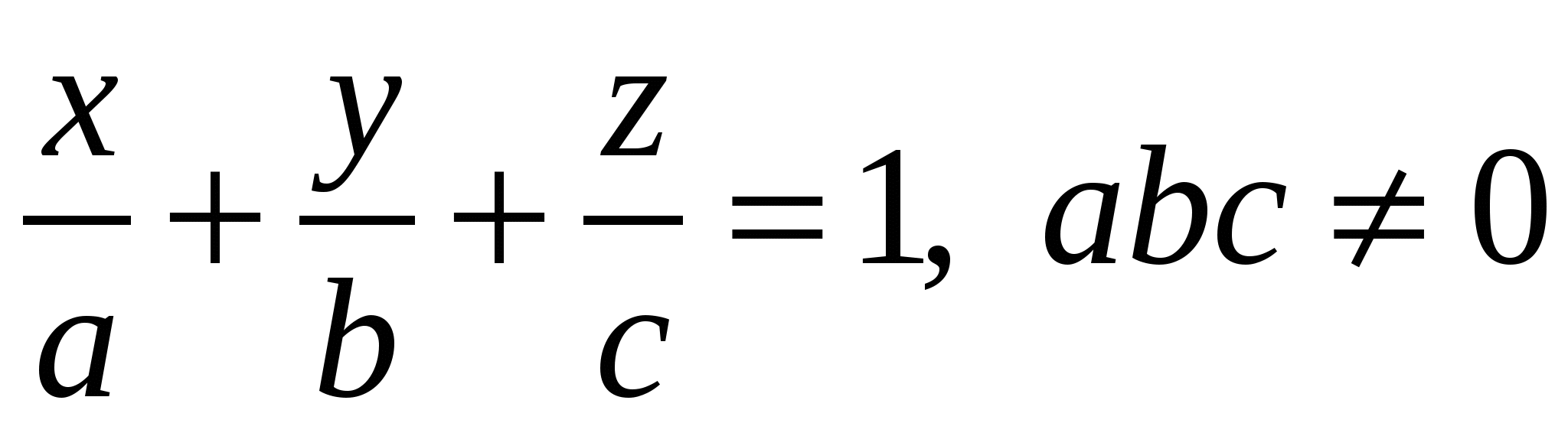 - уравнение плоскости, отсекающей на осях координат - уравнение плоскости, отсекающей на осях координат 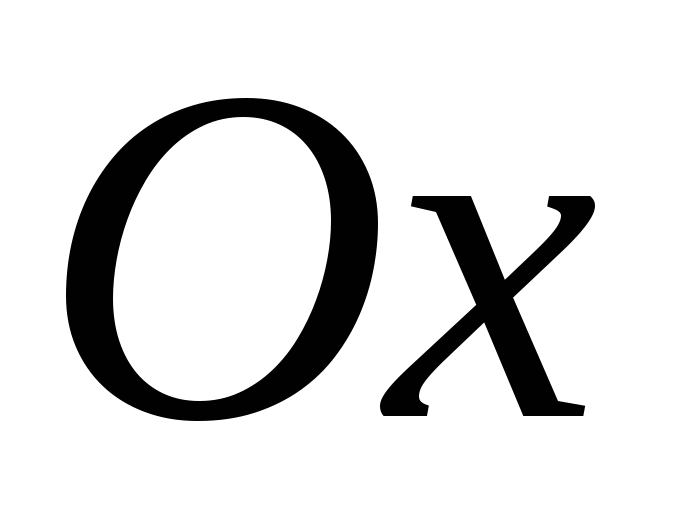 , , 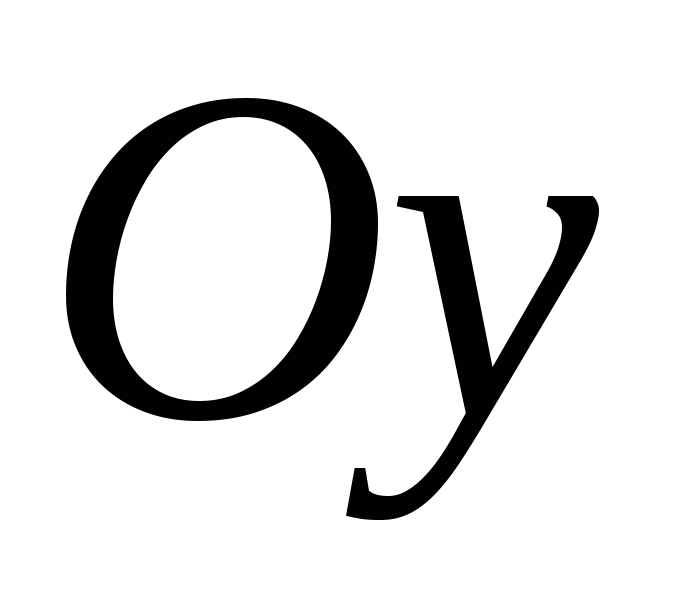 , ,  отрезки a, b и c соответственно; отрезки a, b и c соответственно;
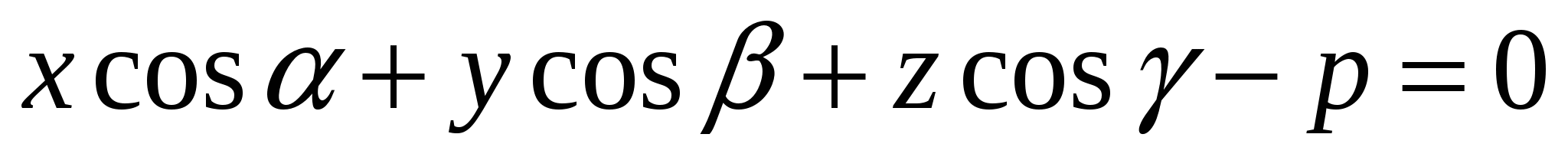 - нормальное уравнение плоскости, где - нормальное уравнение плоскости, где
р – расстояние от начала координат до плоскости, а единичный вектор, перпендикулярный плоскости, имеет координаты 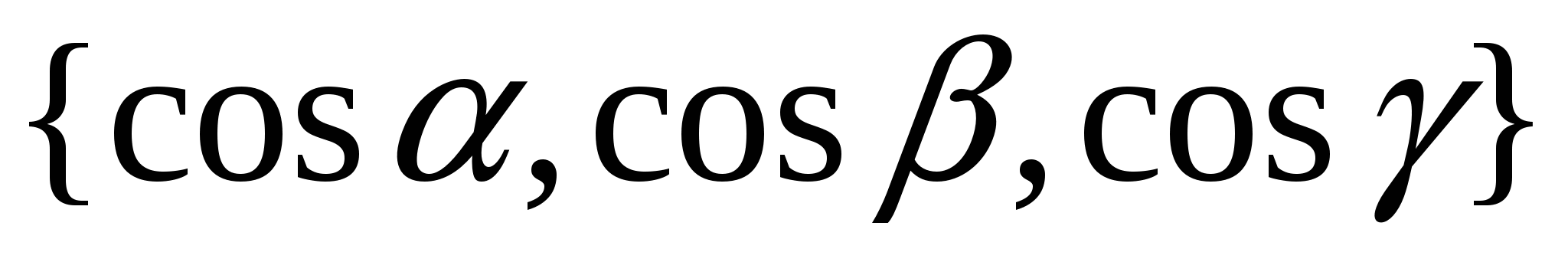 ; ;
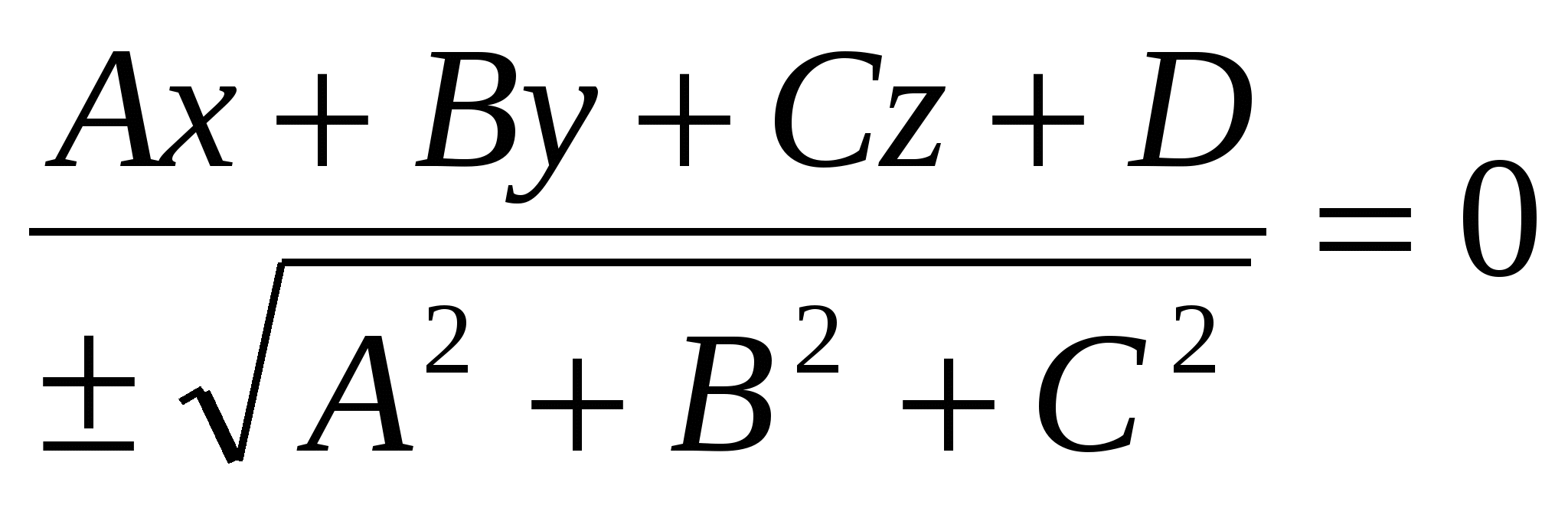 - нормальный вид общего уравнения плоскости (знак нормирующего множителя противоположен знаку D); - нормальный вид общего уравнения плоскости (знак нормирующего множителя противоположен знаку D);
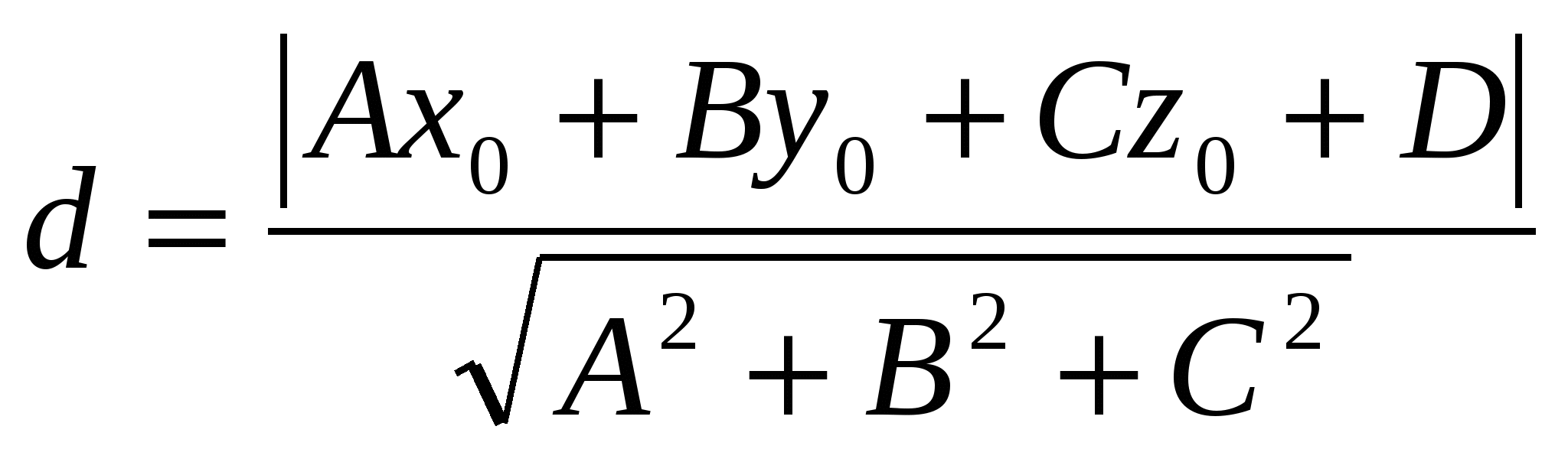 - расстояние от точки - расстояние от точки 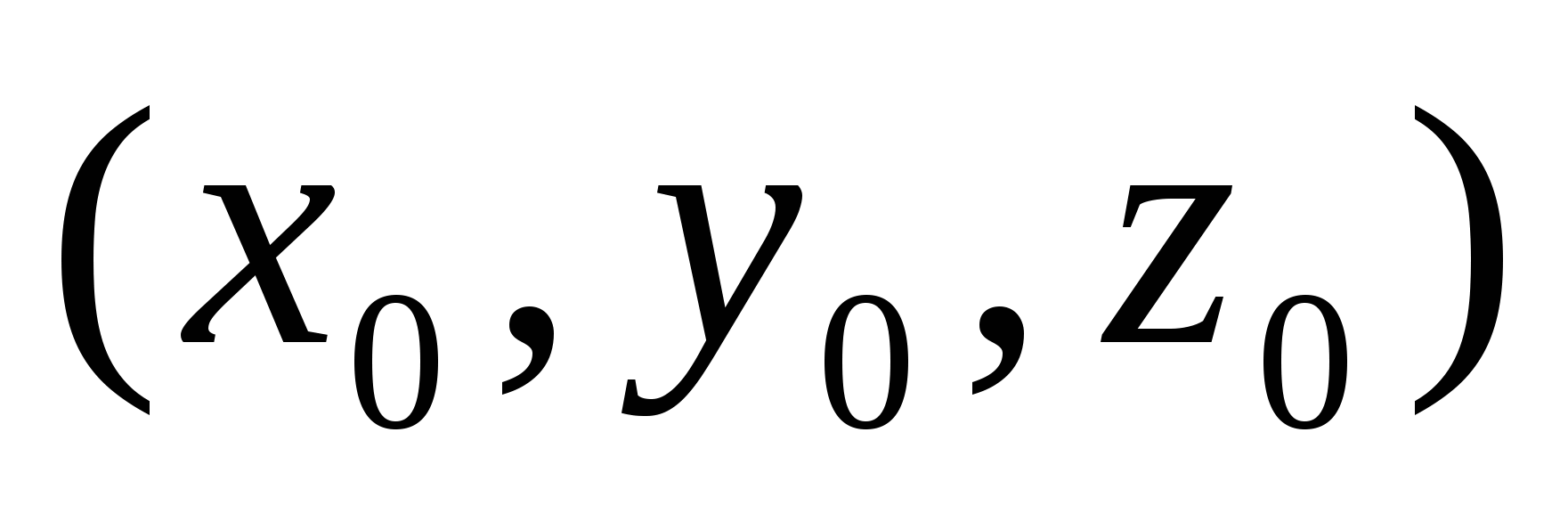 до плоскости, заданной общим уравнением; до плоскости, заданной общим уравнением;
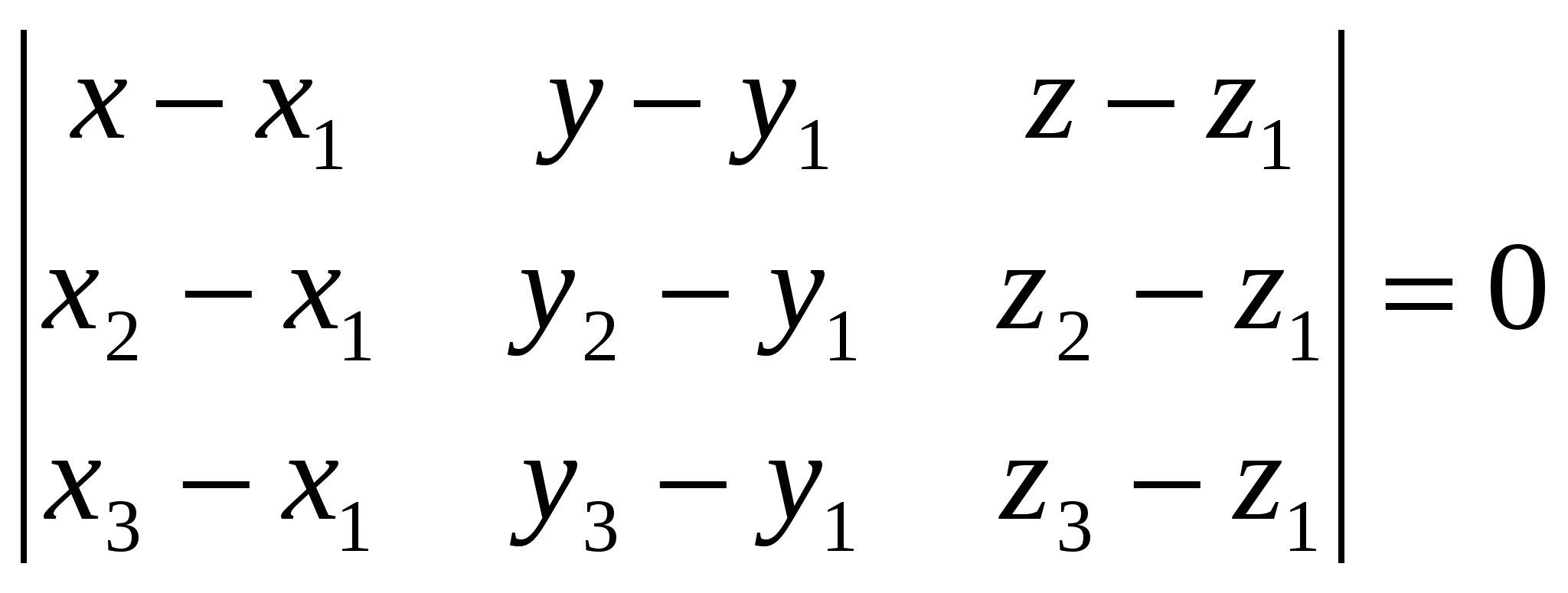 - уравнение плоскости, проходящей через три точки - уравнение плоскости, проходящей через три точки 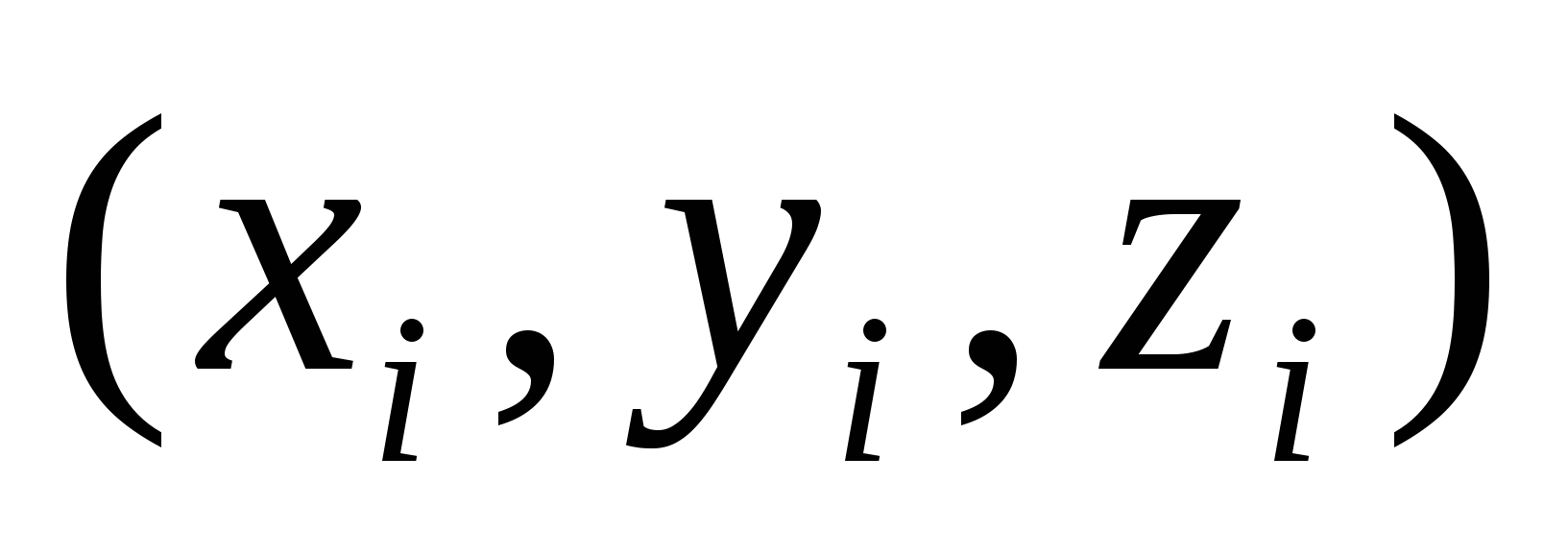 (i=1,2,3), не лежащие на одной прямой; (i=1,2,3), не лежащие на одной прямой;
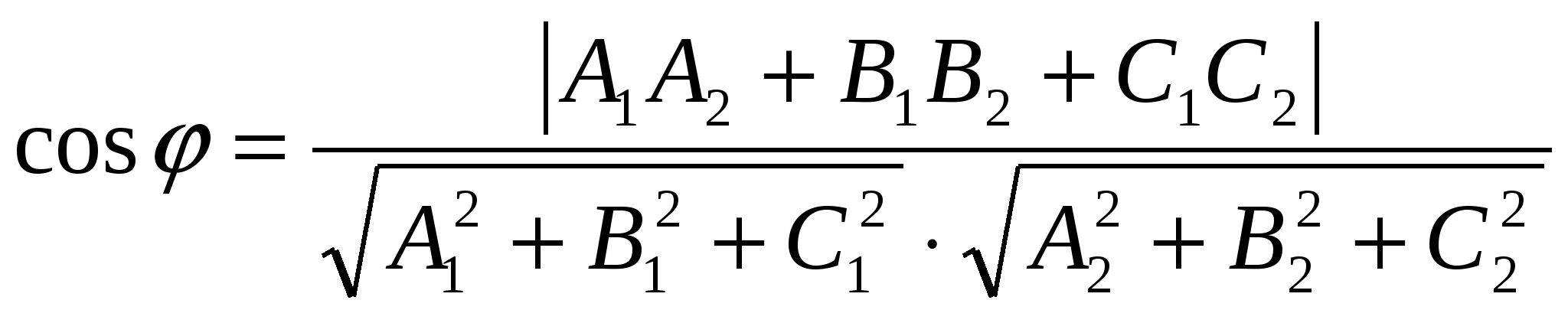 - угол - угол  между плоскостями между плоскостями 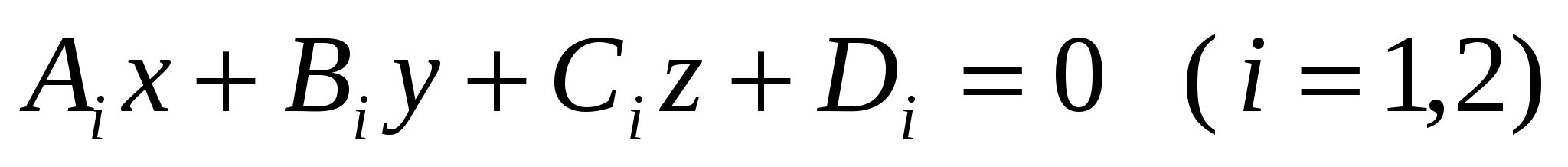 ; ;
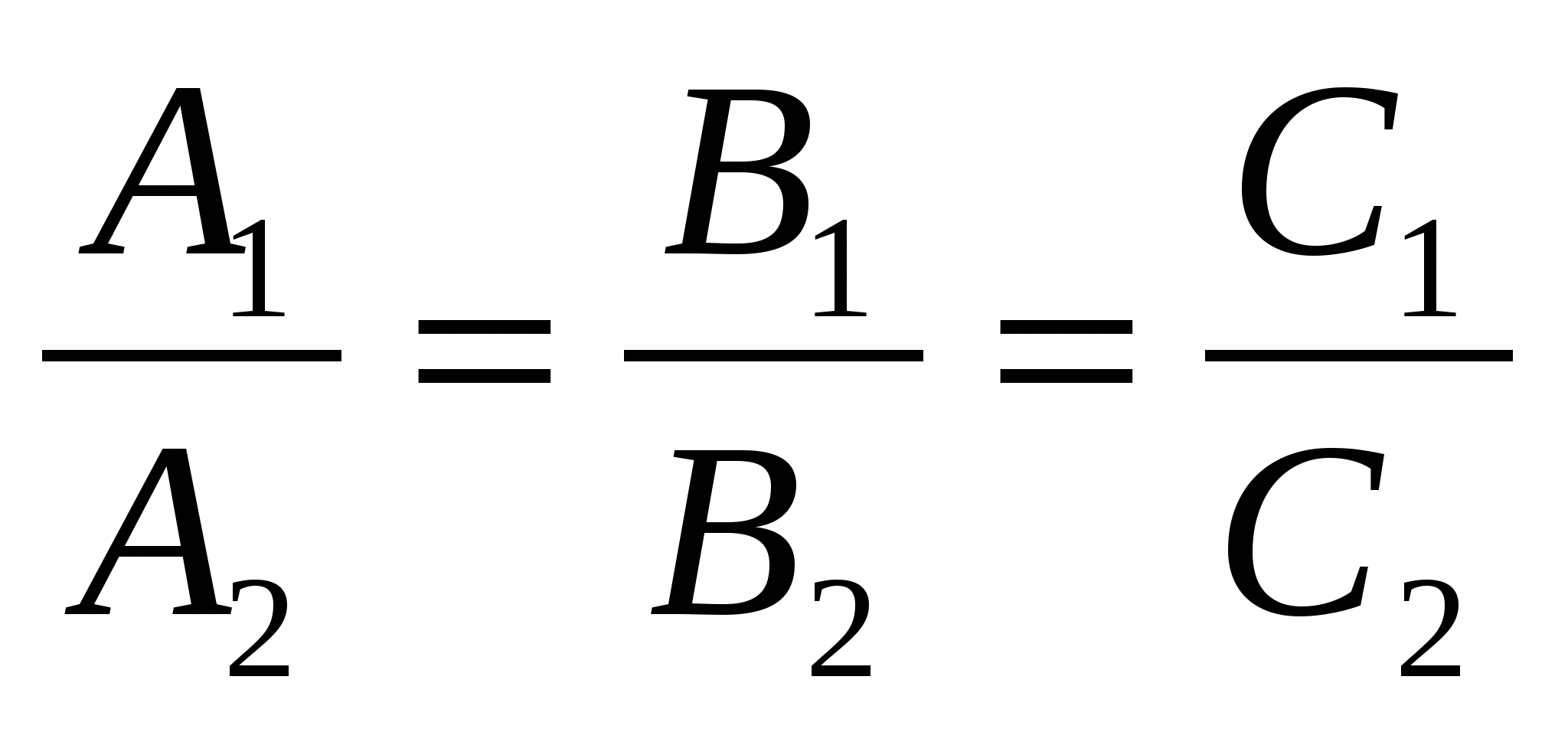 - необходимое и достаточное условие параллельности плоскостей - необходимое и достаточное условие параллельности плоскостей 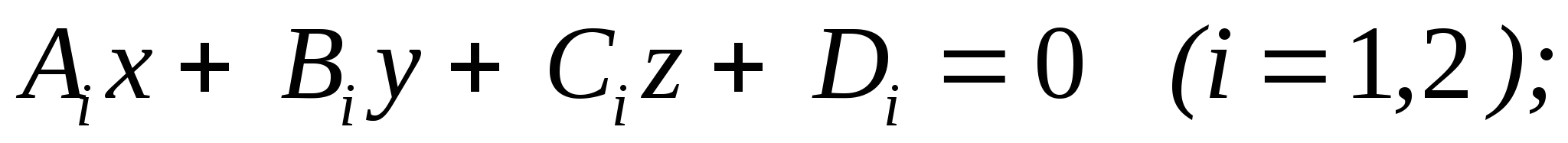
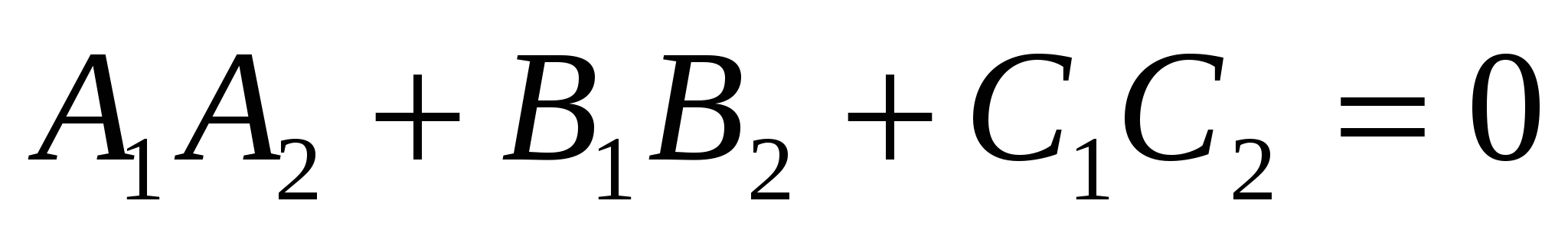 - необходимое и достаточное условие перпендикулярности плоскостей - необходимое и достаточное условие перпендикулярности плоскостей 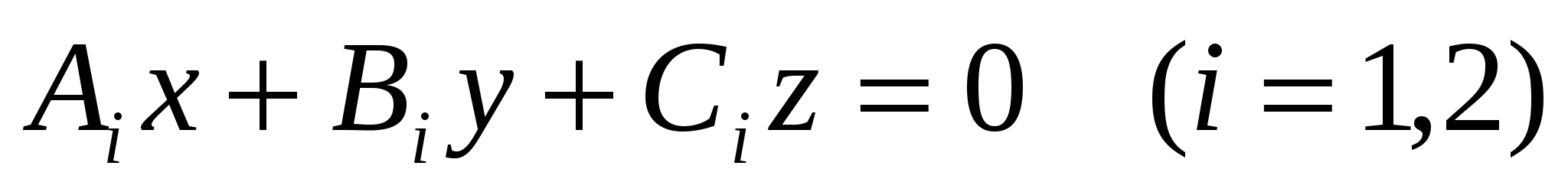 ; ;
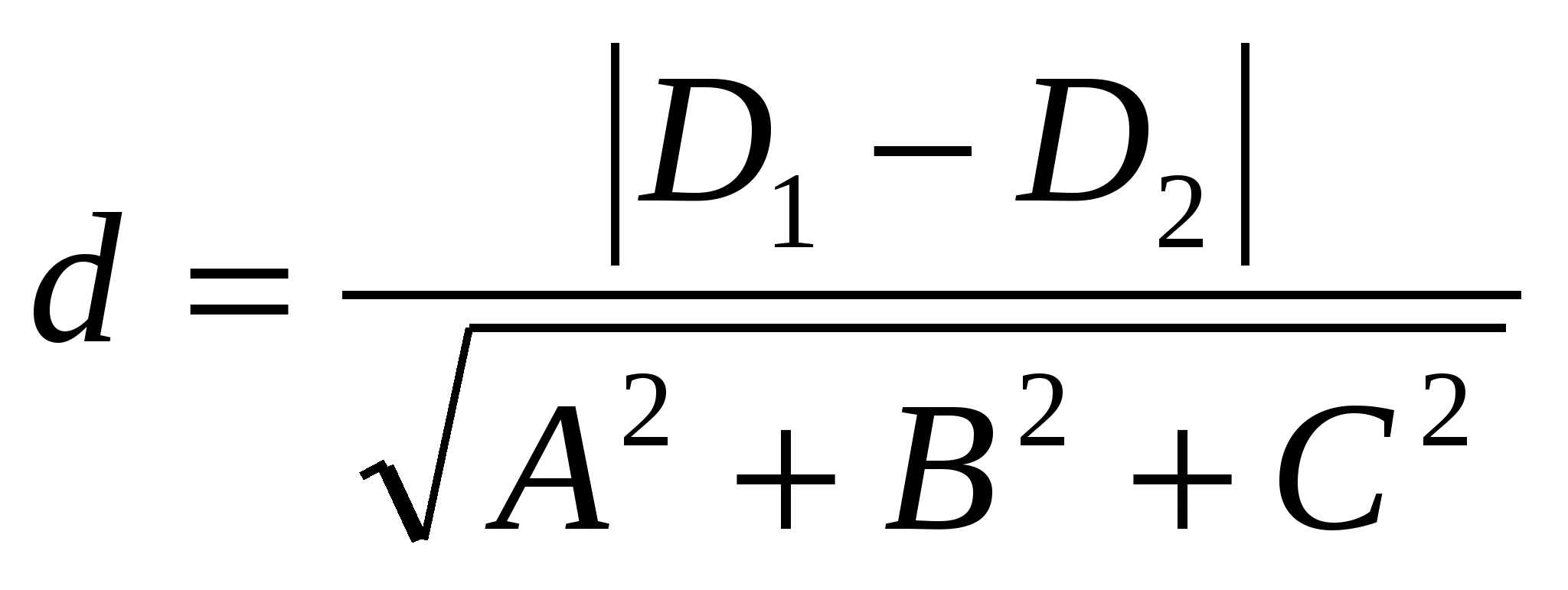 - расстояние между двумя параллельными плоскостями - расстояние между двумя параллельными плоскостями 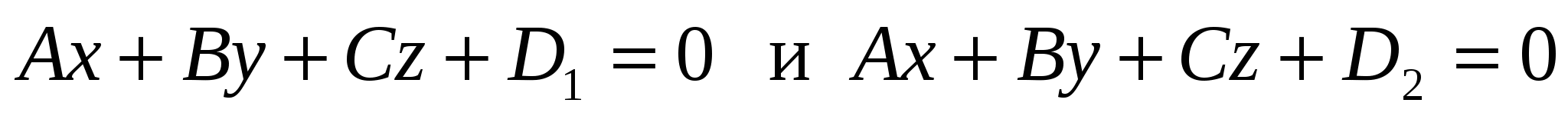 . .
Прямая в пространстве
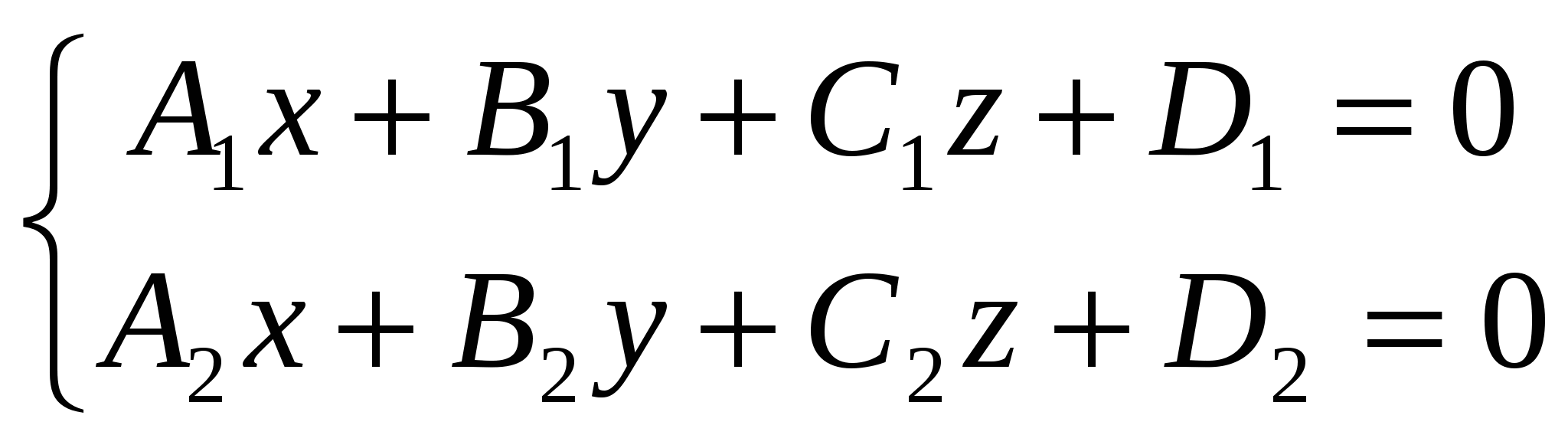 - общее уравнение прямой как линии пересечения двух параллельных плоскостей; - общее уравнение прямой как линии пересечения двух параллельных плоскостей;
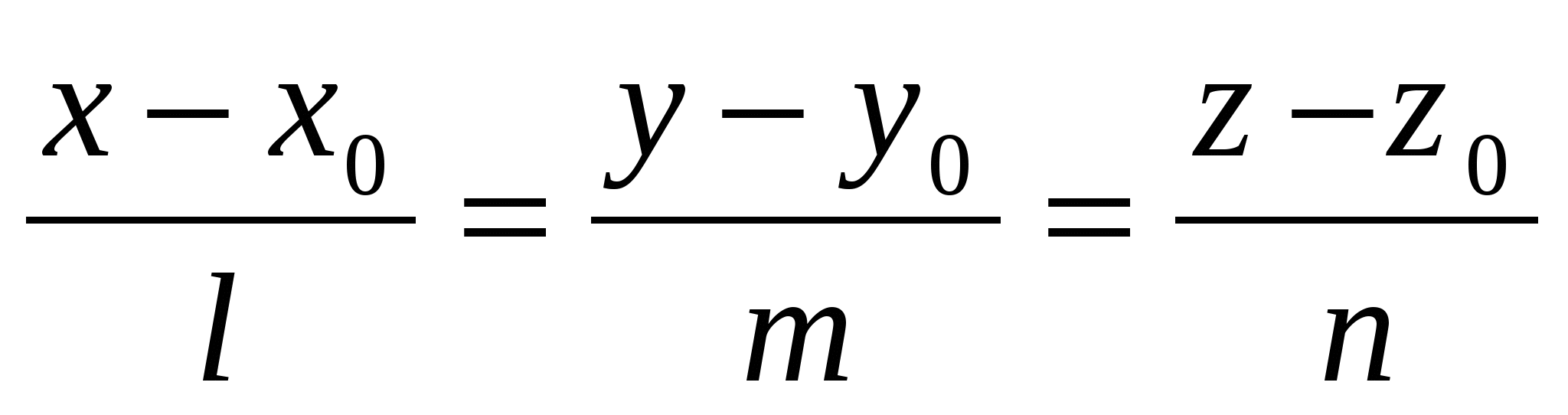 - канонические уравнения прямой, проходящей через точку - канонические уравнения прямой, проходящей через точку 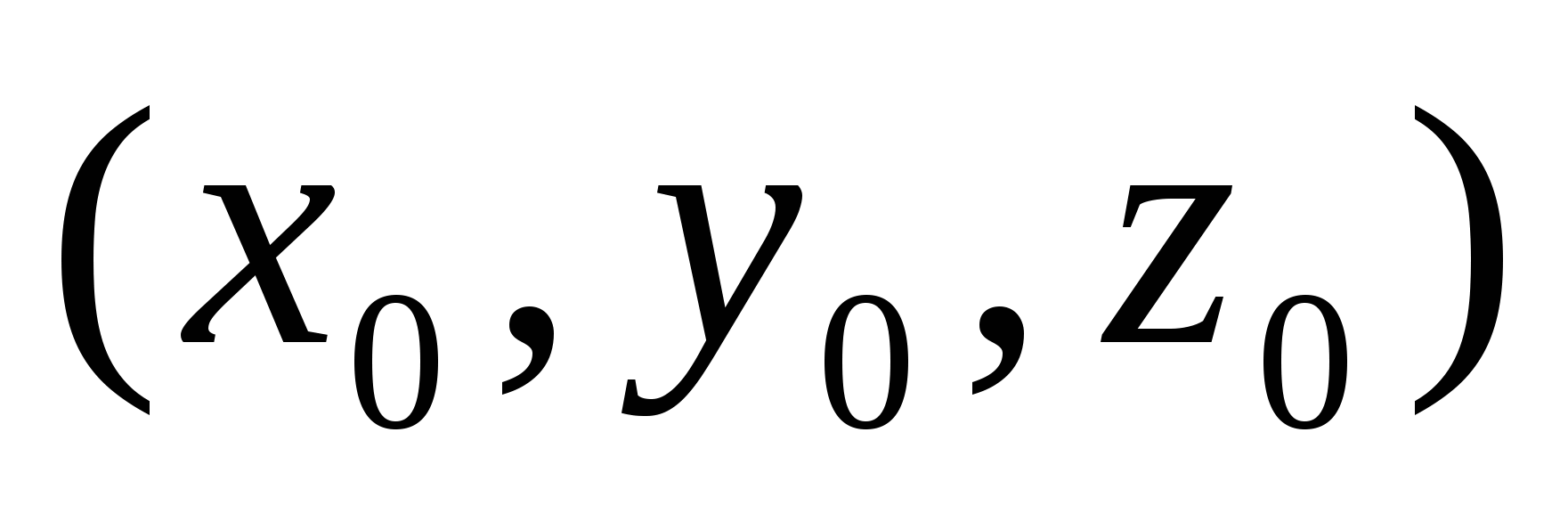 и имеющей направляющий вектор с компонентами и имеющей направляющий вектор с компонентами 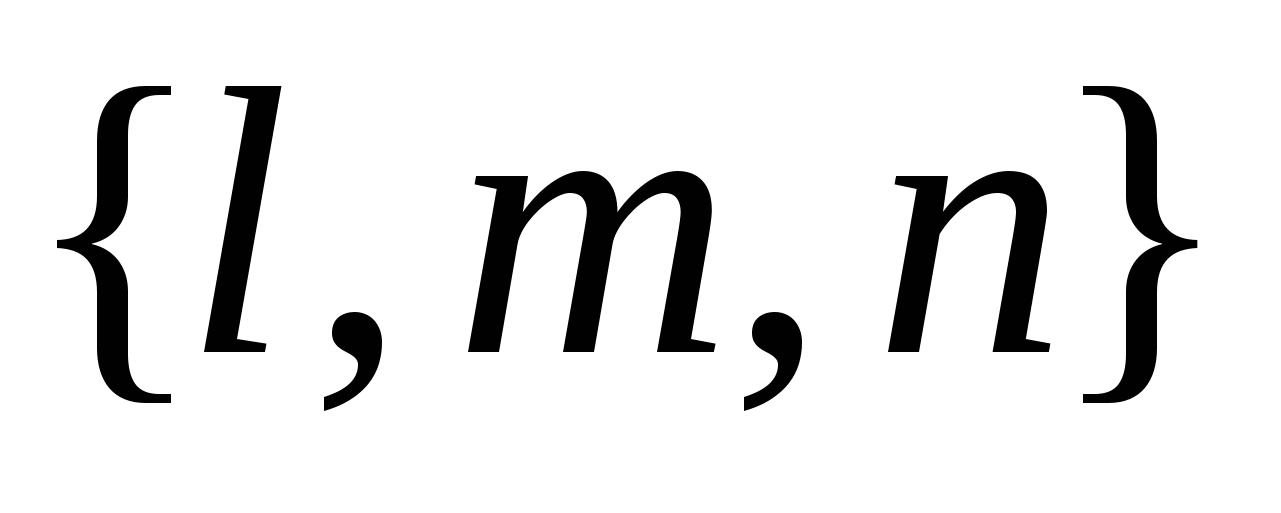 ; ;
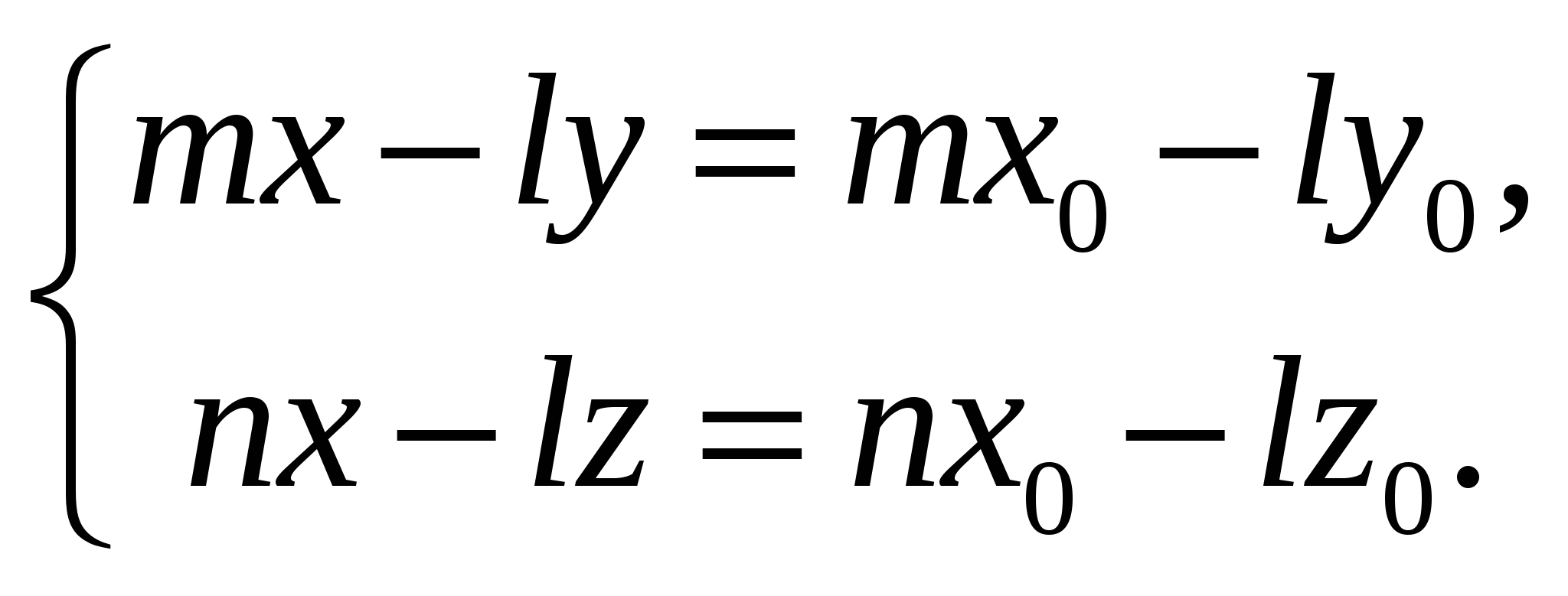 - уравнения прямой в виде проекций на координатные плоскости; - уравнения прямой в виде проекций на координатные плоскости;
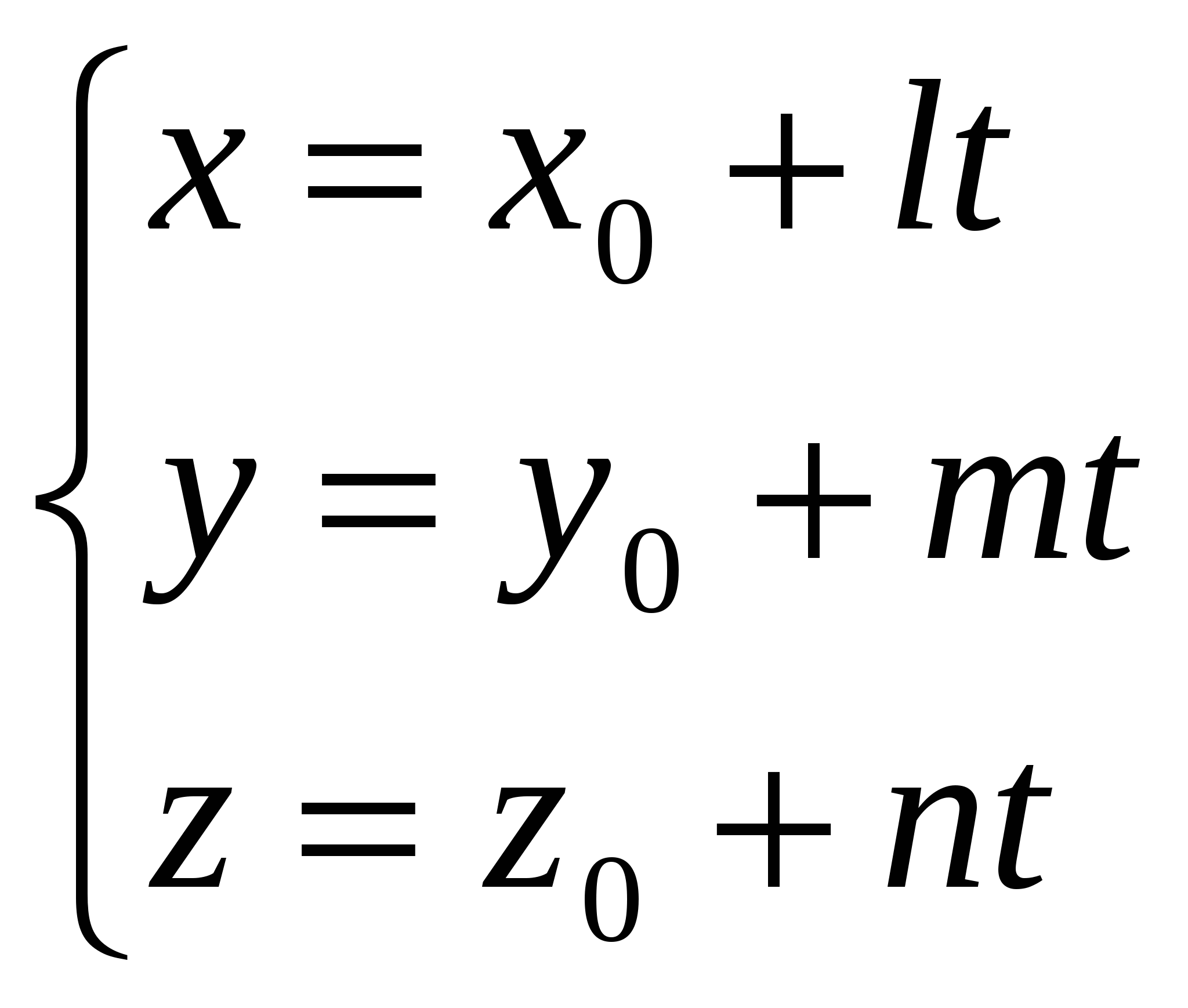 - параметрические уравнения прямой, проходящей через точку - параметрические уравнения прямой, проходящей через точку 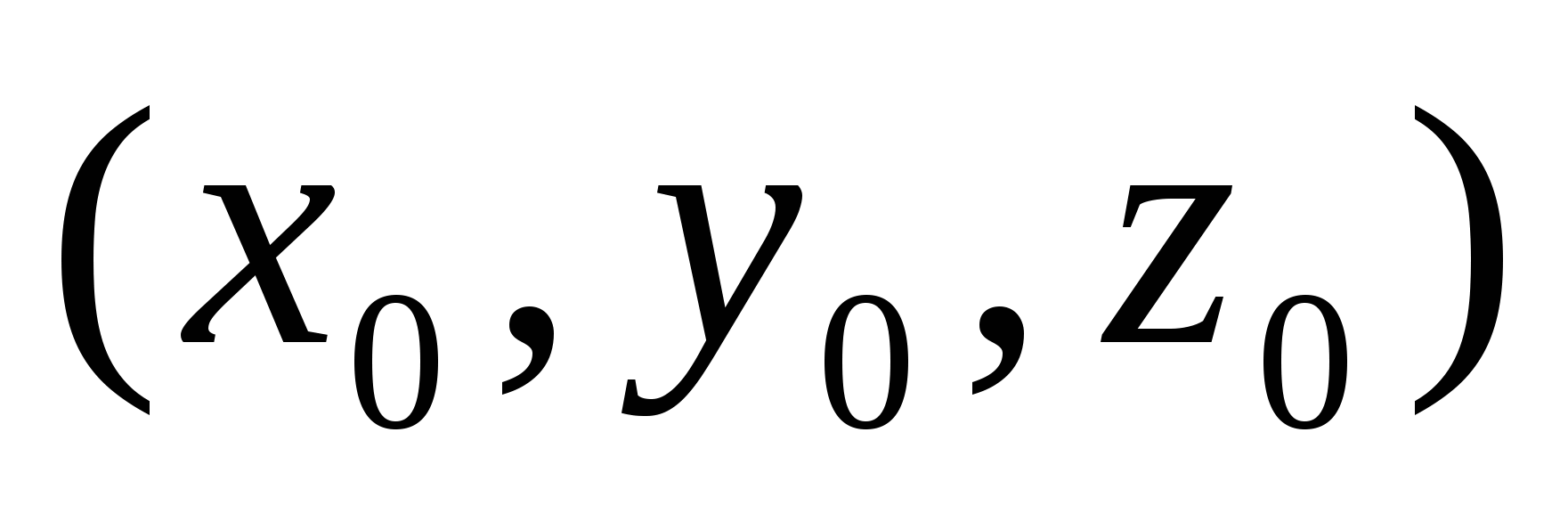 и имеющей направляющий вектор с компонентами и имеющей направляющий вектор с компонентами 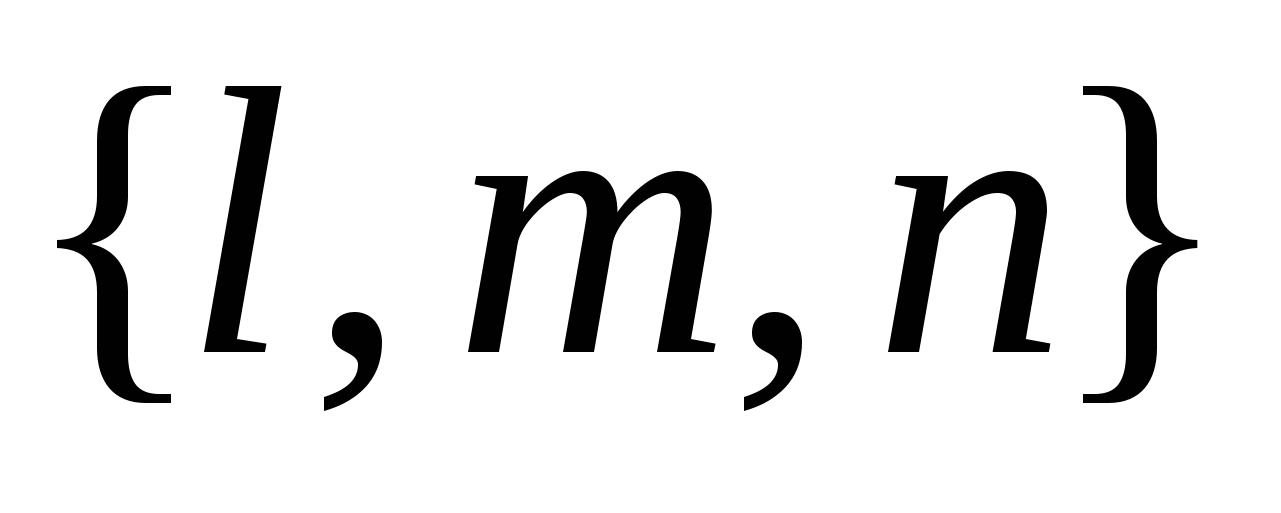 ; ;
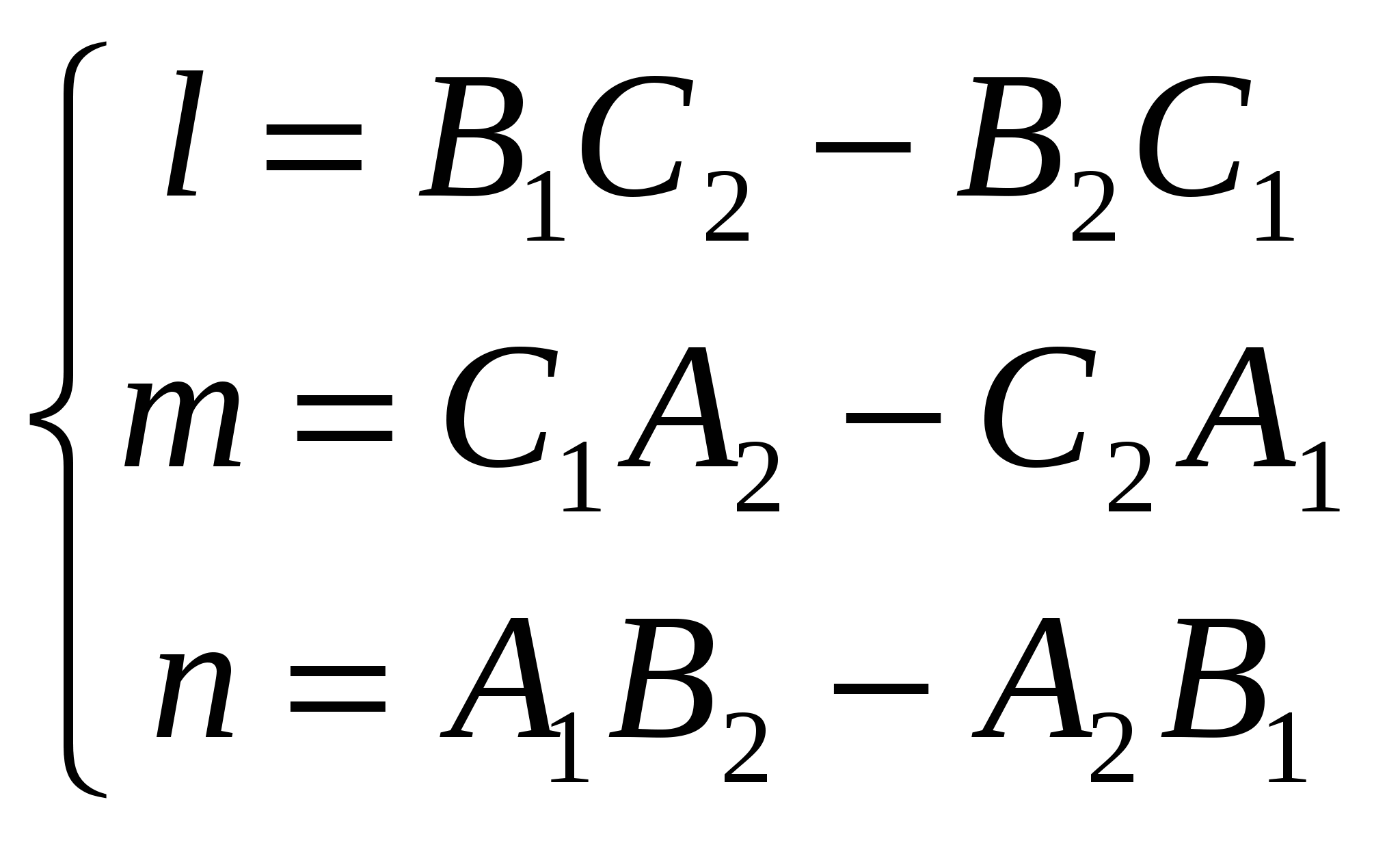 - соотношения между компонентами направляющего вектора прямой и координатами общего уравнения прямой; - соотношения между компонентами направляющего вектора прямой и координатами общего уравнения прямой;
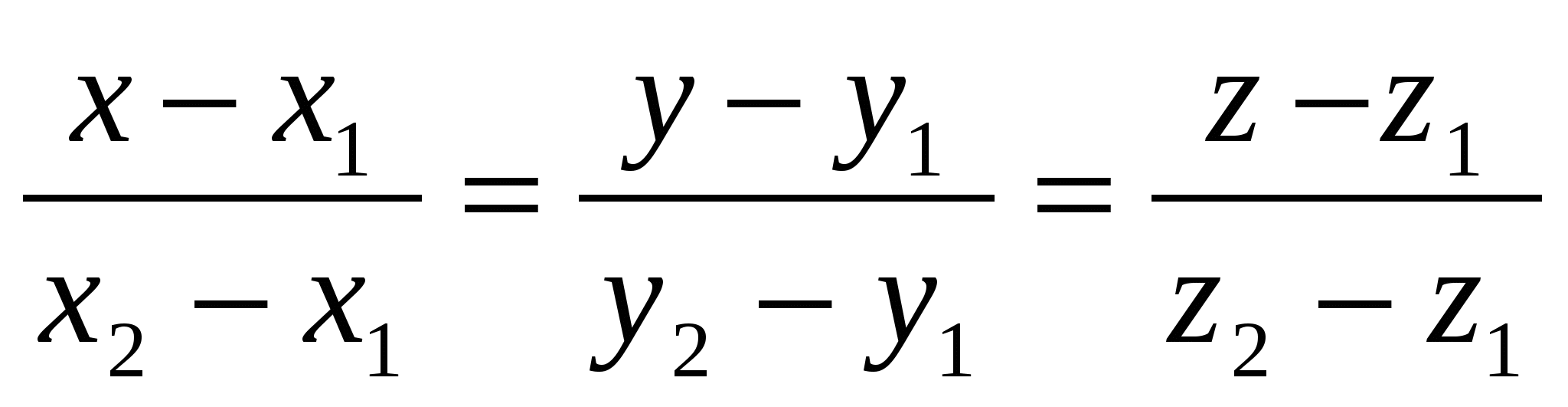 - канонические уравнения прямой, проходящей через точки с координатами - канонические уравнения прямой, проходящей через точки с координатами 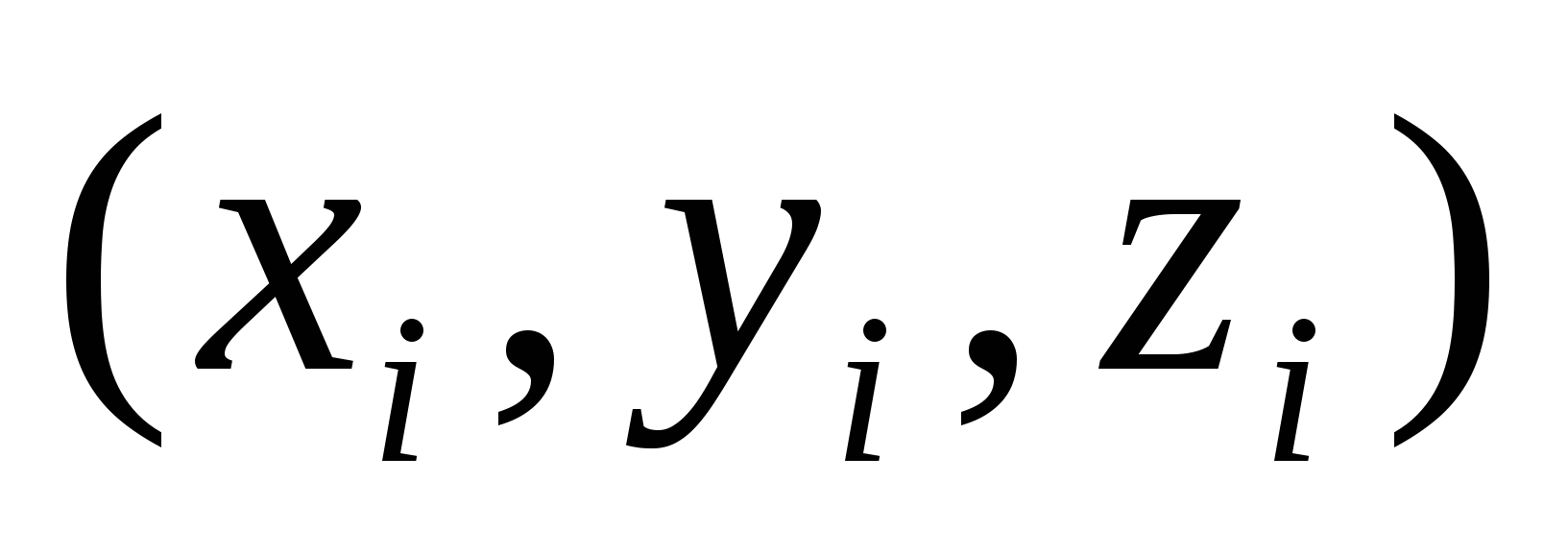 ( (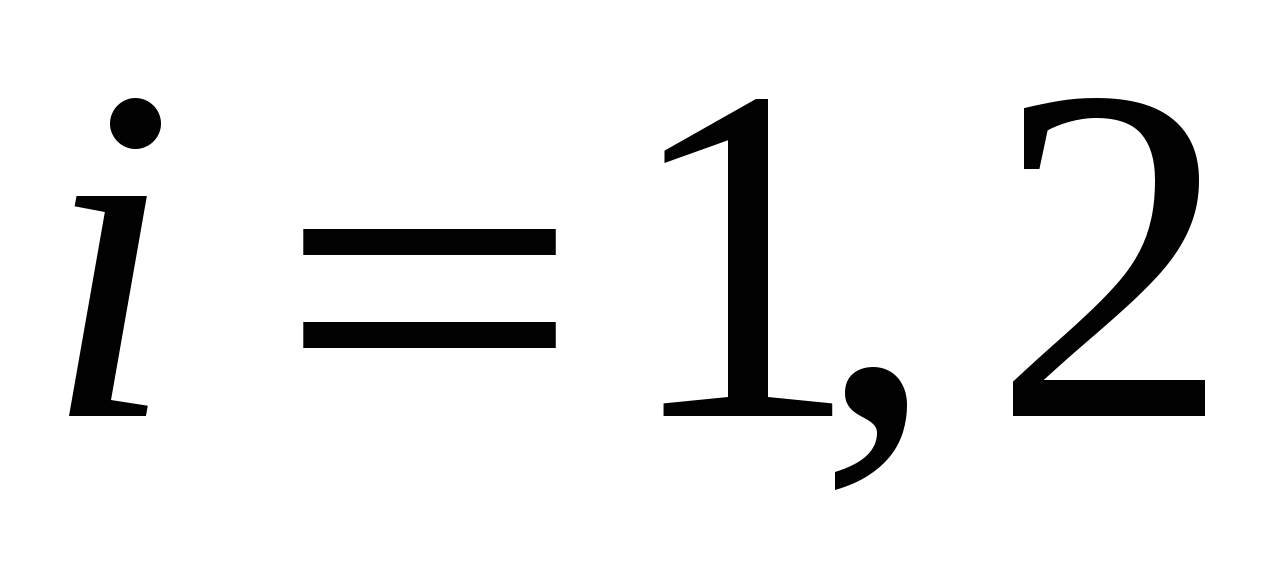 ); );
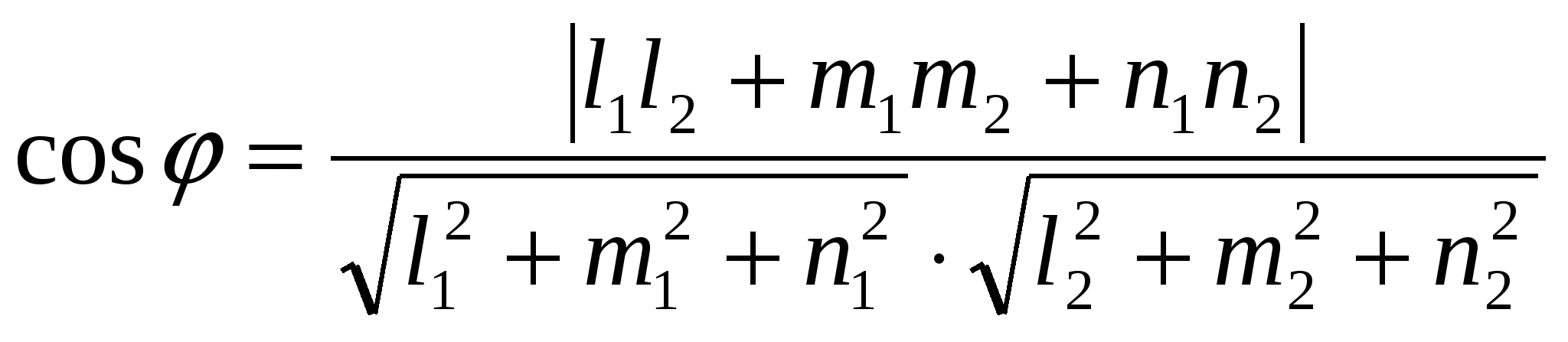 - косинус угла - косинус угла  между прямыми между прямыми 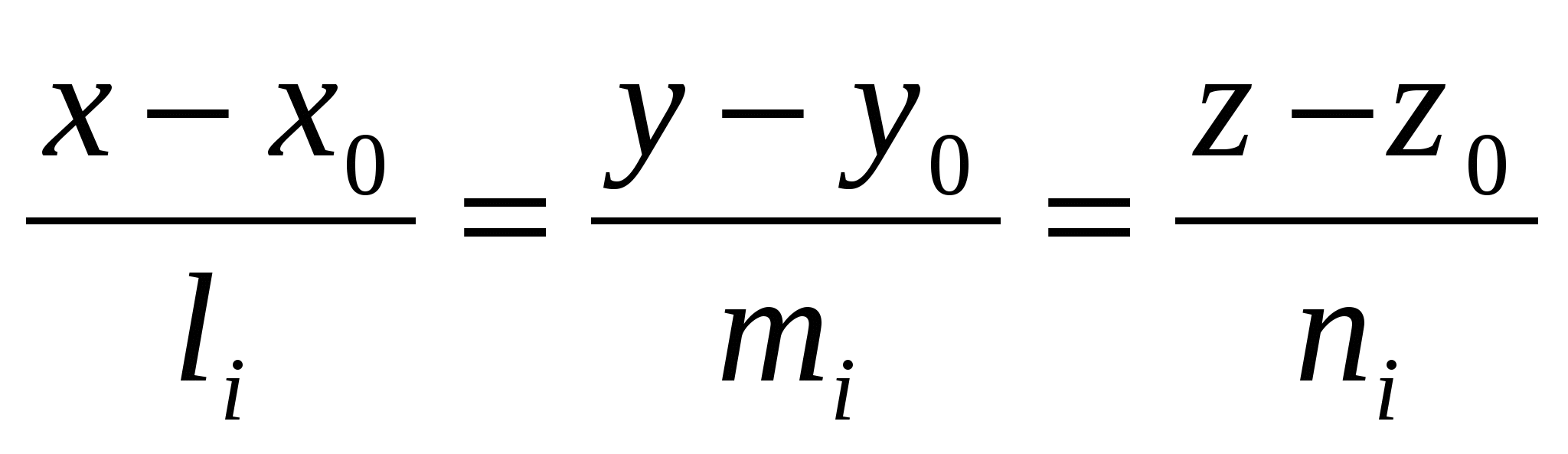 ( (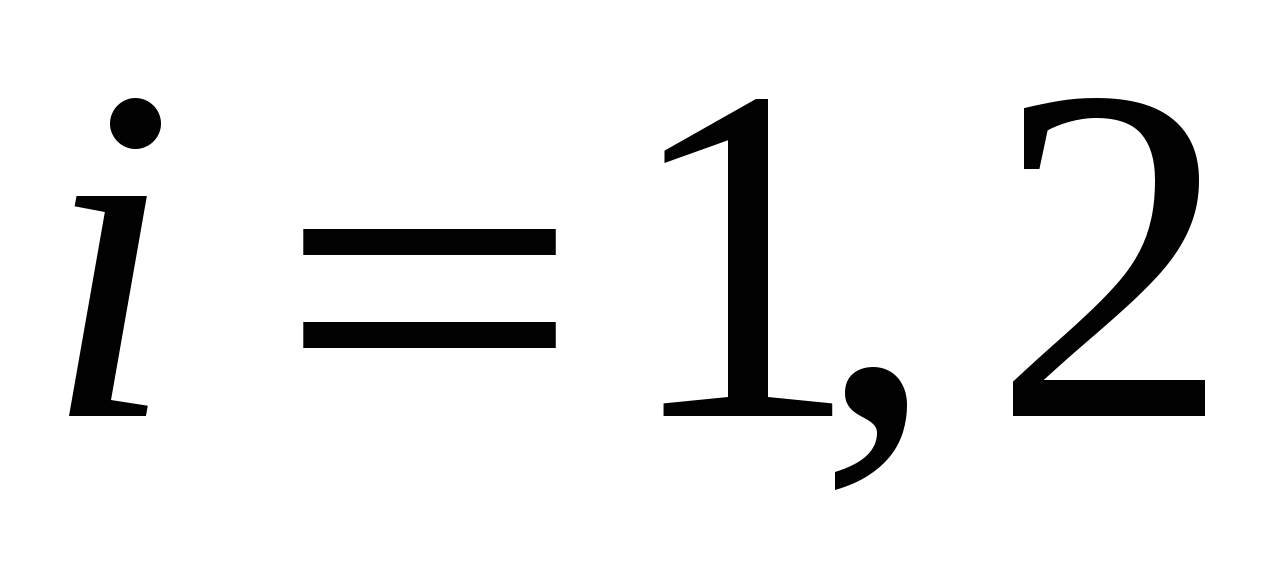 ), проходящими через точку ), проходящими через точку 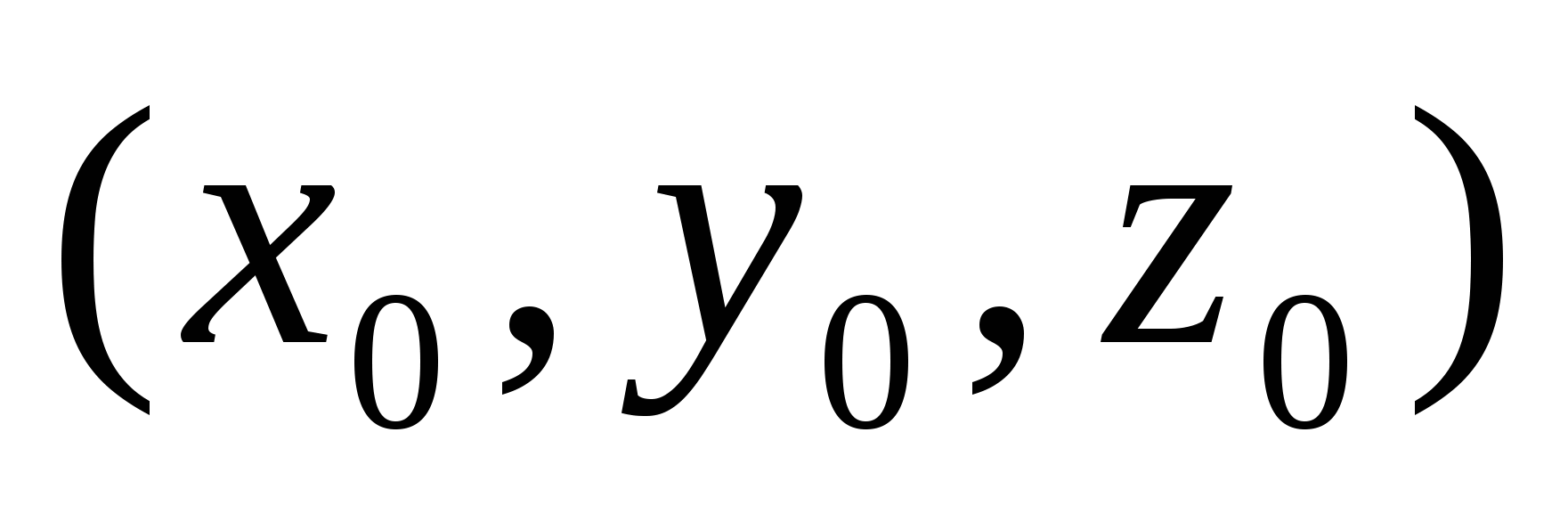 ; ;
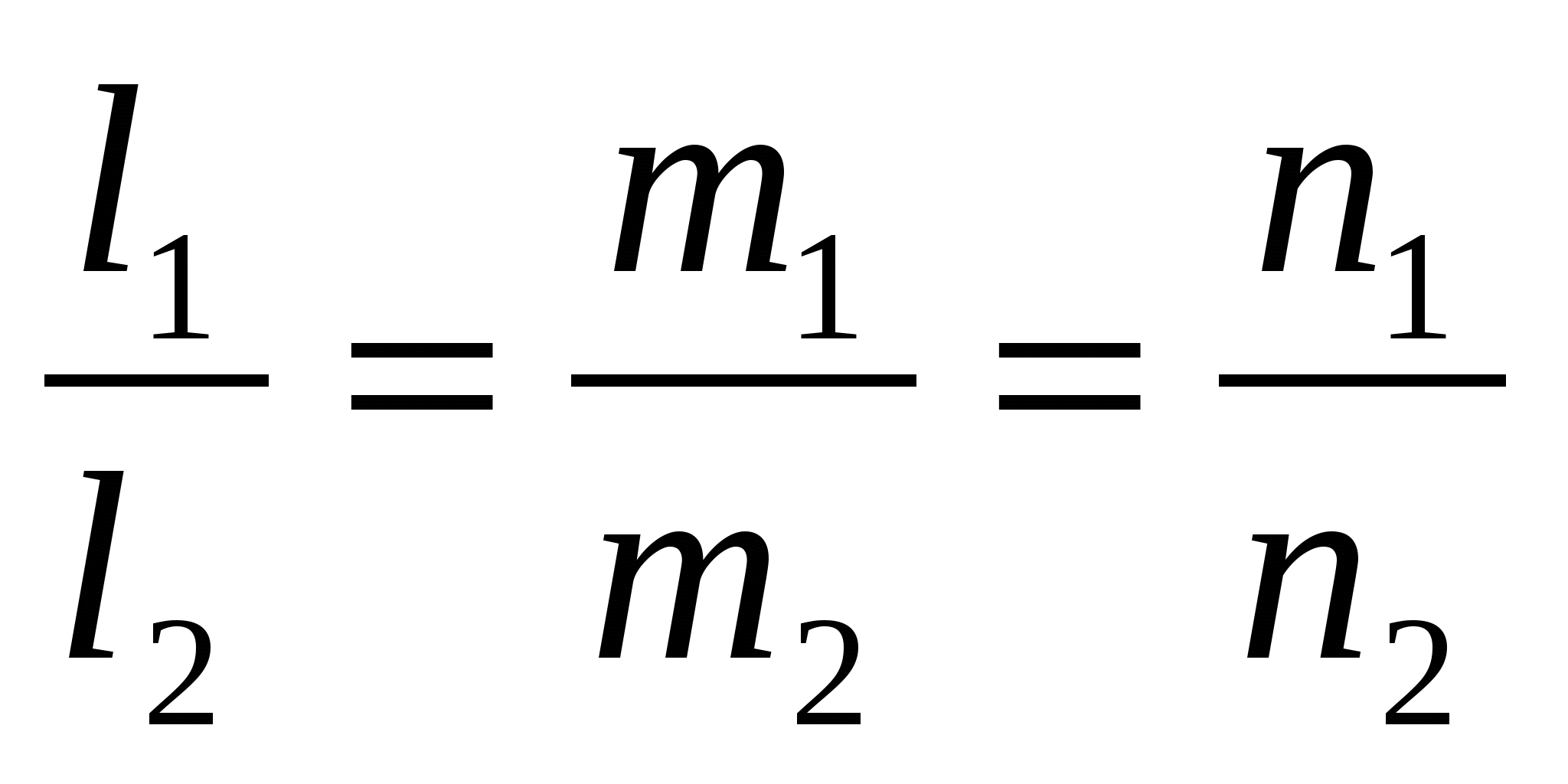 - условие параллельности двух прямых - условие параллельности двух прямых 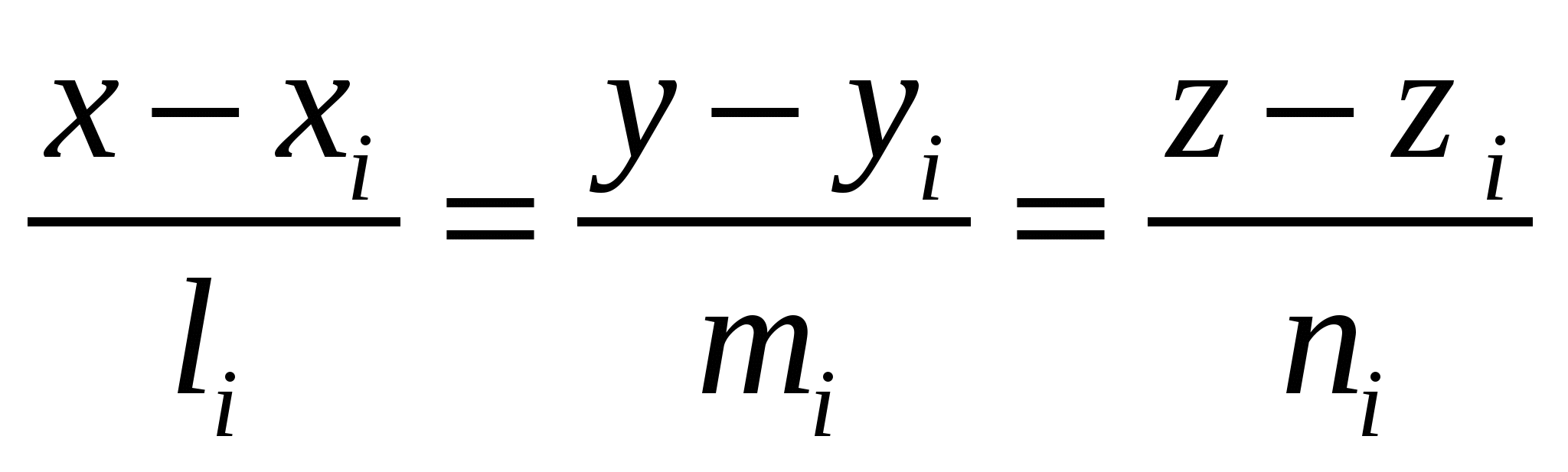 ( (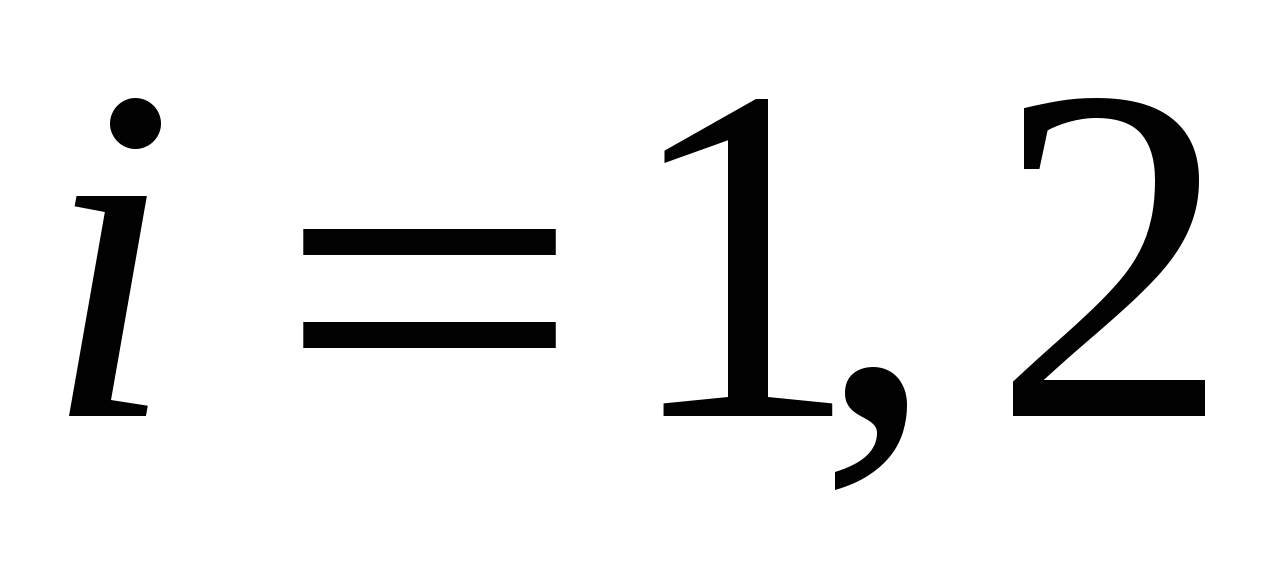 ); );
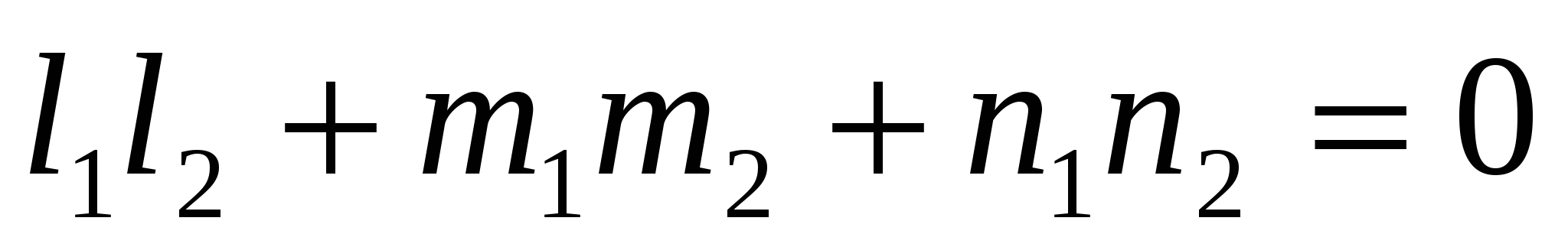 - условие перпендикулярности двух прямых - условие перпендикулярности двух прямых 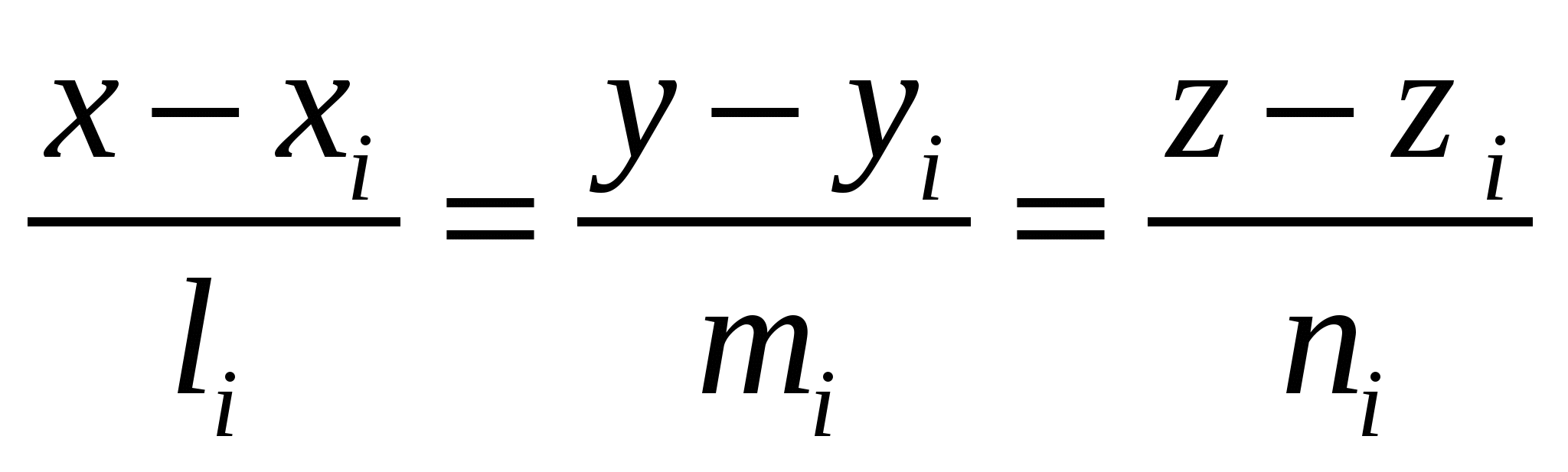 ( (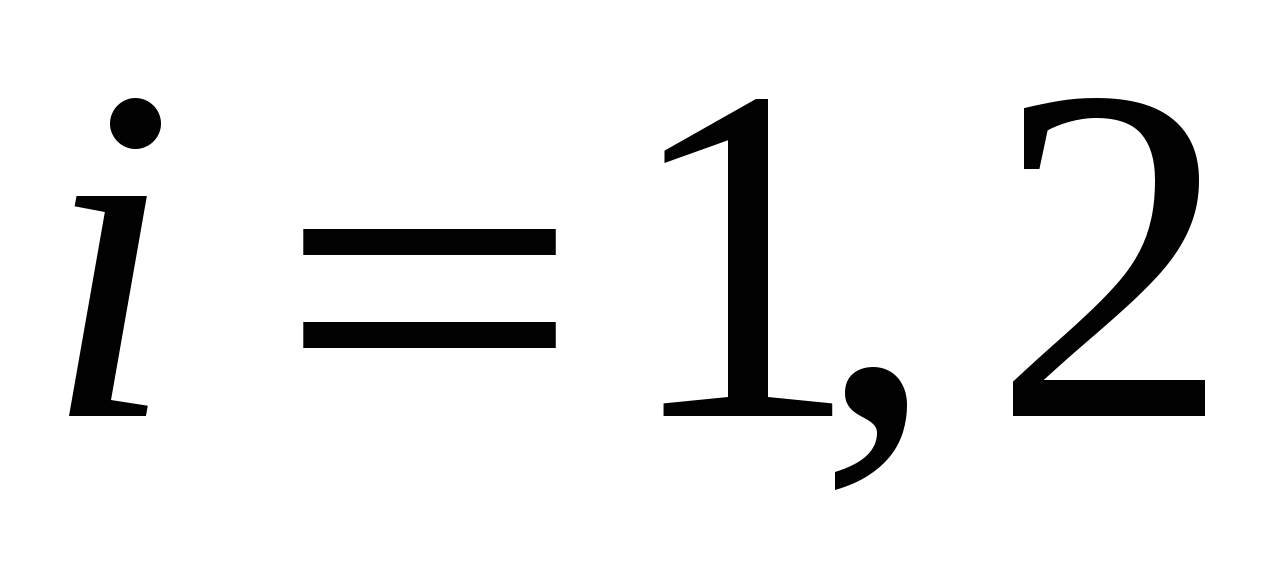 ); );
Прямые: 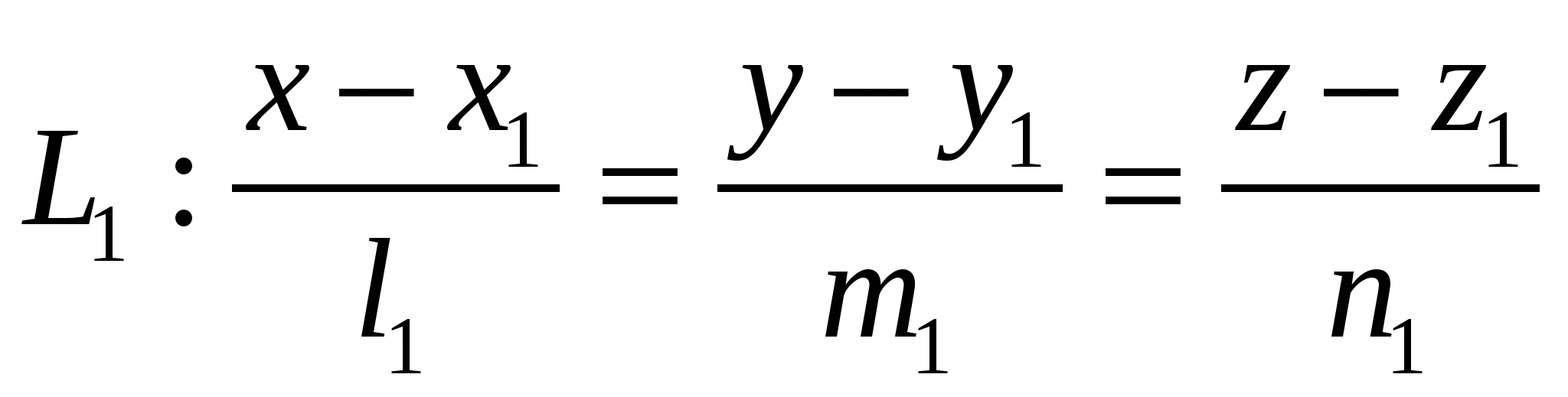 и и 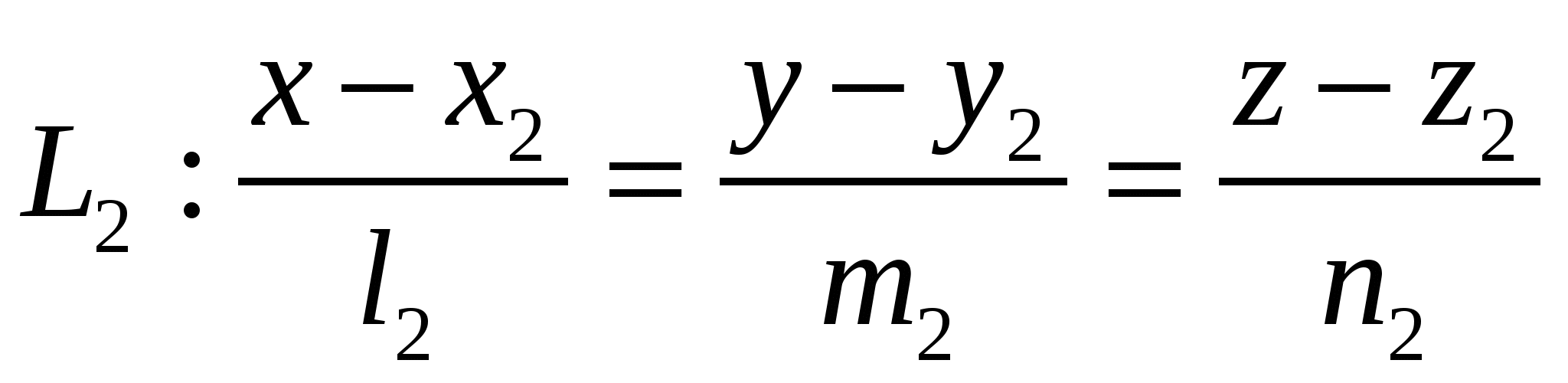 лежат в одной плоскости, если лежат в одной плоскости, если
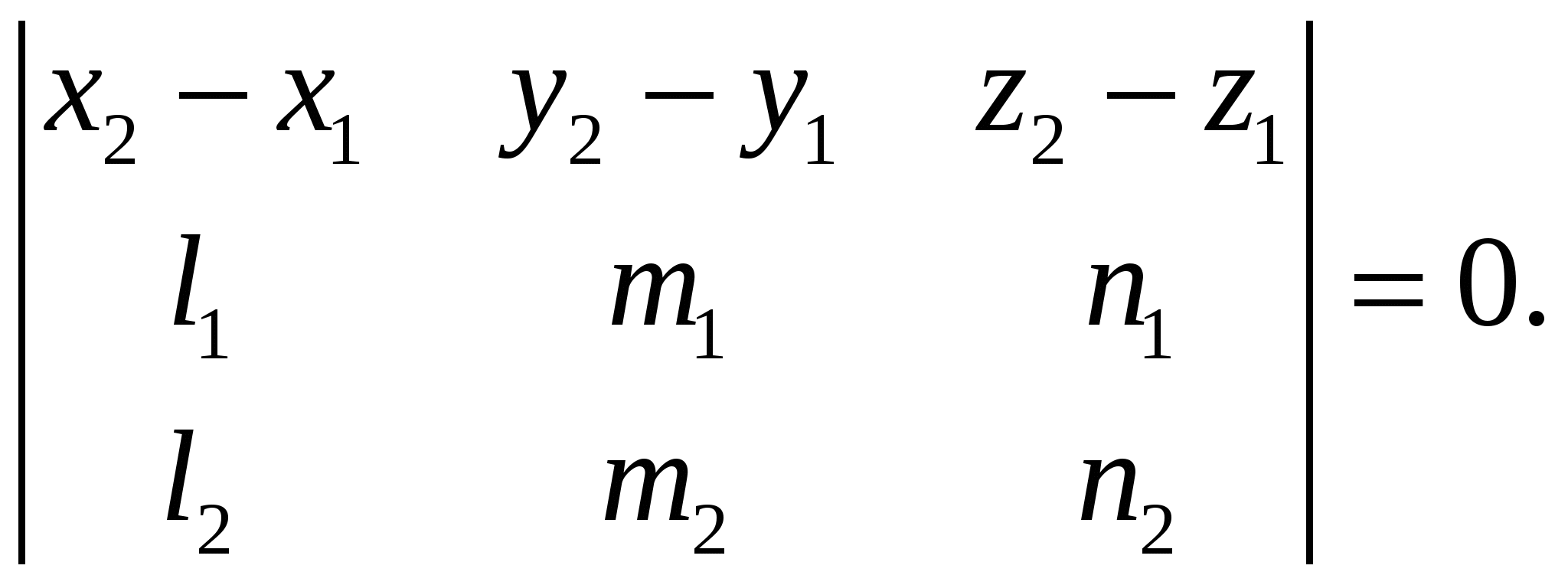
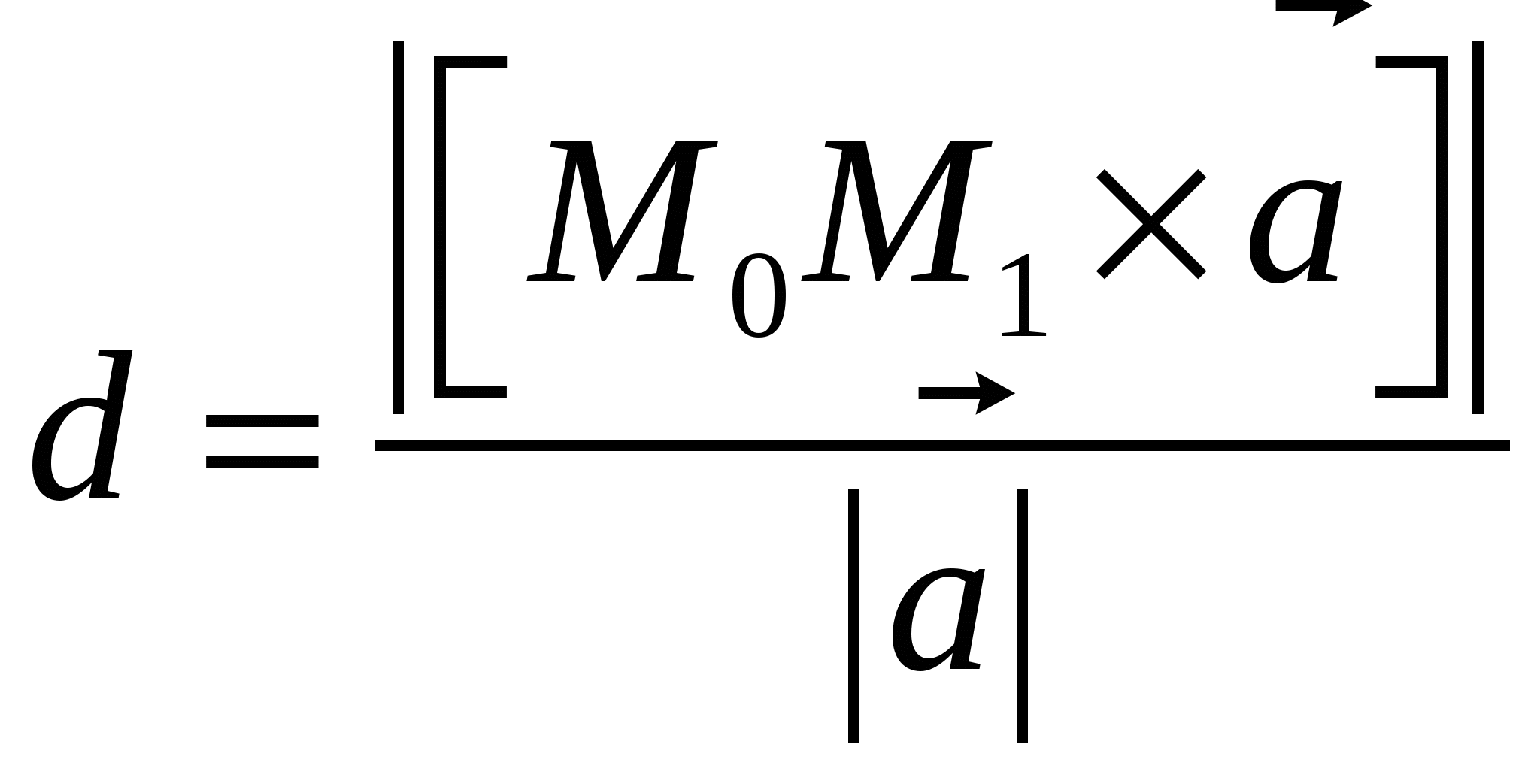 – расстояние от точки – расстояние от точки 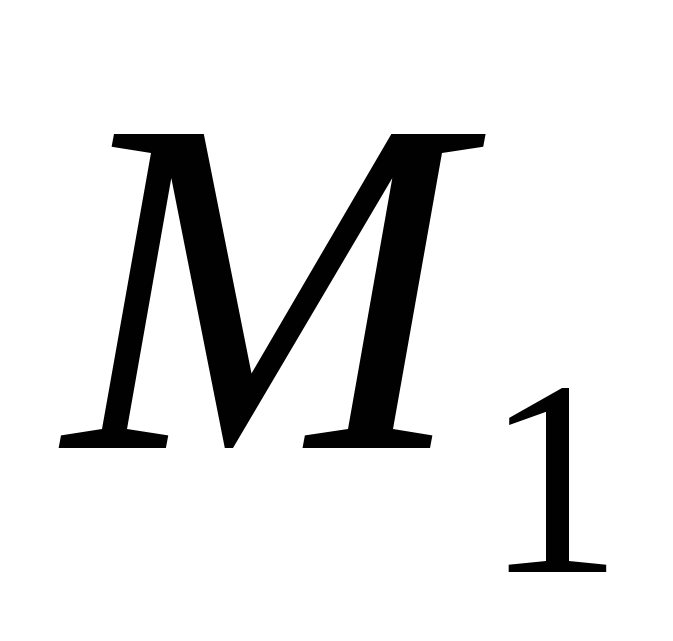 до прямой, проходящей через точку до прямой, проходящей через точку 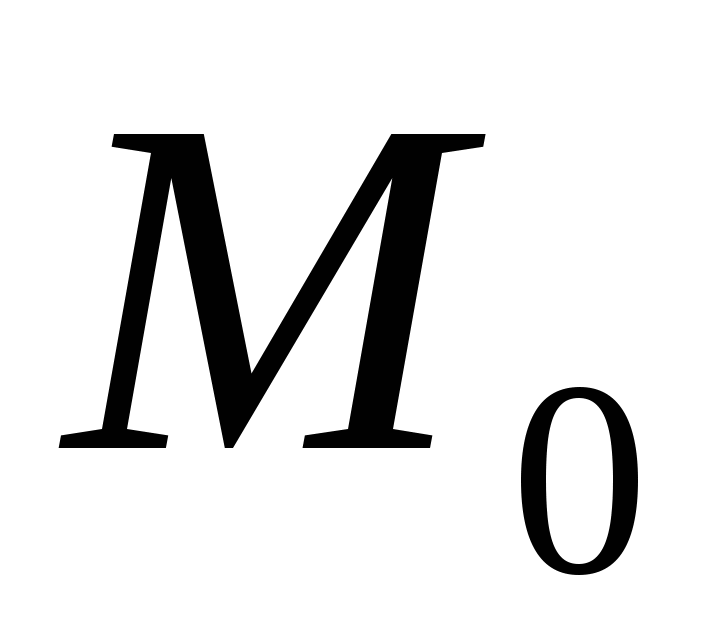 с направляющим вектором с направляющим вектором  ; ;
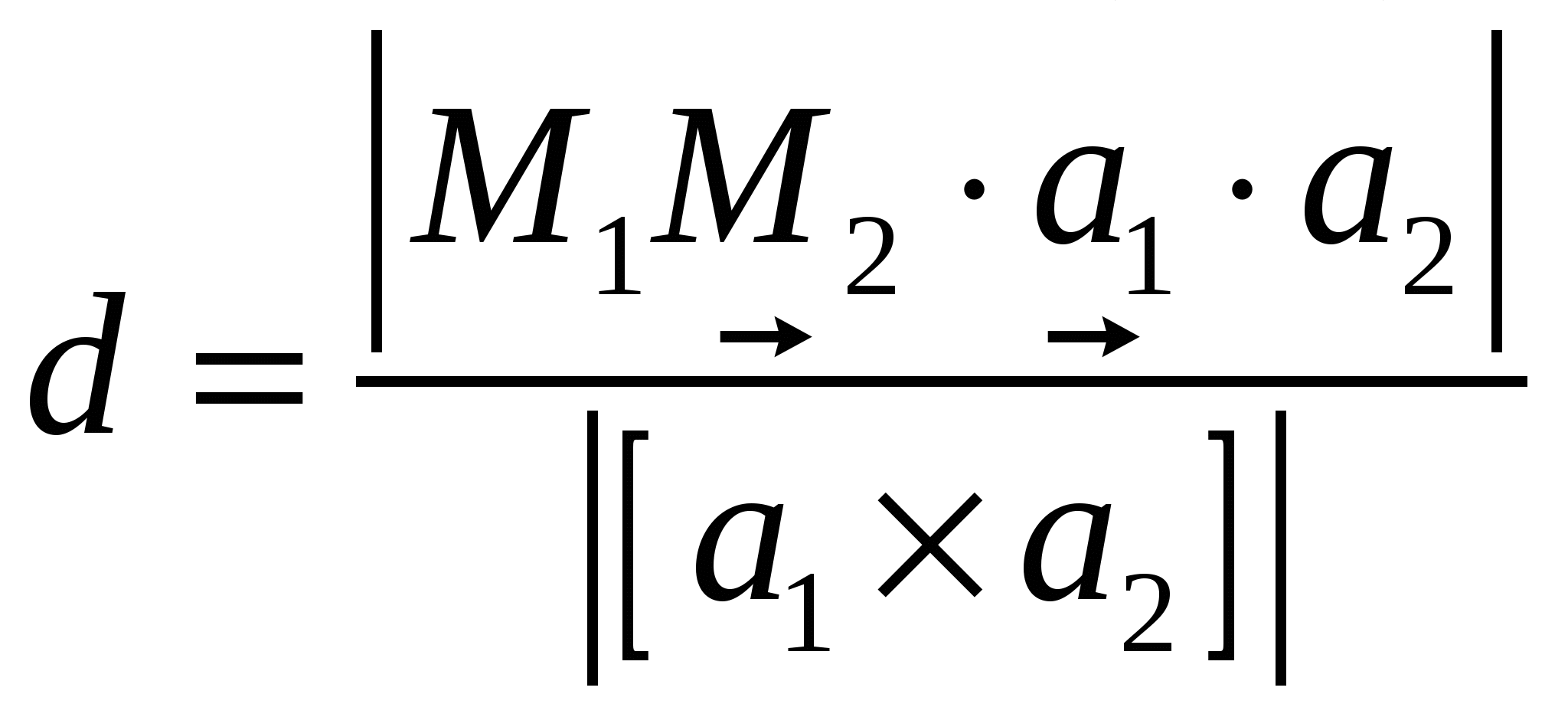 – расстояние между скрещивающимися прямыми: – расстояние между скрещивающимися прямыми: 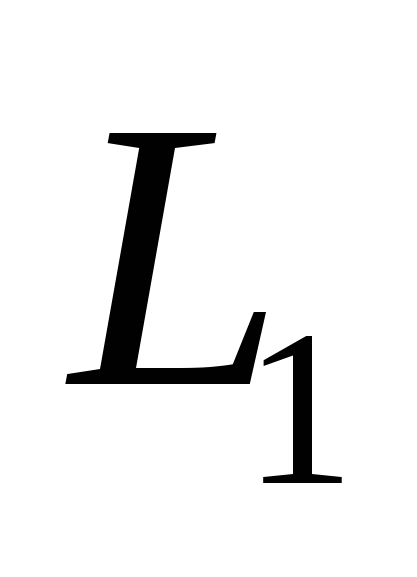 , проходящей через точку , проходящей через точку 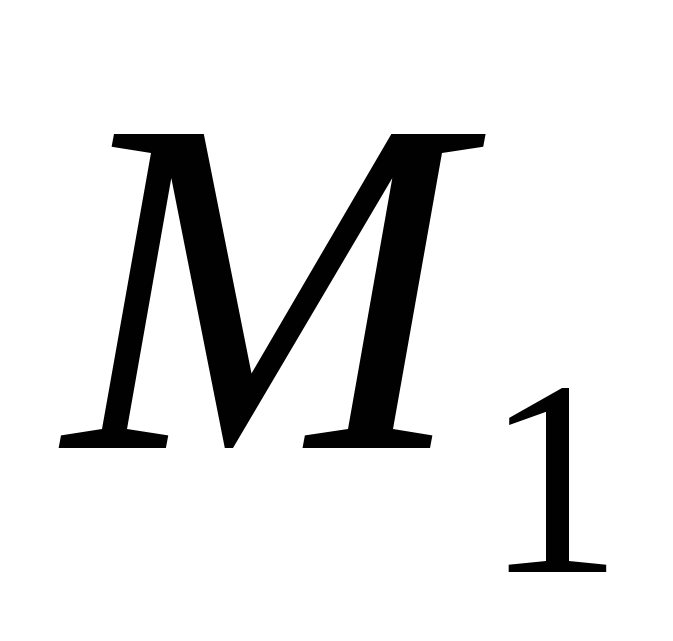 с направляющим вектором с направляющим вектором 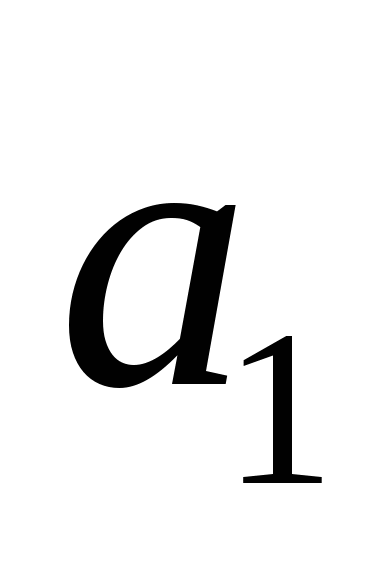 , и , и 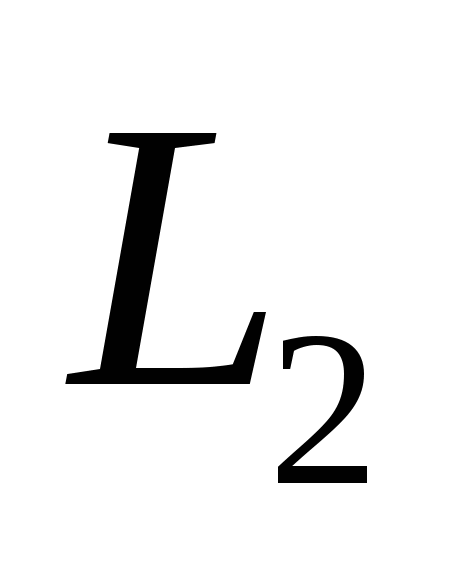 с направляющим вектором с направляющим вектором 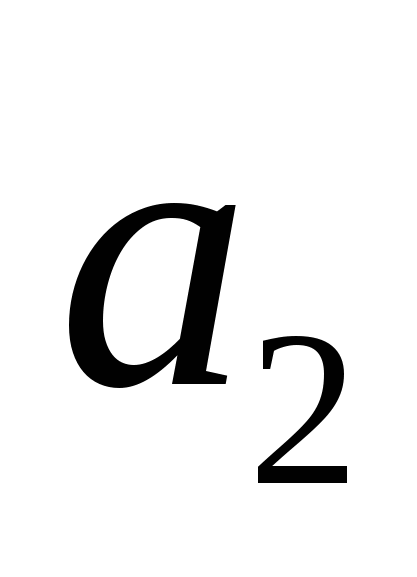 , проходящей через точку , проходящей через точку 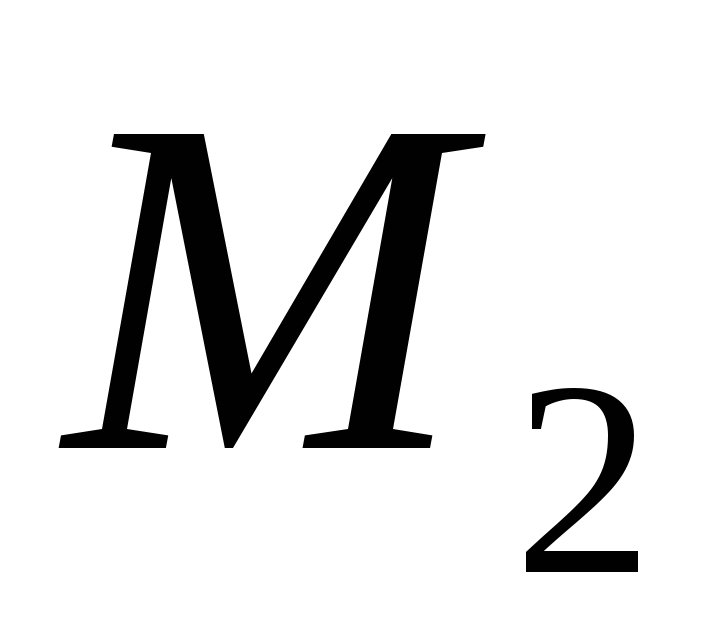 ; ;
|
 Скачать 1.58 Mb.
Скачать 1.58 Mb.