|
|
механика. Билет 7 Законы трения
Билет №7
1. Законы трения:
1. Сила трения скольжения направлена противоположно возможному движению тела.
2. Сила трения не зависит от площади соприкасающихся поверхностей.
3. Максимальная сила трения пропорциональна нормальному
давлению. Под нормальным давлением понимают полное давление на всю площадь соприкосновения трущихся поверхностей:
 . .
4.Коэффициент трения скольжения зависит от материала и
физического состояния трущихся поверхностей.
2. Скорость распространения упругих возмущений.
Если в каком-либо месте упругой среды возникла деформация, то по прекращении внешних воздействий она не остается на месте, а распространяется в среде во всех направлениях. В таких случаях говорят о распространении в среде упругих возмущений или волн. Примерами могут служить звуковые волны в твердых телах, жидкостях или газах.
Пуст имеется прямолинейный ряд, состоящий из одинаковых твердых идеально упругих шаров, соприкасающихся между собой. Ряд таких шаров неограничен. Нанеся удар по первому шару, сообщим ему некоторую скорость V. Первый шар ударится о второй. При упругом ударе шары просто обмениваются скоростями: первый шар остановится, а второй придет в движение с той же скоростью V. Затем второй шар передаст движение третьему, а сам остановится. Движение будет передаваться от шара к шару. В результате возникает возмущение, распространяющееся вдоль ряда шаров. Скорость распространения такого возмущения можно обозначить как с. Ее нельзя смешивать со скоростью V того шара, который в рассматриваемый момент движется.
Формула:  , где с-скорость распространения упругих возмущений, ρ –плотность тела, Е – энергия. , где с-скорость распространения упругих возмущений, ρ –плотность тела, Е – энергия.
|
Билет №19.
1. Теорема Гюйгенса-Штейнера.
Момент инерции тела относительно какой-либо оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями. 
2. Затухающие колебания.
Затухающими колебаниями называют колебания, энергия которых уменьшается со временем. Амплитуда затухающих колебаний уменьшается со временем в зависимости от коэффициента затухания 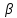 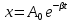 . Затухающие колебания являются непериодическими, т.к. в них никогда не повторяются значения физических величин. Условным периодом колебаний называется промежуток времени, через который физические величины принимают аналогичные значения. . Затухающие колебания являются непериодическими, т.к. в них никогда не повторяются значения физических величин. Условным периодом колебаний называется промежуток времени, через который физические величины принимают аналогичные значения.  Циклическая частота затухающих колебаний показывает, сколько раз за n секунд маятник проходит положение равновесия. Циклическая частота затухающих колебаний показывает, сколько раз за n секунд маятник проходит положение равновесия. 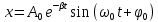 A-амплитуда, A-амплитуда, 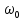 - круговая частота собственных колебаний, - круговая частота собственных колебаний, 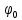 - начальная фаза, - начальная фаза,  - фаза колебаний - фаза колебаний
|
Билет № 21
1. Кинематика материальной точки. Угловые характеристики движения.
В кинематике рассматривается механическое движение без выяснения причин, его вызывающих. Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени. При изучения механического движения реальных объектов в физике используются физические модели, такие как материальная точка, система материальных точек, абсолютно твердое тело, сплошная среда. Материальная точка – тело, размерами и формой которого можно пренебречь в условиях данной задачи. Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстояниями от него до других тел. Траектория – линия, вдоль которой материальная точка движется в пространстве в выбранной системе отсчета. По форме траектории движение можно разделить на прямолинейное и криволинейное. Для характеристики положения материальной точки используют радиус-вектор. Расстояние S, отсчитанное по траектории называется длиной пути AB=S. Вектор, соединяющий начальную и конечную точки траектории называется перемещением. Движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением. Для описания поступательного движения достаточно выбрать одну точку и описать ее движение. Движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой, называется вращательным движением. Абсолютно твердое тело – тело, размеры и форма которого не меняются в процессе движения. Чтобы описать механическое движение тела, нужно знать его координаты в любой момент времени. Для определения координат материальной точки следует выбрать тело отсчета и связать с ним систему координат. Система координат, тело отсчета, с которым она связана, и указание начала отсчета времени образуют систему отсчета, относительно которой рассматривается движение тела. Для описания многих движений систему отсчета связывают с Землей, считая ее неподвижной. В ряде случаев в качестве тела отсчета выбирают Солнце или отдаленные звезды. Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно. Основными кинематическими характеристиками движения материальной точки являются скорость и ускорение.
угловые характеристики движения:
Угловая скорость – это вектор, направление которого совпадает с осью вращения и определяется по правилу правого винта
Средняя угловая скорость – это есть отношение угла поворота ко времени, за которое этот поворот произошел.
Мгновенная угловая скорость – это предел, к которому стремится средняя угловая скорость при ∆t → 0
Угловое перемещение (угол поворота) - это угол, на который переместился радиус-вектор при перемещении тела из точки 1 в точку 2.
Угловая скорость — векторная величина, характеризующая быстроту и направление вращения материальной точки или абсолютно твёрдого тела относительно центра вращения.
2. Принцип относительности в релятивистской механике. Преобразование Лоренца.
В релятивистской механике изобретать различные теории для объяснения отрицательных результатов не стоит, ведь это не поможет обнаружить различие между действующими инерциальными системами. Законом природы в этой области науки выступает полное равноправие всех концепций отсчета в отношении электромагнитных и механических явлений. Нет никакого существенного различия между состоянием покоя и прямолинейного равномерного движения. Но теория относительности в релятивистской механике базируется не только на этом принципе, ведь существует еще и второй постулат: скорость света в пустоте одинакова для существующих в той же среде инерциальных систем отсчета. Она не зависит ни от скорости светового сигнала, ни от скорости самого источника. Основные следствия, которые вытекают из постулатов теории относительности, заключаются в следующем: Относительность расстояний между действующими объектами; Относительность промежутков времени; Замедления времени в движущихся системах отсчета. Преобразования Лоренца количественно выражают тот факт, что о времени и о пространстве (координатах) нельзя говорить как о независимых друг от друга понятиях
В науке работает принцип соответствия. Согласно этому принципу всякая новая теория должна включать в себя старую для тех условий, при которых она справедлива. Поэтому преобразования Лоренца при переходе к условиям, в которых верны преобразования Галилея (U << с), должны превращаться в них. Из преобразований Лоренца видно, что при U << с → β << 1, следовательно х = х' + ut; у = у' ; z = z'; t = t' С точки зрения Эйнштейна пространство и время неразрывно связаны друг с другом и равноправны, образуя четырехмерное пространство -время.
Инвариант, то есть является постоянным в любой инерциальной системе отсчета .
Инварианты – это величины, числовые значения которых не изменяются при преобразованиях координат. Инварианты представляют то существенное в объектах, что не зависит от случайного выбора системы координат, а действительно характеризует свойства объекта.

|
Билет №22.
1. Преобразования Галилея.
Преобразования Галилея устанавливают связь между координатами, скоростями и ускорениями м.т. при переходе из одной инерциальной системы отсчета (ИСО) в другую ИСО. Пусть даны две ИСО - одна неподвижная K и другая подвижная K'. Подвижная ИСО K' движется с постоянной скоростью v0 относительно неподвижной K (рис. 1). В классической механике принято, что время во всех системах отсчета течет одинаково, т.е. t' = t. В системе K пространственное положение, скорость и ускорение м.т. Р характеризуется радиус-вектором  , и векторами скорости , и векторами скорости  и ускорения и ускорения 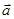 , а в системе K' – векторами , а в системе K' – векторами  ', ',  ' и ' и 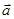 '. Для удобства предположим, что в начальный момент времени (t = 0) начала систем K' и K совпадают. Следовательно, '. Для удобства предположим, что в начальный момент времени (t = 0) начала систем K' и K совпадают. Следовательно,  '(0) = '(0) =  (0). Нашей задачей является найти связь величин (0). Нашей задачей является найти связь величин 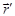 и и  , ,  ' и ' и  , , 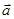 ' и ' и 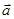 для произвольного момента времени. для произвольного момента времени.
 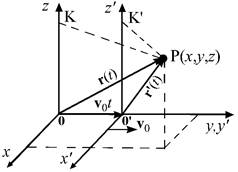
По истечении времени t начало системы координат K' сместится на величину 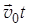 и связь между радиус-векторами точки Р выразится в виде: и связь между радиус-векторами точки Р выразится в виде:
 (t) = (t) =  ' (t) + ' (t) +  0t 0t
или в координатном представлении:
x (t) = x' (t) + v0xt, y (t) = y' (t) + v0yt, z (t) = z' (t) + v0zt.
Найдем связь между скоростями:
 . .
Продифференцируем выражение  = =  ' + ' +  0 по времени. 0 по времени.
Так как скорость подвижной системы отсчета постоянна по отношению к неподвижной системе координат, т.е. , v0 = const, то ускорение м.т. при переходе наблюдателя в подвижную систему отсчета будет таким же, как и в неподвижной системе отсчета: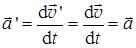 . .
Умножая равенство а' = а на массу m, получим: mа' = mа. Отсюда согласно второго закона Ньютона, записанного в виде m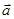 ' = F' и m ' = F' и m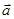 = F, следует, что сила, действующая на м.т. в подвижной и неподвижной ИСО одинакова: F' = F. = F, следует, что сила, действующая на м.т. в подвижной и неподвижной ИСО одинакова: F' = F.
Отсюда следует вывод: законы динамики не изменяются при переходе из одной ИСО в другую ИСО, они – инвариантны (неизменны) относительно преобразования ИСО. Этот результат можно сформулировать в виде механического принципа относительности Галилея: равномерное и прямолинейное движение инерциальной системы отсчета не влияет на ход механических процессов, происходящих в этой системе отсчета т.е. все ИСО эквивалентны по отношению к законам Ньютона. Таким образом, в рамках классической механики невозможно выделить некоторую "главную" ИСО, по отношению к которой состояния покоя и движения тел могли бы считаться абсолютными. Другими словами, никакими механическими опытами невозможно установить, находясь в данной ИСО, движется она или покоится.
2. Уравнение гармонической волны (плоской и сферической).
Уравнение плоской волны
Колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости , т.е.

– это уравнение плоской волны.
Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания A=const. Это будет, если энергия волны не поглощается средой.
Такой же вид уравнение будет иметь, если колебания распространяются вдоль оси y или z.
В общем виде уравнение плоской волны записывается так:
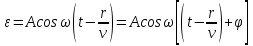
Эти выражения есть уравнения бегущей волны.
Уравнение описывает волну, распространяющуюся в сторону увеличения x.
Так как λ=vT , то 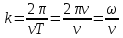 . Отсюда . Отсюда 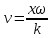 . Тогда уравнение плоской волны запишется так: . Тогда уравнение плоской волны запишется так:
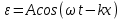
Уравнение сферической волны
В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической.
Предположим, что фаза колебаний источника равна wt (т.е. 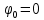 ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу 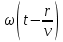 . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону . Следовательно, уравнение сферической волны: . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону . Следовательно, уравнение сферической волны: 
где А равна амплитуде на расстоянии от источника равном единице.
 Уравнение неприменимо для малых r, т.к. при r 0, амплитуда стремится к бесконечности. То, что амплитуда колебаний Уравнение неприменимо для малых r, т.к. при r 0, амплитуда стремится к бесконечности. То, что амплитуда колебаний 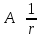 , следует из рассмотрения энергии, переносимой волной. , следует из рассмотрения энергии, переносимой волной.
| |
|
|
 Скачать 1.1 Mb.
Скачать 1.1 Mb.