Декартовы координаты на плоскости. Расстояние между двумя точками.
Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Декартовая (прямоугольная) система координат задается двумя взаимно перпендикулярными прямыми – осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу масштаба обычно берут одинаковой для обеих осей. Эти оси называют осями координат, точку их пересечения О – началом координат. Одну из осей называют осью абсцисс (Ох), другую осью ординат (Оу). Оси координат делят плоскость на четыре области – четверти или квадранты. Систему координат обозначают Оху, а плоскость, в которой расположена система координат, называют координатной плоскостью.
Расстояние между двумя точками A(х1;у1) и B(х2;у2) в прямоугольной системе координат выражается формулой
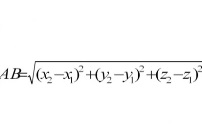
|
Координаты вектора. Скалярное произведение векторов. Угол между векторами.
Координаты вектора равны разностям соответствующих координат его конца и начала: вектор АВ =(х2-х1;у2-у1;z2-z1)
Скалярным произведением двух нулевых векторов a и b называется число, равное произведению длин этих векторов на косинус угла между ними.
a· b = |a|· |b|· cos α
Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
Формула вычисления угла между векторами
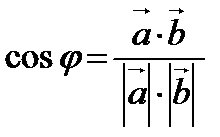
|
Прямая линия в пространстве.
Векторное уравнение прямой
r = r0 + tS
Параметрические уравнения прямой
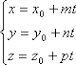
Канонические уравнения прямой
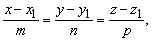
Уравнение прямой в пространстве, проходящей через две данные точки
Уравнения прямой, проходящей через две точки A (x1, y1, z1) и B (x2, y2, z2) имеют вид
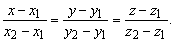
Общее уравнения прямой
Прямая линия в пространстве определена как пересечение двух непараллельных плоскостей, поэтому мы можем рассмотреть систему уравнений
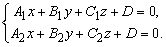
Каждое из уравнений этой системы определяет плоскость. Если плоскости не параллельны, то система определяет прямую L как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы. От общих уравнений можно перейти к каноническим.
|
Координаты точек, делящей отрезок в заданном соотношении.
Если известны две точки плоскости А(ха,уа) и В(хв,ни) то координаты точки М, делящий отрезок в заданном соотношении L=AM/ВМ выражается формулами
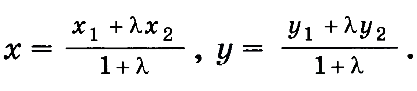
|
Уравнение прямой с угловым коэффициентом. Угол между прямыми. Условия параллельности и перпендикулярности.
Если в обще уравнении прямой В неравно 0, то его можно записать в виде уравнения с угловым коэффициентом y=Kx+b, где K=-A/B=tgL (угл. Коэф), a – угол образованный прямой с + направлением, b = -C/B свободный член = ординате точки пересечения с осью оу
Угол между двумя прямыми равен углу между их направляющими векторами. координаты направляющих векторов a = (x1; y1; z1) и b = (x2; y2; z2), то косинус угла по формуле:
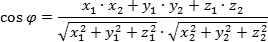
Пусть на плоскости заданы две прямые:
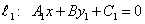
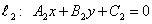
Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны, т.е.
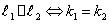
Две прямые перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, т.е.
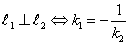
|
Кривые второго порядка. Эллипс.
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Каноническое уравнение Эллипса:
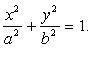
|
Общее уравнение прямой на плоскости. Геометрический смысл коэффициентов.
прямая на плоскости может быть задана уравнением первого порядкаАх + Ву + С = 0. Где А, B, C — произвольные числа, причем А и В не равны нулю одновременно. Это уравнение называют общим уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:• если А = 0, то прямая параллельна оси Ох;• если B = 0, то прямая параллельная оси Оу;• если С = 0, то прямая проходит через начало координат. Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
Геометрический смысл коэффициентов заключается в том, что в декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой, заданной уравнением Ах + Ву + С = 0. Коэффициенты А и В являются координатами нормального вектора, а С = -Ах – Ву —свободный член.
|
Уравнение прямой, проходящей через две заданные точки.
На плоскости даны две точки 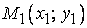 и и 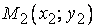 . Уравнение прямой, проходящей через эти точки, очень легко написать. На прямой возьмем любую точку . Уравнение прямой, проходящей через эти точки, очень легко написать. На прямой возьмем любую точку 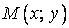 . .
Построим два вектора 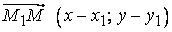 и и 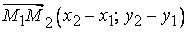 По построению эти векторы коллинеарны. Условие коллинерности – это пропорциональность одноименных координат векторов: По построению эти векторы коллинеарны. Условие коллинерности – это пропорциональность одноименных координат векторов: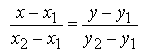 . Это и есть искомое уравнение. . Это и есть искомое уравнение.
|
Кривые второго порядка. Гипербола.
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Каноническое уравнение Гиперболы:
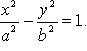
|
Расстояние от точки до прямой.
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую. Формула для вычисления расстояния от точки до прямой на плоскости
Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти, используя следующую формулу:
d =
|
|A·Mx + B·My + C|
|
√A2 + B2
|
|
Плоскость в пространстве.
Всякая плоскость в пространстве определяется линейным уравнением
Ax + By + Cz + D = 0 и обратно, всякое линейное уравнение определяет плоскость в пространстве.
|
Кривые второго порядка. Парабола.
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p>0).
Канонической уравнение Параболы:
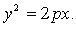
|
Система линейных уравнений с неизвестным. Метод Гаусса.
Это последовательное исключение неизвестных, состоявшее из двух этапов.
1. приведение к треугольному виду
2. идет последовательное определение неизвестных из этой ступенчатой системы
|
Операции над п – мерными векторами. Векторная форма записи системы линейных уравнений.
N-мерным вектором называется последовательность чисел. Эти числа называются координатами вектора. Число координат вектора n называется размерностью вектора.
Вектор записывается в виде строки или столбца:
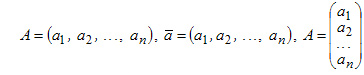
Система уравнений может быть записана в векторном виде:
A1x1 + A2x2 + ... + Anxn =B
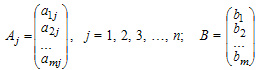
|
Линейная зависимость векторов. Ранг системы векторов. Теорема Кронекера – Капелли о множестве решений системы линейных уравнений.
Векторы a1,а2….аn называются линейнозависимыми, если существуют такие числа λ1, λ2… λn одновременно неравные нулю, такие, что линейная комбинация чисел λ и векторов a равна нулю.
Рангом системы векторов называется максимальное число линейно независимых векторов системы.
Теорема 1 (Кронекера-Капелли)
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы
|
Лемма о решениях однородной системы уравнений. Базис. Разложение вектора по базису.
Лемма. Если в однородной системе уравнений число неизвестных больше, чем число уравнений, то у такой системы бесконечное множество решений.
Базис. Базисом системы векторов A1, A2, ..., An называется такая подсистема B1, B2, ..., Br которая удовлетворяет следующим условиям:
1. B1, B2, ..., Br линейно независимая система векторов;
2. любой вектор Aj системы A1, A2, ..., An линейно выражается через векторы B1, B2, ..., Br
r — число векторов, входящих в базис.
Чтобы разложить, вектор b по базисным векторам a1, ..., an, необходимо найти коэффициенты
x1, ..., xn, при которых линейная комбинация векторов a1, ..., an равна вектору b,
x1a1 + ... + xnan = b,
при этом коэффициенты x1, ..., xn, называются координатами вектора b в базисе a1, ..., an.
|
Определитель квадратной матрицы. Свойства. (Одно доказать)
Матрица размера NxN называется квадратной, где число n называется порядком матрицы.
Свойство 1 («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот. (Строки и столбцы = ряды определителя)
Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
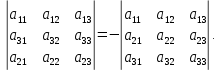
Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.
 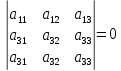
Свойство 4. Общий множитель элементов какого – либо ряда определителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
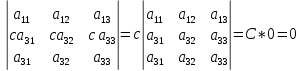
Свойство 5. Если элементы какого – либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
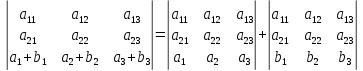
Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ядра прибавить соответствующие элементы параллельного ряда, умноженные на любое число.
Дальнейшие свойства связаны с понятием минора и алгебраического дополнения.
Минором 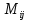 элемента элемента 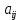 определителя определителя  называется определитель, полученный из называется определитель, полученный из  вычеркиванием вычеркиванием 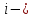 той строки и той строки и 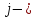 го столбца. го столбца.
Алгебраическим дополнением 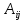 элемента элемента 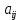 определителя определителя  называется число, равное называется число, равное
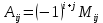 . .
Алгебраическое дополнение либо совпадает с минором элемента, либо отличается от него знаком.
Свойство 7. («Разложения определителя по элементам некоторого ряда»). Определитель равен сумме произведения элементов некоторого ряда на соответствующие им алгебраические дополнения.
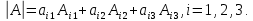
Свойство 8. Сумма произведений элементов какого – либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
a11A21 + a12A22 + a13A23 = 0
|
Алгебраическое дополнение элемента матрицы. Теорема о расположении определителя по столбцу (строке).
Алгебраическим дополнением 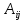 элемента элемента 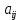 определителя определителя  называется число, равное называется число, равное
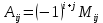 . .
Алгебраическое дополнение либо совпадает с минором элемента, либо отличается от него знаком.
Разложения определителя по элементам некоторого ряда. Определитель равен сумме произведения элементов некоторого ряда на соответствующие им алгебраические дополнения.
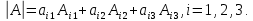
|
Сложение и умножение матриц. Матричная форма записи системы линейных уравнений.
Складывать можно только матрицы одного порядка
при сложении матриц складываются соответствующие эл-ты метриц (а11+а11,а12+а12) и т.д
умножение матриц
Матрицы можно умножать только в том случае, если количество строк матрицы А равно количеству столбцов матрицы В
матричная форма:АХ=В
где А-матрица системы, Х-столбец неизвестных, В-атолбец свободных членов. Решение такого уравнения. Х=А-1 В
|
Теорема Крамера.
Если матрица является невырожденной, т.е. ее определитель не равен нулю, ее можно решить по формулам крамера
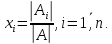
|
Ранг матрицы (теорема о равенстве строчного и столбцового рангов, базисный минор).
Рангом матрицы называется наибольший из порядков ее не равных нулю миноров. Ранг нулевой матрицы по определению равен нулю.
Пусть ранг матрицы 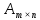 равен равен 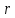 . Любой отличный от нуля минор . Любой отличный от нуля минор 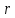 - го порядка называется базисным. Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными. - го порядка называется базисным. Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными.
Теорема 1. (О ранге матрицы). У любой матрицы минорный ранг равен строчному рангу и равен столбцовому рангу.
Теорема 2.(О базисном миноре). Каждый столбец матрицы раскладывается в линейную комбинацию ее базисных столбцов.
|
Отображение векторов, определяемое матрицей. Обратное отображение. Обратная матрица.
Отображение векторов, определяемое матрицей???
Обратное отображение ???
Обратная матрица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
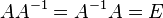
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.
Свойства обратной матрицы:
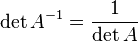 , где , где 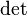 обозначает определитель. обозначает определитель.
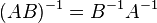 для любых двух обратимых матриц для любых двух обратимых матриц 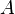 и и 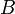 . .
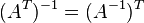 , где , где 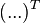 обозначает транспонированную матрицу. обозначает транспонированную матрицу.
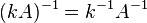 для любого коэффициента для любого коэффициента 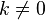 . .
|
Выражение элементов обратной матрицы через определители
Рассмотрим квадратную матрицу. Обратную матрицу можно найти по следующей формуле:
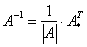 где где 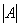 – определитель матрицы – определитель матрицы 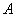 , , 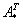 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 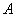 . .
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д. Найти обратную матрицу для матрицы 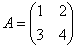 . .
1) Сначала находим определитель матрицы.
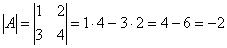
В том случае, если определитель матрицы равен нулю – обратной матрицы не существует.
В рассматриваемом примере, как выяснилось, 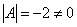 , а значит, всё в порядке. , а значит, всё в порядке.
2) Находим матрицу миноров  . .
Матрица миноров имеет такие же размеры, как и матрица  , то есть в данном случае , то есть в данном случае  . .
Возвращаемся к нашей матрице 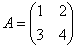
Сначала рассмотрим левый верхний элемент:
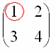
Как найти его минор?
А делается это так: мысленно вычеркиваем строку и столбец, в котором находится данный элемент:
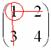
Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров:
Рассматриваем следующий элемент матрицы 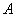 : :
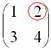
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент:
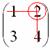
То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу:
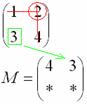
Аналогично рассматриваем элементы второй строки и находим их миноры:
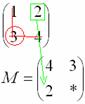
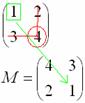
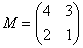 – матрица миноров соответствующих элементов матрицы – матрица миноров соответствующих элементов матрицы 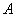 . .
3) Находим матрицу алгебраических дополнений 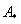 . .
Это просто. В матрице миноров нужно поменять знаки у двух чисел:
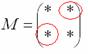
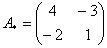 – матрица алгебраических дополнений соответствующих элементов матрицы – матрица алгебраических дополнений соответствующих элементов матрицы 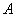 . .
4) Находим транспонированную матрицу алгебраических дополнений 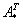 . .
 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 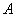 . .
5) Ответ.
Вспоминаем нашу формулу 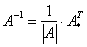
Таким образом, обратная матрица:
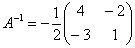
 союзная матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы. Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, ибо понятие алгебраического дополнения вводится для квадратных матриц. союзная матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы. Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, ибо понятие алгебраического дополнения вводится для квадратных матриц.
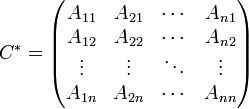
Исходная матрица:
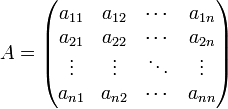
Где:
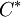 — присоединённая(союзная, взаимная) матрица; — присоединённая(союзная, взаимная) матрица;
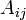 — алгебраические дополнения исходной матрицы; — алгебраические дополнения исходной матрицы;
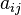 — элементы исходной матрицы. — элементы исходной матрицы.
|
Собственные числа и векторы матриц. Минимальные
и характеристические многочлены матриц.
ненулевой вектор 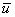 , который при умножении на , который при умножении на
некоторую квадратную матрицу 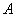 превращается превращается
в самого же себя с числовым коэффициентом 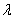 , ,
называется собственным вектором матрицы 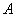 . .
Число 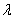 называют собственным значением или называют собственным значением или
собственным числом данной матрицы.
Напомним, что характеристическим многочленом квадратной матрицы 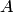 (n-го порядка) называется многочлен (n-го порядка) называется многочлен 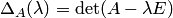 . Степень характеристического многочлена совпадает с порядком матрицы . Степень характеристического многочлена совпадает с порядком матрицы 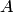 . Рассмотрим другие свойства характеристического многочлена. . Рассмотрим другие свойства характеристического многочлена.
Характеристический многочлен квадратной матрицы 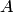 n-го порядка может быть представлен в виде n-го порядка может быть представлен в виде
где 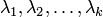 — корни характеристического многочлена (собственные значения матрицы — корни характеристического многочлена (собственные значения матрицы 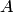 ) кратности ) кратности 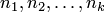 соответственно, причем соответственно, причем 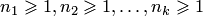 и . и .
|
Симметрическая матрица
квадратная матрица, в которой
любые два элемента, расположенные
симметрично относительно главной диагонали, равны между собой. Симметричная матрица равна транспонированной матрице А=Ат
и она всегда квадратная
|
Квадратичные формы. (Положительный опр-ль, критерий Сильвестра).
квадратичная форма – функция на вектором пространстве задаваемая однородным многочленом второй степени от ординат вектора.
х+х1е1+х2е2….+хnen
Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой. Для того, чтобы квадратичная форма была положительно определена необходимо и достаточно, чтобы определители всех угловых миноров были больше нуля. Следствия критерия Сильвестра
Следствие 1. Для отрицательно определённости квадратичной формы необходимо и достаточно, чтобы знаки угловых миноров чередовались, начиная с минуса.Следствие 2.Невырожденная квадратичная форма является знакопеременной, если и только если выполнено хотя бы одно из следующих условий: Один из угловых миноров равен нулю. Один из угловых миноров четного порядка отрицателен. Два угловых минора нечетного порядка имеют разные знаки. Следствие 3. Если симметрическая матрица положительно определена, то ее диагональные элементы положительны.
|
| |
 Скачать 145.64 Kb.
Скачать 145.64 Kb.