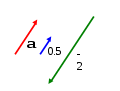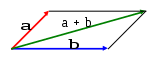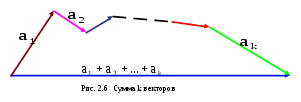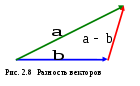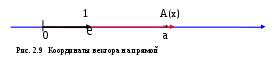Лекции № 3. Векторная алгебра
§2.1. Декартовы системы координат на прямой, плоскости и в пространстве. Расстояние между двумя точками. Деление отрезка в данном отношении
Аналитическая геометрия в отличие от элементарной классической геометрии, изучаемой в школе, даёт возможность решать многие геометрические задачи алгебраическими методами которые не требуют геометрических построений. В её основе лежит понятие системы координат, которое позволяет задавать точки с помощью наборов чисел, а линии и поверхности с помощью уравнений.
Определение. Координатной осью  на прямой называется прямая с выбранным началом координат – точкой на прямой называется прямая с выбранным началом координат – точкой  направлением и масштабным единичным отрезком направлением и масштабным единичным отрезком  . .
При этом каждой точке  на прямой сопоставляется число – её координата x. Соответствующее обозначение на прямой сопоставляется число – её координата x. Соответствующее обозначение 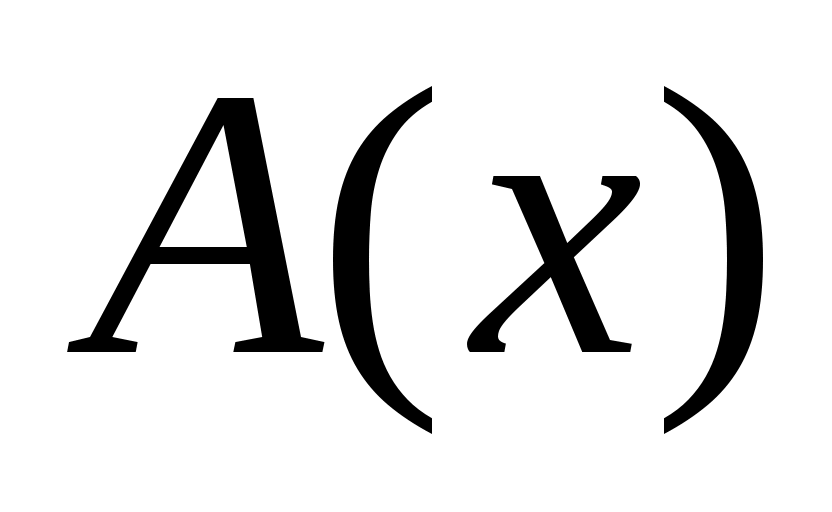 . .

Рис. 2.1 Система координат на прямой
При этом имеется взаимно однозначное соответствие между всеми точками прямой и всеми действительными числами – координатами этих точек.
Определение. Декартовой системой координат (Д.С.К.) на плоскости 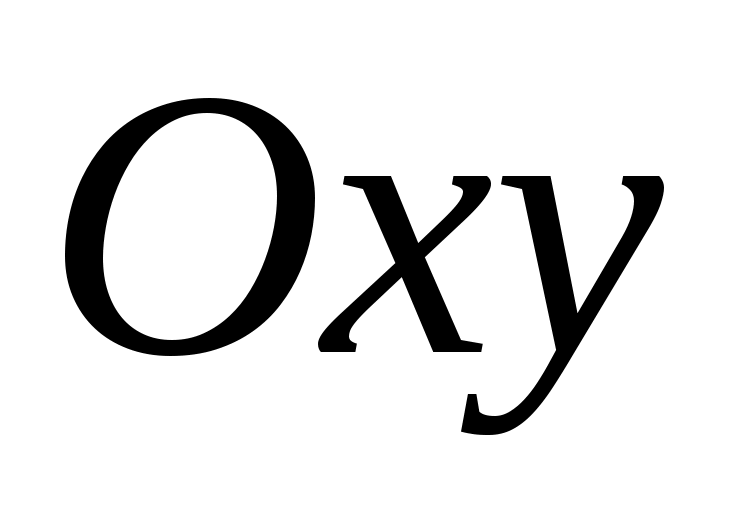 называется пара взаимно перпендикулярных координатных осей на этой плоскости, пересекающиеся в общем начале координат точке называется пара взаимно перпендикулярных координатных осей на этой плоскости, пересекающиеся в общем начале координат точке 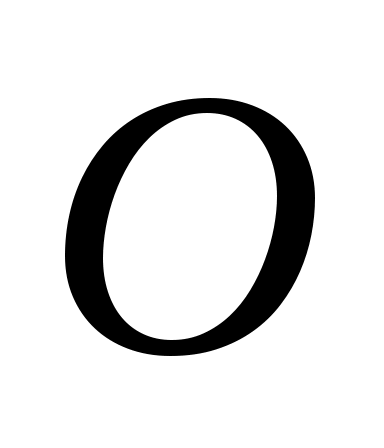 и имеющие равные масштабные отрезки. Первая из этих осей называется осью абсцисс( и имеющие равные масштабные отрезки. Первая из этих осей называется осью абсцисс(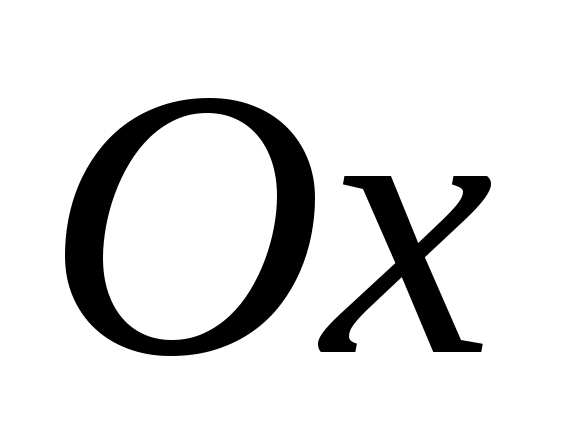 ) а вторая – осью ординат ( ) а вторая – осью ординат ( ). ).
Координаты проекций точки  плоскости на эти оси называются координатами точки плоскости на эти оси называются координатами точки  в Д.С.К. в Д.С.К. 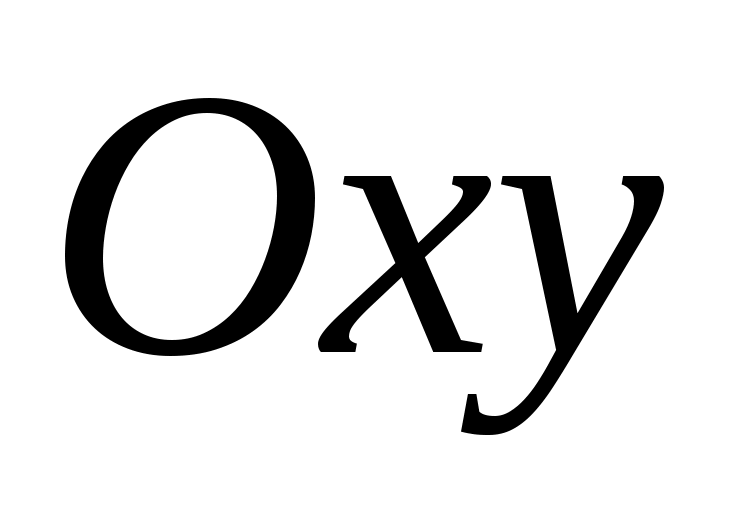 . Это обозначается в виде . Это обозначается в виде 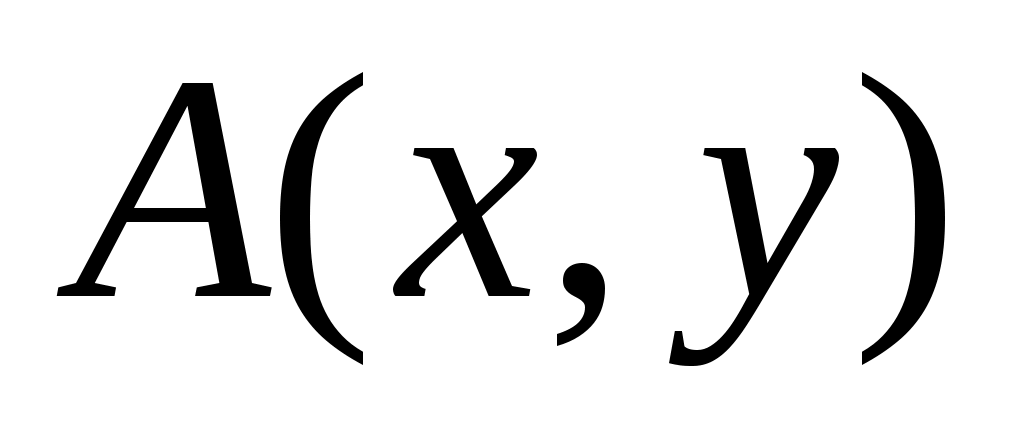 . .
При этом имеется взаимно однозначное соответствие между всеми точками плоскости и всеми парами действительных чисел – координатами этих точек (рис.2.2).
 Рис. 2.2 Система координат на плоскости
Точка O имеет координаты (0,0). Координаты точек на оси Ox имеют вид (x,0). Координаты точек и оси Oy имеют вид (О,у).
Определение.Д.С.К. в пространствеOxyz называется тройка взаимно перпендикулярных осей координат, пересекающихся в общем начале координат точке O и имеющих равные масштабные отрезки.
Третья ось при этом называется осью аппликат (Oz).
Координаты проекции точки A на эти три оси называются координатами точки A в Д.С.К. Oxyz (обозначение A (x,y,z); x– абсцисса, y– ордината, z– аппликата).
При этом имеется взаимно однозначное соответствие между всеми точками пространства и всеми тройками действительных чисел – координатами этих точек.
Точка O имеет координаты O (000). Координаты точек на оси Ox имеют вид (x00), на Oy – (0y0), на Oz –(00z).
§ 2.2. Простейшие задачи аналитической геометрии
Рассмотрим две простейшие задачи: нахождение расстояния между двумя точками и деление отрезка в данном отношении.
Расстояние между точками A и B будем обозначать через AB. Оно обладает следующими свойствами.
AB 0. AB=0 только в том случае, когда A=B. 0. AB=0 только в том случае, когда A=B.
AB=BA.
AC≤AB+BC.
Теорема 1. Расстояние между точками A(xA) и B(xB) на оси Ox находится по формуле AB=xB–xA. Здесь справа записан модуль разности между координатами точек B и A.
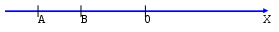
Рис.2.3 Расстояние между точками
Теорема 2. Расстояние между точками A(xA,yA) и B(xB,yB) на плоскости Oxy находится по формуле AB=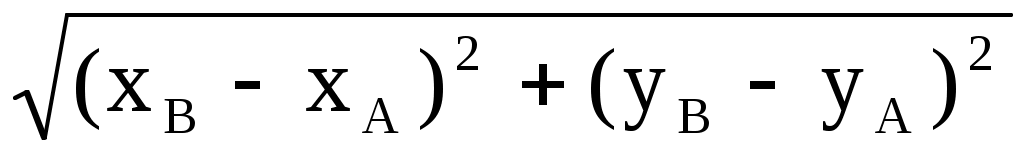 . .
Теорема 3. Расстояние между точками A(xA,yA,zA) и B(xB,yB,zB) в пространстве Oxyz находится по формуле
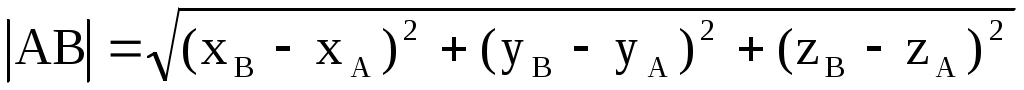 . .
Пример. Пусть A(1,1,1),B(2,3,–1). Найдём |AB|.
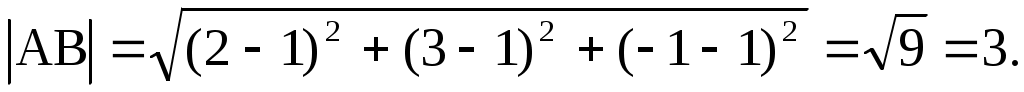
Определение.Разделить отрезокABв отношении   это значит найти на нём такую точку M, что это значит найти на нём такую точку M, что 
Теорема 4. Пусть точки A(xA) и B(xB) лежат на оси Ox и точка M(xM) делит отрезок AB в отношении 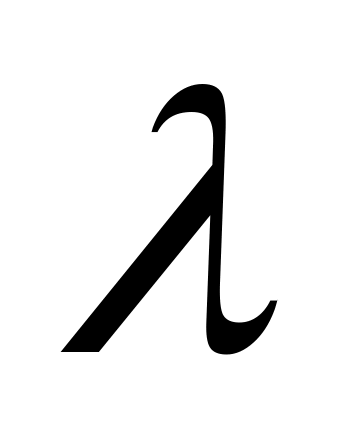 , тогда , тогда 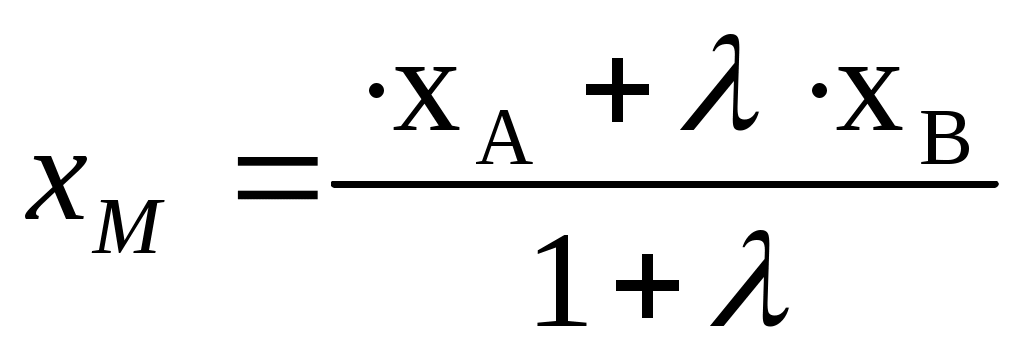 . .
Доказательство. Пусть xBxA, тогда xAxMxB, |AM|=xM–xA, |MB|=xB–xM, из определения точки M получим уравнение:

Решим его. 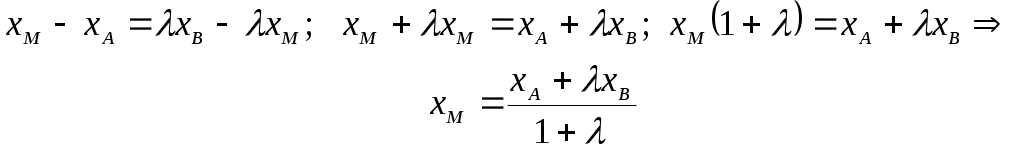
Теорема 5. Пусть точка M(xM,yM,zM) делит отрезок AB в отношении  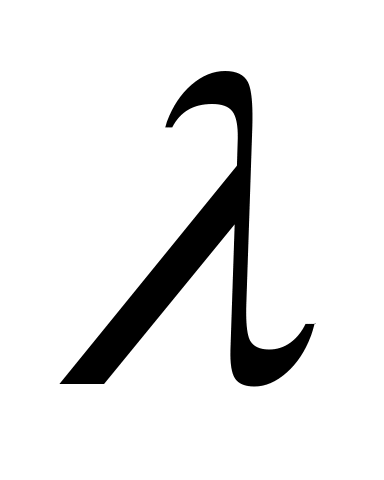 , где A(xA,yA,zA), B(xB,yB,zB), тогда , где A(xA,yA,zA), B(xB,yB,zB), тогда
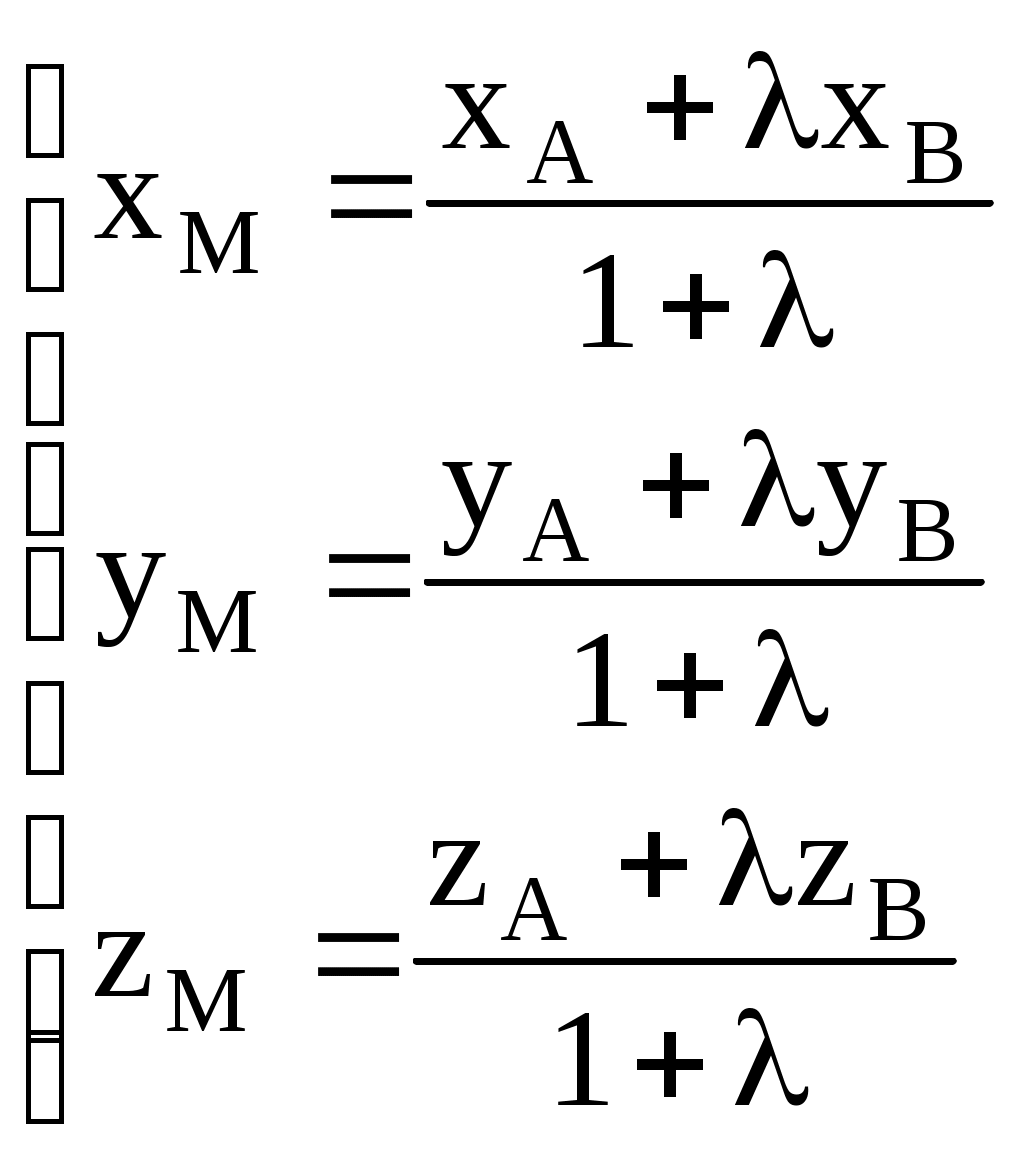
Пример2. Найти координаты точки M,делящей отрезокAB в отношении 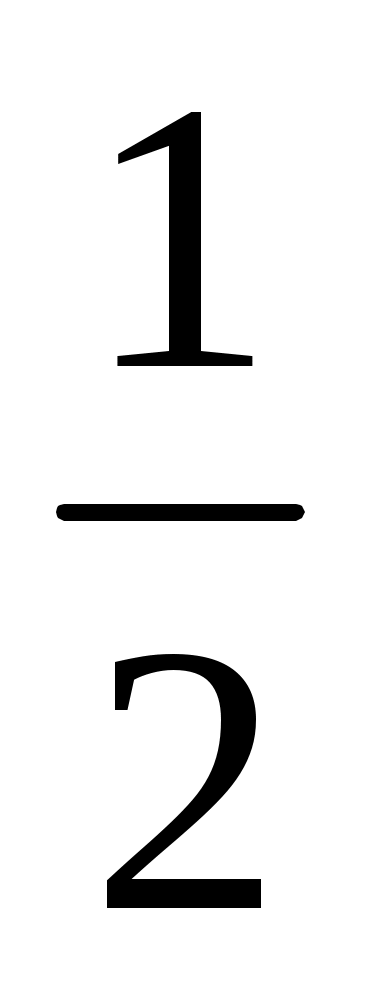 , где A(1,1,2), B(4,7,8). Получим: , где A(1,1,2), B(4,7,8). Получим:
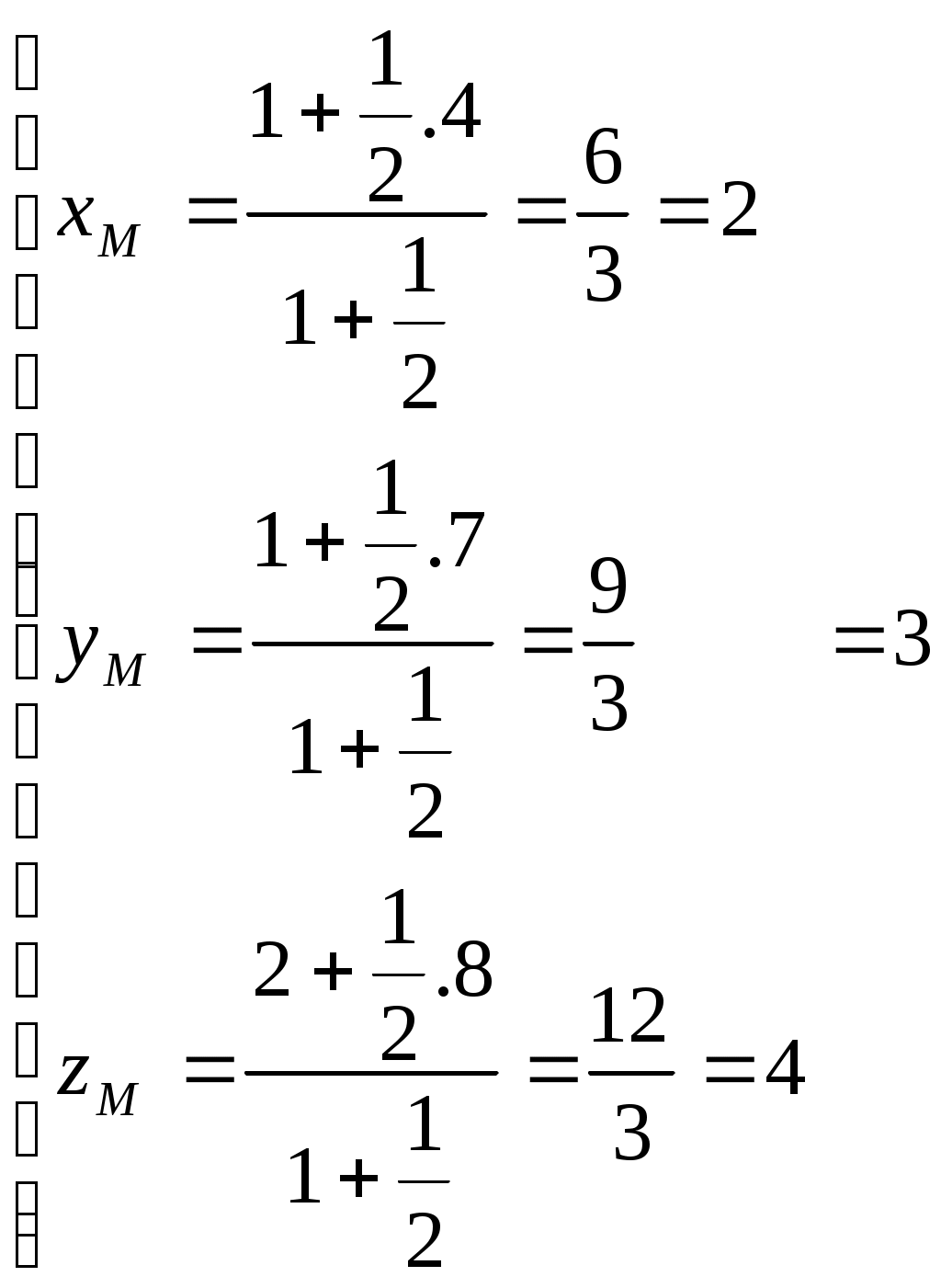 . .
Следовательно,M(2,3,4).
Следствие. Если точка M является серединой отрезка AB, то
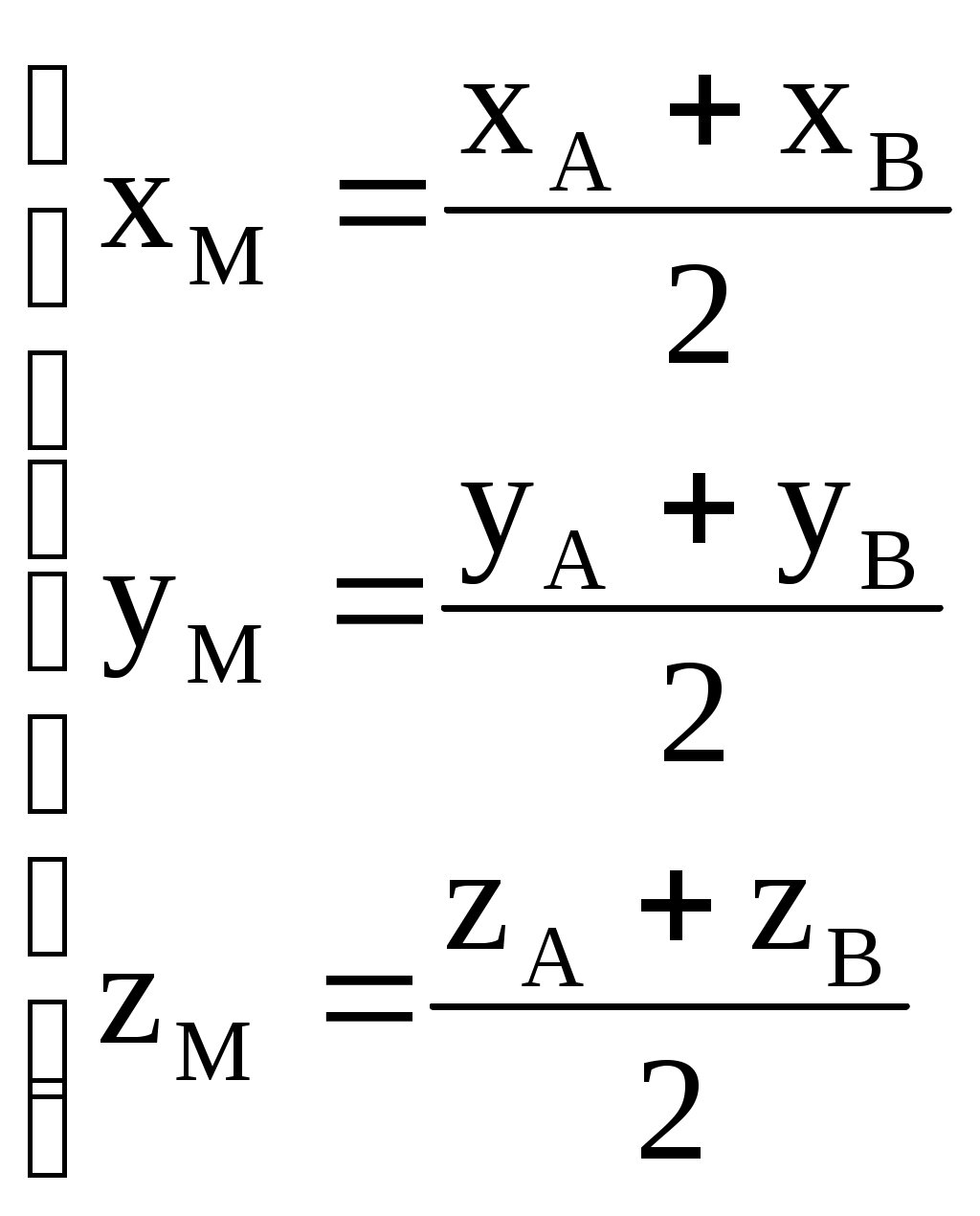 . .
Эти формулы получаются из формул теоремы 5 при ==1.
§ 2.3. Векторы и линейные операции над ними. Базис векторного
пространства. Координаты вектора
Векторы используются для описания величин имеющих определённое направление. Примерами таких величин являются сила, скорость, перемещение.
Определение.Вектором называется отрезок с выбранным направлением, или направленный отрезок.
Вектор с началом в точкеA и с концом в точкеB обозначается через 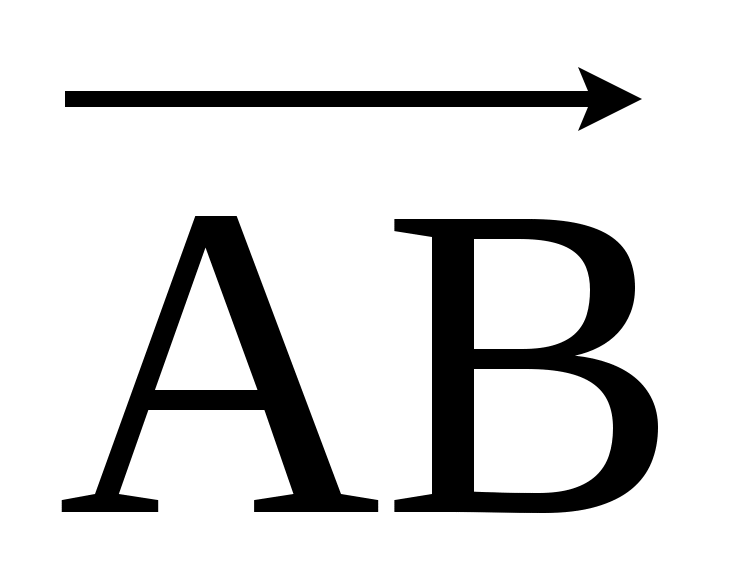 , кроме того вектор можно обозначать одним символом, например , кроме того вектор можно обозначать одним символом, например  . .
Вектор, у которого начало совпадает с его концом называется нулевым вектором и обозначается через  . Длина отрезка, изображающего вектор . Длина отрезка, изображающего вектор  , называется модулем этого вектора и обозначается | , называется модулем этого вектора и обозначается |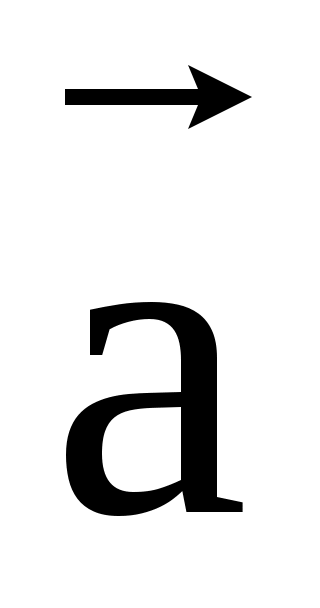 |. |.
Векторы 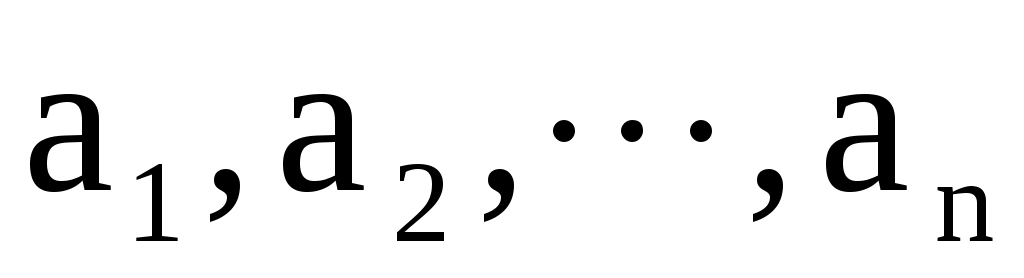 , параллельные одной прямой называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору. , параллельные одной прямой называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору.
Два вектора 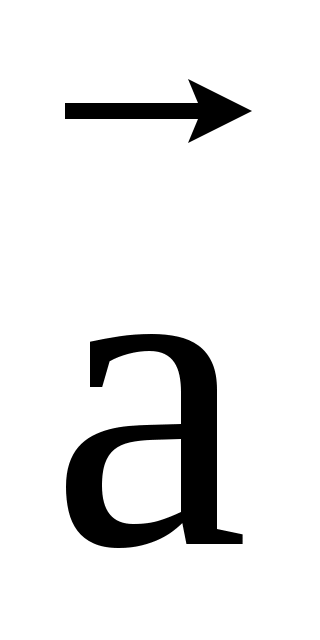 и и  считаются равными, если они равны по модулю, коллинеарны и одинаково направлены. Из этого определения следует, что при параллельном переносе вектор не меняется, по этому в качестве начала вектора можно выбрать любую точку. считаются равными, если они равны по модулю, коллинеарны и одинаково направлены. Из этого определения следует, что при параллельном переносе вектор не меняется, по этому в качестве начала вектора можно выбрать любую точку.
Линейными операциями над векторами называются умножение вектора на число и сложение векторов.
Определение. Произведением вектора  на число называется такой вектор на число называется такой вектор  , что выполняются три условия. , что выполняются три условия.
| |=||| |=||| | |
 || ||
Вектор  сонаправлен вектору сонаправлен вектору  , если 0 и направлен в противоположную сторону, если 0. , если 0 и направлен в противоположную сторону, если 0.
Пример1. Ниже изображены вектора 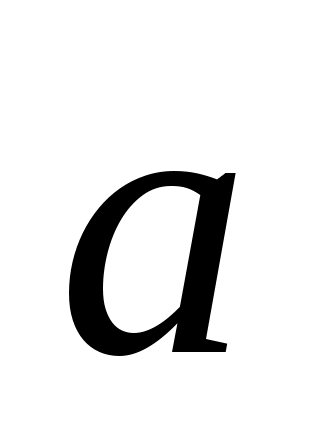 ; 0,5 ; 0,5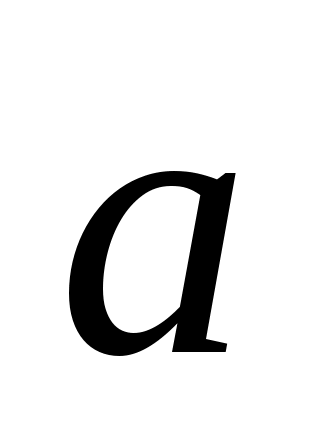 ; –2 ; –2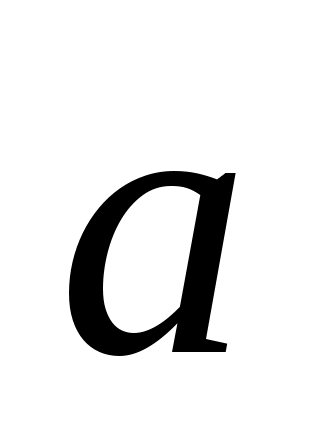 . .
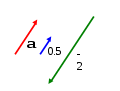
Рис. 2. 4 Умножения вектора на число
Определение. Суммой векторов  и и  исходящих из одной точки называется вектор совпадающий с диагональю параллелограмма, образованного векторами исходящих из одной точки называется вектор совпадающий с диагональю параллелограмма, образованного векторами  и и  исходящий из той же точки. исходящий из той же точки.
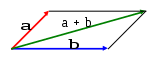
Рис. 2.5 Сложение векторов
Если вектора  и и 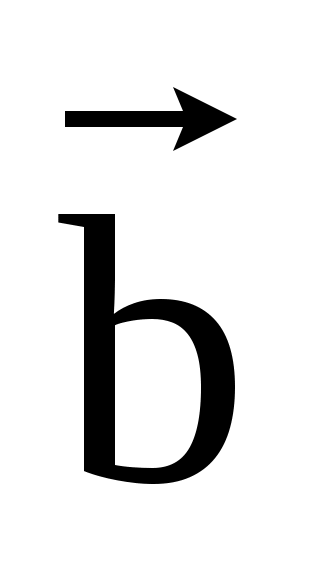 не исходят из одной точки, то их начала необходимо с помощью параллельного переноса перенести в одну точку. Это определение называется правилом параллелограмма. При сложении большого числа векторов удобнее пользоваться следующим определением, равносильным предыдущему. не исходят из одной точки, то их начала необходимо с помощью параллельного переноса перенести в одну точку. Это определение называется правилом параллелограмма. При сложении большого числа векторов удобнее пользоваться следующим определением, равносильным предыдущему.
Суммой векторов 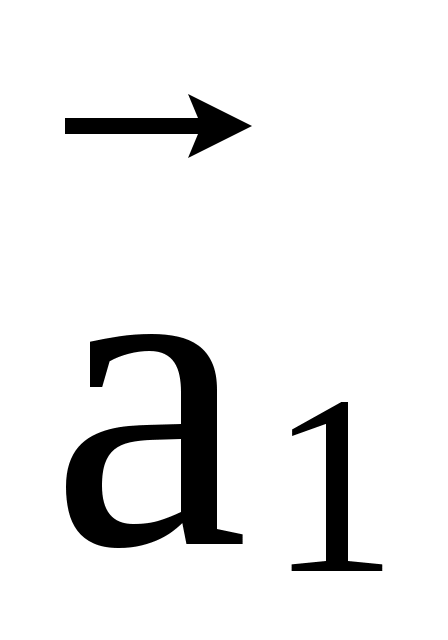 , ,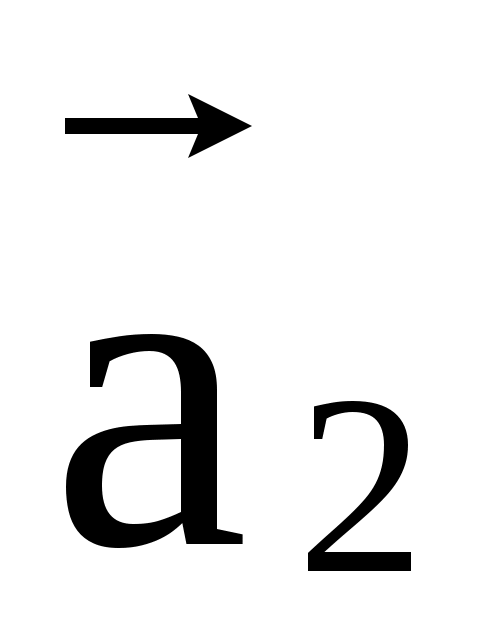 ,..., ,...,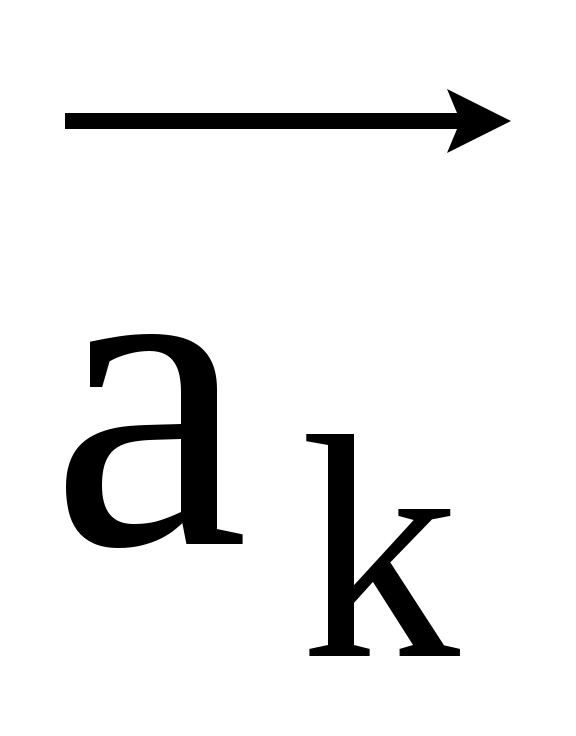 у которых начало у которых начало  вектора совпадает с концом вектора совпадает с концом 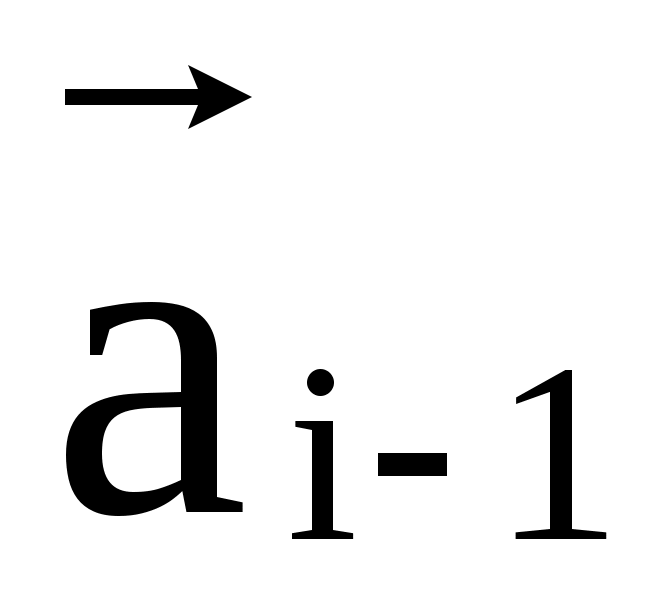 (i=2k), является вектор соединяющий начало вектора (i=2k), является вектор соединяющий начало вектора 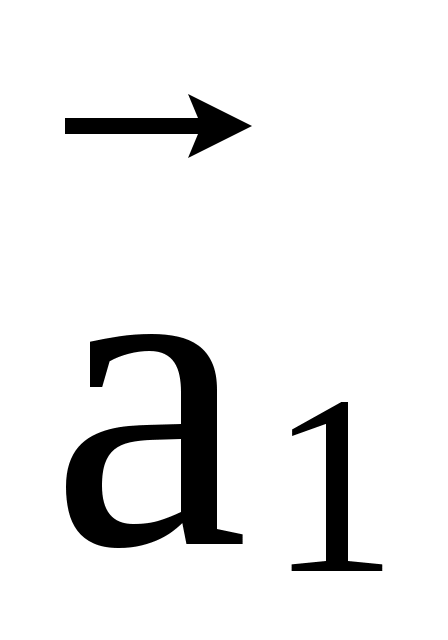 с концом вектора с концом вектора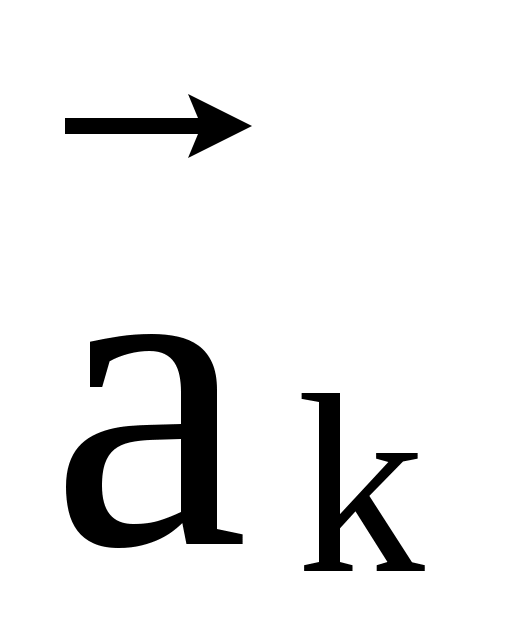 . .
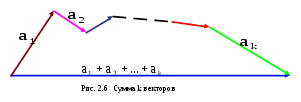
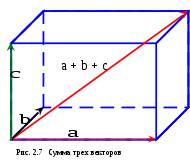
Пример2. Если вектора 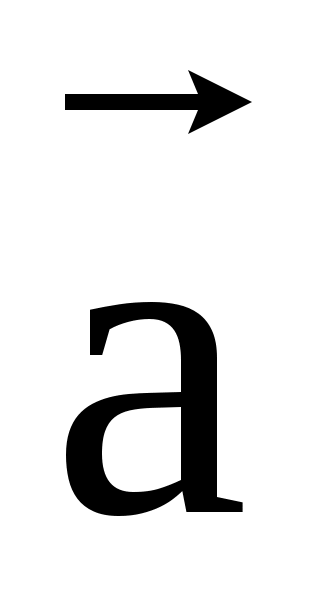 , , 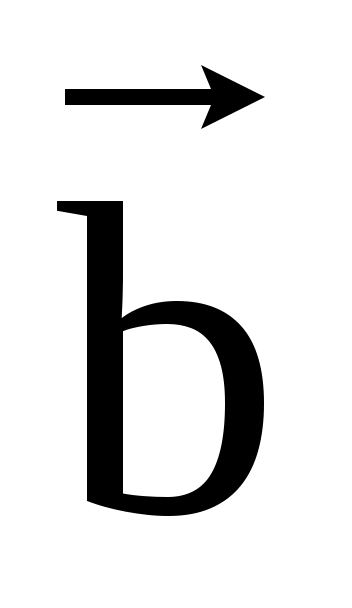 , ,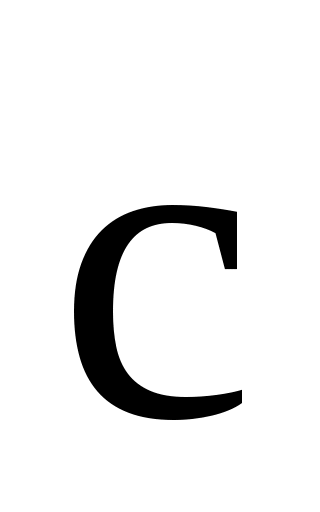 совпадают с тремя рёбрами параллелепипеда исходящими из одной вершины, то их сумма совпадают с тремя рёбрами параллелепипеда исходящими из одной вершины, то их сумма 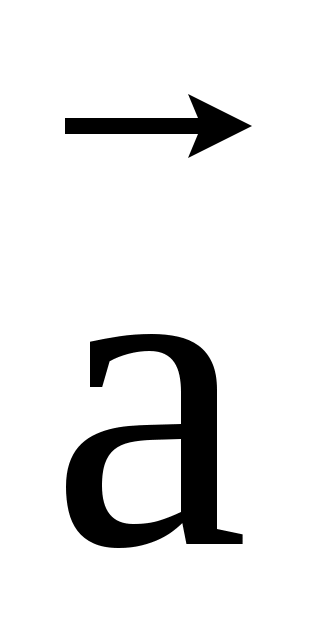 + + + + совпадает с диагональю этого параллелепипеда, исходящей из той же вершины (рис.2.6) совпадает с диагональю этого параллелепипеда, исходящей из той же вершины (рис.2.6)
Эти линейные операции над векторами обладают следующими свойствами.
1 = =
0 = =
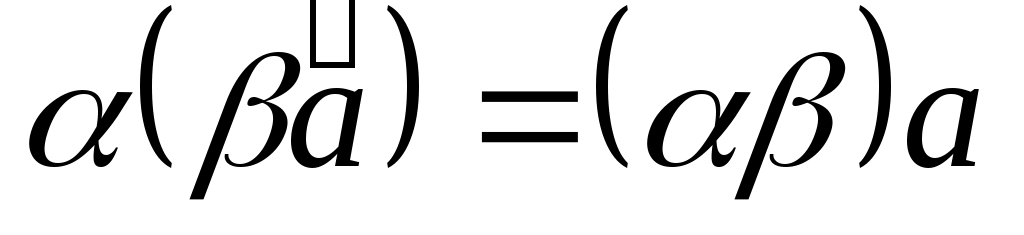


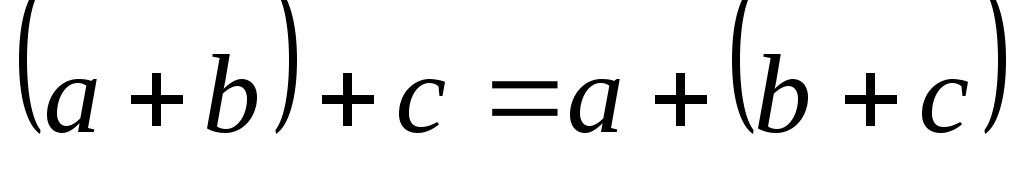
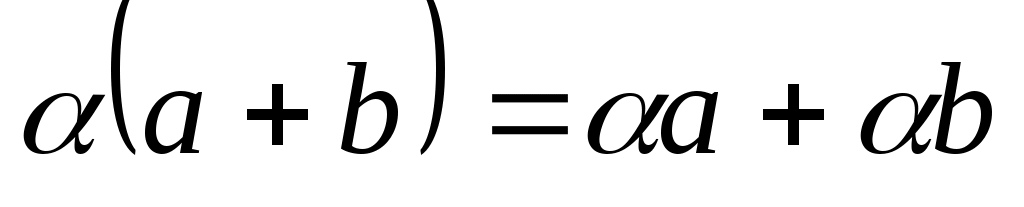
Операция разности векторов  и и  сводится к двум линейным операциям: сводится к двум линейным операциям:  , однако часто удобней пользоваться следующим специальным определением равносильным вышеприведённому. , однако часто удобней пользоваться следующим специальным определением равносильным вышеприведённому.
Определение. Разностью векторов 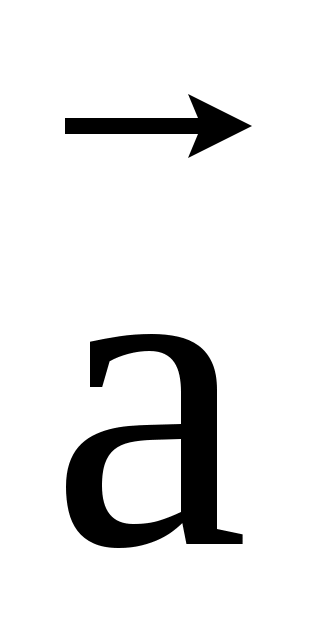 и и  , исходящих из одной точки называется вектор, соединяющий конец вектора , исходящих из одной точки называется вектор, соединяющий конец вектора 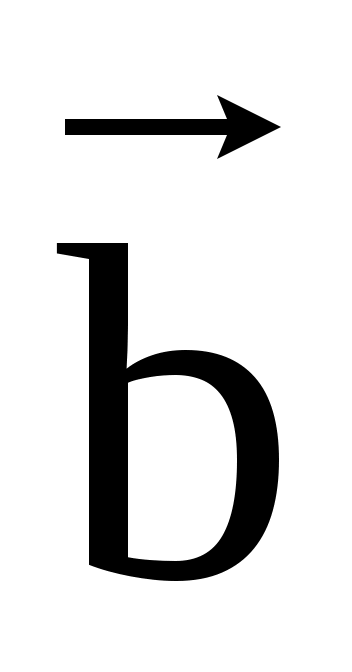 с концом вектора с концом вектора 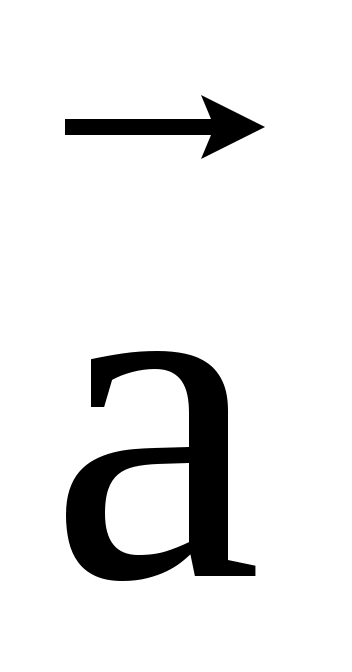 и направленный в сторону конца вектора и направленный в сторону конца вектора 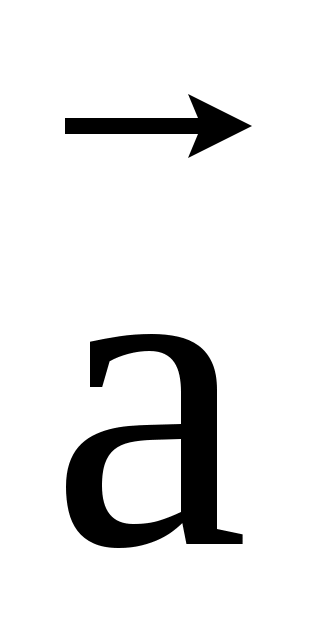 . .
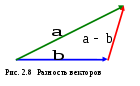
§ 2.4. Базис векторного пространства. Координаты вектора
Понятия линейной комбинации, линейной зависимости и независимости векторов вводятся аналогично тому, как это было сделано для строк матрицы.
Определение. Линейной комбинацией векторов  , ,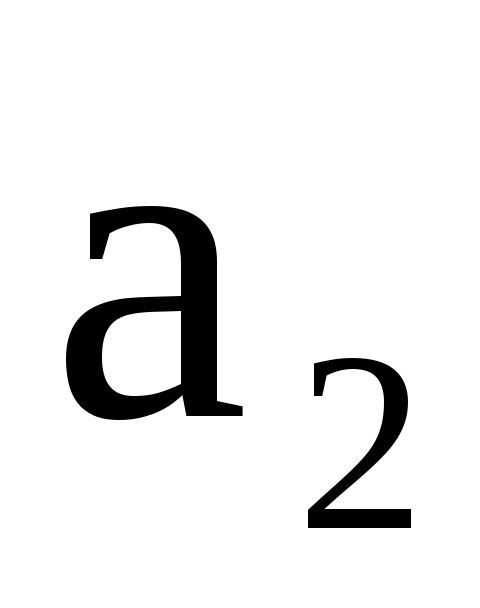 ,..., ,...,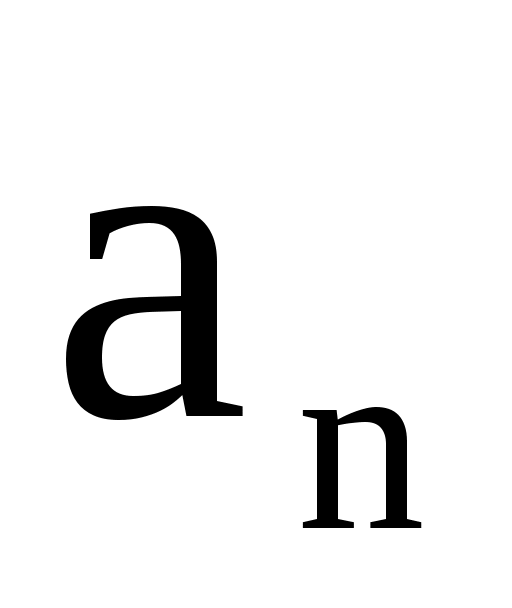 с коэффициентами C1,C2,...,Cn называется вектор C1 с коэффициентами C1,C2,...,Cn называется вектор C1 +C2 +C2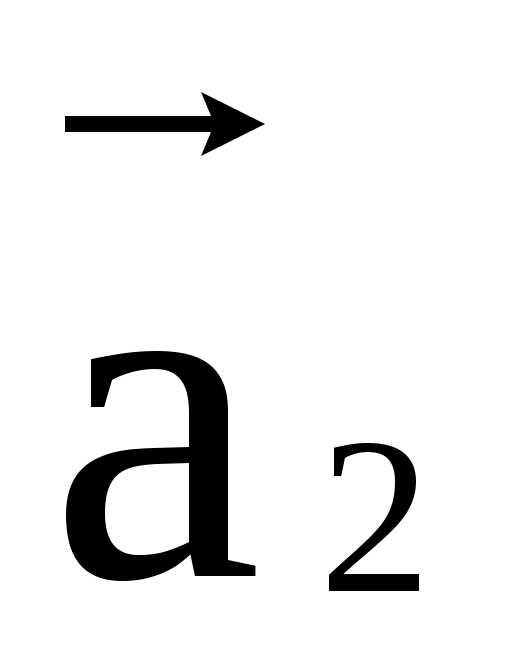 +...+Cn +...+Cn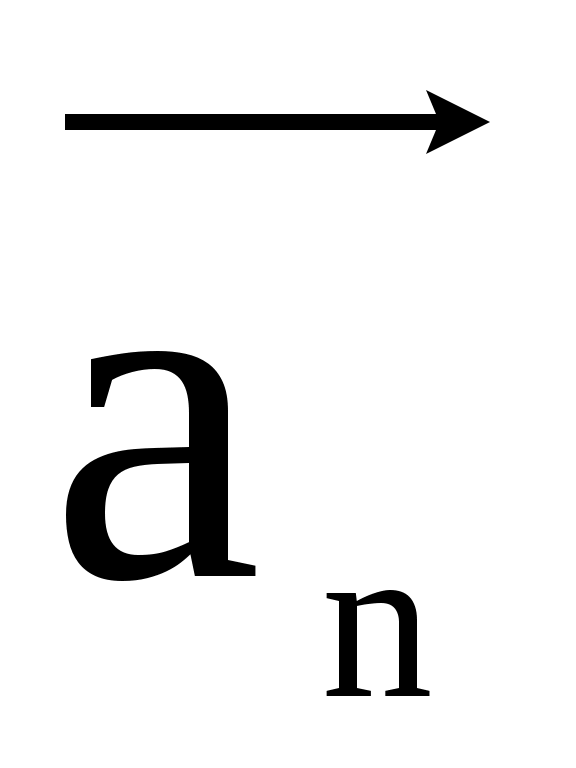 . .
Эта комбинация обладает двумя основными свойствами.
Если векторы  , ,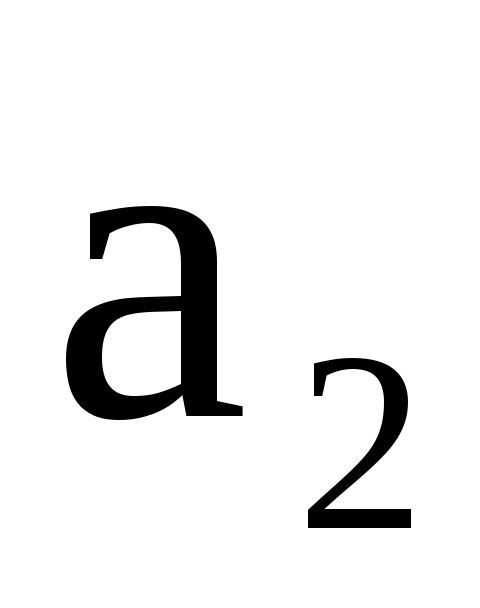 ,..., ,...,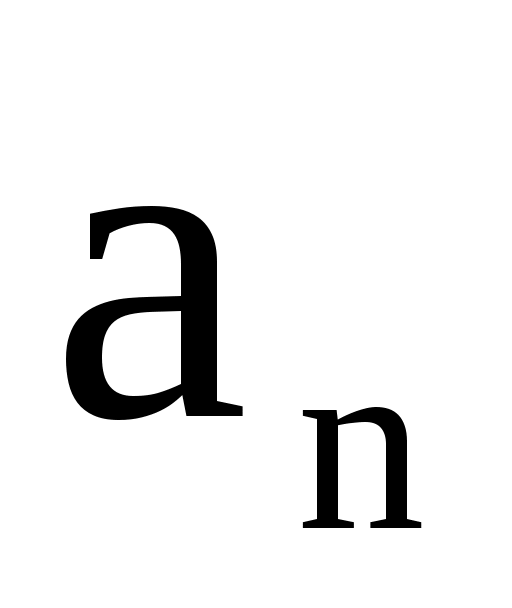 коллинеарны некоторой прямой, то любая их линейная комбинация будет коллинеарна той же прямой. коллинеарны некоторой прямой, то любая их линейная комбинация будет коллинеарна той же прямой.
Векторы  , ,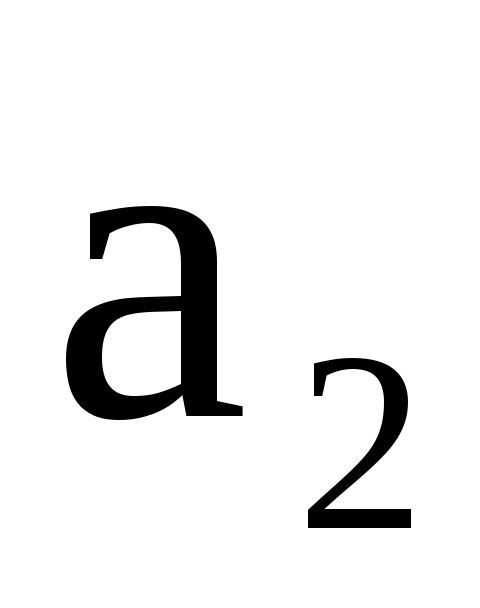 ,..., ,...,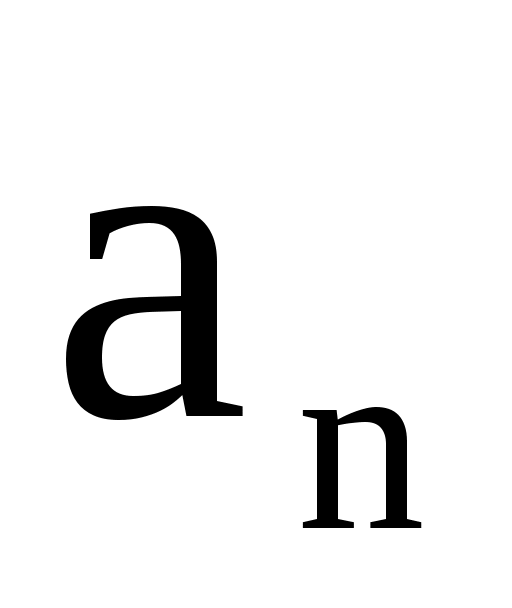 называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если векторы  , ,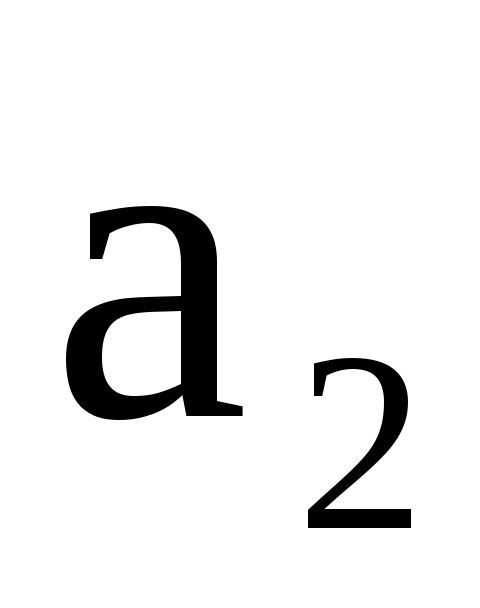 ,..., ,...,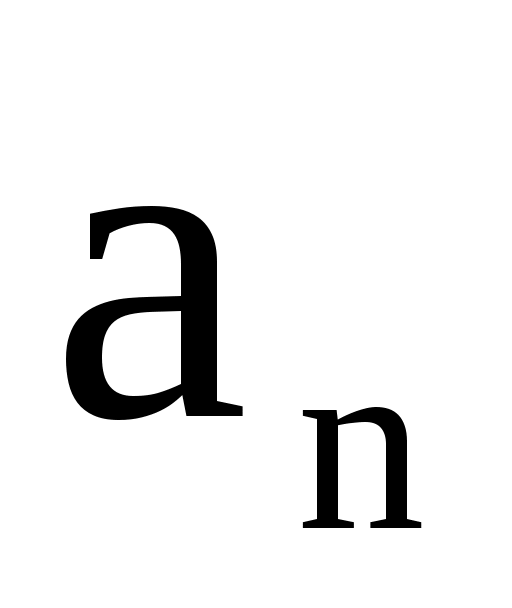 компланарны некоторой плоскости, то любая их линейная комбинация компланарна той же плоскости. компланарны некоторой плоскости, то любая их линейная комбинация компланарна той же плоскости.
Определение. Векторы  , ,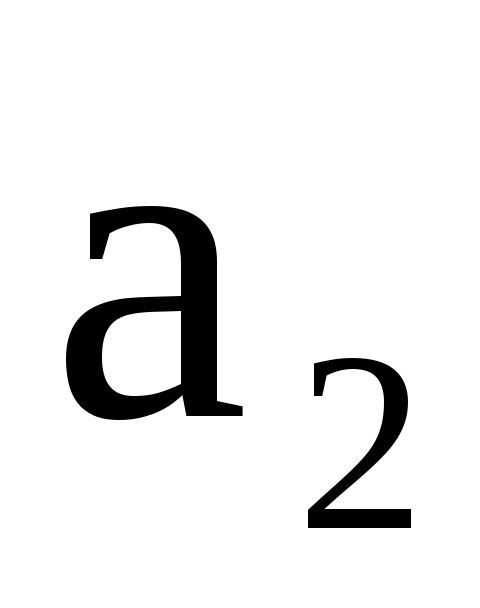 ,..., ,...,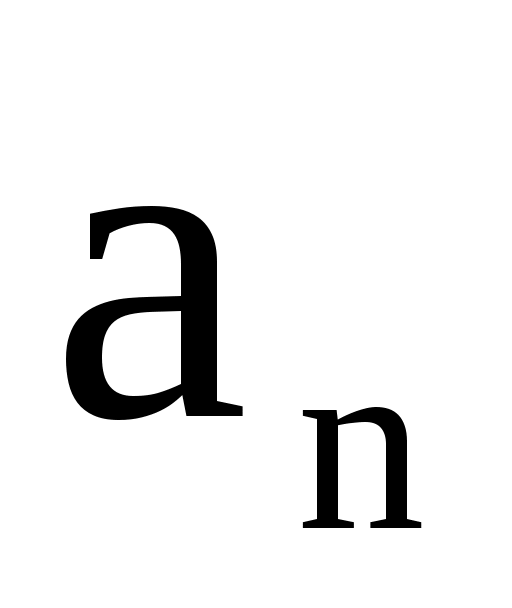 называются линейнозависимыми, если существуют такие числа C1,C2,...,Cn, не все равные нулю, что C1 называются линейнозависимыми, если существуют такие числа C1,C2,...,Cn, не все равные нулю, что C1 +C2 +C2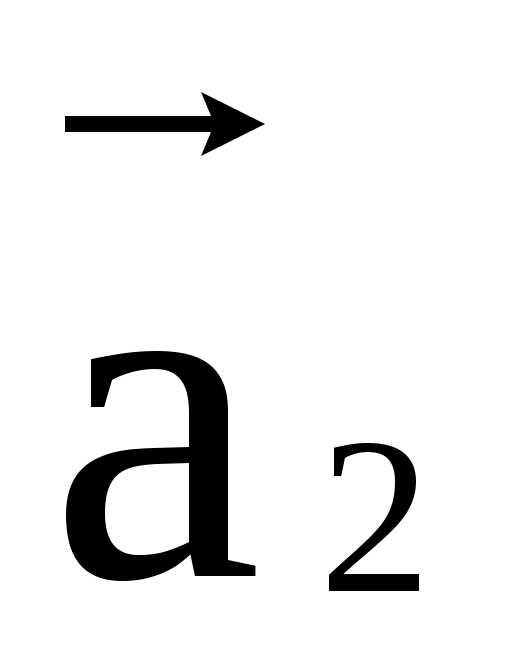 +...+Cn +...+Cn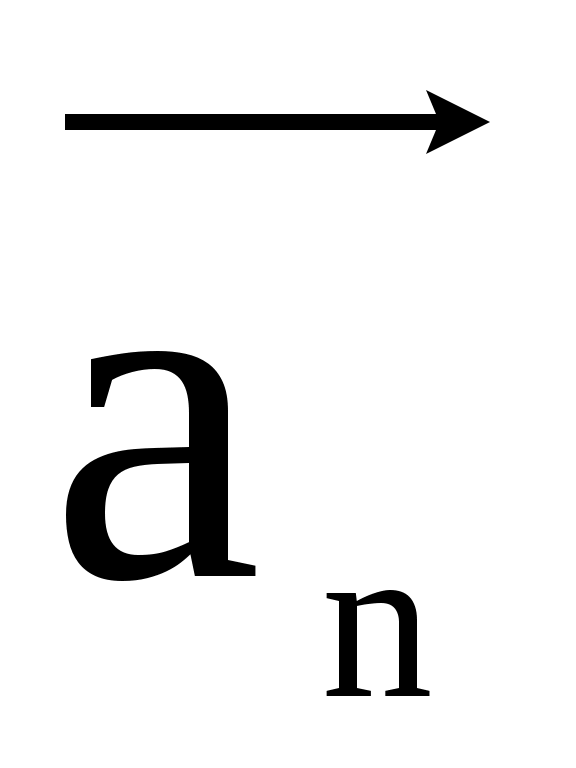 =0 =0
В противном случае векторы  , ,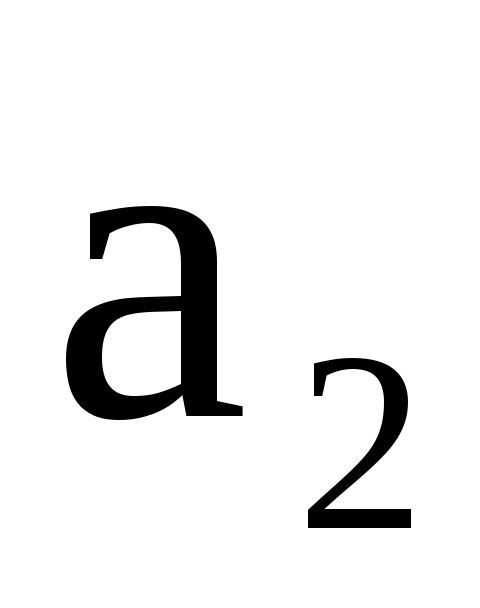 ,..., ,...,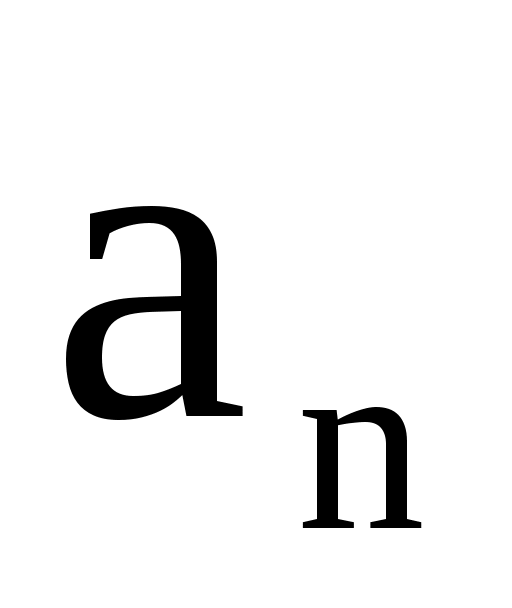 называются линейно независимыми. называются линейно независимыми.
Определение. Совокупность n линейно независимых векторов называется базисом.
Множество всех плоских или пространственных векторов в которых определены операции сложения векторов и умножение вектора на число, являются простейшими примерами векторного пространства.
Определение. Множество векторов, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше семи свойствам называется векторным пространством.
Оказывается, что в любом векторном пространстве всегда можно выбрать несколько векторов, из которых с помощью линейных комбинаций однозначно можно получить любой вектор этого пространства и которые являются базисными.
Определение. Любой ненулевой вектор 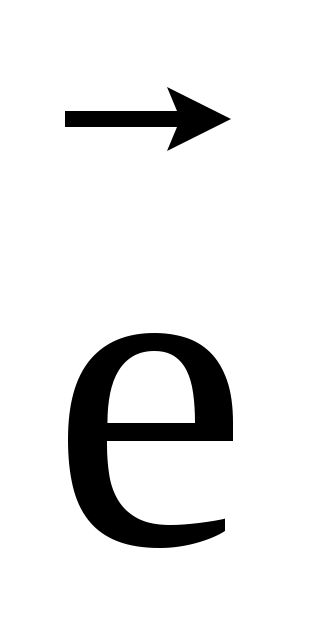 на прямой называется на прямой называется
базисным векторомэтой прямой. Любая пара неколлинеарных векторов 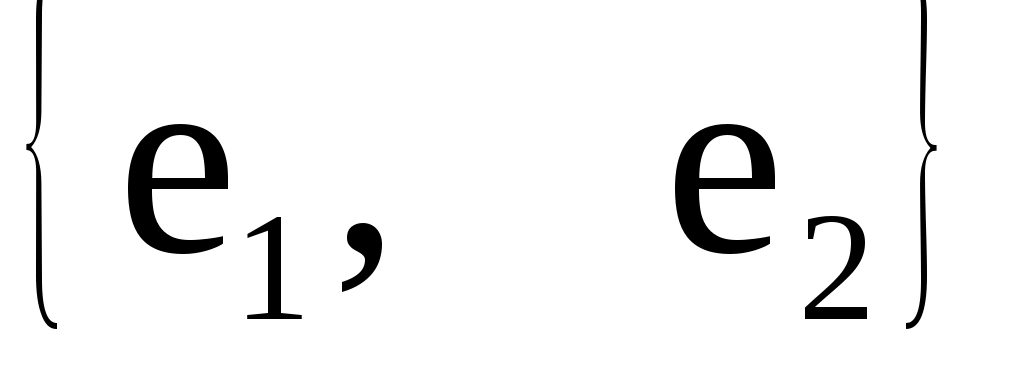 плоскости называется базисом этой плоскости. Любая тройка некомпланарных векторов плоскости называется базисом этой плоскости. Любая тройка некомпланарных векторов 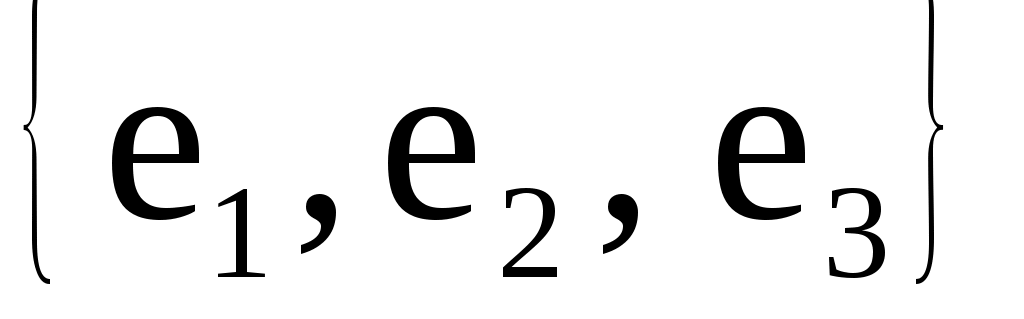 называется базисом пространства. называется базисом пространства.
Теорема о базисе.Любой вектор 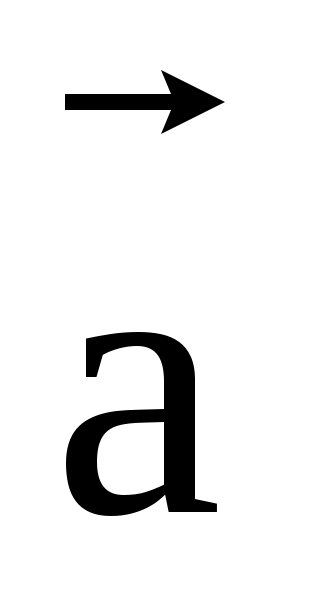 (на прямой, плоскости или в пространстве) единственным образом записывается в виде линейной комбинации соответствующих базисных векторов. То есть, (на прямой, плоскости или в пространстве) единственным образом записывается в виде линейной комбинации соответствующих базисных векторов. То есть,
на прямой: 
на плоскости: 
в пространстве: 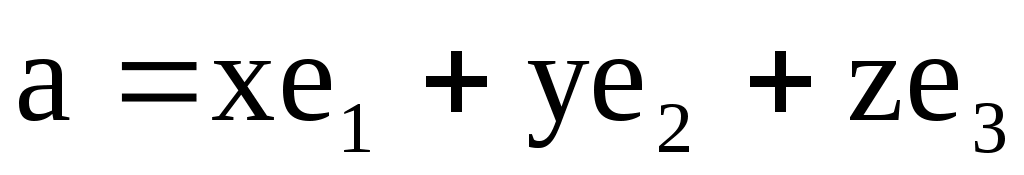
Доказательство.
Случай прямой.
Пусть вектор  лежит на прямой L, лежит на прямой L, 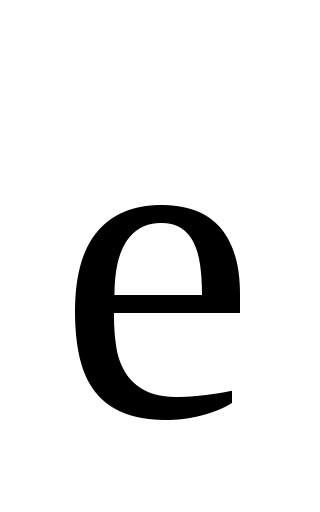 – базисный вектор этой прямой. Отложим вектора – базисный вектор этой прямой. Отложим вектора  и и 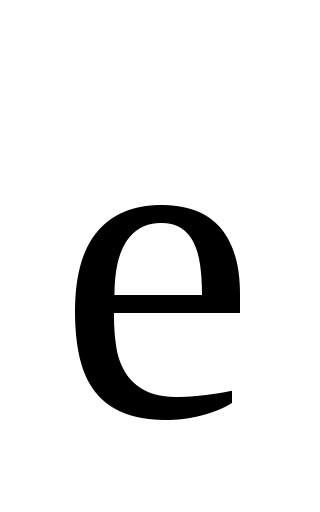 из некоторой точки O на прямой, вектор из некоторой точки O на прямой, вектор 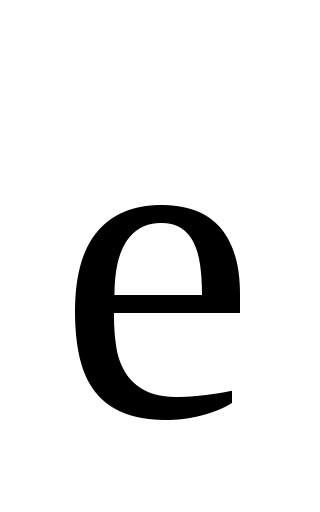 возьмём в качестве масштабного единичного отрезка на L, в результате на L образуется координатная ось. Пусть конец вектора возьмём в качестве масштабного единичного отрезка на L, в результате на L образуется координатная ось. Пусть конец вектора  есть точка A, и x её координата на этой оси, тогда согласно определению произведения вектора на число имеем есть точка A, и x её координата на этой оси, тогда согласно определению произведения вектора на число имеем 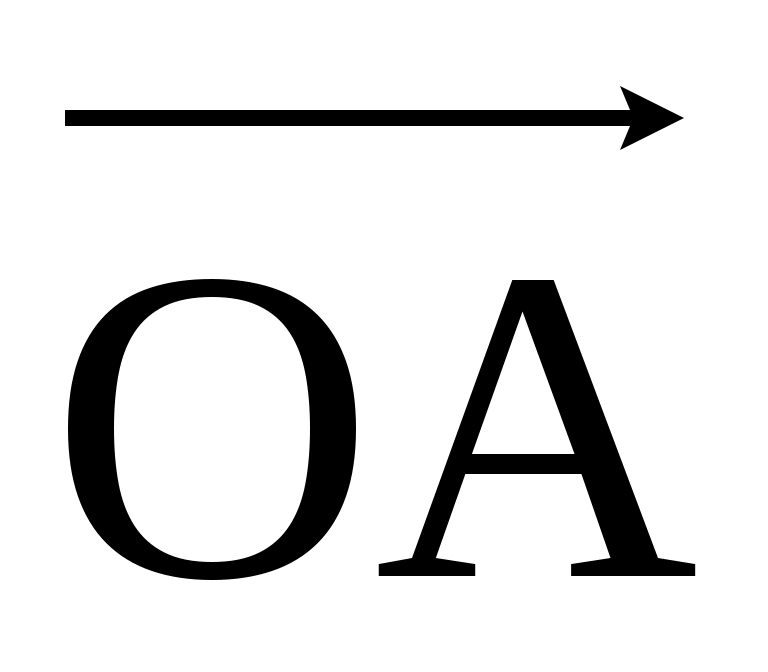 =x =x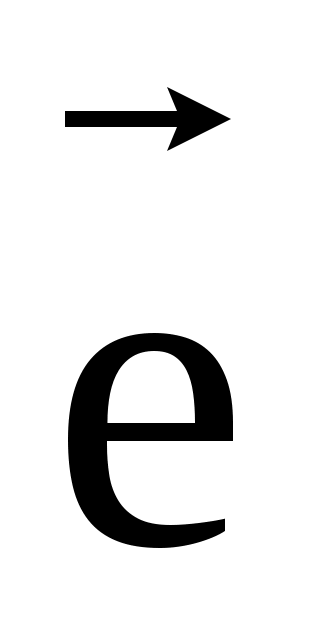 , т.е. , т.е. 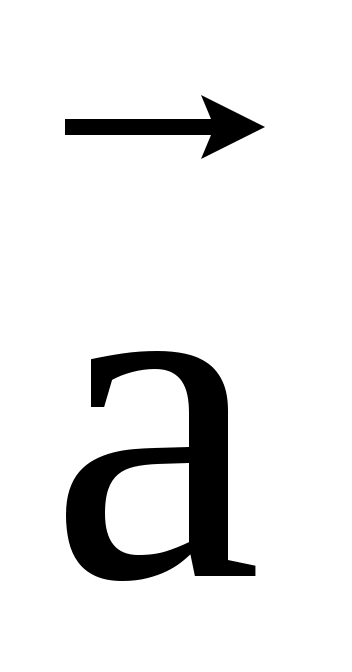 =x =x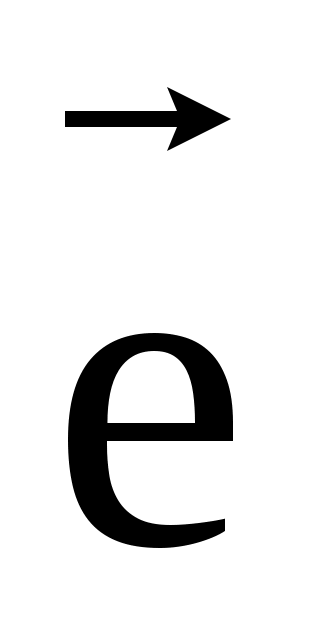 . .
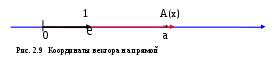
L
Случай плоскости.
Пусть векторы  , ,  и и  лежат в плоскости лежат в плоскости  .Отложим их из некоторой точки O этой плоскости, конец вектора .Отложим их из некоторой точки O этой плоскости, конец вектора  обозначим через A. обозначим через A.
Проведём через вектора  и и  оси Ox и Oy с единичными отрезками оси Ox и Oy с единичными отрезками
 и и  , через точкуA проведём прямые параллельные этим осям, их точки пересечения сOX и Oy обозначим черезA1 и A2 соответственно. , через точкуA проведём прямые параллельные этим осям, их точки пересечения сOX и Oy обозначим черезA1 и A2 соответственно.
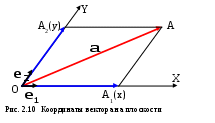
П
Координату точки A1 наOx обозначим через x, а координату точки A2 на Oy – черезy. Тогда используя определение суммы векторов и предыдущий случай получим:  = = = = + + =x =x +y +y . .
3) Случай пространства. Отложим вектора 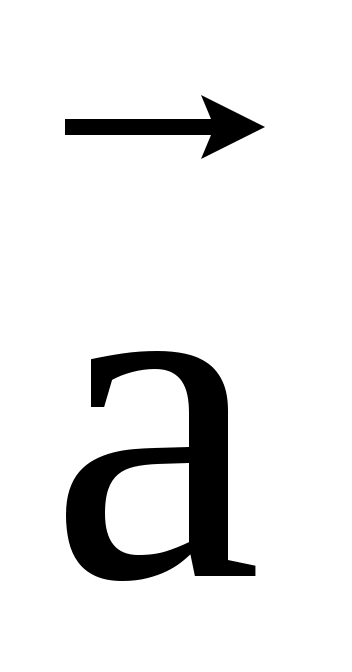 , , 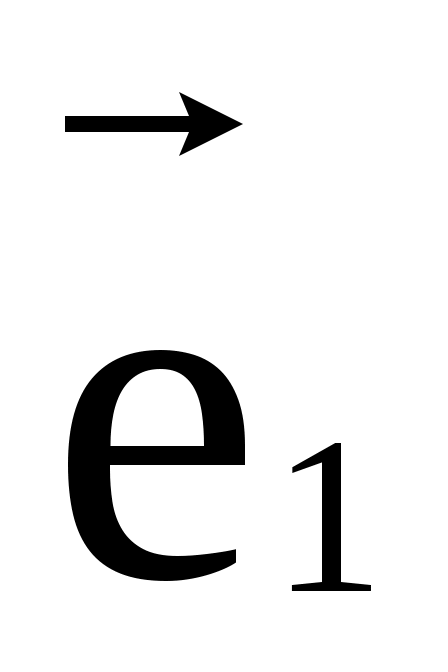 , ,  и и  из некоторой точки O, через вектора из некоторой точки O, через вектора  , ,  , и , и 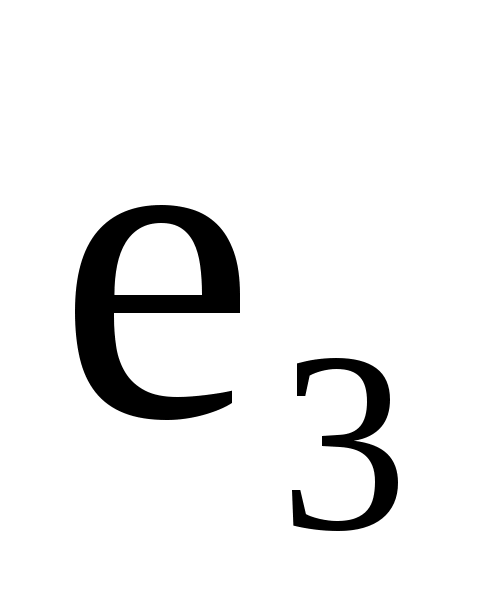 проведём оси Ox, Oy, Oz. Из конца вектора проведём оси Ox, Oy, Oz. Из конца вектора  , точки A проведём три плоскости, параллельные парам осей Ox,Oy; Oy, Oz и Ox, Oz. Их точки пересечения с осями Ox, Oy, Oz обозначим через A1, A2, A3, а координаты этих точек на осях через x, y, z. В результате мы имеем. , точки A проведём три плоскости, параллельные парам осей Ox,Oy; Oy, Oz и Ox, Oz. Их точки пересечения с осями Ox, Oy, Oz обозначим через A1, A2, A3, а координаты этих точек на осях через x, y, z. В результате мы имеем.  = = = =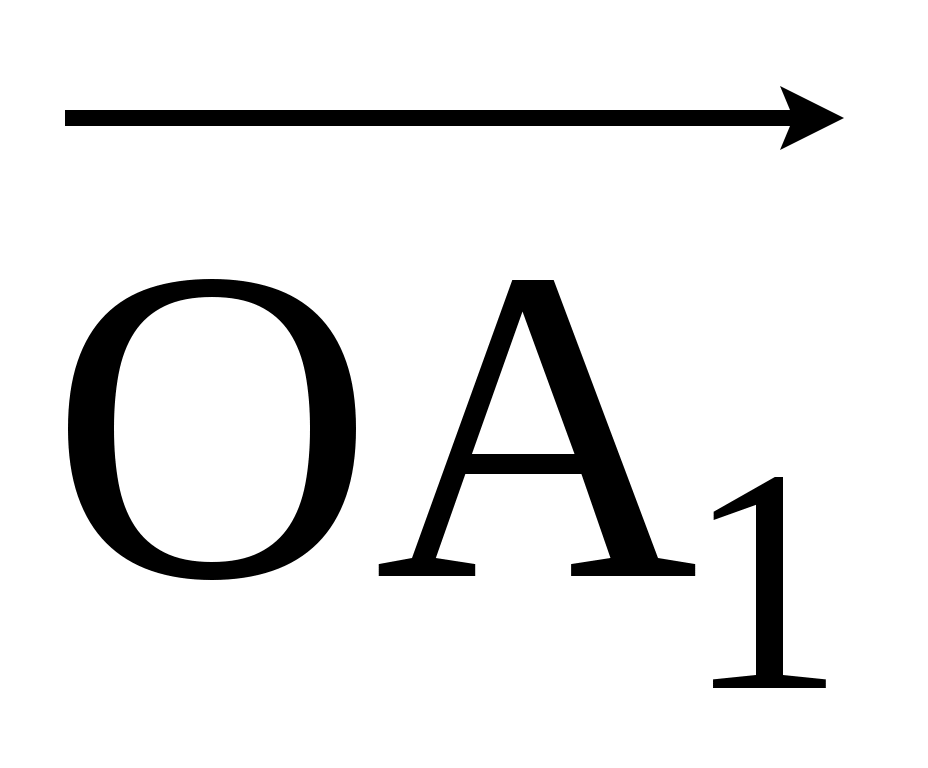 + +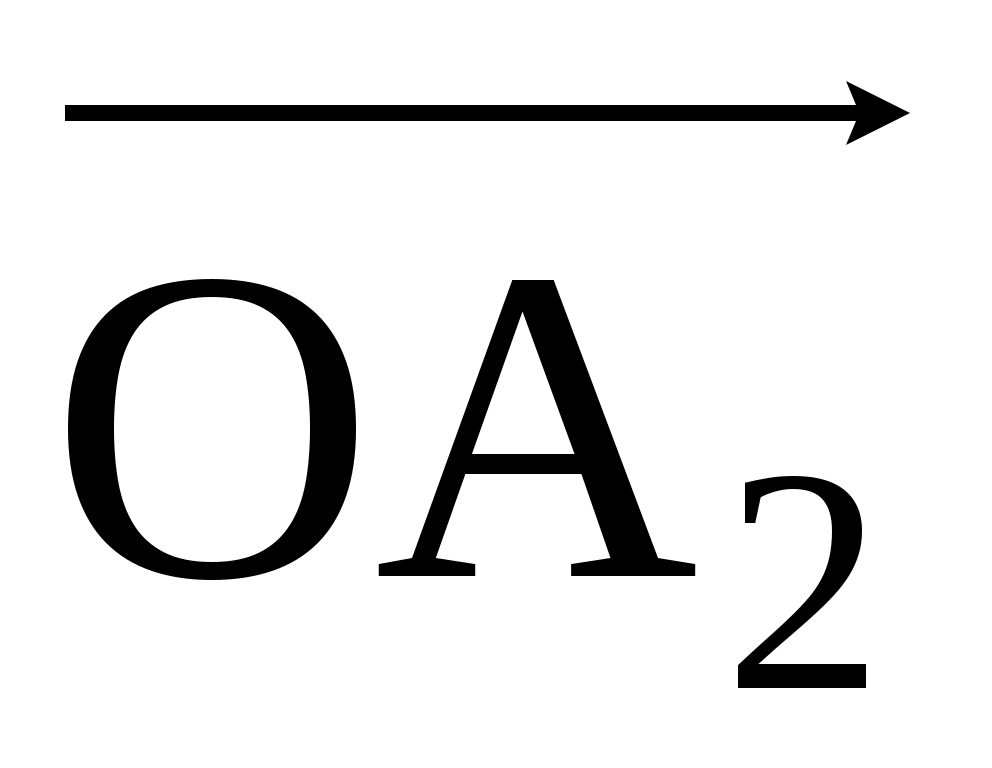 + + =x =x +y +y +z +z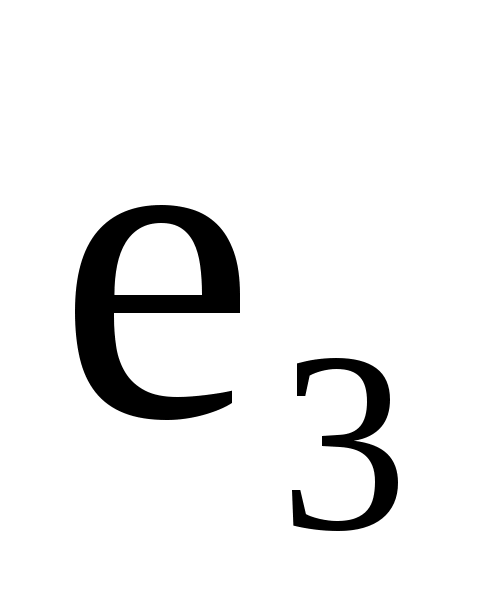 . .
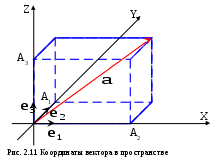
Проверим, что коэффициенты (x, y, z) линейной комбинации определяется однозначно. Допустим противное, пусть вектор  можно записать двумя способами: можно записать двумя способами:  = x1 = x1 +y1 +y1 +z1 +z1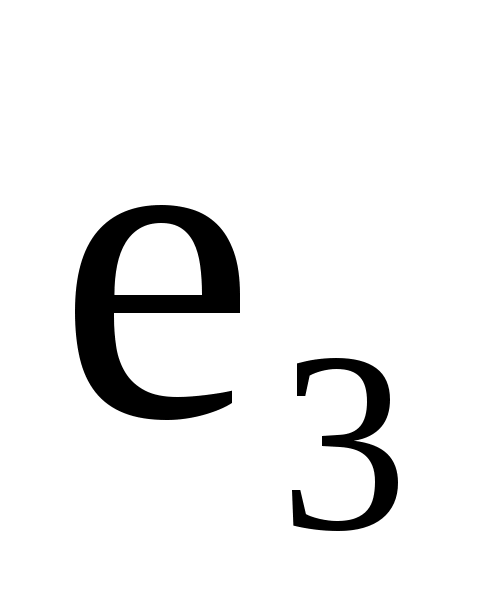 и и  = x2 = x2 +y2 +y2 +z2 +z2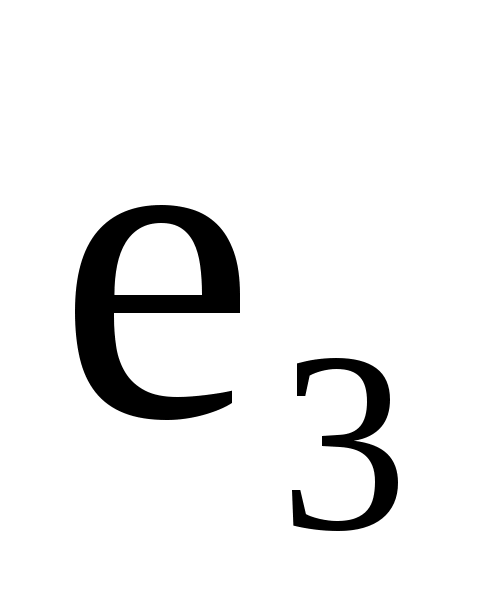 , где x1 x2 или y1y2 , или z1z2. Вычитая из первого равенства второе, получим , где x1 x2 или y1y2 , или z1z2. Вычитая из первого равенства второе, получим 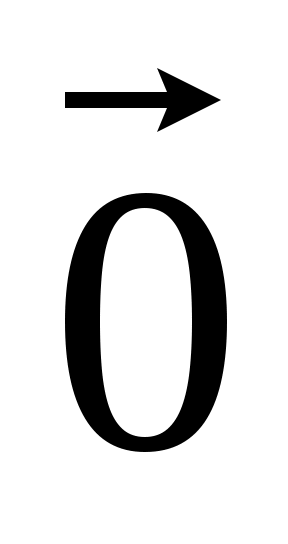 = (x1-x2) = (x1-x2)  + +(y1-y2) + +(y1-y2)  +(z1-z2) +(z1-z2) 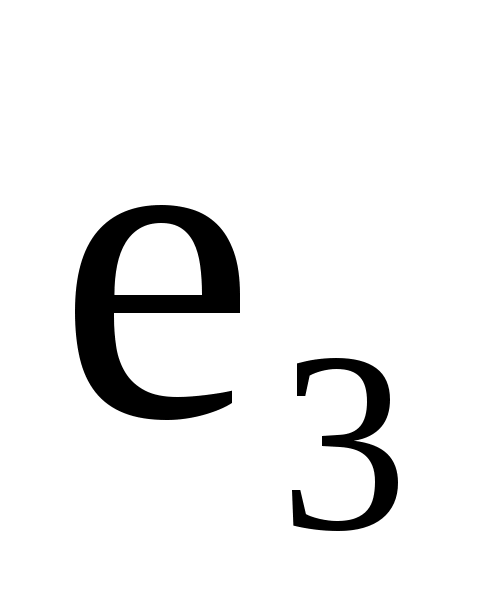 . .
Здесь справа стоит вектор, выражающий диагональ параллелограмма или параллелепипеда, или отрезок на одной из осей Ox, Oy, Oz, который не является нулевым. Противоречие.
Из последнего рассуждения следует, что базисные вектора линейно независимы.
Определение. Коэффициенты линейной комбинации базисных векторов, выражающие вектор  на прямой, в плоскости или в пространстве называются, координатами вектора на прямой, в плоскости или в пространстве называются, координатами вектора  в данном базисе. в данном базисе.
Вектор, лежащий на прямой, имеет одну координату x, на плоскости – две координаты x, y; в пространстве – три координаты x, y, z.
Векторы удобно отождествлять с координатами в некотором выбранном базисе. Так, вектор  в пространстве записывают в виде: в пространстве записывают в виде:
 =(x,y,z) или =(x,y,z) или  ={x,y,z} ={x,y,z}
|
 Скачать 1.14 Mb.
Скачать 1.14 Mb.


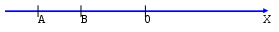
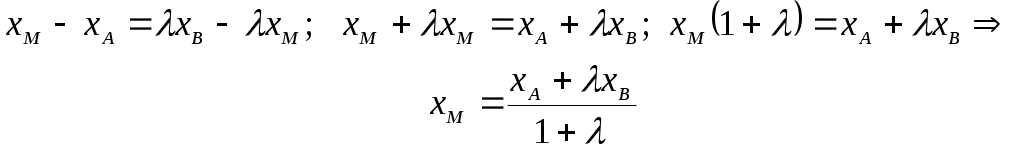
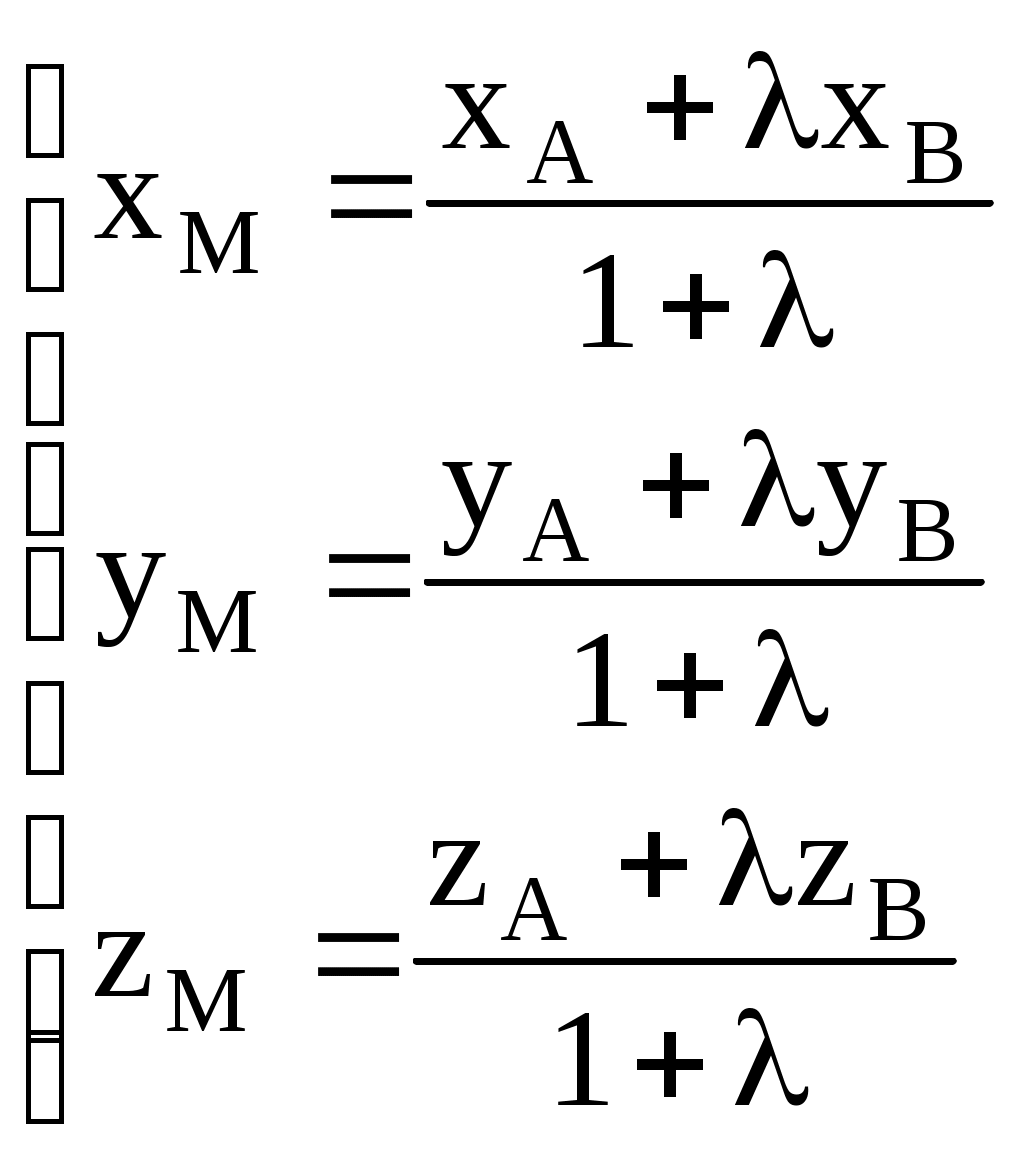
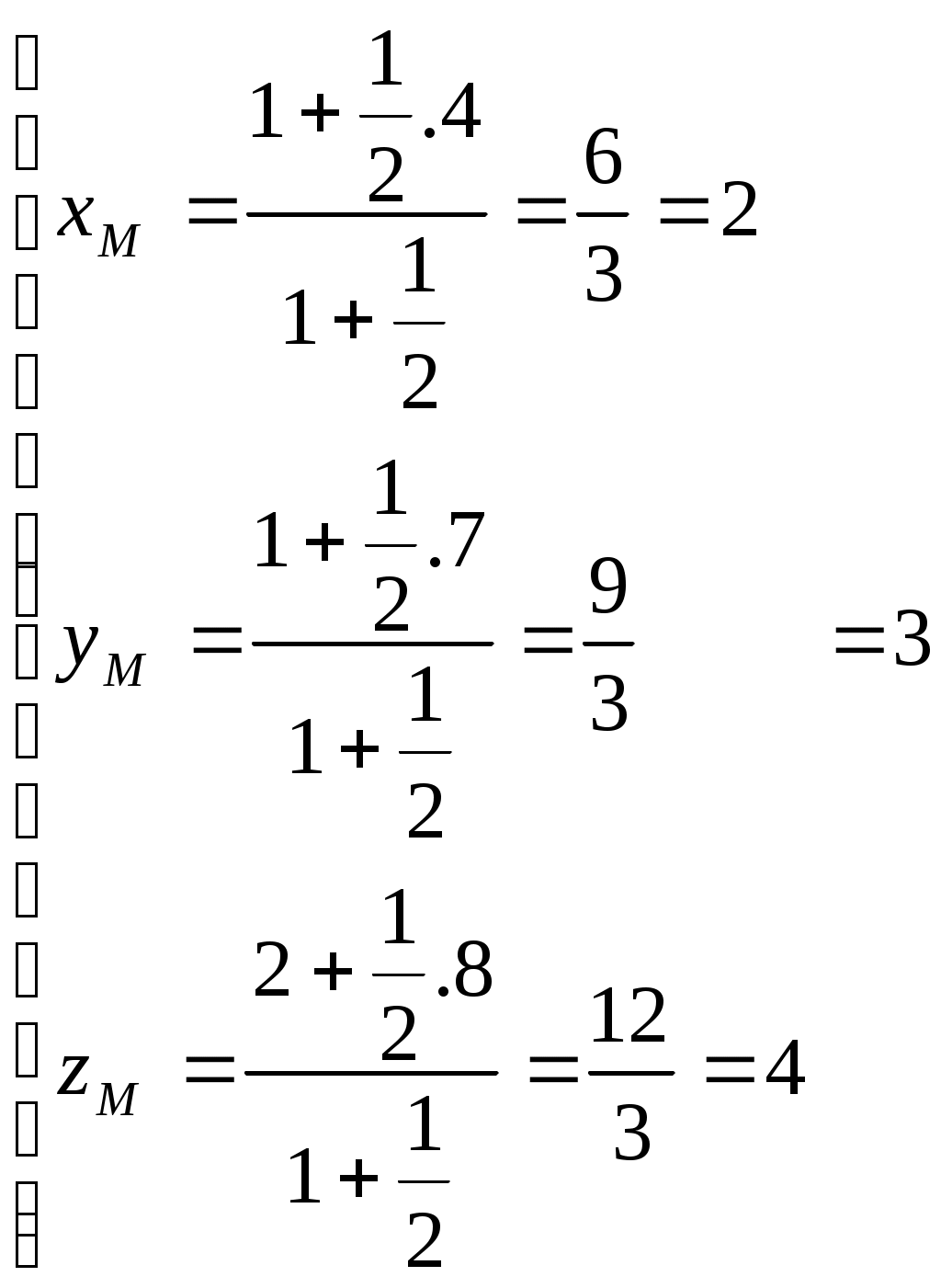 .
.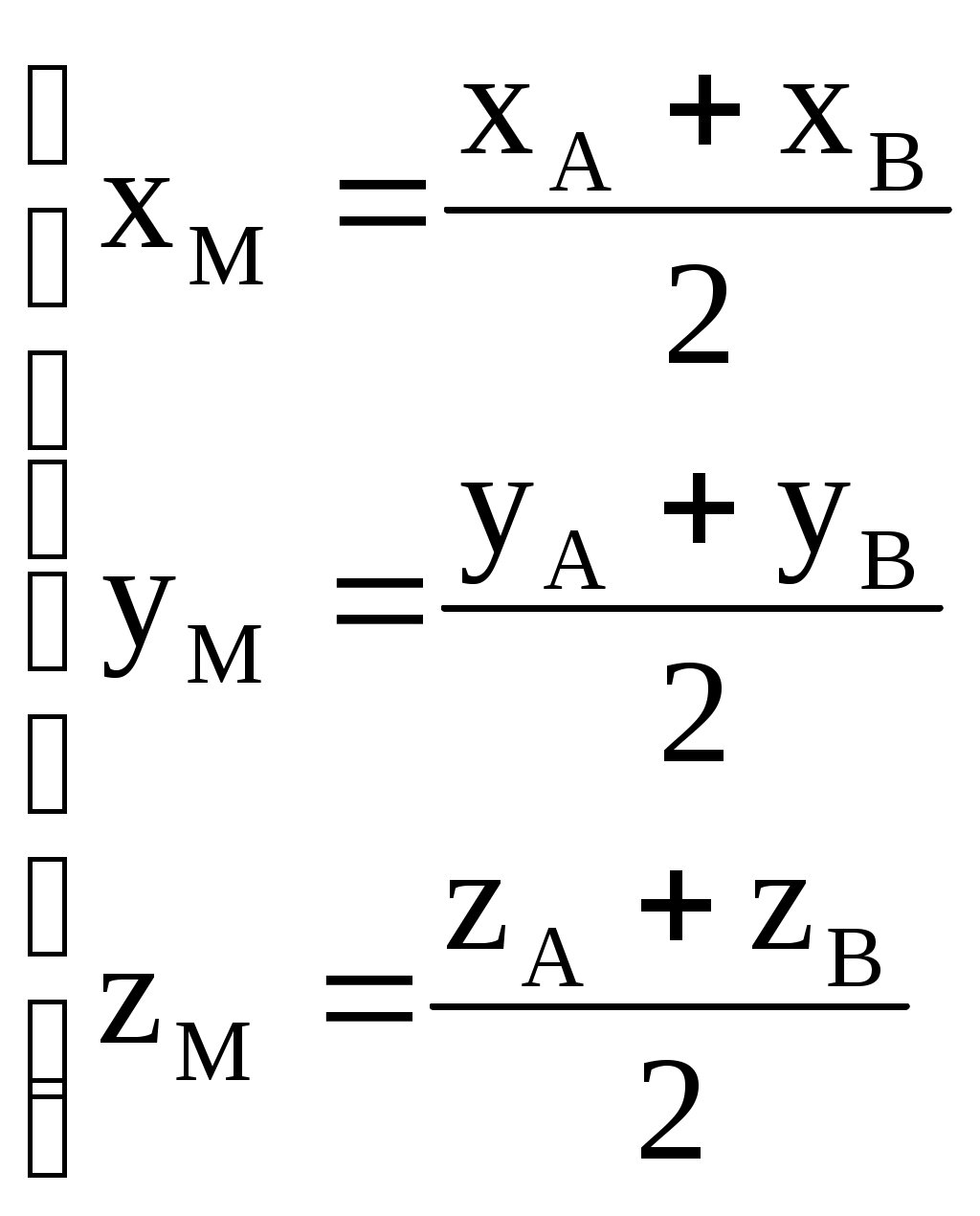 .
.