Динамическое программирование. Динамическое программирование
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
Глава 1. Динамическое программированиеДинамическое программирование представляет собой математический аппарат, позволяющий осуществлять оптимальное планирование (управление) многошаговых управляемых процессов и процессов, зависящих от времени. Задачи динамического программирования называются многоэтапными или многошаговыми. В экономических процессах управление заключается в распределении и перераспределении средств на каждом этапе. Например, выпуск продукции любым предприятием – управляемый процесс, так как он определяется изменением состава оборудования, объемом поставок сырья, величиной финансирования и т.д. Совокупность решений, принимаемых в начале каждого года планируемого периода по обеспечению предприятия сырьем, замене оборудования, размерам финансирования и т.д., является управлением. 1. 1. Постановка задачи динамического программированияОсобенности задач динамического программированияДинамическое программирование представляет собой поэтапное планирование многошагового процесса, при котором на каждом этапе, учитывая развитие всего процесса, оптимизирует только один шаг, т.е. при принятии решения учитывается будущее. Однако в каждом процессе имеется последний 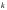 -й шаг, принятие решения на котором не зависит от будущего. Поэтому на этом шаге выбирают управление, позволяющее получить наибольший эффект. Спланировав этот шаг, к нему можно присоединить предпоследний -й шаг, принятие решения на котором не зависит от будущего. Поэтому на этом шаге выбирают управление, позволяющее получить наибольший эффект. Спланировав этот шаг, к нему можно присоединить предпоследний  -й шаг, к которому, в свою очередь, -й шаг, к которому, в свою очередь,  -й и т.д. В конечном итоге приходят в начальное состояние системы -й и т.д. В конечном итоге приходят в начальное состояние системы  . . Для того чтобы спланировать 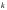 -й шаг, надо знать состояние системы на -й шаг, надо знать состояние системы на  -м шаге. Если состояние системы на -м шаге. Если состояние системы на  -м шаге неизвестно, то, исходя из характера данного процесса, делают различные предположения о возможных состояниях системы на этом шаге. Для каждого предположения выбирают оптимальное управление на последнем, -м шаге неизвестно, то, исходя из характера данного процесса, делают различные предположения о возможных состояниях системы на этом шаге. Для каждого предположения выбирают оптимальное управление на последнем, 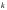 -м, шаге. Такое оптимальное управление называется условно оптимальным. -м, шаге. Такое оптимальное управление называется условно оптимальным. Общая постановка задачи динамического программированияПусть некоторая физическая управляемая система  находиться в первоначальном состоянии находиться в первоначальном состоянии . С течением времени ее состояние меняется и система приходит в конечное состояние . С течением времени ее состояние меняется и система приходит в конечное состояние  . С процессом изменения состояния системы связан некоторый численный критерий . С процессом изменения состояния системы связан некоторый численный критерий  . Необходимо так организовать процесс, чтобы критерий достиг оптимального значения. . Необходимо так организовать процесс, чтобы критерий достиг оптимального значения.Обозначим множество возможных управлений через  . Тогда задача состоит в том, чтобы из множества возможных управлений . Тогда задача состоит в том, чтобы из множества возможных управлений  найти такое управление найти такое управление  , которое позволит перевести систему , которое позволит перевести систему  из начального состояния из начального состояния  в конечное в конечное  так, что критерий так, что критерий  принимает оптимальное значение принимает оптимальное значение  . .Принцип оптимальности БеллманаОбщая идея метода динамического программирования состоит в том, что в одном направлении проводится пошаговая условная оптимизация, а в другом направлении безусловная оптимизация. Критерий выбора условно оптимальных решений состоит в следующем принципе оптимальности, сформулированным американским математиком Р. Беллманом (1920-1985), автором метода динамического программирования: Каково бы ни было состояние системы  перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным. перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным. |
