Билинейные формы Шестаков. Білінійні та квадратичні функції С. С. Шестаков. Конспект лекцій для студентів заочного відділенння
 Скачать 1.43 Mb.
|
|
Конспект лекцій для студентів заочного відділенння факультету кібернетики Київського національного університету імені Тараса Шевченка Білінійні та квадратичні функції Шестаков С.С., канд. ф.- м. наук, Тмєнова Н.П., канд. ф.- м. наук Київ - 20011 Зміст Білінійні функції та білінійні форми………………………………………………2 Матриця білінійної функції в базисі………………………………………………3 Зв’язок матриць білінійної функції в різних базисах…………………………….5 Симетричні та кососиметричні білінійні функції………………………………...7 Квадратичні функції та квадратичні форми………………………………………8 Два способи завдання квадратичних функцій……………………………………9 Зведення квадратичної функції до канонічного вигляду……………………….10 Метод Лагранжа (метод виділення повних квадратів)………………………….12 Метод Якобі………………………………………………………………………..15 Закон інерції квадратичних форм………………………………………………..20 Додатні квадратичні функції……………………………………………………..22 Критерій Сильвестера……………………………………………………………22 Застосування теорії симетричних матриць до теорії квадратичних функцій...25 Алгоритм зведення квадратичної функції до канонічного вигляду ортогональним перетворенням змінних…………………………………………26 Класифікація поверхонь другого порядку………………………………………27 Список рекомендованої літератури………………………………………………….33 Предметний вказівник………………………………………………………………..34 Білінійні функції та білінійні форми Нехай  - векторний простір над полем  . Відображення  декартового добутку  у поле називається білінійною функцією, якщо виконуються умови:1.  ;2.  ;3.  ;4.  .Таким чином, функція білінійна, якщо при фіксованому другому аргументі вона лінійна за першим і при фіксованому першому вона лінійна за другим. Прикладом білінійної функції є скалярний добуток у евклідові просторі. Але в загальному випадку  .Припустимо тепер, що - скінченновимірний простір,  - деякий фіксований базис простору,  - довільні вектори, які в даному базисі задаються координатами:  . Тоді  .Позначимо   ,тоді  .Сума такого вигляду називається білінійною формою від змінних  . Таким чином, можна зробити висновки:1. На скінченновимірному просторі при фіксованому базисі будь-яка білінійна функція задається деякою білінійною формою. 2. При фіксованому базисі  білінійна функція  на скінченновимірному просторі задається набором чисел  , де  . У цьому розумінні часто поняття білінійної функції заміняється поняттям білінійної форми. Зрозуміло, що при різних фіксованих базисах білінійна функція задається різними білінійними формами, тому кажуть про вигляд білінійної форми в різних базисах.Матриця білінійної функції в базисі Припустимо, що 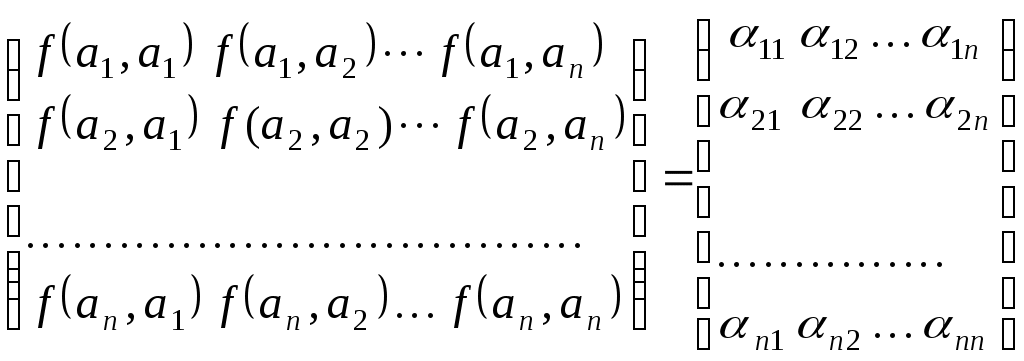- білінійна функція на просторі над полем ,  - деякий фіксований базис простору . Матрицею білінійної функції у базисі називається матриця =  .Матриця білінійної функції в даному базисі цілком визначає білінійну функцію. Нехай 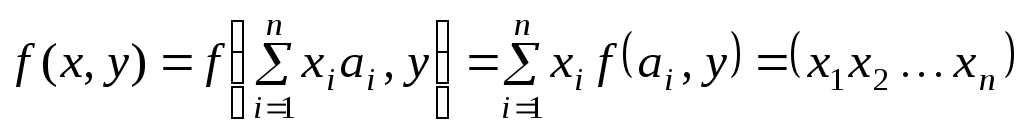 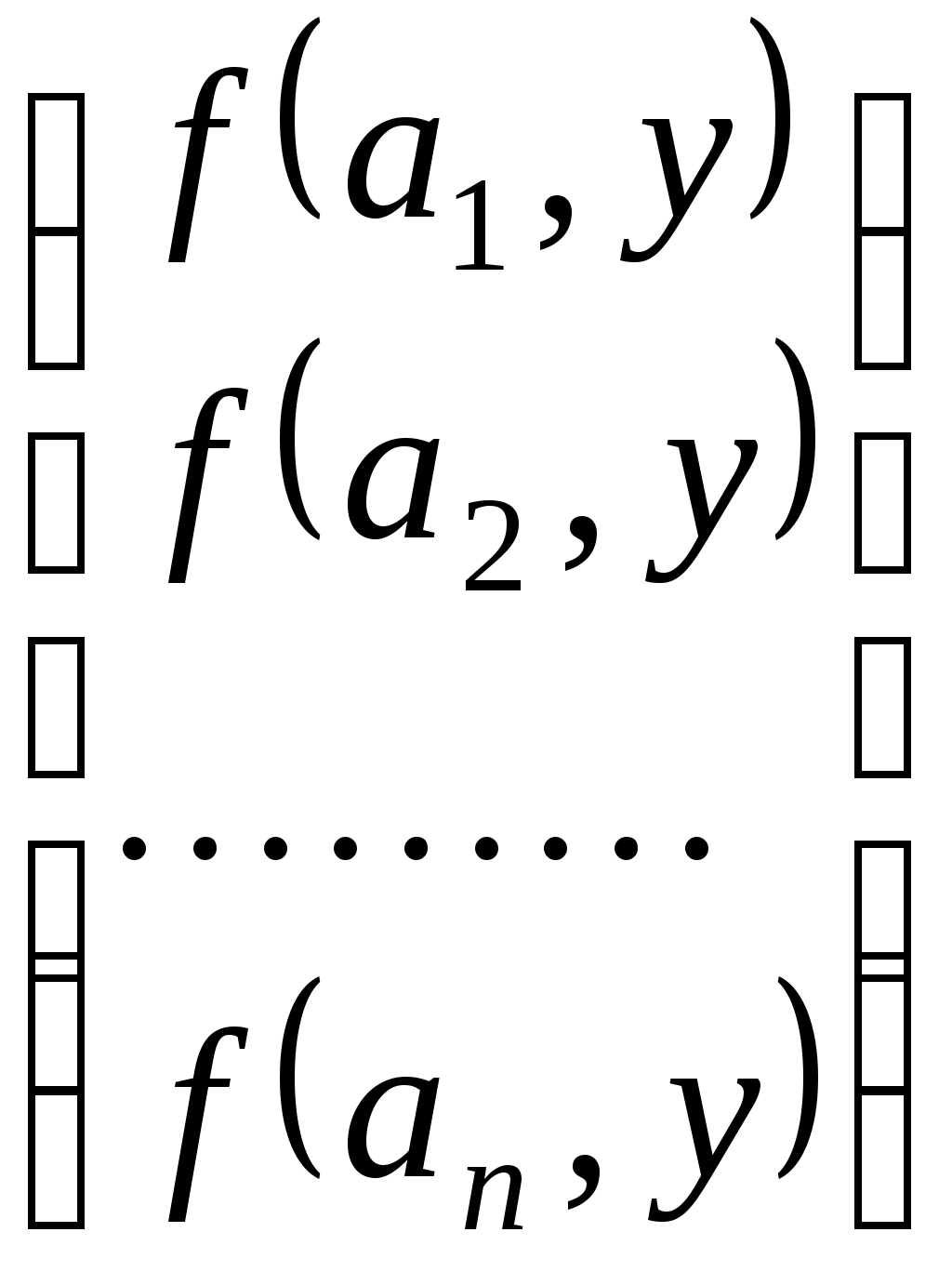- довільні вектори, які в базисі задаються такими координатами:  . Знайдемо значення функції  на векторах    .Далі, 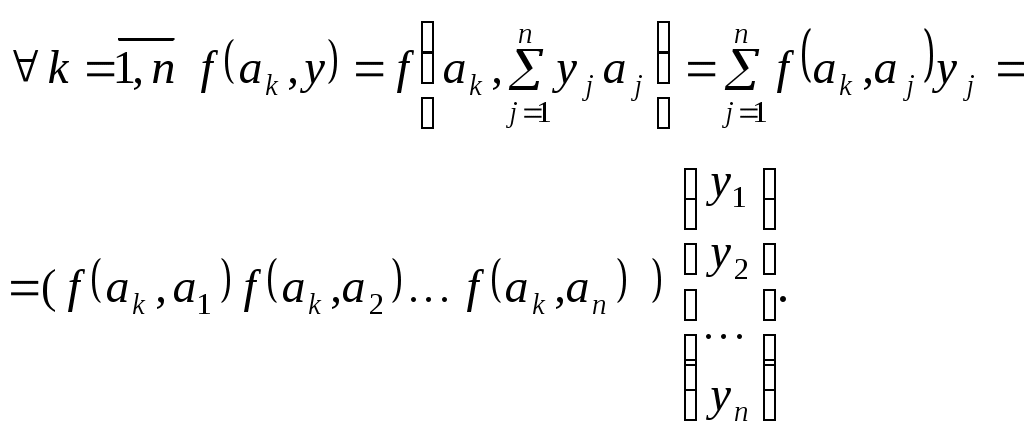 Таким чином, виконуються рівності 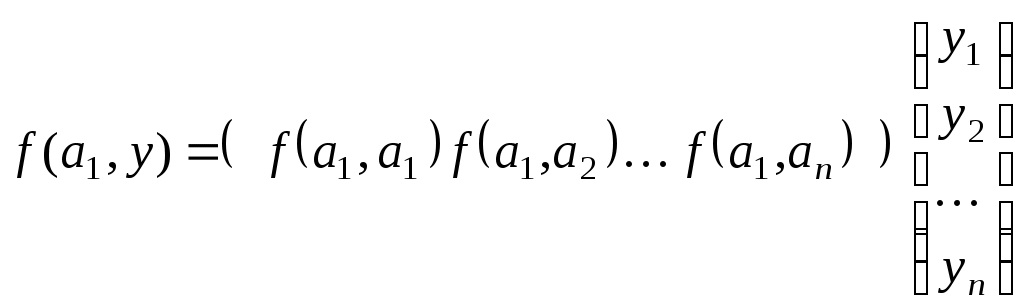 ; 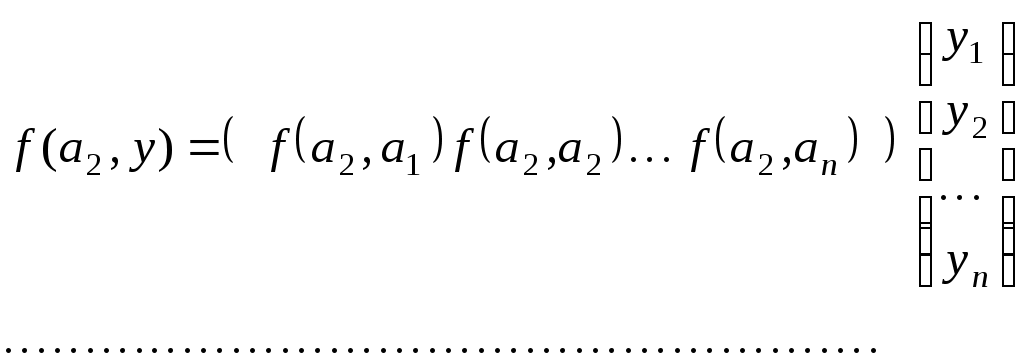 ; 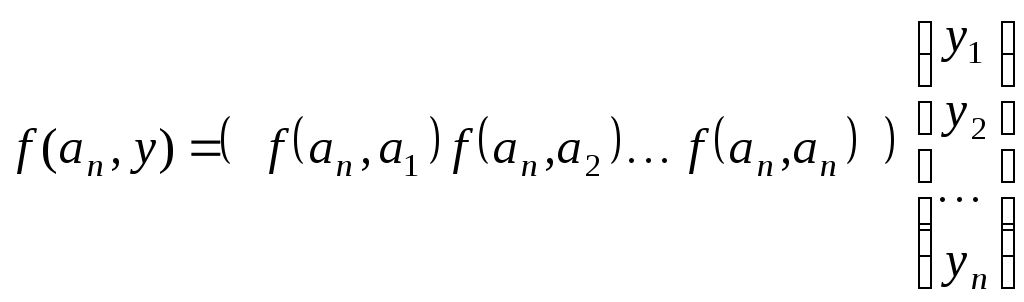.Рівності можемо переписати в матричному вигляді: 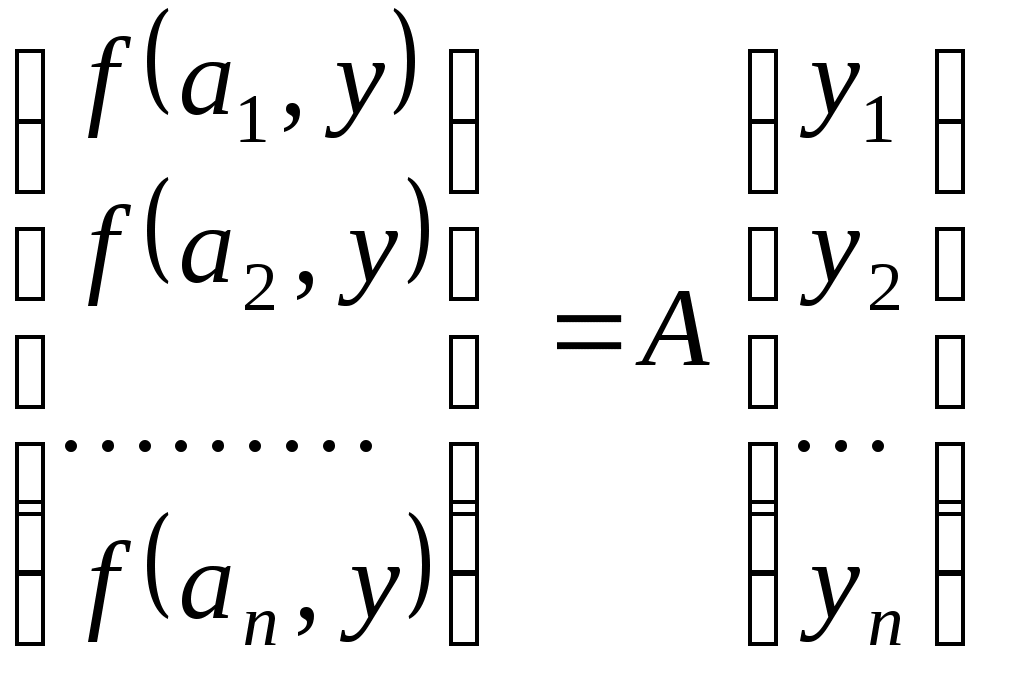 .Звідси: 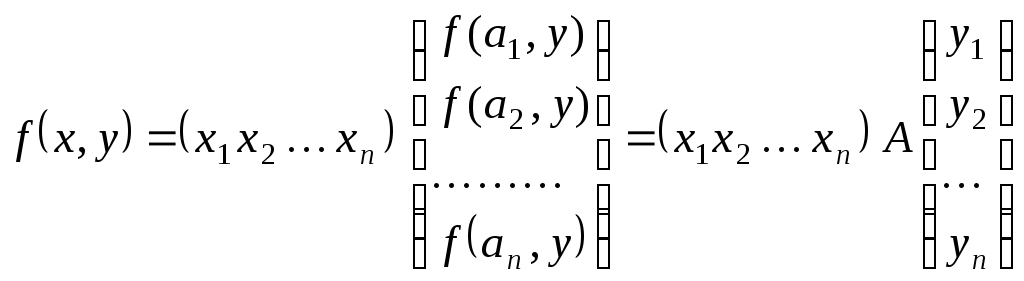 .Таким чином, можна зробити висновок: якщо - матриця білінійної функції у базисі  , вектори  задаються координатами в цьому базисі  ,то значення білінійної функції 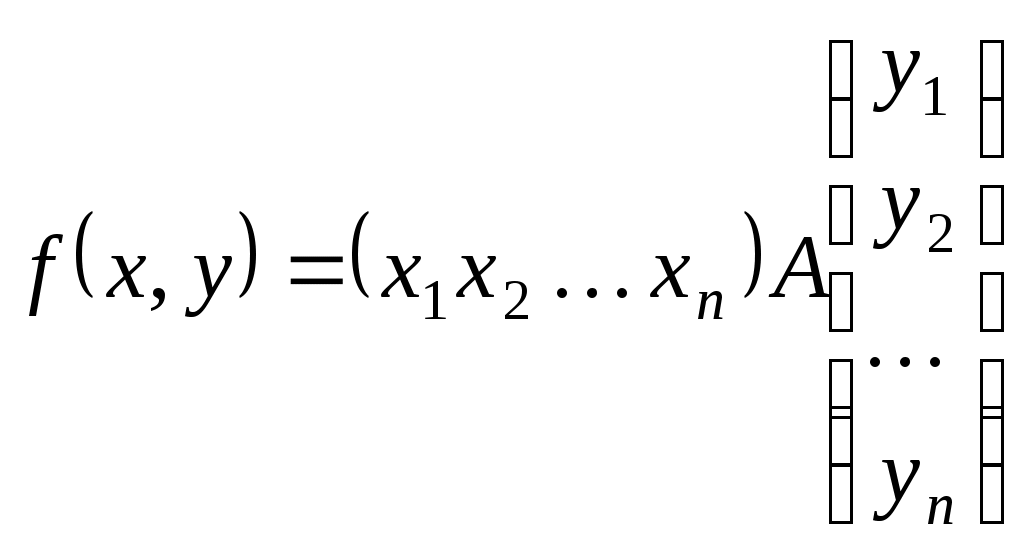на векторах  можна знайти за формулою .Зв’язок матриць білінійної функції в різних базисах Теорема. Нехай білінійній функції  на скінченновимірному просторі над полем у базисі відповідає матриця  , а в базисі  - матриця  ,  - матриця переходу від базису до базису . Тоді  .Доведення. Нехай - дові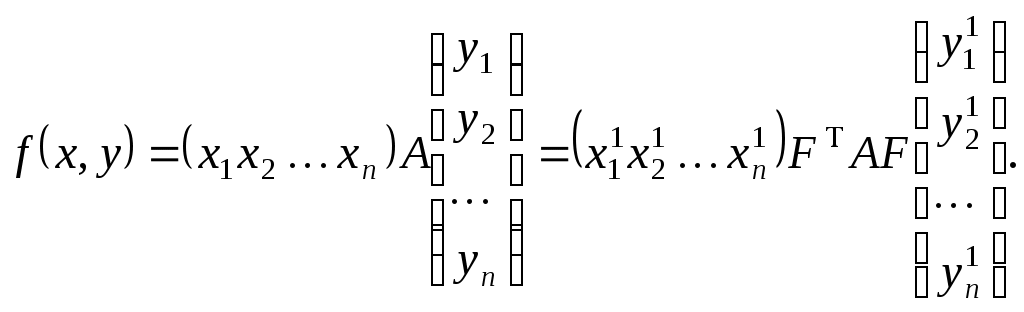льні вектори, які в базисі задаються координатами  а в базисі - координатами  . Оскільки - матриця переходу від базису до базису , то виконуються рівності  Тоді  З іншого боку, 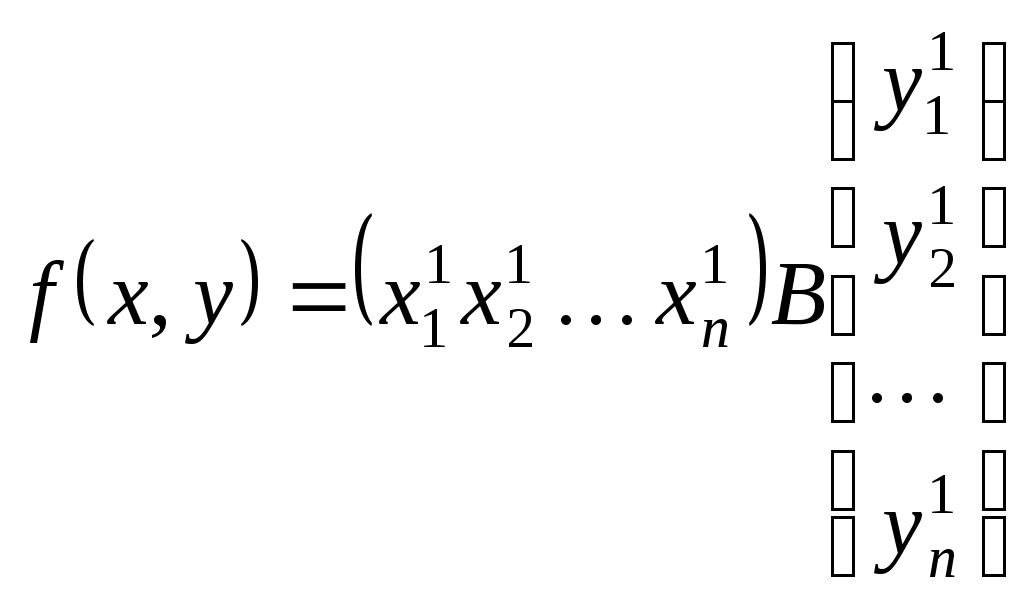 .Покажемо, що 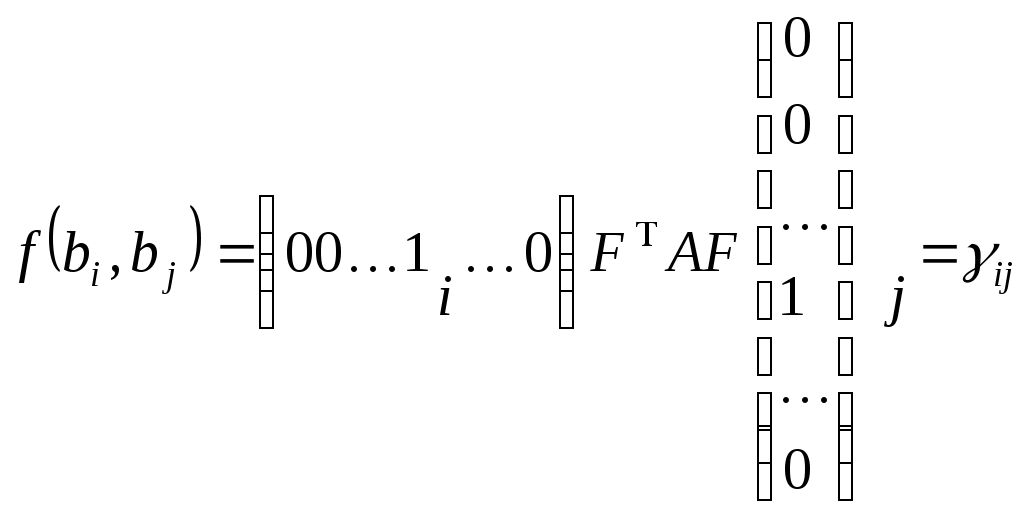. Припустимо, що  , і покажемо, що  . Зафіксуємо індекси  . Тоді  . З іншого боку,  .Тобто,  .Наслідок. Ранг матриці білінійної функції не залежить від вибору базису. Доведення. Якщо  - матриці білінійної функції у різних базисах, то для деякої невиродженої матриці . Як відомо, домноження матриці зліва або справа на невироджену матрицю не змінює її рангу. Тому ранги матриць  рівні.З останнього наслідку випливає коректність наступного означення. Означення. Рангом білінійної функції на скінченновимірному просторі називається ранг її матриці в деякому базисі. Означення. Квадратні матриці називаються конгруентними, якщо існує невироджена матриця така, що . У теоремі було доведено, що матриці білінійної функції в різних базисах конгруентні. Матриця білінійної функції в даному базисі цілком задає цю функцію. З іншого боку, нехай 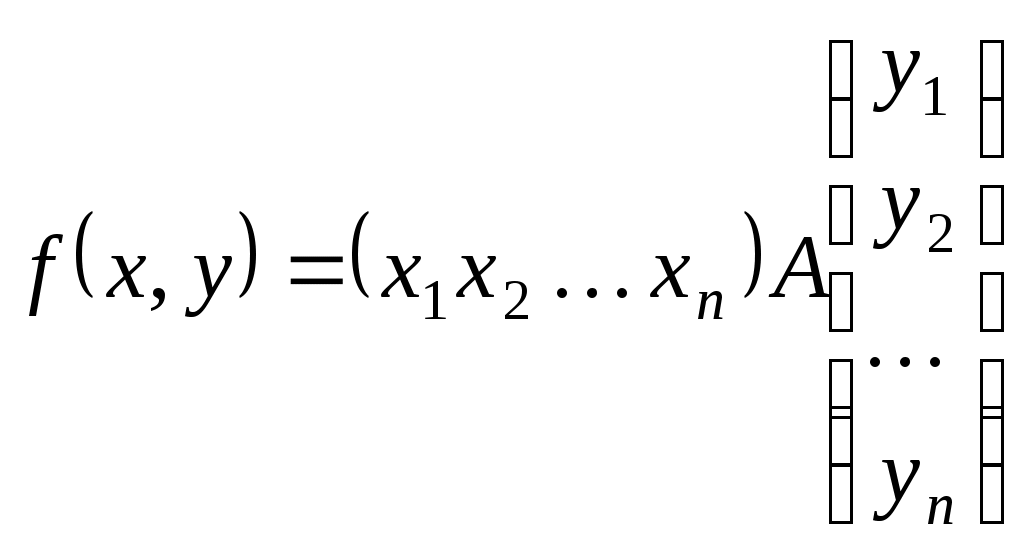- квадратна матриця з дійсними елементами порядку  - векторний простір над полем розмірності  , тоді матриця задає на просторі деяку білінійну функцію. Дійсно, зафіксуємо деякий базис простору  - довільні вектори, які в цьому базисі задаються такими координатами:  . Покладемо . Функція є білінійною функцією на просторі , якій у даному базисі відповідає матриця .Таким чином, при фіксованому базисі простору розмірності між білінійними функціями на цьому просторі і квадратними матрицями з дійсними елементами порядку існує взаємнооднозначна відповідність.Симетричні та кососиметричні білінійні функції Означення. Білінійна функція  на просторі називається симетричною, якщо  .Припустимо, що - скінченновимірний простір, - деякий фіксований базис простору. Тоді  , тобто, матриця симетричної білінійної функції в будь-якому базисі симетрична. Прикладом симетричної білінійної функції є скалярний добуток у евклідові просторі.Зрозуміло, що на просторі розмірності будь-яка симетрична матриця порядку задає симетричну білінійну функцію.Означення. Білінійна функція на просторі називається кососиметричною, якщо  .Означення. Квадратна матриця називається кососиметричною, якщо  . Припустимо, що - кососиметрична білінійна функція на скінченновимірному векторному просторі  - деякий фіксований базис простору. Тоді  . Тобто, в будь-якому базисі кососиметричній білінійній функції відповідає кососиметрична матриця.Зрозуміло також, що для кососиметричної білінійної функції виконується:  .Дослідження довільних білінійних функцій у певному розумінні зводиться до дослідження симетричних та кососиметричних білінійних функцій. Зрозуміло, що існують білінійні функції, які не є симетричними або кососиметричними. Нехай - довільна білінійна функція на просторі ,покладемо  .Оскільки сума двох білінійних функцій є білінійною функцією, а також добуток білінійної функції на дійсне число - білінійна функція, то  - білінійна функція. При цьому  .Тобто,  - симетрична білінійна функція. Далі покладемо  .Тоді  - білінійна функція і  .Тобто, - кососиметрична білінійна функція. Причому .Таким чином, будь-яка білінійна функція є сумою деякої симетричної та деякої кососиметричної білінійних функцій. |