|
|
лабораторнаю. Контрольная работа 9 Обыкновенные дифференциальные уравнения тема обыкновенные дифференциальные уравнения. Дифференциальные уравнения первого порядка
Контрольная работа № 9
Обыкновенные
дифференциальные уравнения
ТЕМА 9. Обыкновенные дифференциальные уравнения.
Дифференциальные уравнения первого порядка.
Дифференциальные уравнения высших порядков.
Системы обыкновенных дифференциальных уравнений с постоянными коэффициентами.
СПИСОК ЛИТЕРАТУРЫ
Демидович Б. П., Моденов В. П. Дифференциальные уравнения: Учебное пособие. - СПб.: Иван Федоров, 2003. - 287 с.
Степанов В. В. Курс дифференциальных уравнений: Учеб. для вузов. - 8-е изд., стер. - М.: Едиториал УРСС, 2004. - 486 с.
Матвеев Н. М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям: Учеб. пособие. - 7-е изд., доп. - СПб.: Лань, 2002. - 431 с.
Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. пособие: в 2-х т.- Изд. стер. –М.: Интеграл – Пресс. Т.1. -2001.- 415 с. Т.2.- 2002.- 544 с.
Решение типового варианта контрольной работы.
Задание 1. Найти общее решение дифференциальных уравнений.
а) 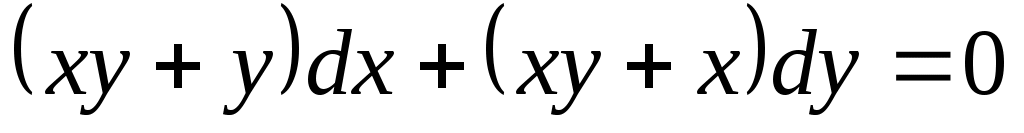 . .
Решение. Попытаемся разделить переменные интегрирования. Для этого вынесем за скобки общий множитель: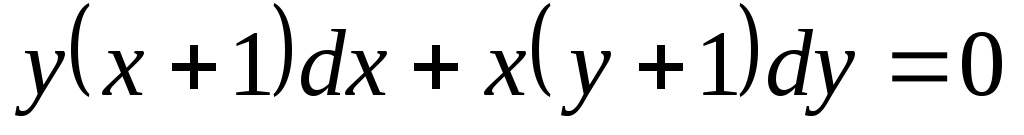 , разнесем слагаемые: , разнесем слагаемые: 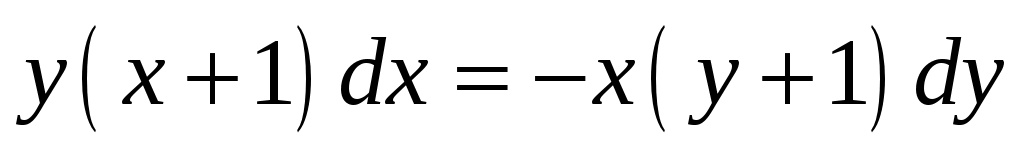 ; выражая ; выражая 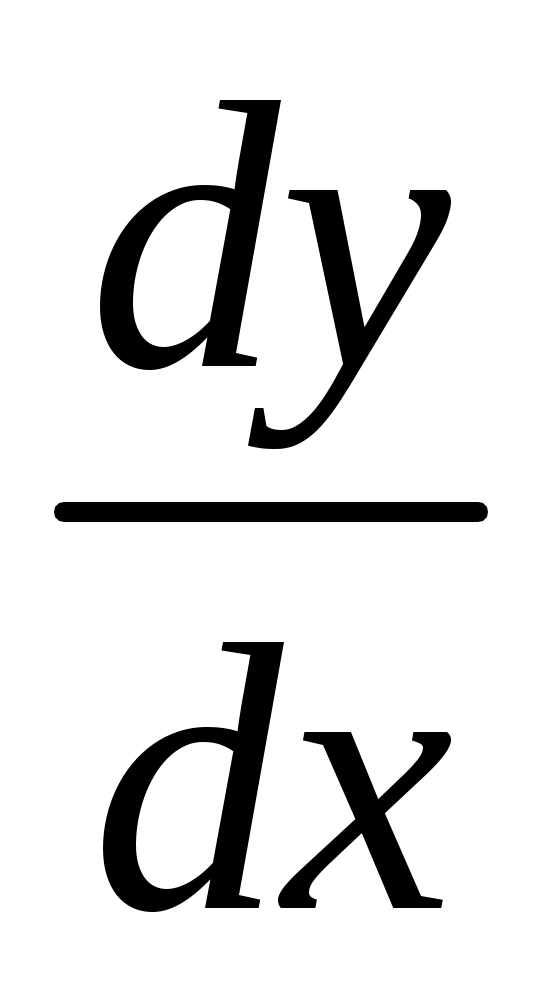 из полученного уравнения убедимся в том, что из полученного уравнения убедимся в том, что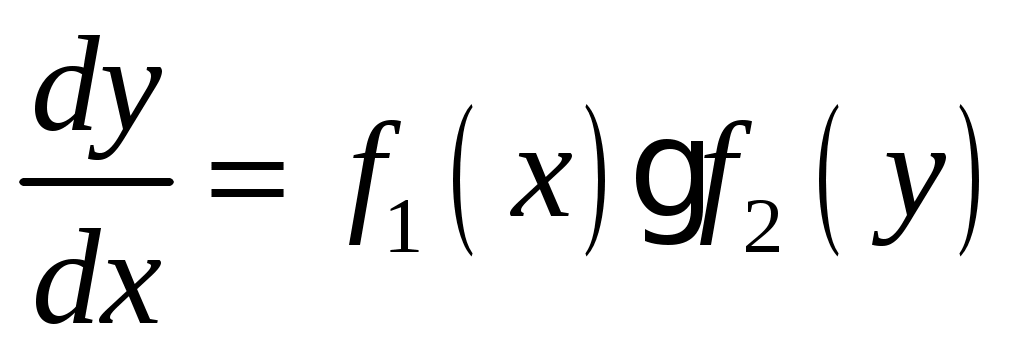 и, значит, наше уравнение является дифференциальным уравнением в разделяющихся переменных. Разделим переменные. и, значит, наше уравнение является дифференциальным уравнением в разделяющихся переменных. Разделим переменные. 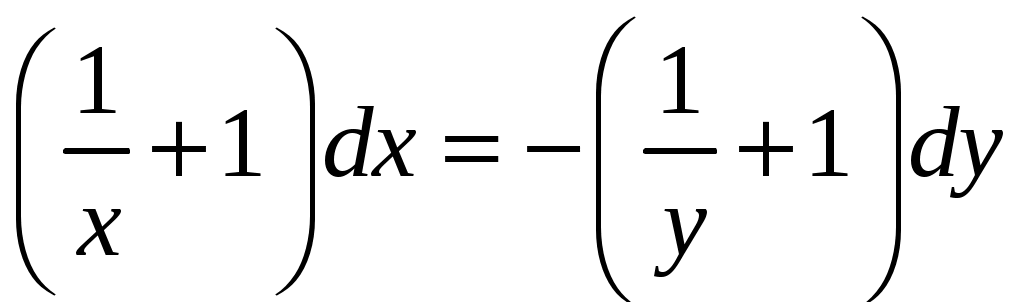 . .
Проинтегрируем получившееся выражение по соответствующим переменным: 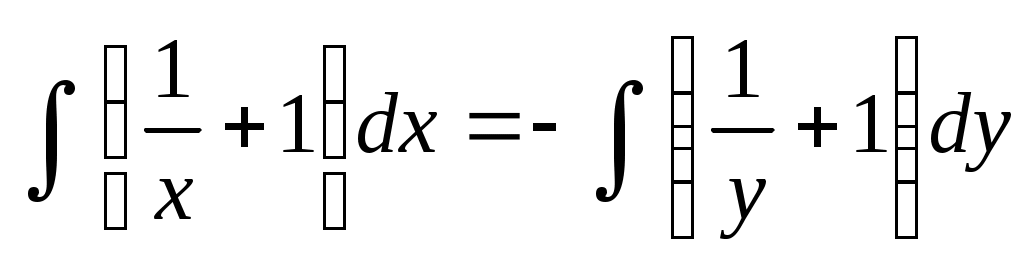 . .
Получим 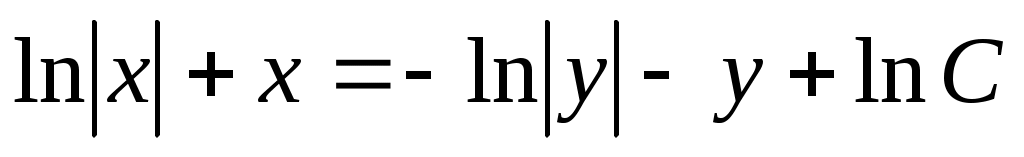 , ,  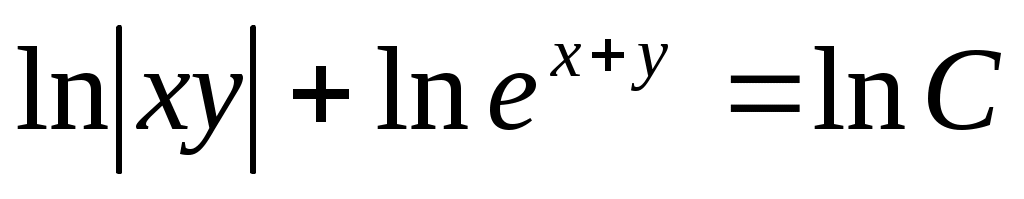 . .
Таким образом, мы убедились в том, что 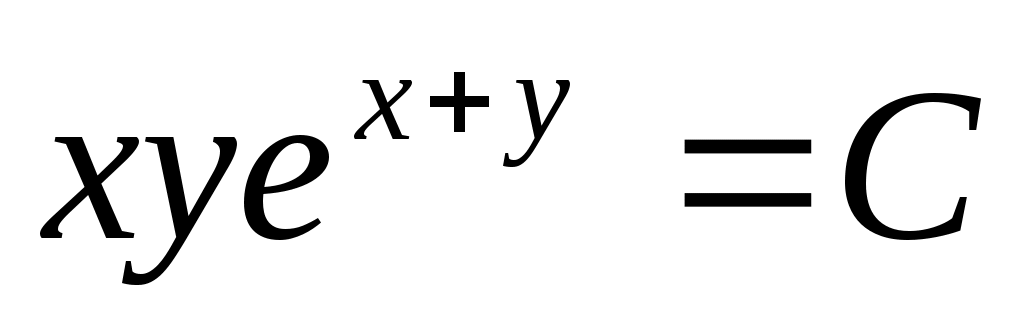 - общий интеграл заданного уравнения. - общий интеграл заданного уравнения.
Ответ: 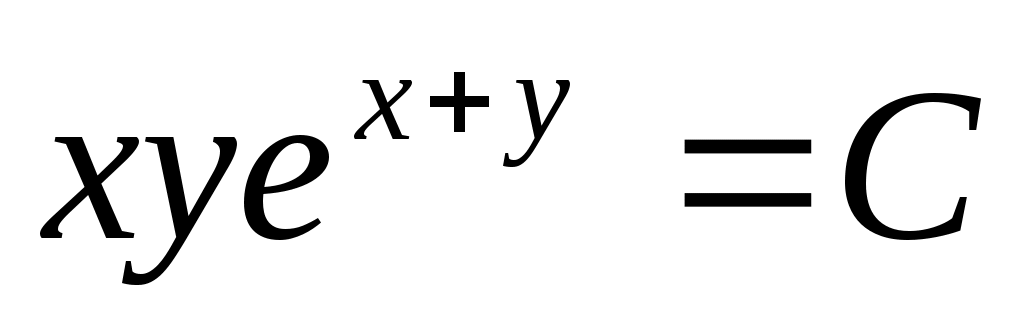 . .
б)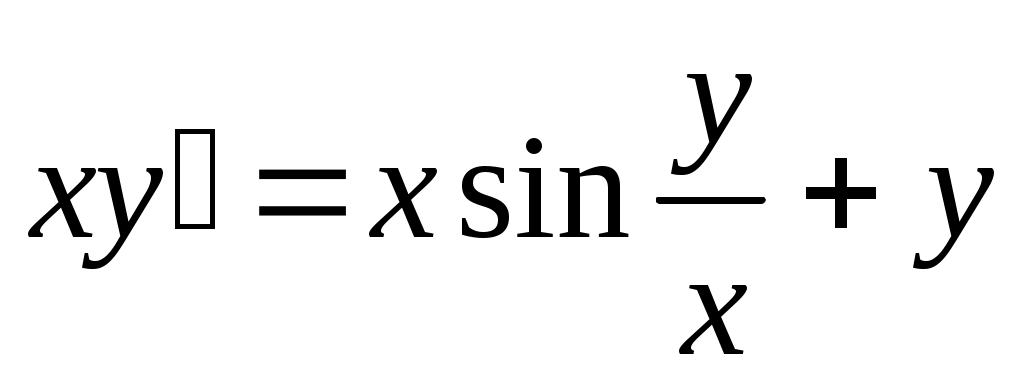 . .
Решение. Убедимся в том, что переменные разделить не удается. Поэтому поделим обе части уравнения на x.
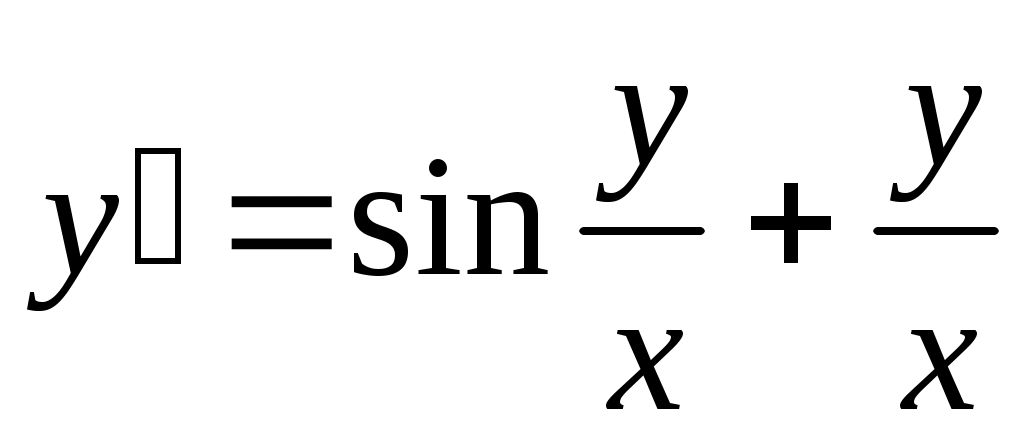 - Убедимся в том, что производная - Убедимся в том, что производная 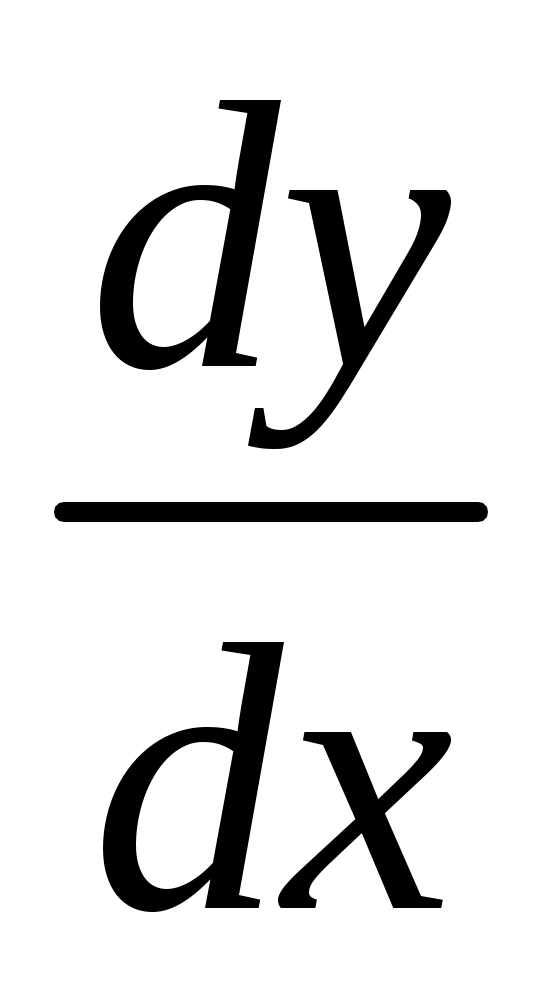 в представленном уравнении зависит только от отношения в представленном уравнении зависит только от отношения 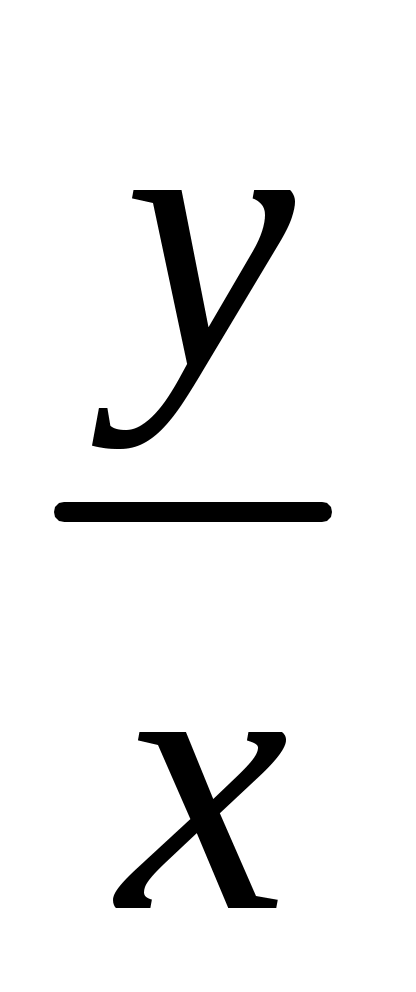 , то есть , то есть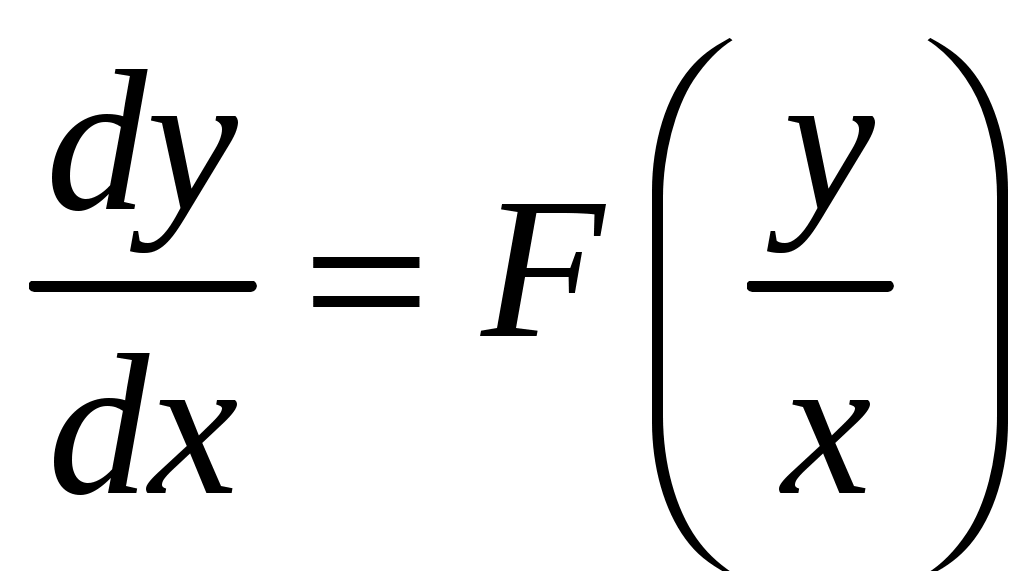 и, значит, это однородное дифференциальное уравнение 1-го порядка. Будем решать его с помощью соответствующей замены. и, значит, это однородное дифференциальное уравнение 1-го порядка. Будем решать его с помощью соответствующей замены.
Введем новую переменную 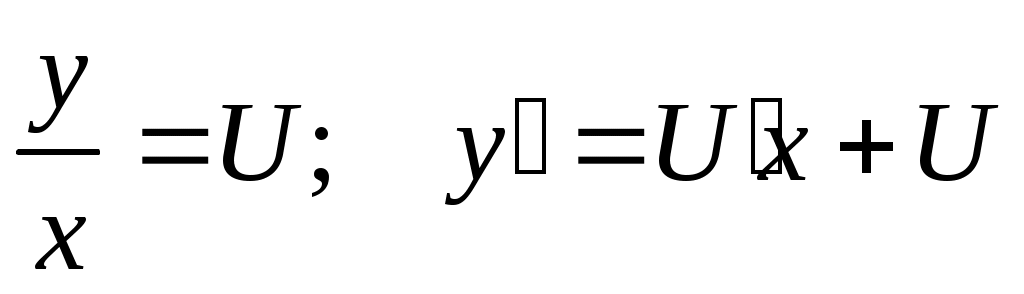 . .
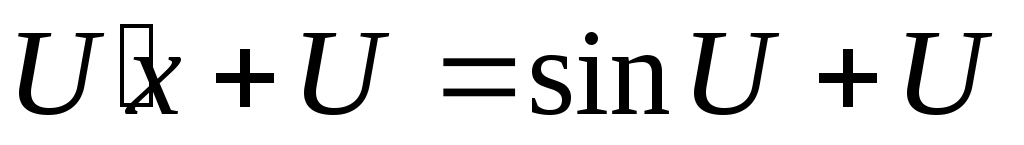 ; ;
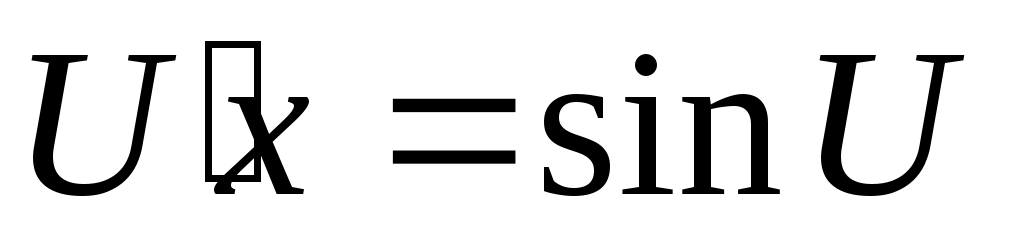 ; ;
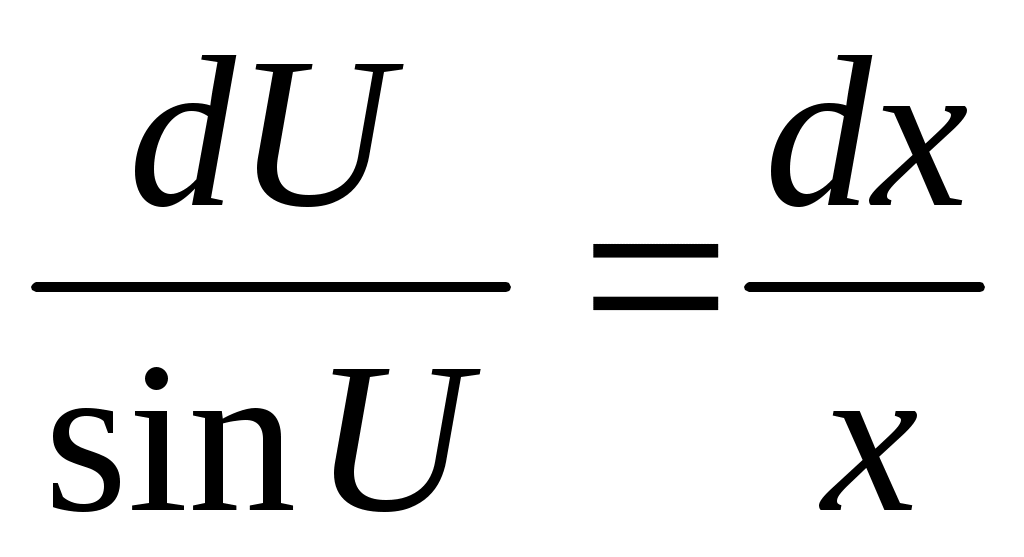 ; проинтегрируем выражение ; проинтегрируем выражение
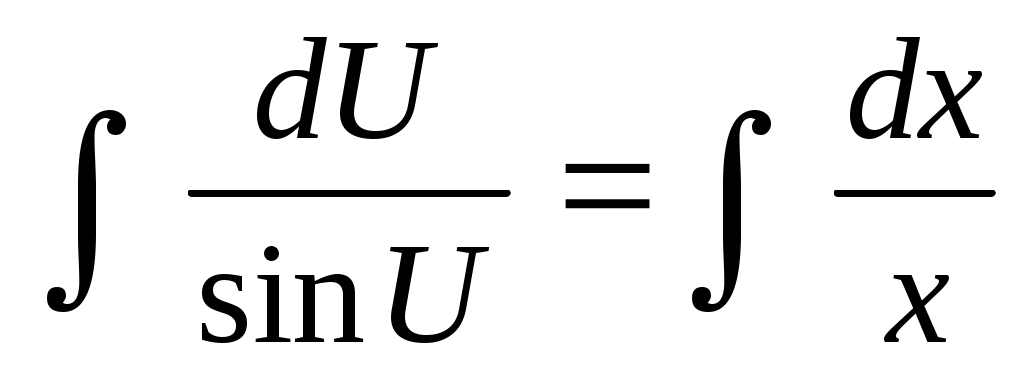 ; ;
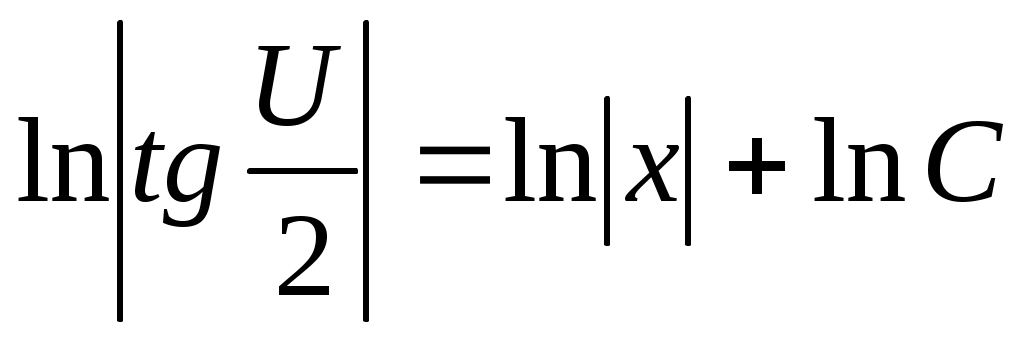 ; ;
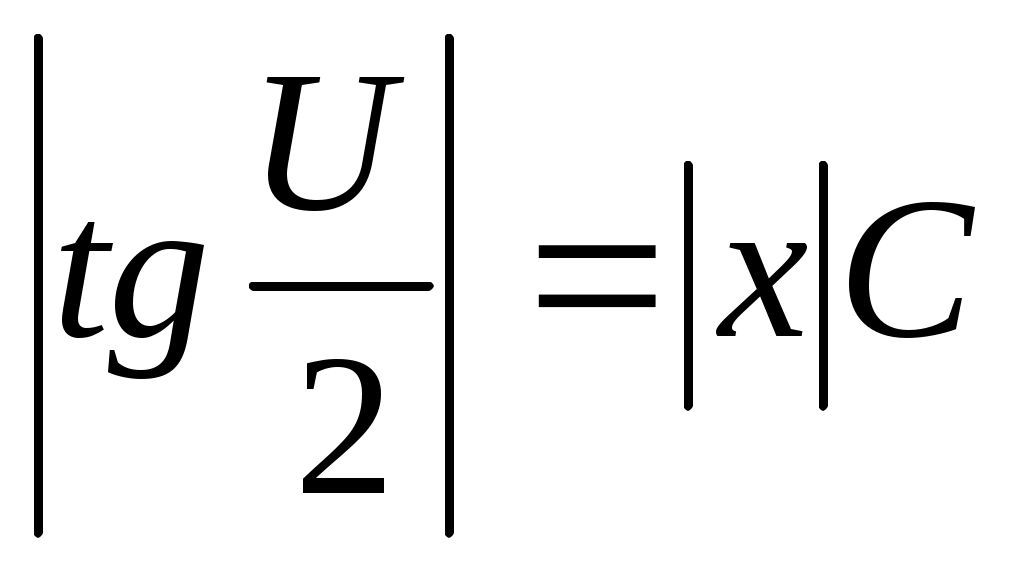 ; ;
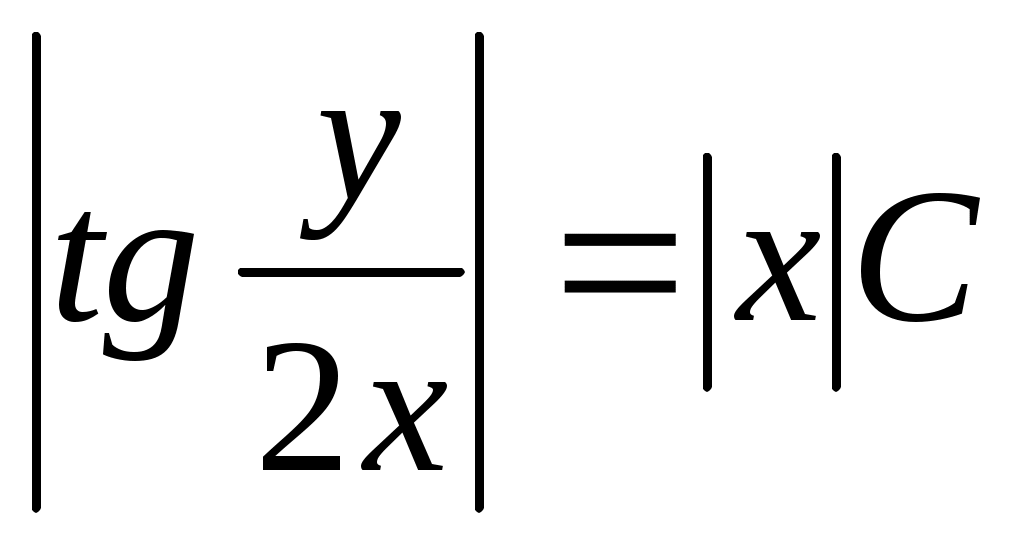 ; ;
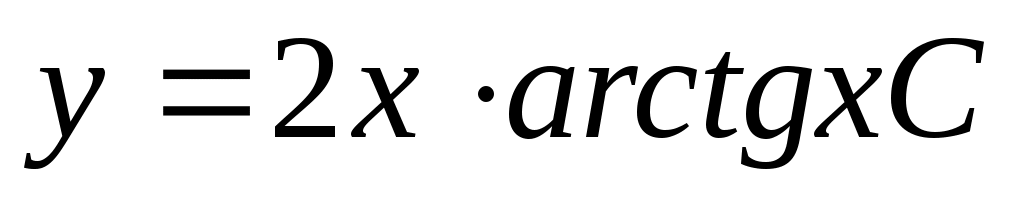 - общее решение уравнения. - общее решение уравнения.
Ответ: 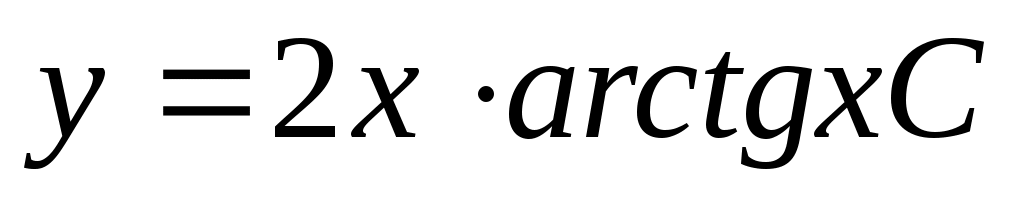 . .
в)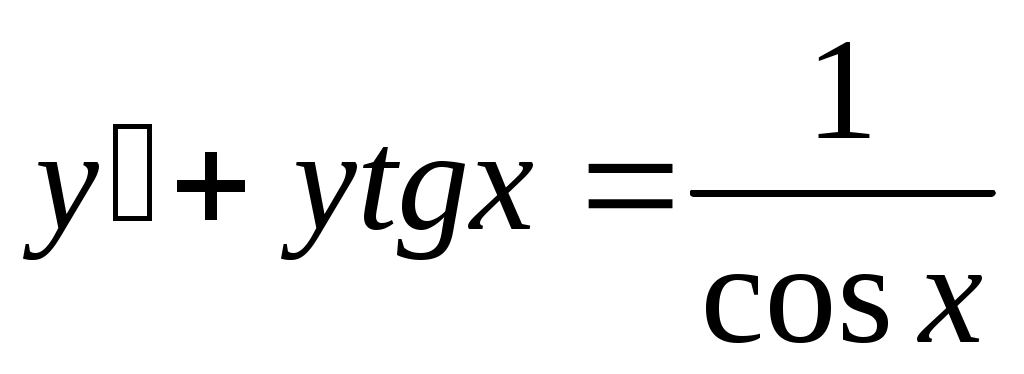 . .
Решение. Начинаем вновь с проверки не разделятся ли переменные интегрирования. Убеждаемся, что это не так, и, кроме того, однородным оно тоже не является. Это линейное дифференциальное уравнение 1-го порядка, так как имеет структуру вида: 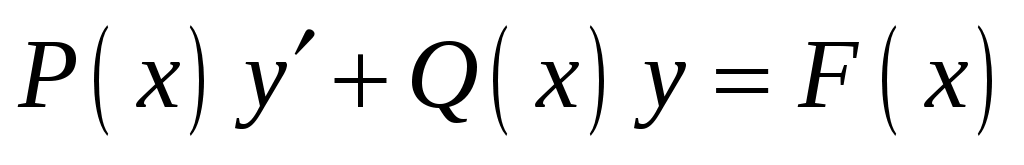 . Будем решать его с помощью стандартной в этом случае, замены: . Будем решать его с помощью стандартной в этом случае, замены: 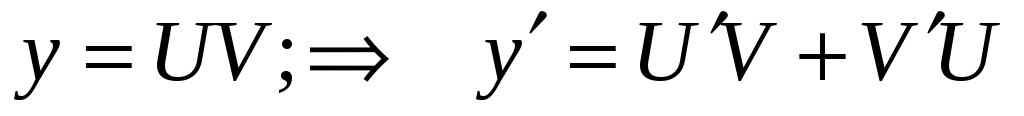 . .
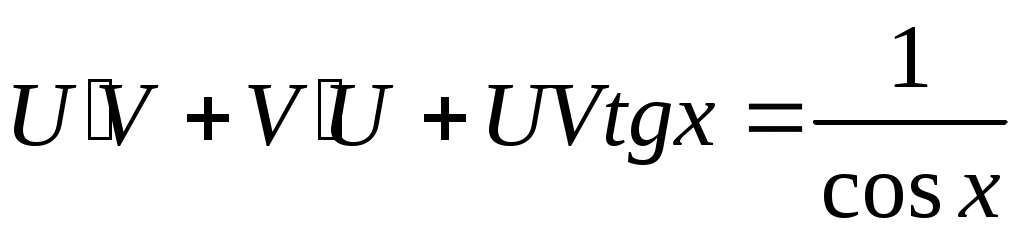 ; ;
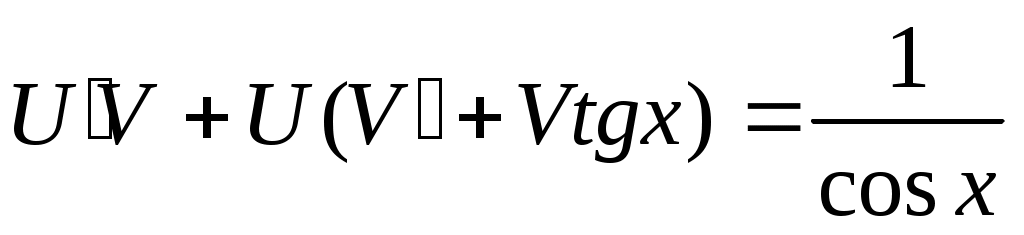 ; ;
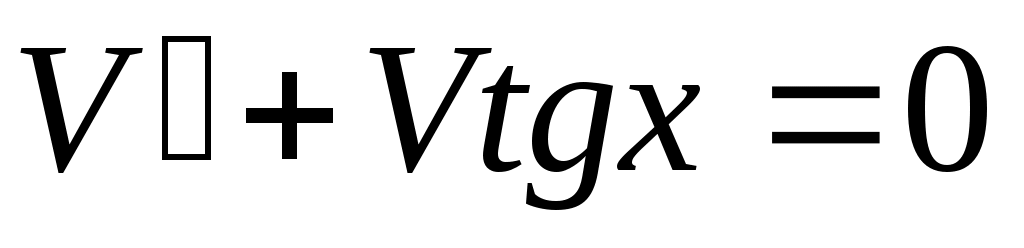 ; ;
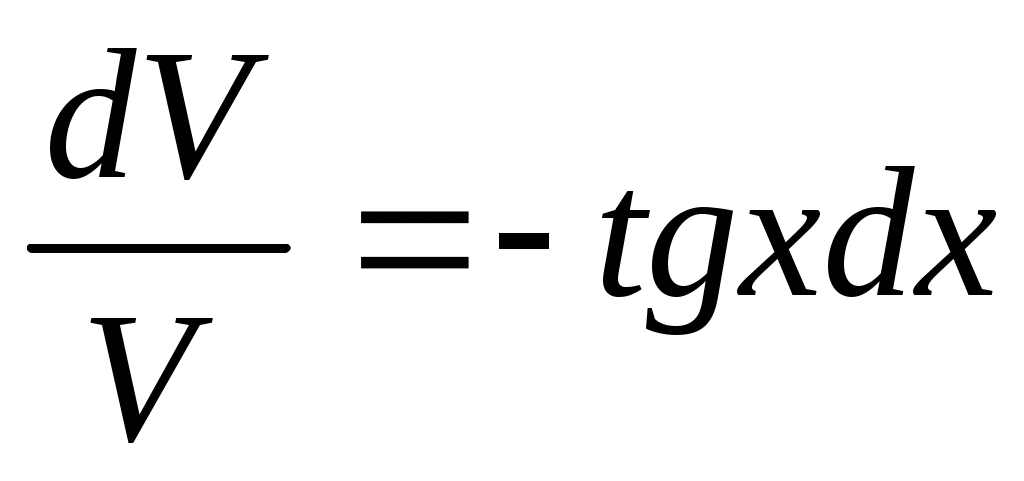 ; ;
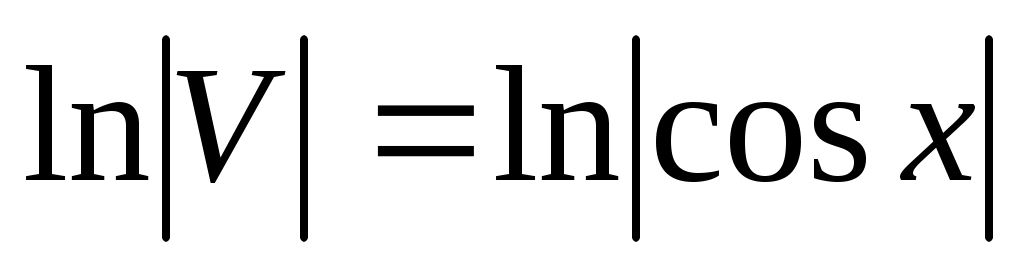 ; ;
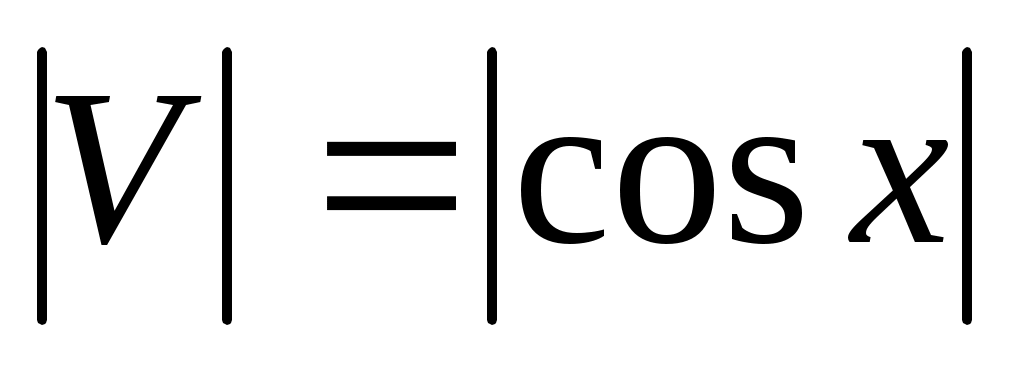 ; ;
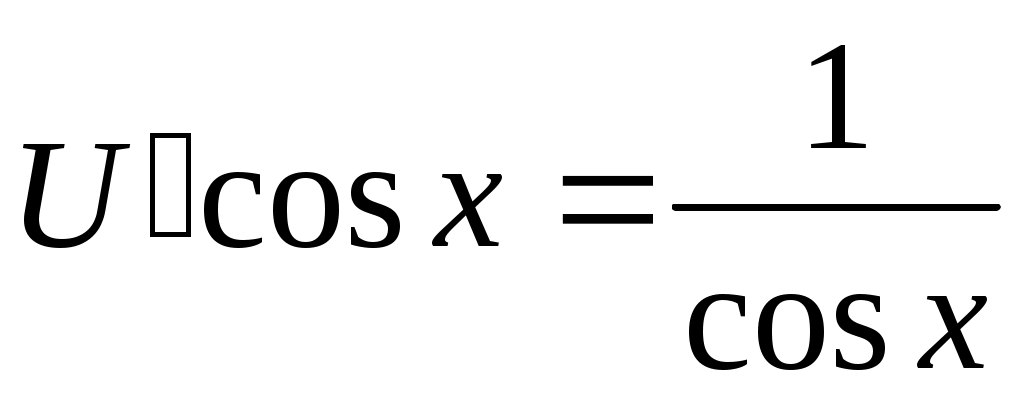 ; ;
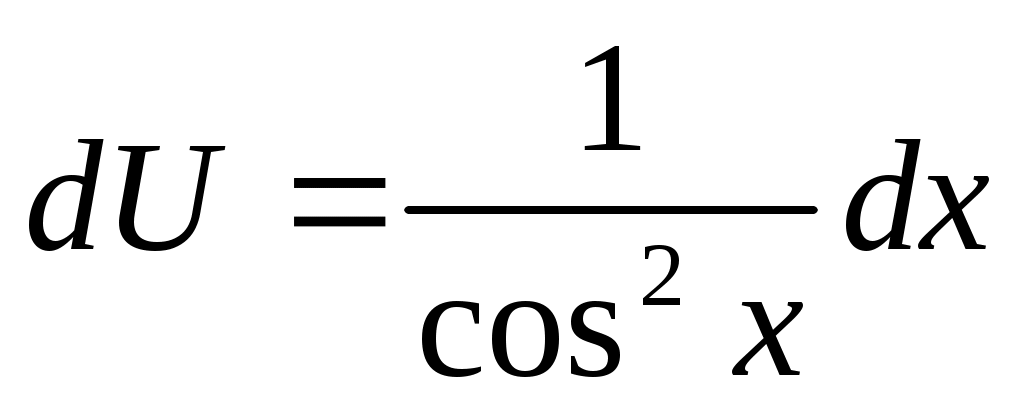 ; ;
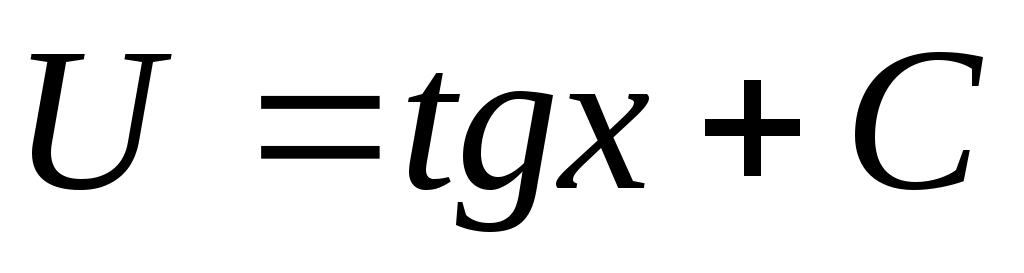 ; ;
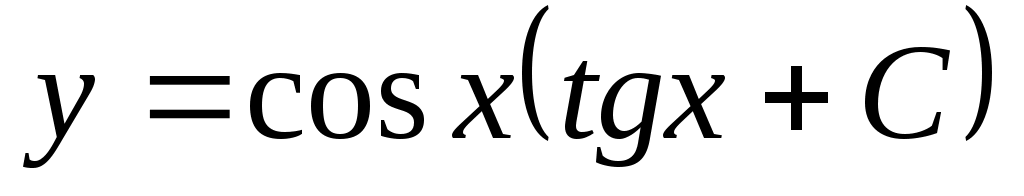 - общее решение уравнения. - общее решение уравнения.
Ответ: 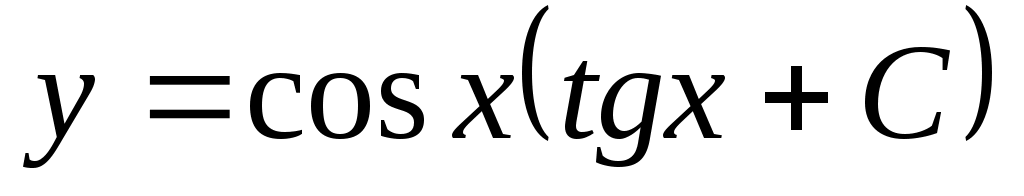 . .
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям 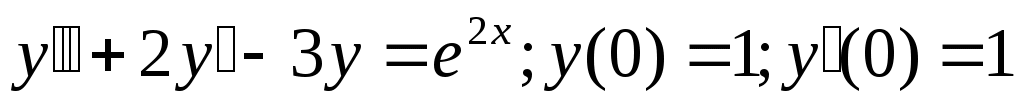 . .
Решение. 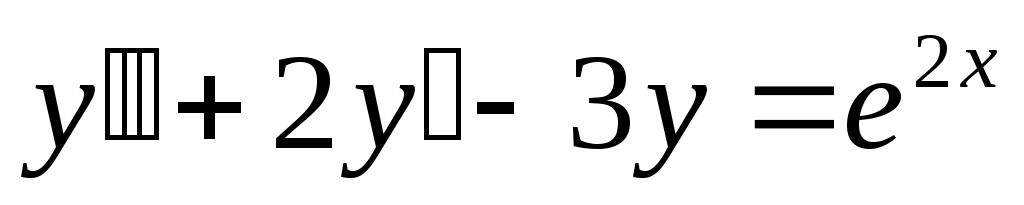 - неоднородное линейное дифференциальное уравнение с постоянными коэффициентами 2-ого порядка. Решение будем искать в виде суммы решений: общего решения однородного уравнения - неоднородное линейное дифференциальное уравнение с постоянными коэффициентами 2-ого порядка. Решение будем искать в виде суммы решений: общего решения однородного уравнения 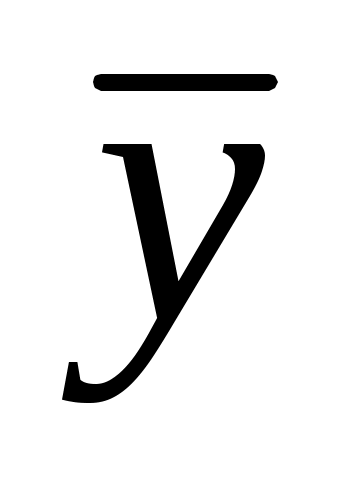 и частного решения неоднородного уравнения и частного решения неоднородного уравнения 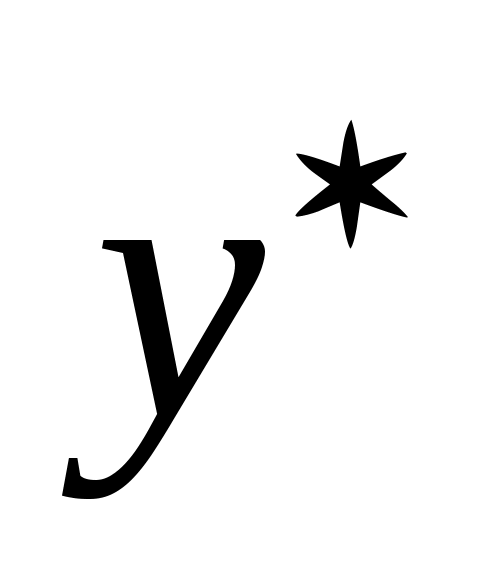 , которое будем искать по виду правой части. Начнем с отыскания , которое будем искать по виду правой части. Начнем с отыскания 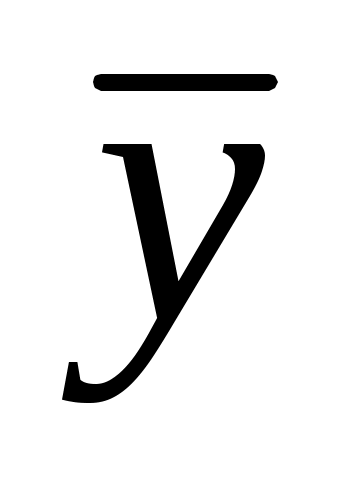 . .
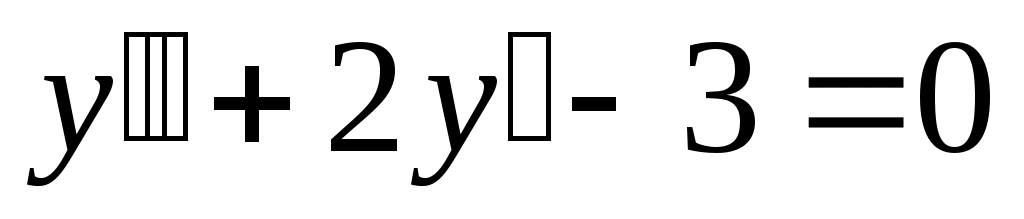 Составим характеристическое уравнение: Составим характеристическое уравнение: 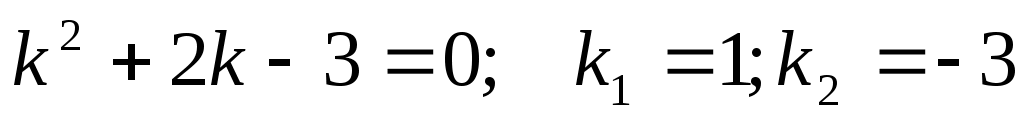 . .
Следовательно, общее решение однородного уравнения: 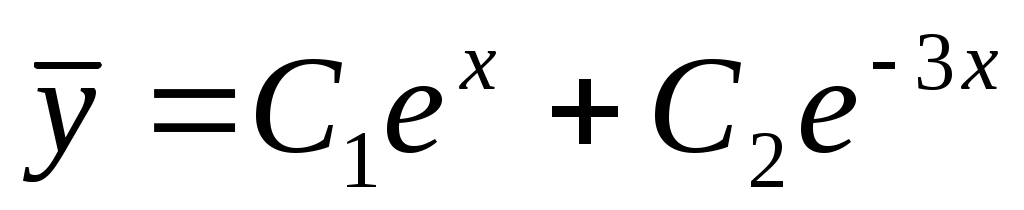 . .
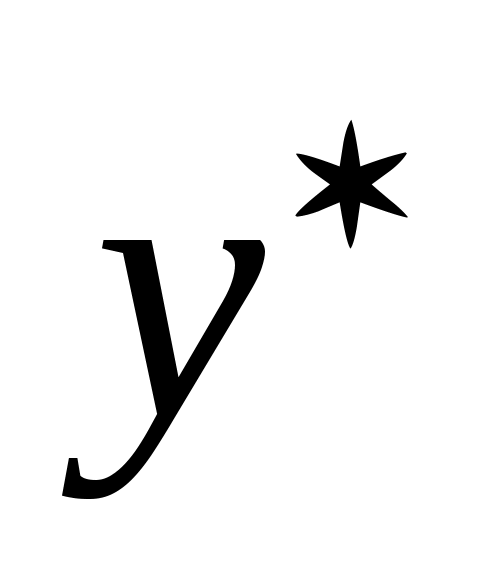 будем искать в виде будем искать в виде 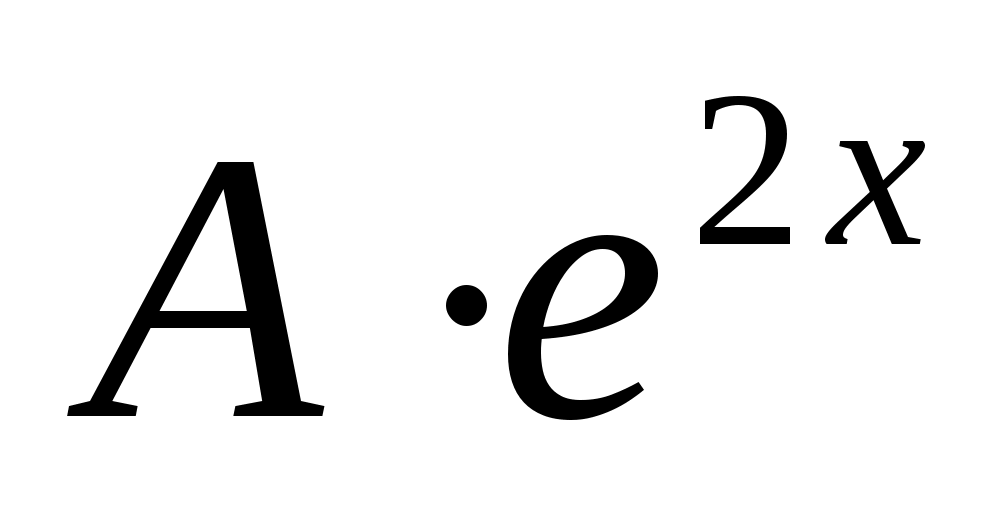 . . 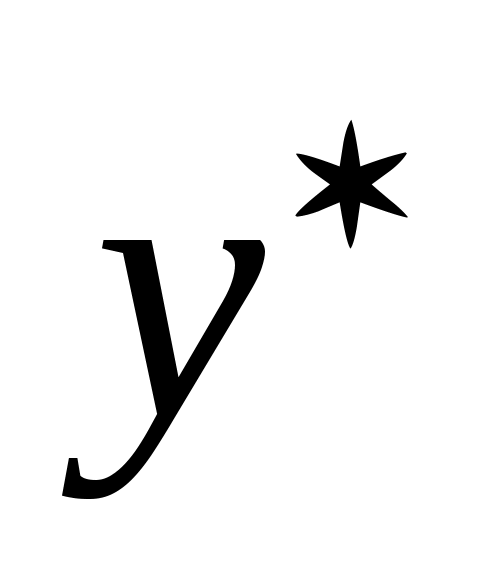 - частное решение уравнения, поэтому оно превращает его в верное числовое тождество. Подставим его в уравнение и вычислим А. - частное решение уравнения, поэтому оно превращает его в верное числовое тождество. Подставим его в уравнение и вычислим А. 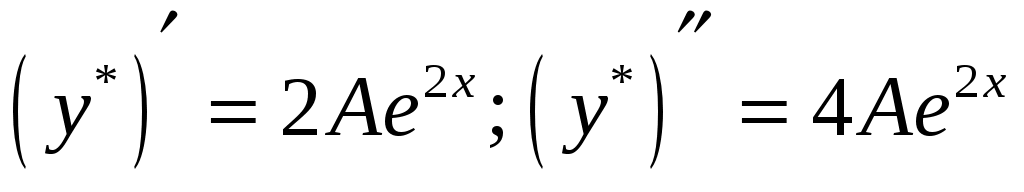 . .
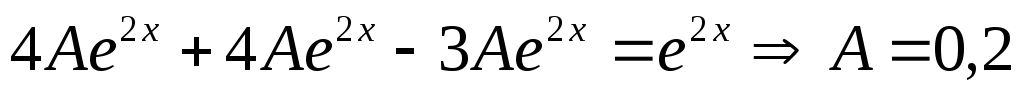 . Значит . Значит 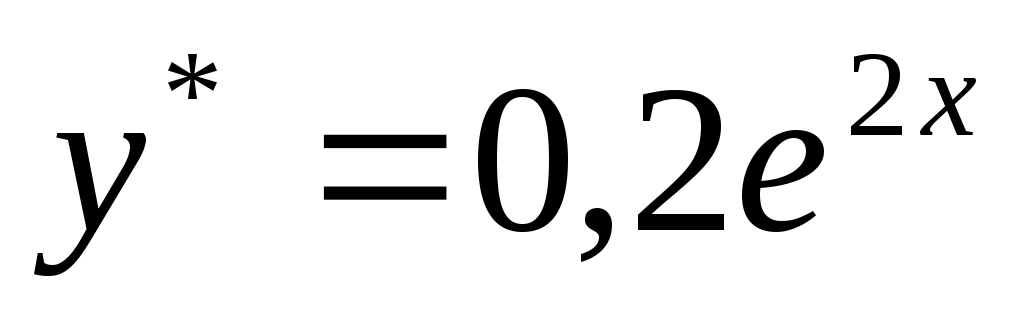 . Таким образом, общее решение неоднородного уравнения . Таким образом, общее решение неоднородного уравнения 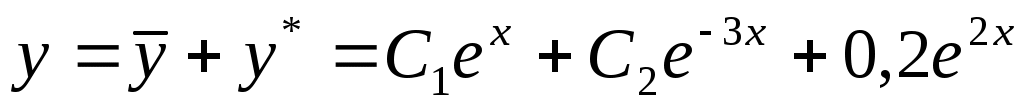 . Для вычисления частного решения определим значения констант исходя из начальных условий: . Для вычисления частного решения определим значения констант исходя из начальных условий:
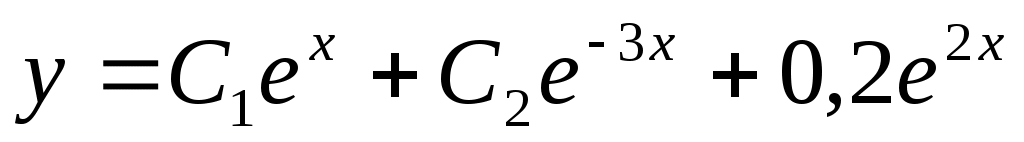 ; ; 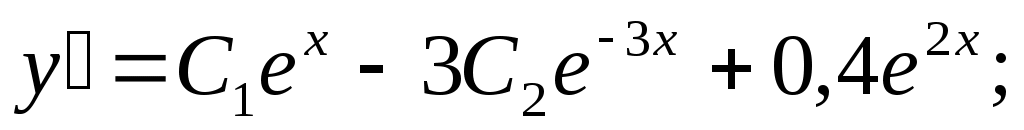 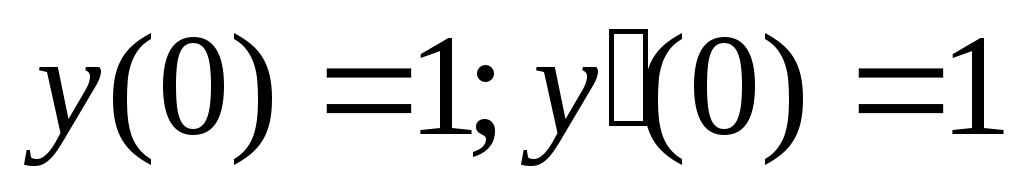 ; ;
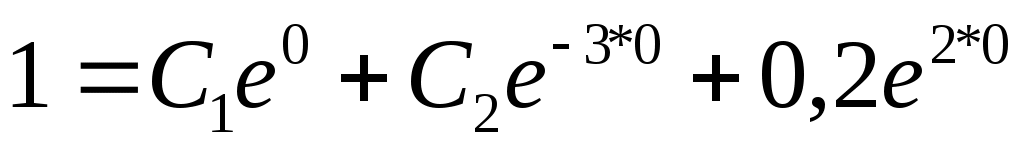 ; ; 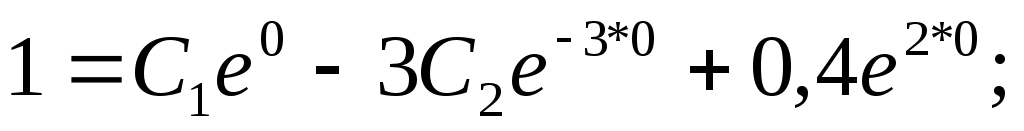
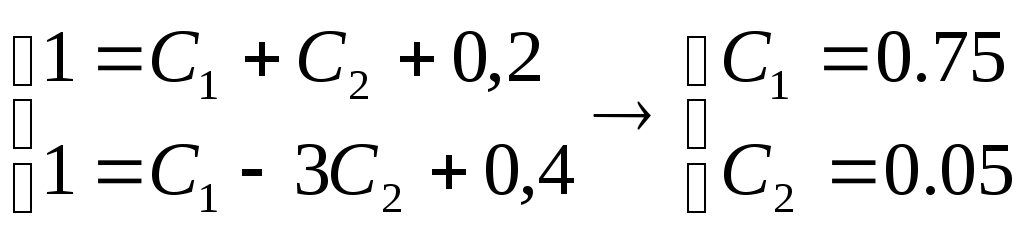
Ответ: 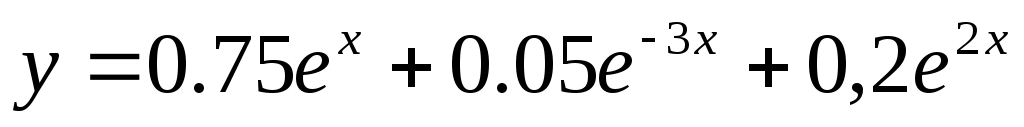 . .
Задание 3. Найти общее решение системы дифференциальных уравнений 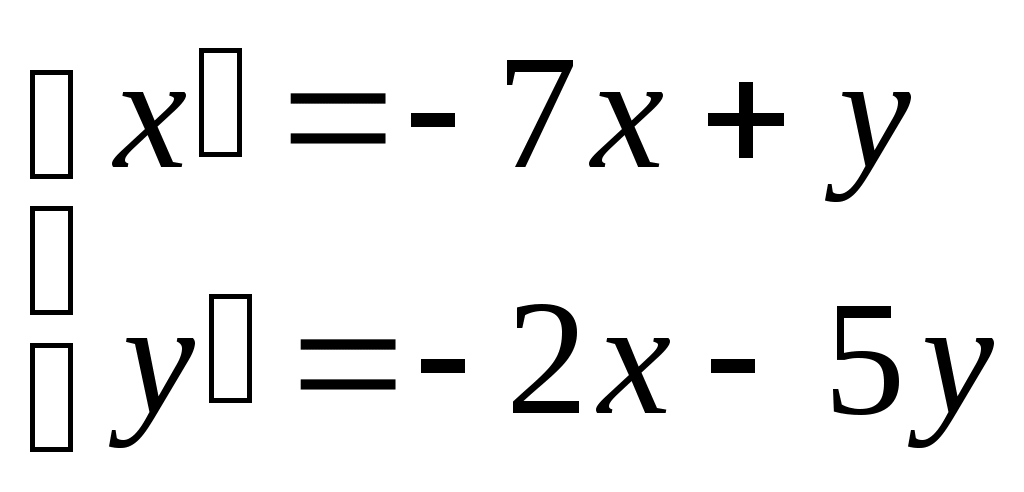 . .
Решение. Сведем предложенную систему к одному дифференциальному уравнению с постоянными коэффициентами второго порядка. Для этого продифференцируем первое уравнение системы по t:
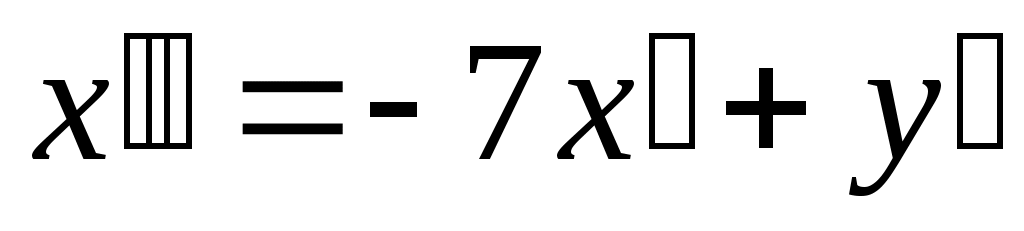 и заменим и заменим  воспользовавшись для этого вторым уравнением системы: воспользовавшись для этого вторым уравнением системы:
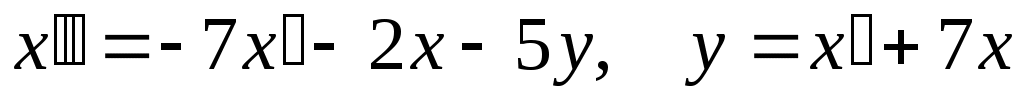 . Окончательно . Окончательно 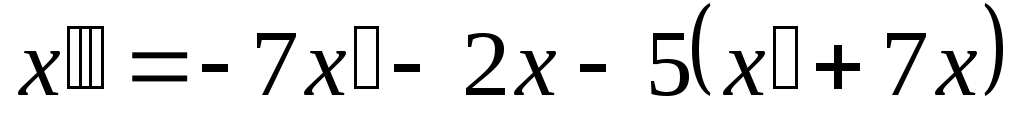 . .
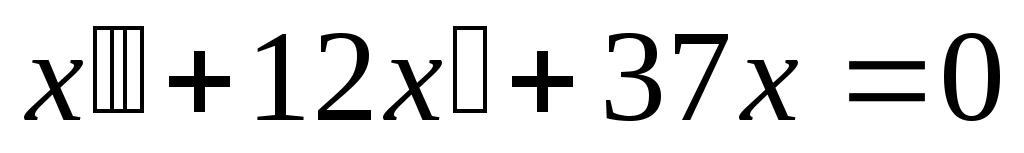 - однородное линейное дифференциальное уравнение с постоянными коэффициентами. Составим характеристическое уравнение: - однородное линейное дифференциальное уравнение с постоянными коэффициентами. Составим характеристическое уравнение: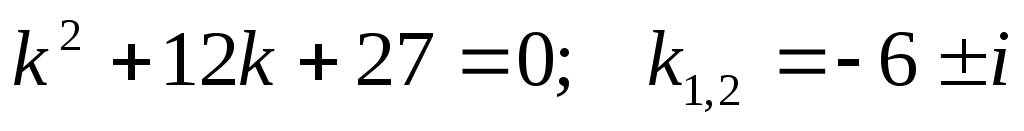 . .
Следовательно, решение: 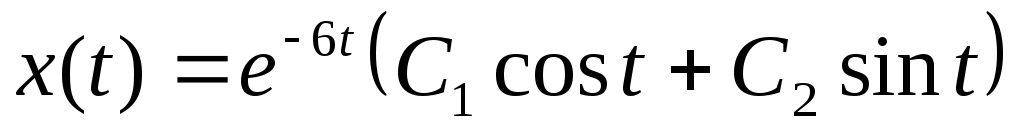 . Из первого уравнения . Из первого уравнения 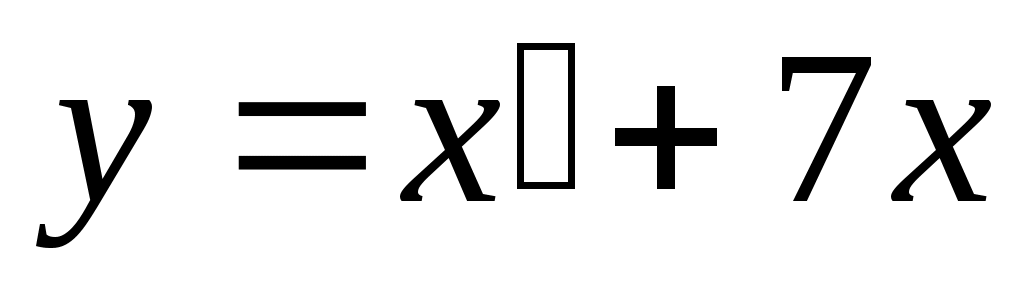 , поэтому , поэтому 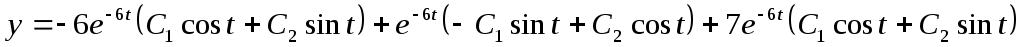 ; ;
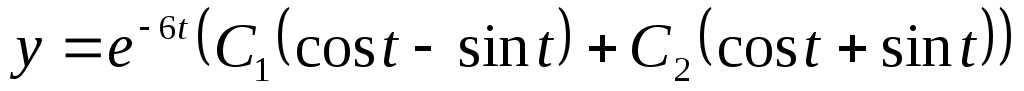 . .
Ответ: 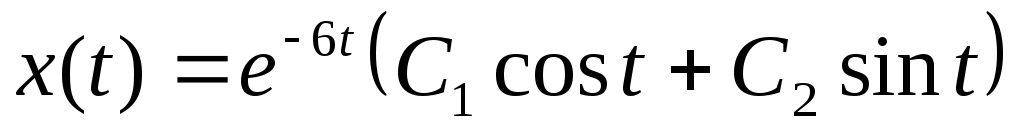 ; ; 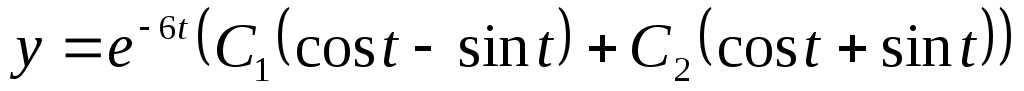 . .
Задание 4. Записать уравнение кривой, проходящей через точку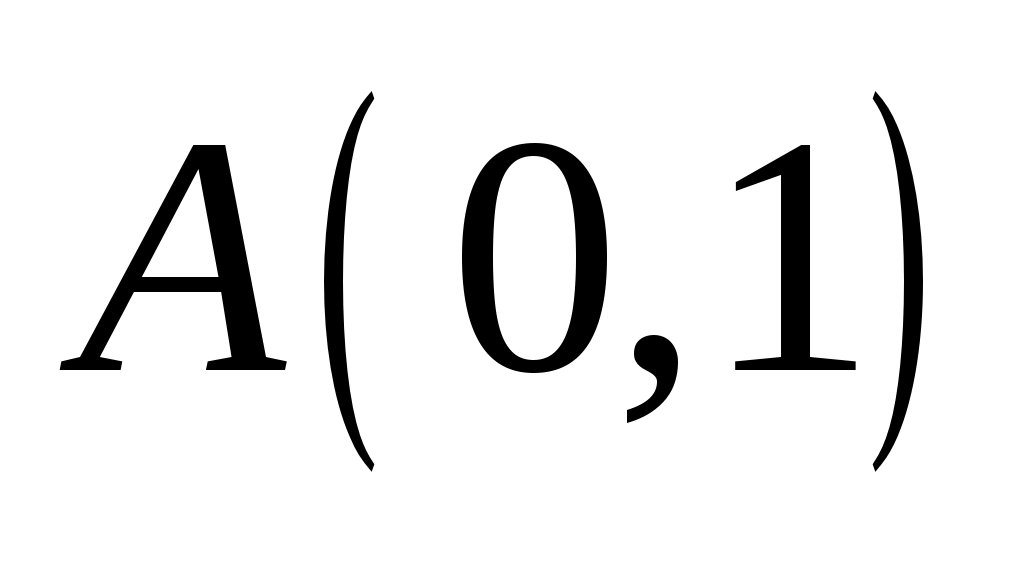 , для которой треугольник, образованный осью Оу, касательной к кривой в произвольной её точке и радиус-вектором точки касания, равнобедренный (причем основанием его служит отрезок касательной от точки касания до оси Оу). , для которой треугольник, образованный осью Оу, касательной к кривой в произвольной её точке и радиус-вектором точки касания, равнобедренный (причем основанием его служит отрезок касательной от точки касания до оси Оу).
Решение. Пусть 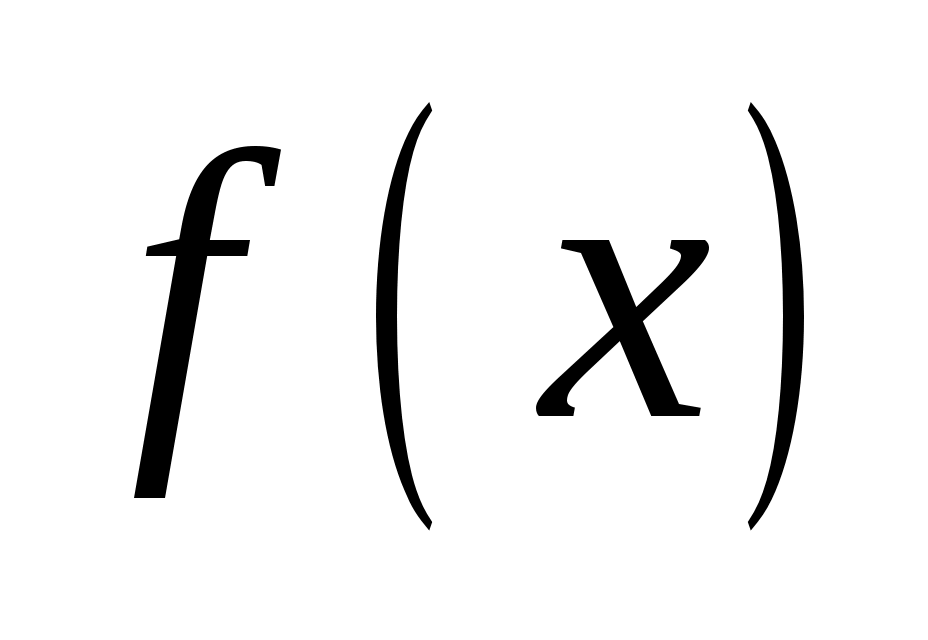 искомое уравнение кривой. Проведем касательную MNв произвольной точке M(x;y) кривой до пересечения с осью Оу в точкеN. Согласно условию, должно выполняться равенство искомое уравнение кривой. Проведем касательную MNв произвольной точке M(x;y) кривой до пересечения с осью Оу в точкеN. Согласно условию, должно выполняться равенство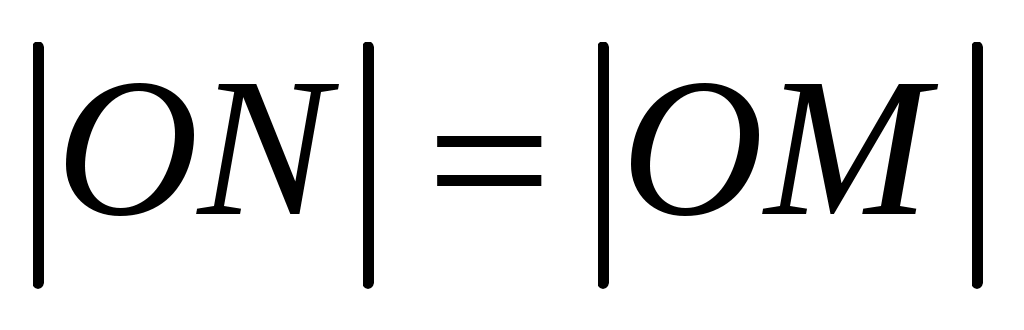 , но , но 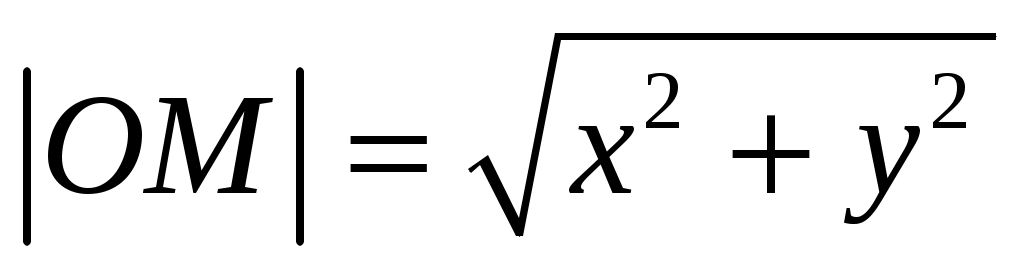 , а , а  найдем из уравнения найдем из уравнения 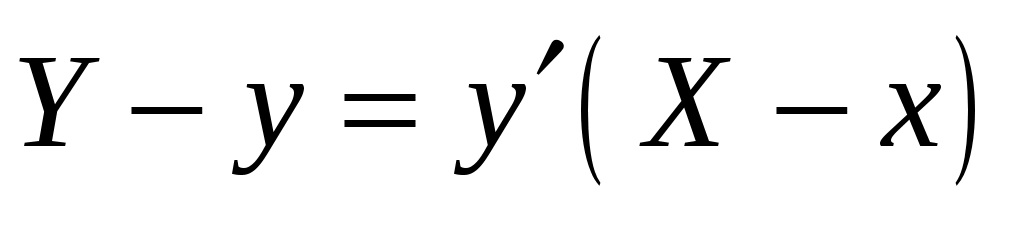 , полагая X=0, то есть , полагая X=0, то есть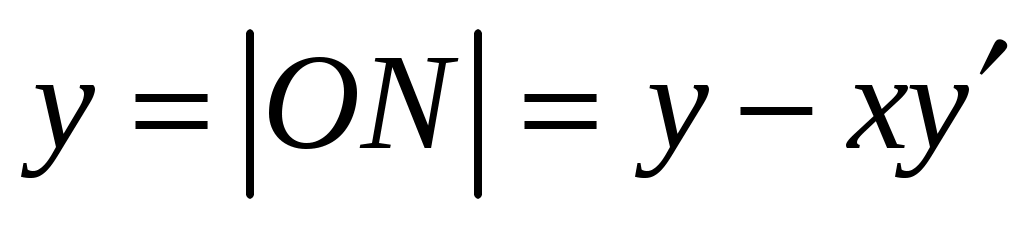 . .
Итак, приходим к однородному уравнению 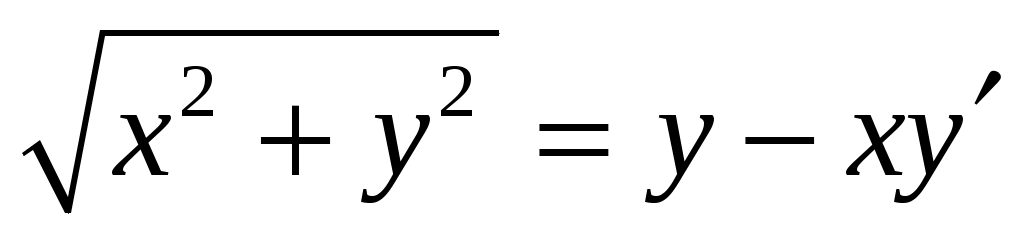 . .
Полагая y=tx (y’=t’x+t), получим 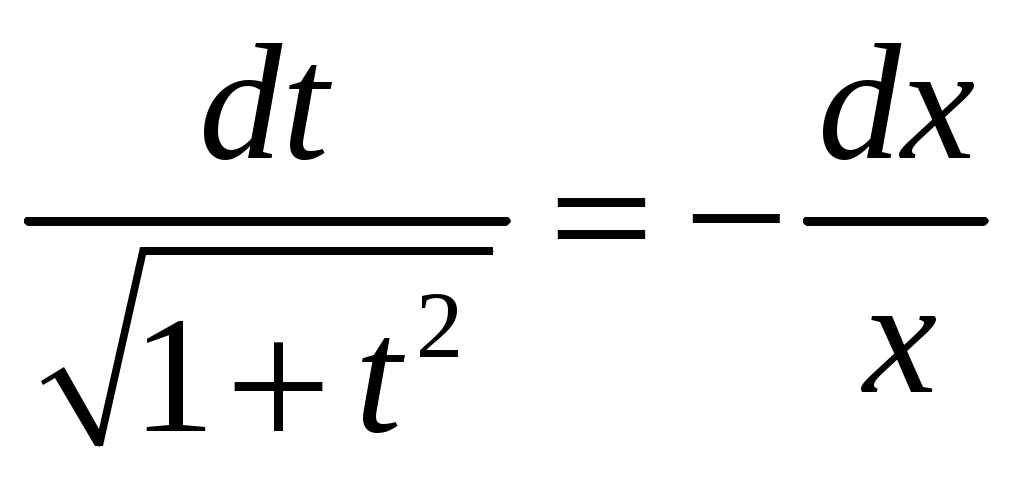 или или 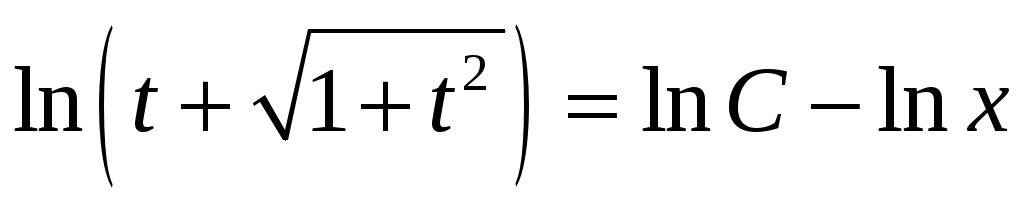 , откуда , откуда 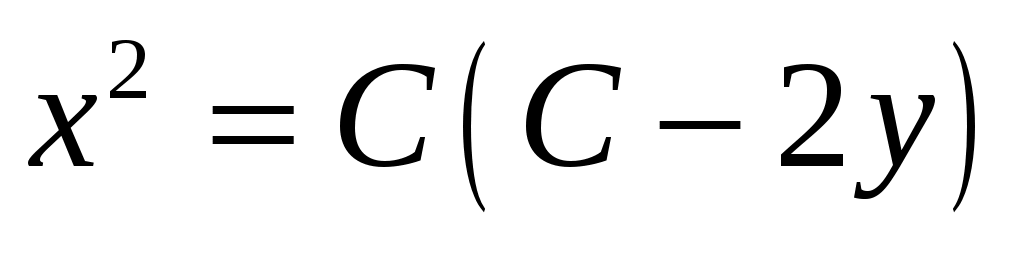 – данное решение представляет собой семейство парабол, осью которых является ось Оу. – данное решение представляет собой семейство парабол, осью которых является ось Оу.
Определим значение константы С исходя из того, что кривая проходит через точку 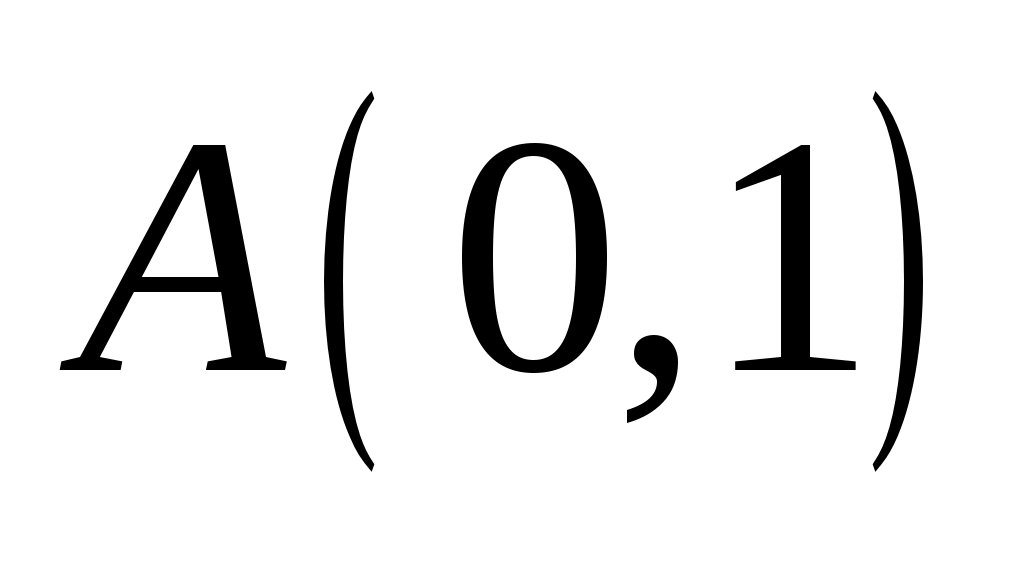 . Подставляя координаты заданной точки в вышенайденное общее решение, получим . Подставляя координаты заданной точки в вышенайденное общее решение, получим 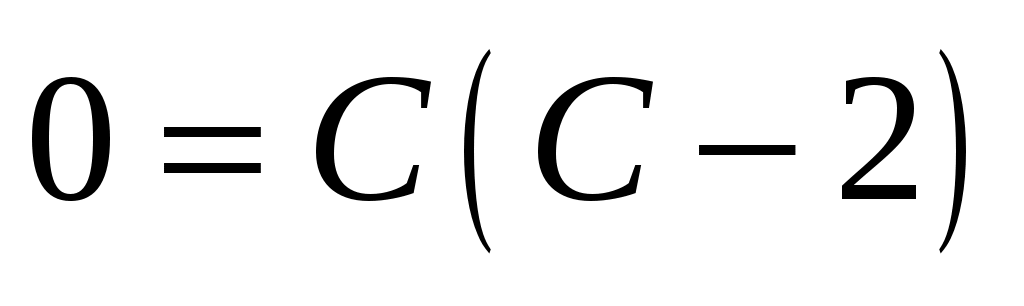 ; из двух значений С=0 и С=2 нас устраивает лишь второе, так как при С=0 парабола оказывается вырожденной. Итак, искомое решение ; из двух значений С=0 и С=2 нас устраивает лишь второе, так как при С=0 парабола оказывается вырожденной. Итак, искомое решение 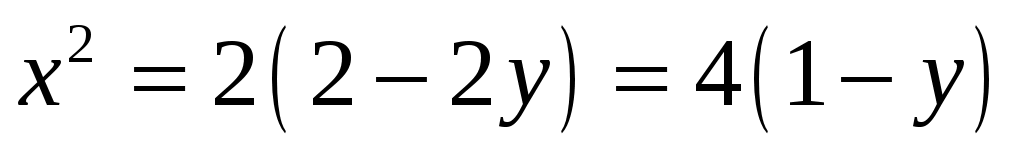 , или , или 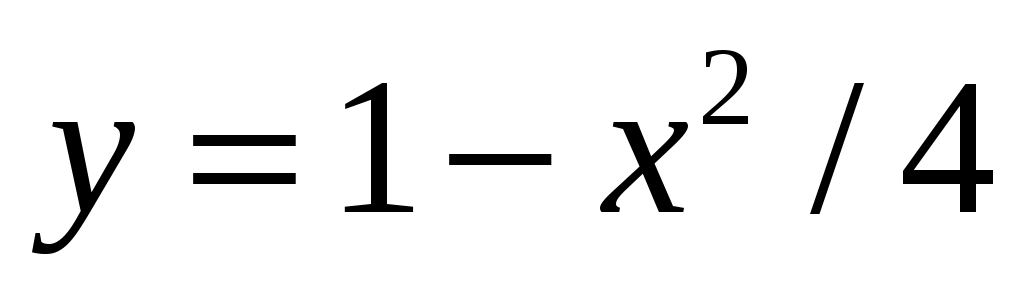 . .
Ответ: 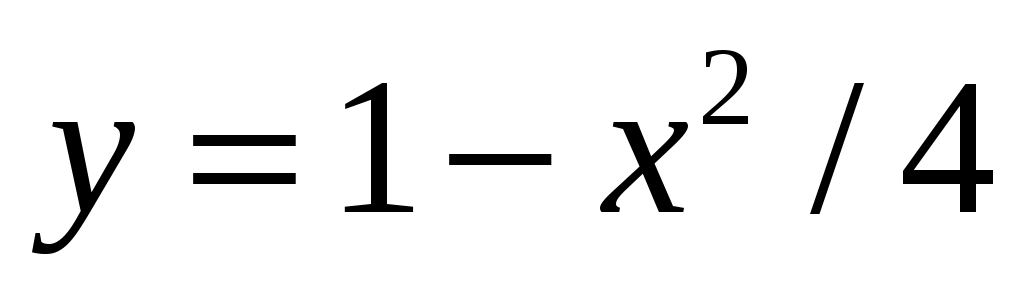 . .
Задание 5.
а) Найти общее решение дифференциального уравнения 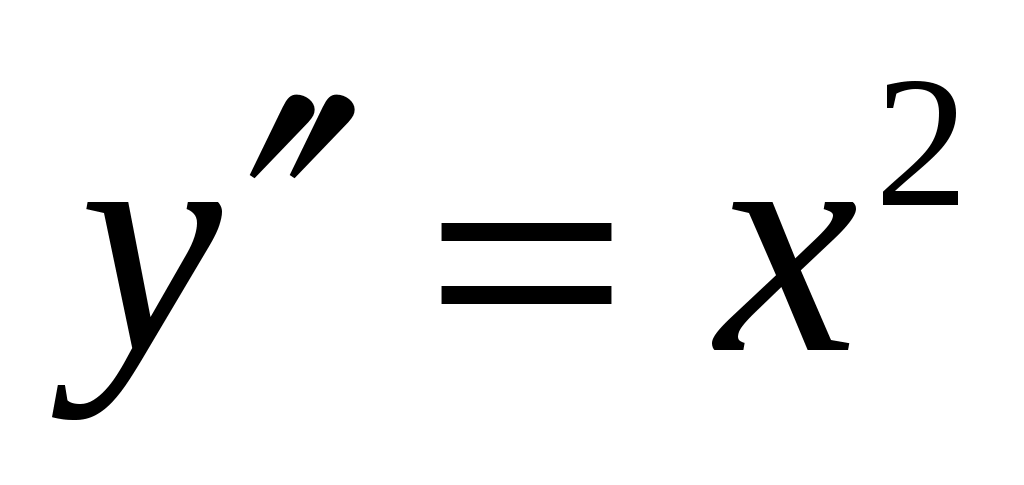 . .
Решение. Так как производная в данном случае является функцией, зависящей только от переменной x, то его решение может быть получено в результате последовательного интегрирования: 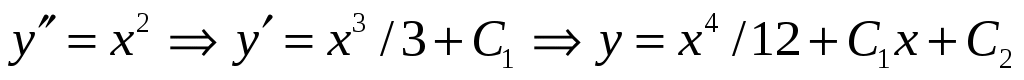 . .
Ответ. 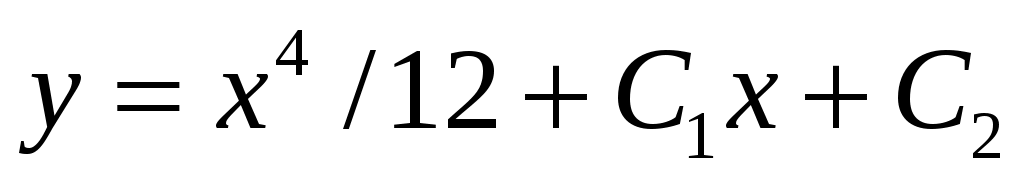 . .
б) Найти общее решение дифференциального уравнения 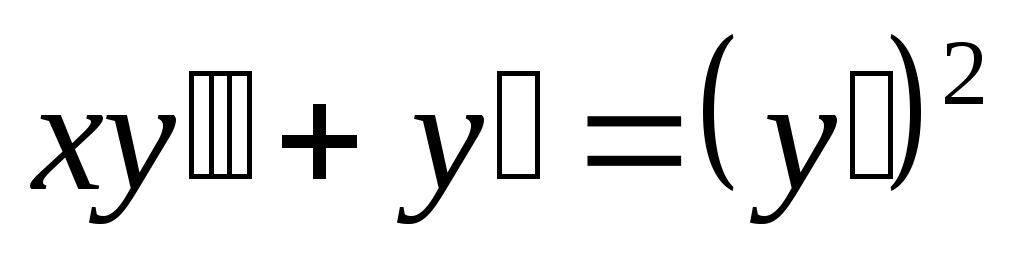 . .
Решение. Поскольку данное уравнение не содержит в явном виде переменной 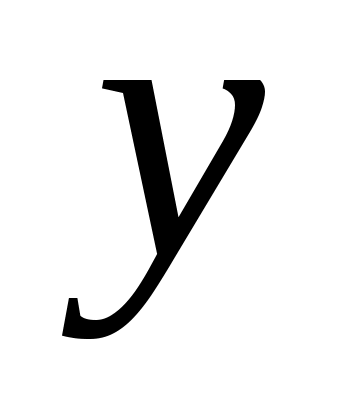 , то замена , то замена 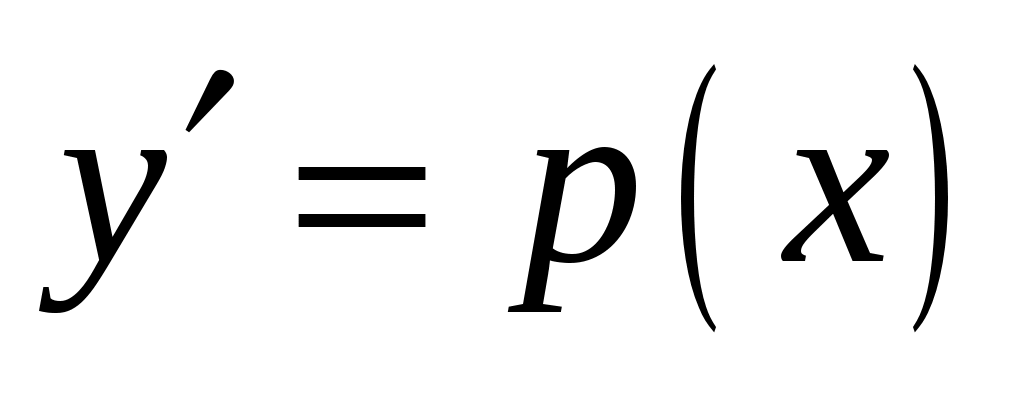 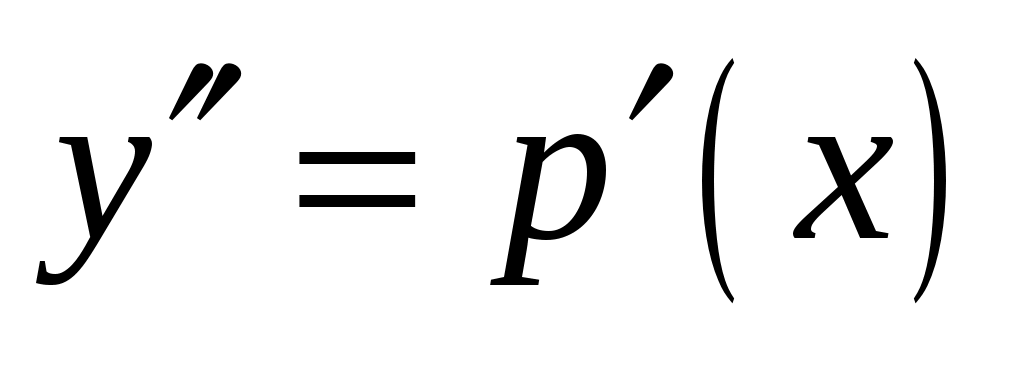 позволяет преобразовать его в уравнение первого порядка с разделяющимися переменными позволяет преобразовать его в уравнение первого порядка с разделяющимися переменными 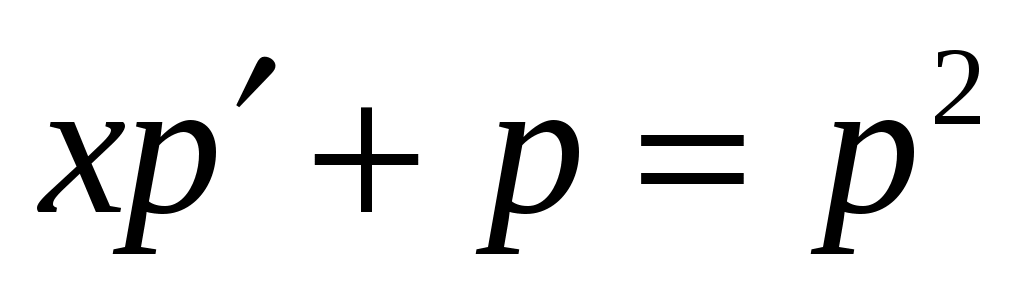 . .
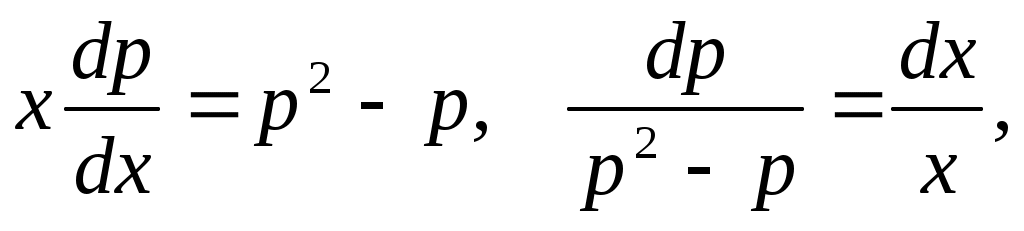
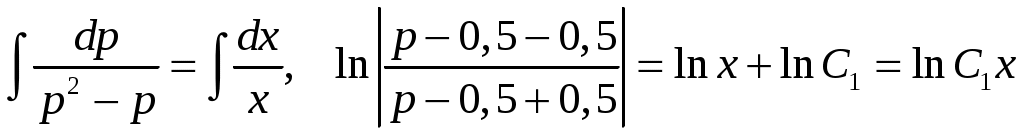 ; ;
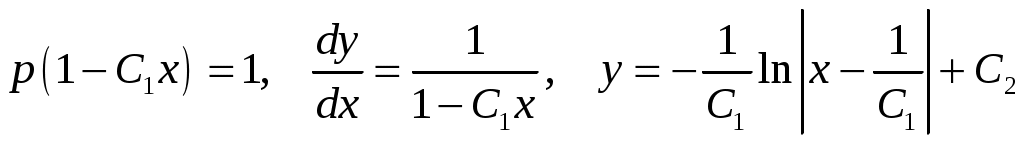 . Учтя, что . Учтя, что  – произвольная постоянная, то полученное решение можно упростить: – произвольная постоянная, то полученное решение можно упростить: 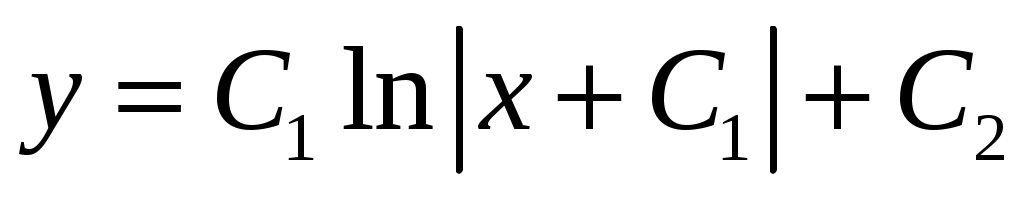 . .
Ответ. 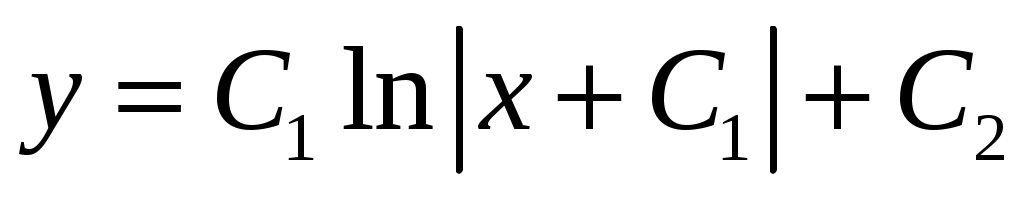 . .
в) Найти общее решение дифференциального уравнения 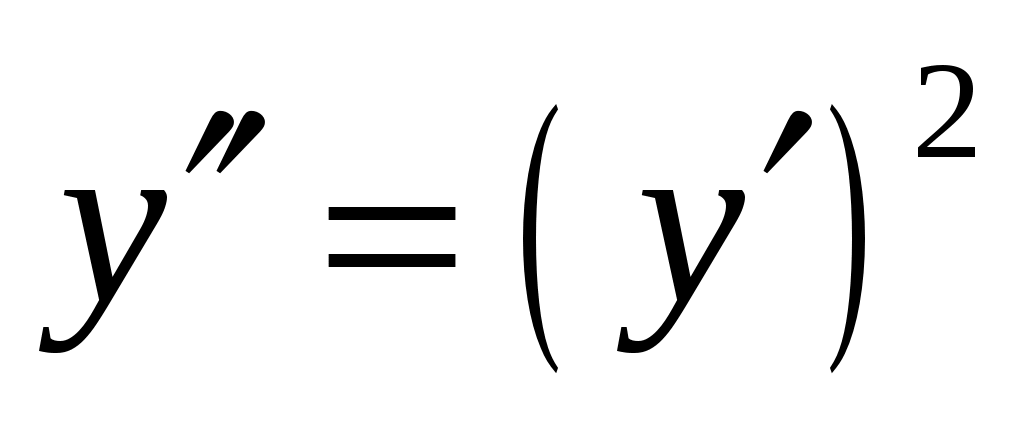 . .
Решение. Так как решаемое уравнение не содержит явно переменной 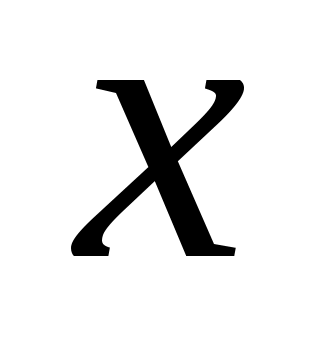 , будем получать его решение с помощью введения новой переменной , будем получать его решение с помощью введения новой переменной 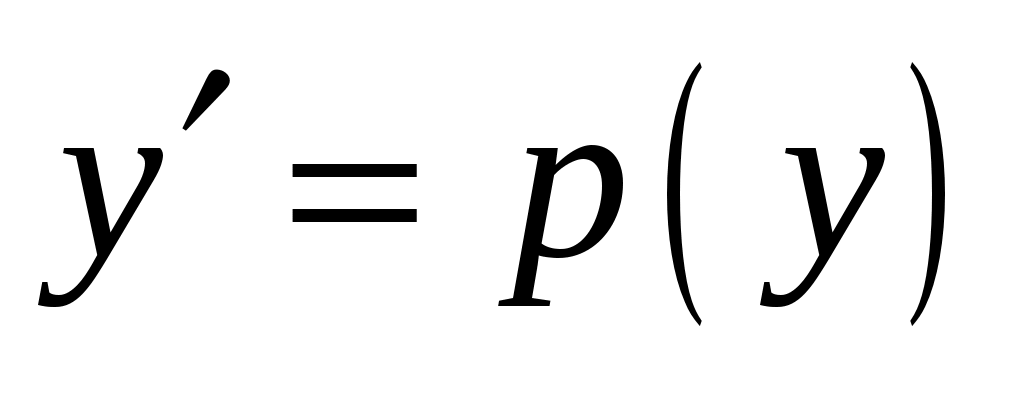 , откуда , откуда 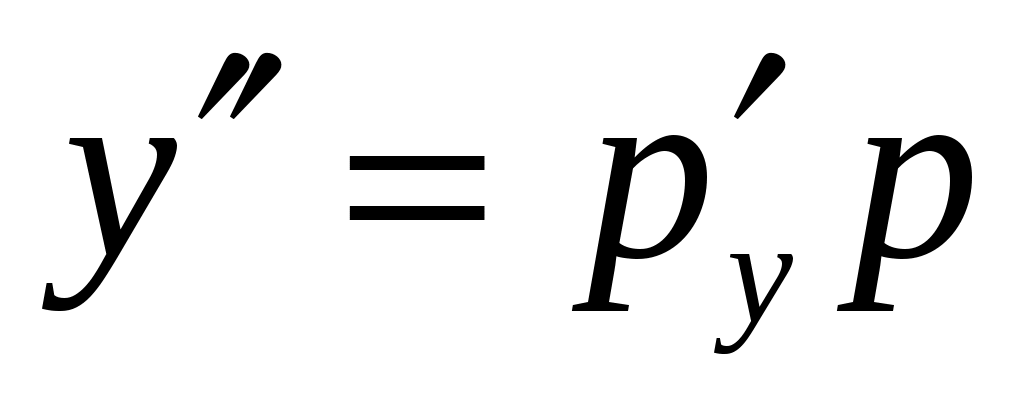 , так как в этом случае мы вычисляем производную сложной функции. Заданное уравнение в результате такой замены будет иметь вид: , так как в этом случае мы вычисляем производную сложной функции. Заданное уравнение в результате такой замены будет иметь вид: 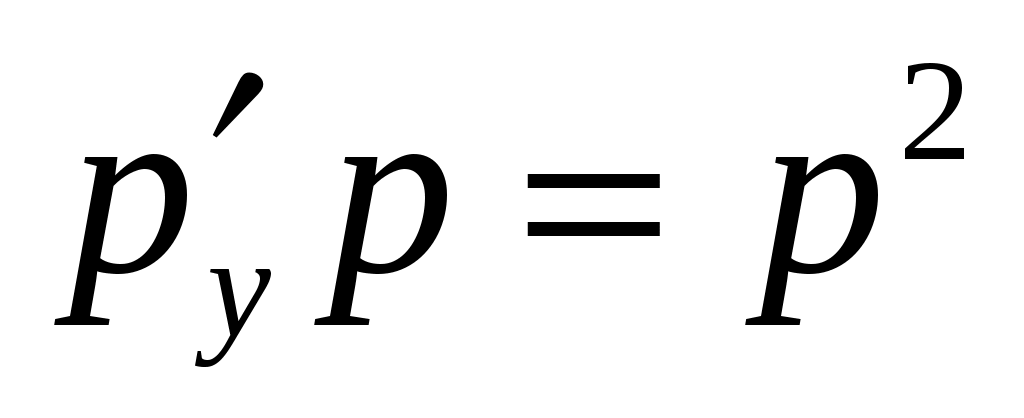 . Решение . Решение 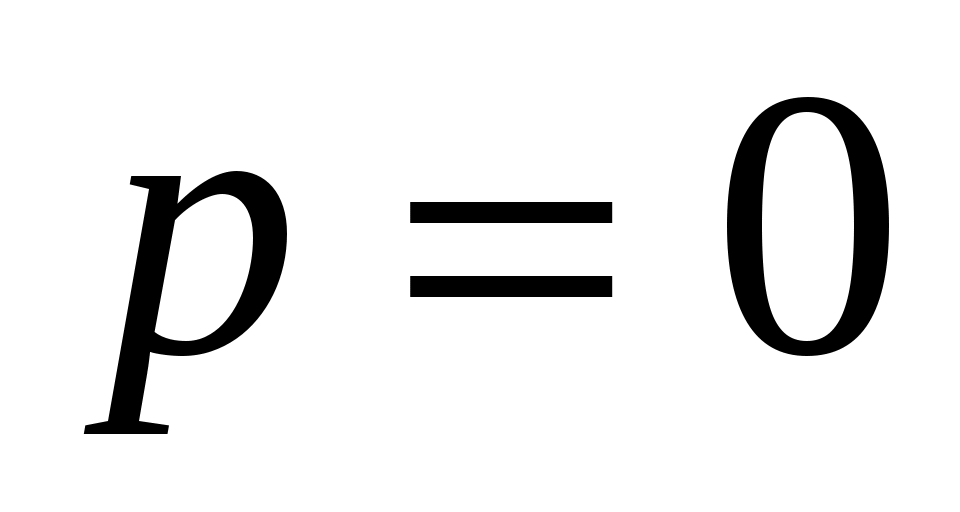 является особым, и, делая обратную замену в этой ситуации, запишем: является особым, и, делая обратную замену в этой ситуации, запишем: 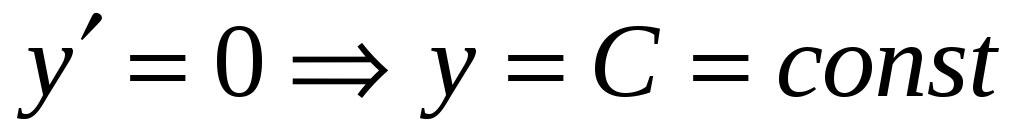 . Оставшееся уравнение . Оставшееся уравнение 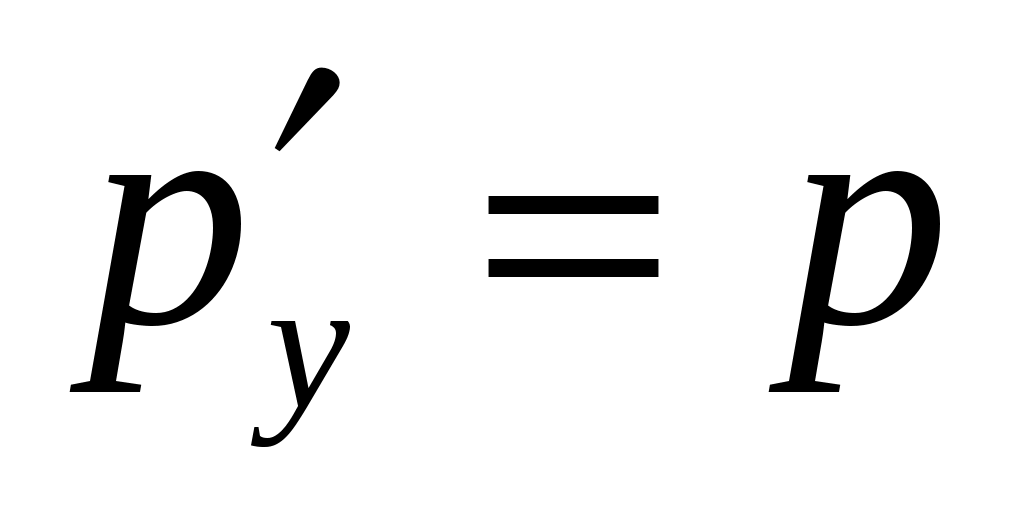 является уравнением в разделяющихся переменных: является уравнением в разделяющихся переменных: 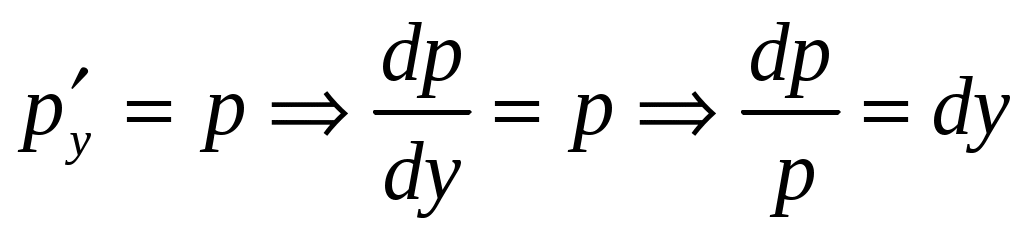 . Интегрируя последнее равенство, получим . Интегрируя последнее равенство, получим 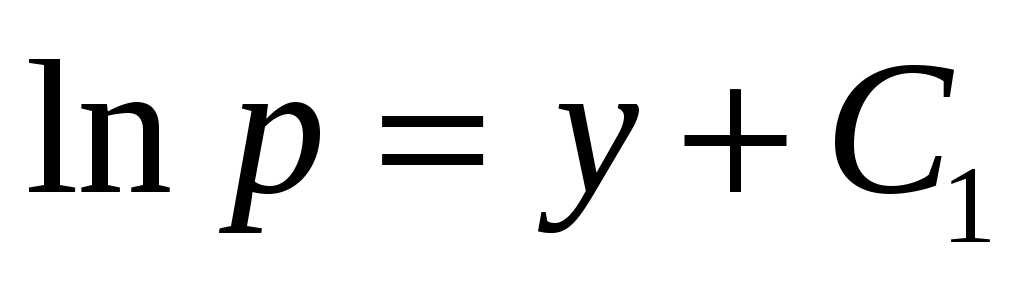 . Выразим теперь функцию . Выразим теперь функцию 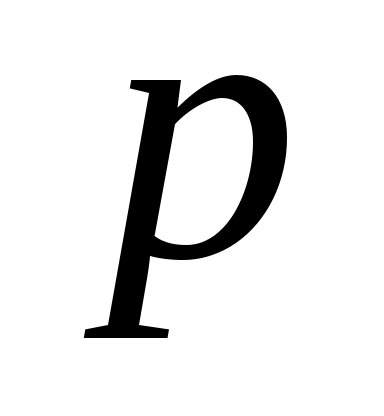 : : 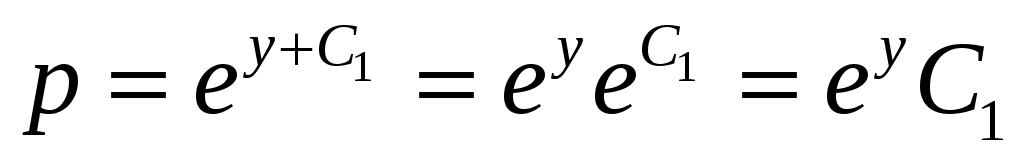 . Делая вновь обратную замену . Делая вновь обратную замену 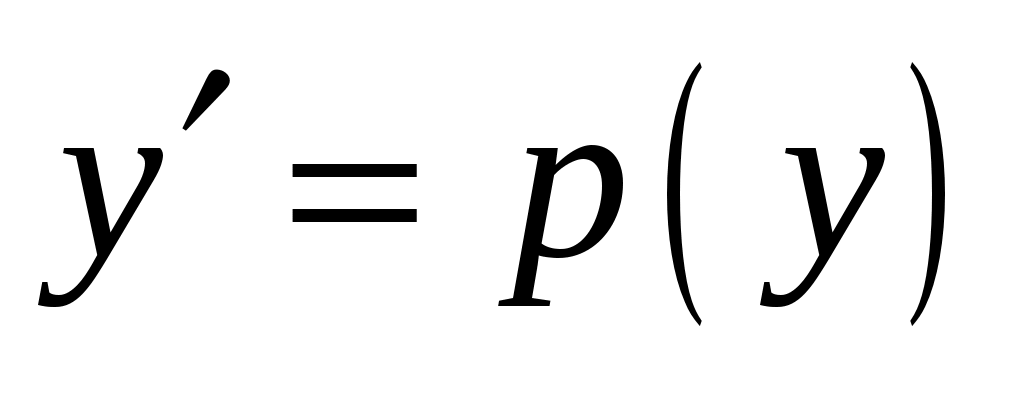 , получим: , получим: 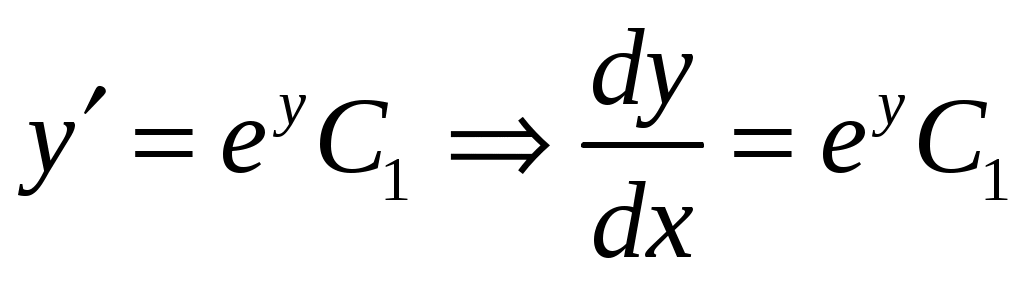 . В данном уравнении можно разделить переменные: . В данном уравнении можно разделить переменные: 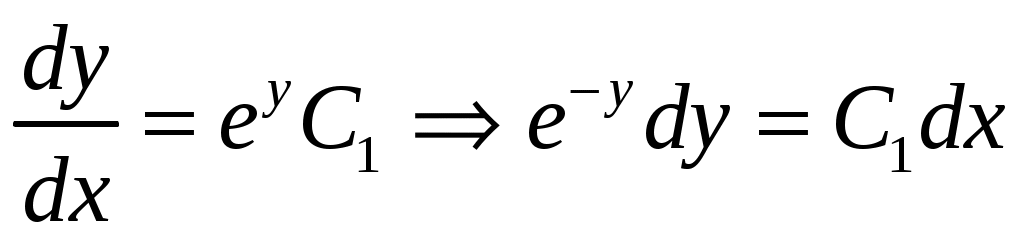 . Интегрируя последнее выражение, получим . Интегрируя последнее выражение, получим 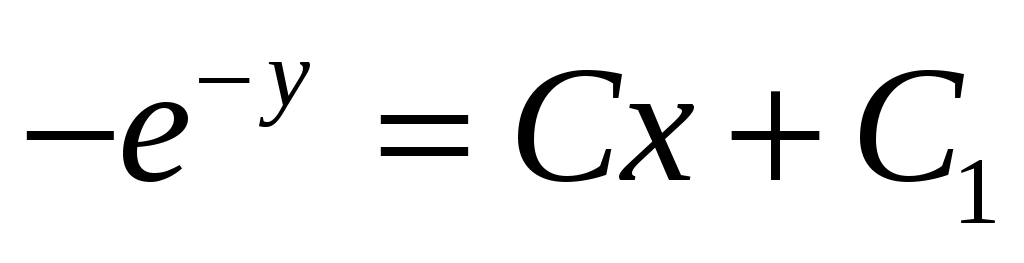 . Получившаяся неявная функция также является решением заданного дифференциального уравнения. . Получившаяся неявная функция также является решением заданного дифференциального уравнения.
|
|
|
 Скачать 0.86 Mb.
Скачать 0.86 Mb.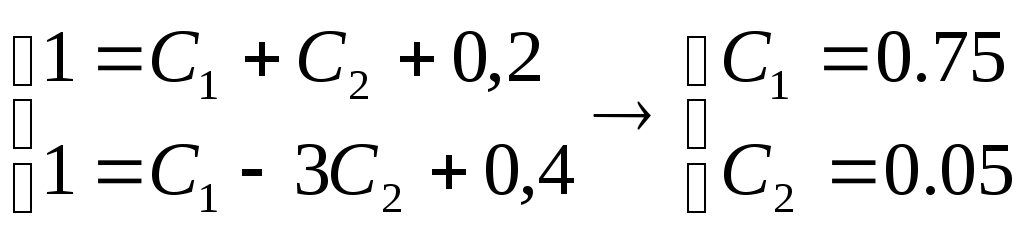
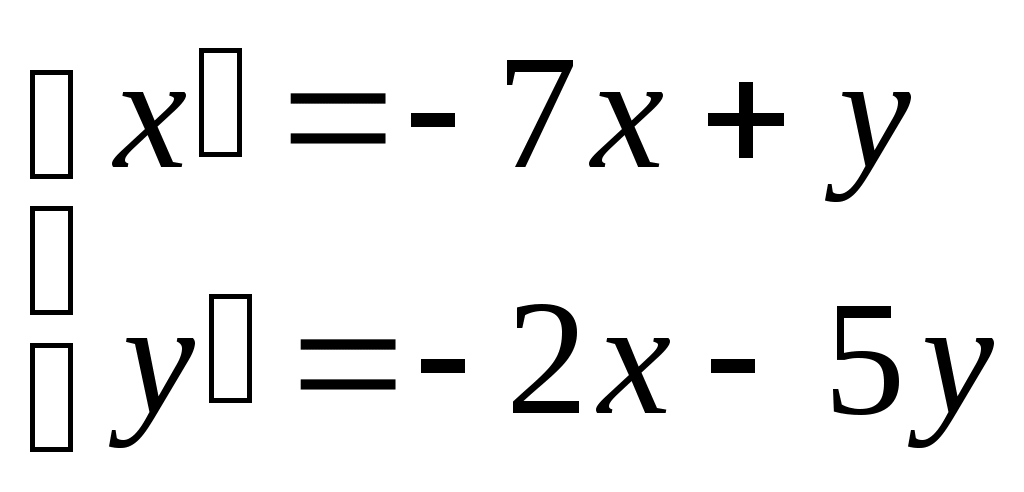 .
.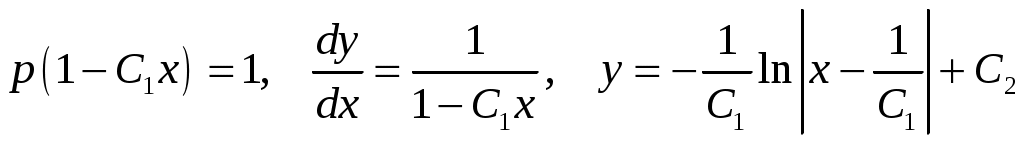 . Учтя, что
. Учтя, что 