Лабораторная работа 2 Приближение функций 2 Лабораторная работа 7 Интерполяция функций. 7 Лабораторная работа 9

• Название: Лабораторная работа 2 Приближение функций 2 Лабораторная работа 7 Интерполяция функций. 7 Лабораторная работа 9
• Дата: 17.03.2023
• Размер: 0.93 Mb.
• Имя файла: Metod_ukaz-ya_po_labam_ChM.doc
• Тип: Лабораторная работа; #997724
• страница: 1 из 6

Оглавление

Лабораторная работа № 1. 2

Приближение функций 2

Лабораторная работа № 2. 7

Интерполяция функций. 7

Лабораторная работа № 3. 9

Построение сплайн-функции. 9

Лабораторная работа № 4. 10

Численные методы решения нелинейных уравнений. 10

Лабораторная работа № 5. 13

Численные методы решения систем уравнений. 13

Лабораторная работа № 6. 25

Численные методы интегрирования. 25

Лабораторная работа № 7. 28

Численные методы решения обыкновенных дифференциальных уравнений. 28

Лабораторная работа №8. 29

Методы численной оптимизации. 29

Список использованной литературы. 35

Лабораторная работа № 1.

Приближение функций

Цель работы: научиться использовать методы вычисления для функций, о которых известна полная информация.

Задание:

Для функций и , рассматриваемых на отрезке и при заданном значении выполнить следующие задания:

1. 
   Разложить функцию в ряд Тейлора с n₁ = 6, n₂ = 11 и n₃ = 20 членами; оценить ошибку аппроксимации в каждом случае.
   
2. 
   Выполнить аппроксимацию данных функций с помощью полиномов Чебышева.
   
3. 
   Произвести экономизацию степенных рядов (разложить функцию в ряд Тейлора и заменить xⁿ полиномами Чебышева)
   

Вариант 1 2 3 4 5 6

Функция f(x)

Функция g(x)

4. 
   Сформулировать вывод о сложности использования и точности применяемых методов.
   

Пример выполнения работы.

1. Разложение функций в ряд Тейлора:

Рассмотрим разложение в ряд Тейлора функции . Общая формула разложения в ряд Тейлора в окрестности точки по степеням имеет вид

, (1)

где - ошибка ограничения, которую можно определить по формуле

, (2)

где находится между и .

Согласно формулам (1) и (2), разложение функции в ряд Тейлора с шестью членами с учётом выглядит так:

.

Ошибка при такой аппроксимации составит

.

Максимально возможное значение ошибки аппроксимации при разложении рассматриваемой функции в ряд Тейлора с шестью членами составляет


Аналогично разложим функцию в ряд Тейлора с одиннадцатью членами:

.

Ошибка при такой аппроксимации составит

.

Максимально возможное значение ошибки аппроксимации при разложении рассматриваемой функции в ряд Тейлора с шестью членами составляет



Разложим функцию 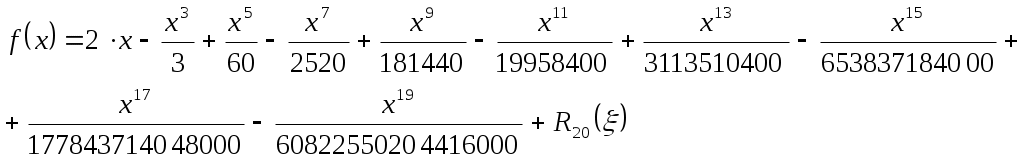в ряд Тейлора с двадцатью членами:

.

Ошибка при такой аппроксимации составит

.

Максимально возможное значение ошибки аппроксимации при разложении рассматриваемой функции в ряд Тейлора с шестью членами составляет



Мы видим, что при повышении порядка аппроксимирующего полинома точность аппроксимации возрастает нелинейно: при разложении функции в ряд Тейлора с 6 членами порядок ошибки ограничения составляет 10^-4, при разложении в ряд с 11 членами – 10^-9, а при использовании ряда с 20 членами – уже 10^-20.
Рассмотрим теперь разложение в ряд Тейлора функции . Снова воспользуемся формулами (1) и (2):

Разложение функции в ряд Тейлора с шестью членами с учётом выглядит так:

.

Ошибка при такой аппроксимации составит



Поскольку порядок степенной функции, разлагаемой в ряд Тейлора, меньше количества членов в этом ряду, аппроксимирующая функция тождественна аппроксимируемой, следовательно, ошибка аппроксимации равна нулю.

Разложение функции в ряд Тейлора с тремя и более членами неактуально, так как такое разложение будет в точности повторять исходную функцию. Соответственно, нет необходимости выполнять разложение в ряды с 11 и 20 членами и вычислять для них ошибку аппроксимации – результаты будут такими же, как в приведённом выше разложении в ряд с 6 членами.

2. Аппроксимация функций с помощью полиномов Чебышева

Любую функцию на отрезке [-1; 1] можно представить как линейную комбинацию полиномов Чебышева :

(3)

Полиномы Чебышева определяются следующим образом:





Или по рекуррентной формуле:



Коэффициенты разложения 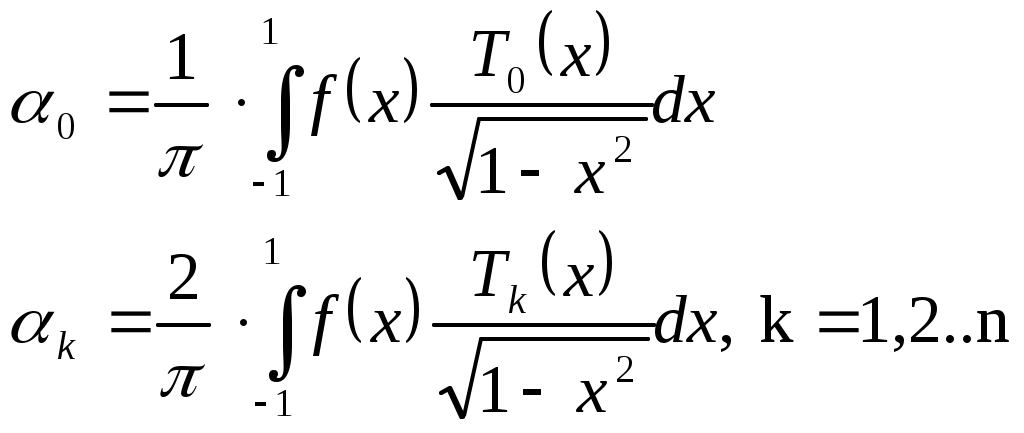определяются по формулам

(4)

Представим исходную функцию в виде линейной комбинации шести полиномов Чебышева, используя формулы (3) и (4):



В общем случае разложение функции полиномами Чебышева выглядит следующим образом:



где n – требуемое количество полиномов Чебышева в разложении функции.
Из результатов расчётов видно, что аппроксимация функций полиномами Чебышева даёт более точные результаты по сравнению с разложением функций в ряд Тейлора, особенно при небольших количествах элементов ряда. При разложении рассматриваемой функции в ряд Тейлора с 6 членами точность расчётов на уровне 10^-4, а при аппроксимации функции линейной комбинацией из 6 полиномов Чебышева – уже 10^-6.

Представим функцию в виде линейной комбинации шести полиномов Чебышева, используя формулы (3) и (4):



Рассчитаем значения функций в точках -1, 0 и 1 и их отклонения от значений исходной функции в этих точках:

3. 
   Экономизация степенных рядов
   

Метод экономизации рядов заключается в корректировке коэффициентов частичной суммы степенного ряда функции f(x). Он состоит из следующей последовательности действий:

1. 
   Вычислить необходимое число коэффициентов степенного ряда для приближения функции f(x) с требуемой точностью на отрезке [a,b];
   
2. 
   Сделать замену переменных для отображения интервала [a,b] в интервал [-1,1];
   
3. 
   Найти коэффициенты разложения полученного полинома по полиномам Чебышева;
   
4. 
   В полученном разложении взять первые k членов так, чтобы коэффициент при T_k+1 по абсолютной величине был меньше необходимой точности вычислений;
   
5. 
   Представить полученную сумму многочленом стандартного вида;
   
6. 
   Сделать обратную замену переменных.
   

Метод экономизации рядов позволяет распространить ошибку ограничения по всему интервалу, при этом уменьшив количество необходимых для вычисления слагаемых.



Для функции .

Из метода разложения функции в ряд Тейлора имеем

С помощью метода приближения функции полиномами Чебышева получим



Полиномы Чебышева представляют собой следующие выражения:



Подставляя T₁ – T₉ в х¹¹, получим



Подставим х¹¹ в выражение для ряда Тейлора:

Значение T₁₁ на рассматриваемом интервале (xϵ[-1;1]) по модулю не превосходит 1; для оценки ошибки примем T₁₁=1:
Отклонение значения полинома f_Э(x) от истинного значения функции составляет








Заметим, что порядок приближающего полинома равен 9. Сравним значение ошибки приближения с ошибкой при использовании ряда Тейлора девятой степени:



Мы видим, что ошибка приближения функции с помощью ряда Тейлора почти в пять раз больше, чем при прближении этой функции полиномом, полученным по методу экономизации степенных рядов (при том же порядке полинома). Из полученных значений можно сделать следующий вывод: экономизация степенного ряда позволяет получить в 5 раз более точный результат, чем обычный ряд Тейлора, при незначительном усложнении вычислений.