эконометрика. Линейных алгебраических уравнений для определения методом наименьших квадратов значений параметров a b уравнения по выборке объема n имеет вид
 Скачать 1.05 Mb.
|
|
Если функция регрессии нелинейная, то оценка значимости ее параметров производится
Система линейных алгебраических уравнений для определения методом наименьших квадратов значений параметров a.b уравнения  по выборке объема n имеет вид:По 25-ти наблюдениям построено уравнение регрессии  . Коэффициент линейной корреляции составил 0,7. После включения в модель фактора индекс множественной корреляции составил 0,8. На уровне значимости 0,05 табличное значение F-критерия равно 4,3. Включение в эконометрическую модель фактора значимо, так как фактическое значение частного F-критерия равно
По наблюдаемым значениям признака-результата Y и факторных признаков вычислены значения величин: Правильным является заключении
Если число коэффициентов эконометрической структурной модели равно числу коэффициентов соответствующей приведенной модели и структурные коэффициенты однозначно определяются по приведенным коэффициентам, то структурная модель называется
Проверка статистической гипотезы об отсутствии гетероскедастичности случайного члена в регрессионной модели по выборкам большого объема требует вычисления статистики по формуле: При построении мультипликативной модели уровня временного ряда скорректированные значения сезонной компоненты вычисляют по формуле: При построении аддитивной модели уровня временного ряда скорректированное значение сезонной компоненты вычисляют по формуле: Результатом преобразования уравнения  к линейному виду относительно параметров регрессии является уравнение:При построении уравнения регрессии по наблюдаемым значениям признаков X и Y с применением метода наименьших квадратов уравнение  следует преобразовать к виду:Случайные колебания в динамике изучаемого показателя объясняются влиянием
Общая вариация зависимой переменной связана с факторной (объясненной) суммой квадратов отклонений для регрессии и с остаточной суммой квадратов отклонений для регрессии
Доля вариации уровней временного ряда, не объясняемая тенденцией, измеряется величиной Если:  , то стандартизованные коэффициенты регрессии  являются решением системы уравнений:Совокупное и долговременное воздействие множества факторов на изменение изучаемого показателя может формировать
Целесообразность включения факторов в модель регрессии можно оценить с помощью
Корреляционная зависимость между значениями случайных остатков  и  при моделировании уровней показателя временного ряда называется
Вычислены частные коэффициенты линейной корреляции первого порядка:  Тогда частный коэффициент линейной корреляции второго порядка равен
По 27-ти наблюдениям за изменениями значений признаков X и Y значение парного коэффициента линейной корреляции составило 0,6. При проверке значимости степени тесноты линейной связи между признаками фактическое значение приемлемого статистического критерия составило
При проверке нулевой гипотезы о несмещенности случайных отклонений  в нелинейных моделях регрессии в качестве статистического критерия рассматривается статистика:Для эконометрической модели, выраженной системой уравнений в отклонениях переменных от их средних 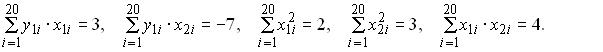 уровней , вычислены значения величин:  Тогда приведенное уравнение регрессии для эндогенной переменной имеет вид:Для эконометрической модели, выраженной системой уравнений  ошибка  в уравнении для эндогенной переменной приведенной формы эконометрической модели
Матрица коэффициентов при эндогенных переменных в системе рекурсивных уравнений может иметь вид: По наблюдаемым значениям признака-результата Y и факторных признаков вычислены значения величин: Правильным является заключение:
Если коэффициент парной линейной корреляции равен 0.6, то коэффициент парной линейной детерминации для тех же данных равен
Пусть:  уравнение регрессии и выборочные дисперсии значений признаков X и Y соответственно. Тогда выборочный коэффициент парной линейной корреляции равен
Критерий Дарбина-Уотсона (DW) и коэффициент автокорреляции остатков связаны равенством: Для данного временного ряда вычислены значения величин:  Коэффициент автокорреляции второго порядка равен
Система четырех одновременных эконометрических уравнений включает m экзогенных переменных. Необходимое условие точной идентифицируемости уравнения  выполняется приСистема линейных алгебраических уравнений для определения методом наименьших квадратов значений параметров a,b уравнения  по выборке объема n имеет вид:Для сопоставления факторов по силе влияния на изменение признака-результата можно пользоваться
Если остатки  и объясняющая (независимая) переменная не коррелированны, то:Пусть: уравнение регрессии и выборочные дисперсии значений признаков X и Y соответственно. Тогда выборочный коэффициент парной линейной корреляции равен
Исследование нелинейных моделей регрессии на несмещенность случайных отклонений сводится к проверке статистической гипотезы По 25-ти наблюдениям построено уравнение регрессии  . Индекс множественной корреляции составил 0,7. На уровне значимости 0,05 табличное значение F-критерия равно 3,35. Построенная регрессионная модель значима, так как фактическое значение F-критерия равно
Если:  , то стандартизованные коэффициенты регрессии являются решением системы уравнений:Регрессией, нелинейной относительно оцениваемых параметров, является уравнение Для оценки значимости уравнения множественной регрессии используют
Долю вариации зависимой переменной, объясненную вариацией факторов, включенных в модель множественной регрессии, характеризует
Для проверки значимости выборочного коэффициента парной линейной корреляции используют критерий
По данным, характеризующим некоторый объект за несколько последовательных моментов или периодов времени, можно построить
Расчету оценки сезонной компоненты в модели уровня временного ряда предшествует
В уравнении регрессии  величины a,b являются
Для эконометрической модели, выраженной системой уравнений в отклонениях переменных от их средних уровней , вычислены значения величин:  Тогда приведенное уравнение регрессии для эндогенной переменной имеет вид:Приведенная форма некоторой структурной модели может быть выражена системой уравнений: За последовательные 4 года по каждому кварталу вычислены суммы значений оценки сезонной компоненты:  Скорректированные значения сезонной компоненты равны соответственно: При использовании ступенчатого регрессионного анализа при выборе наилучшей эконометрической регрессионной модели повторяется процедура определения зависимости случайных остатков текущей модели
При моделировании тенденции в динамике показателя уравнением  вычислены значения величин:  Тогда оценки параметров тренда
Исследование стабильности (постоянства) дисперсии случайных отклонений в моделях регрессии сводится к проверке статистической гипотезы о равенстве
Результатом преобразования уравнения  к линейному виду относительно параметров регрессии является уравнение:Если:  , то значение выборочного коэффициента парной линейной корреляции (с точностью 0,01) равно
Для эконометрической модели, выраженной системой уравнений  свободный член уравнения регрессии для приведенной формы эконометрической модели
Матрица коэффициентов при экзогенных переменных приведенной формы эконометрической модели может иметь вид: Автокорреляция уровней временного ряда – это корреляционная связь между последовательными значениями
Если значение выборочного коэффициента парной линейной корреляции близко к нулю, то можно предположить, что
Для эконометрической модели, выраженной системой уравнений в отклонениях переменных от их средних уровней , вычислены значения величин:  Тогда приведенное уравнение регрессии для эндогенной переменной имеет вид:За последовательные 4 года по каждому кварталу вычислены суммы значений оценки сезонной компоненты:  Скорректированные значения сезонной компоненты равны соответственно:Пусть: Y – признак-результат;  –признаки - факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков  и построено уравнение регрессии в стандартизованном масштабе  . Тогда теоретические (расчетные) значения признака-результата вычисляют по формуле:Уравнение  , отражающее корреляционную связь между признаком-результатом Y и признаками-факторами , это –
Если |
