Матем. КР1 для психологов. Матрицы. Операции над матрицами
 Скачать 1.53 Mb.
|
|
МАТРИЦЫ. ОПЕРАЦИИ НАД МАТРИЦАМИ. Матрицы. Определение. Матрицей размера  называется таблица чисел, состоящая из  строк и  столбцов. Числа, составляющие матрицу, называются элементами матрицы.Матрицы обозначаются прописными буквами латинского алфавита (например А, В, С), а элементы матрицы – строчными буквами с двойной индексацией:  , где  – номер строки,  – номер столбца.Например, матрица 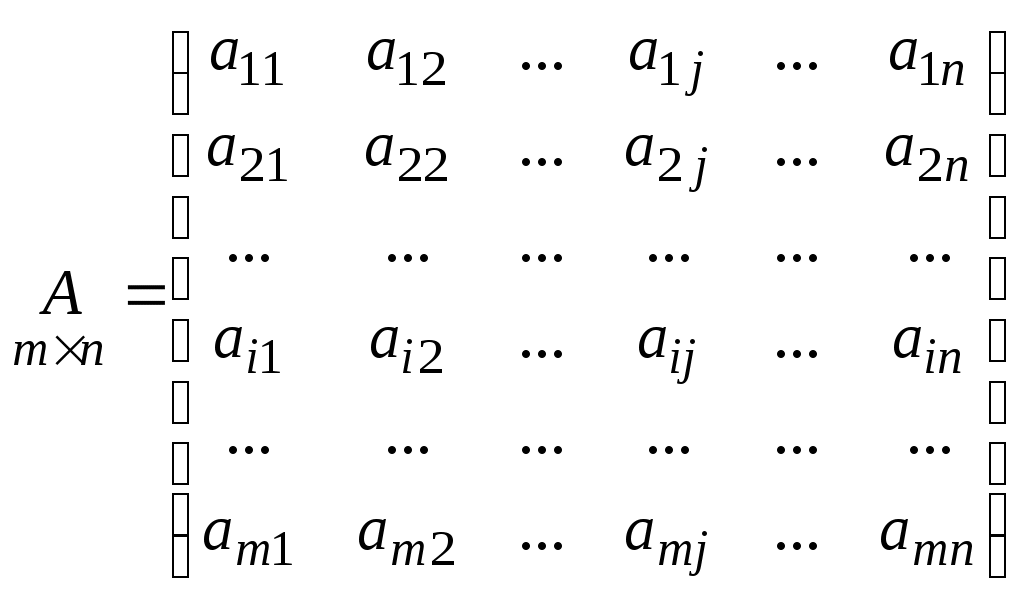 ,или в сокращенной записи  , где  ;  .Виды матриц. Матрица, состоящая из одной строки, называется матрицей (вектором)–строкой, а из одного столбца – матрицей (вектором)–столбцом: 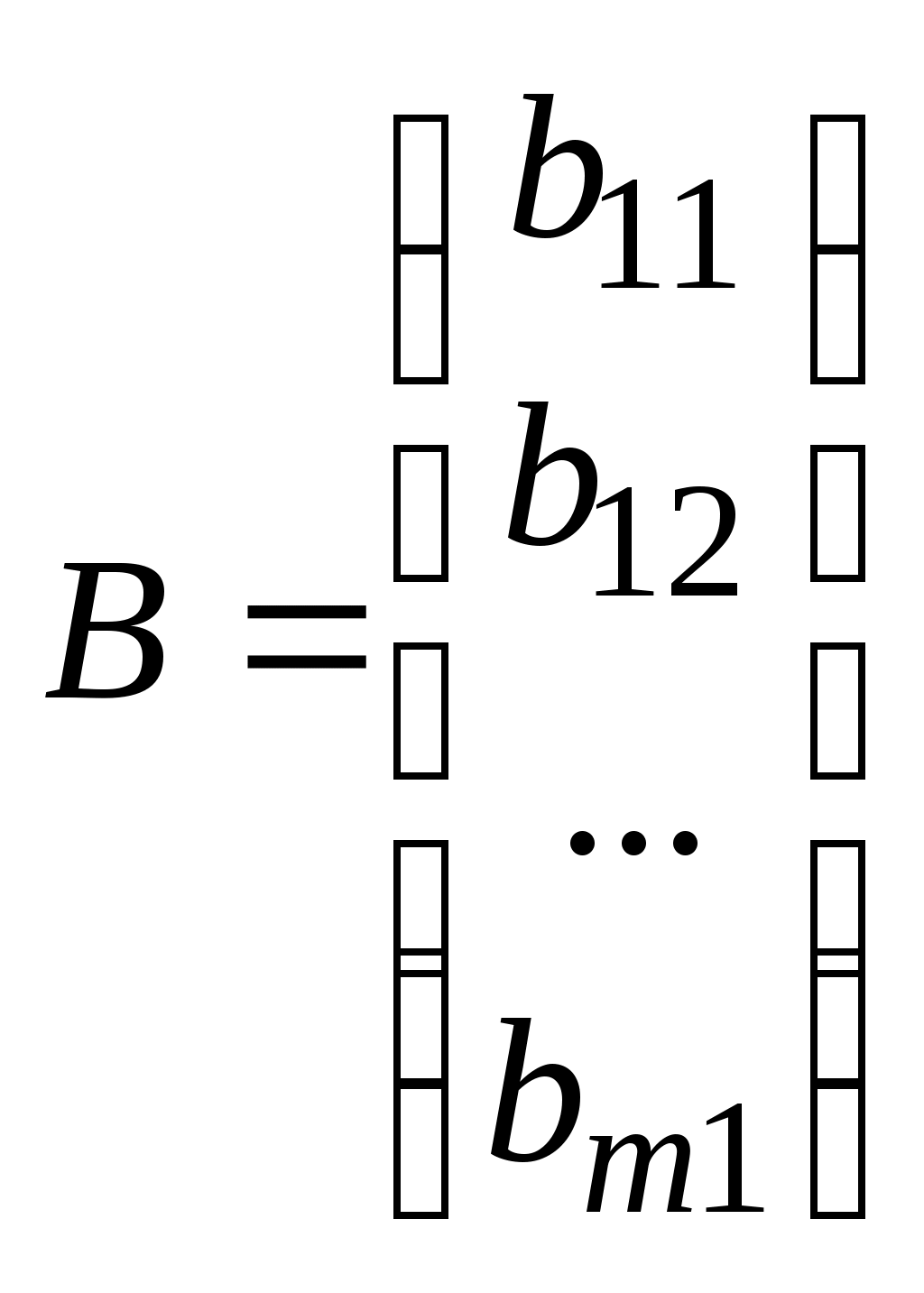 – матрица–строка; – матрица–столбец. Матрица называется квадратной 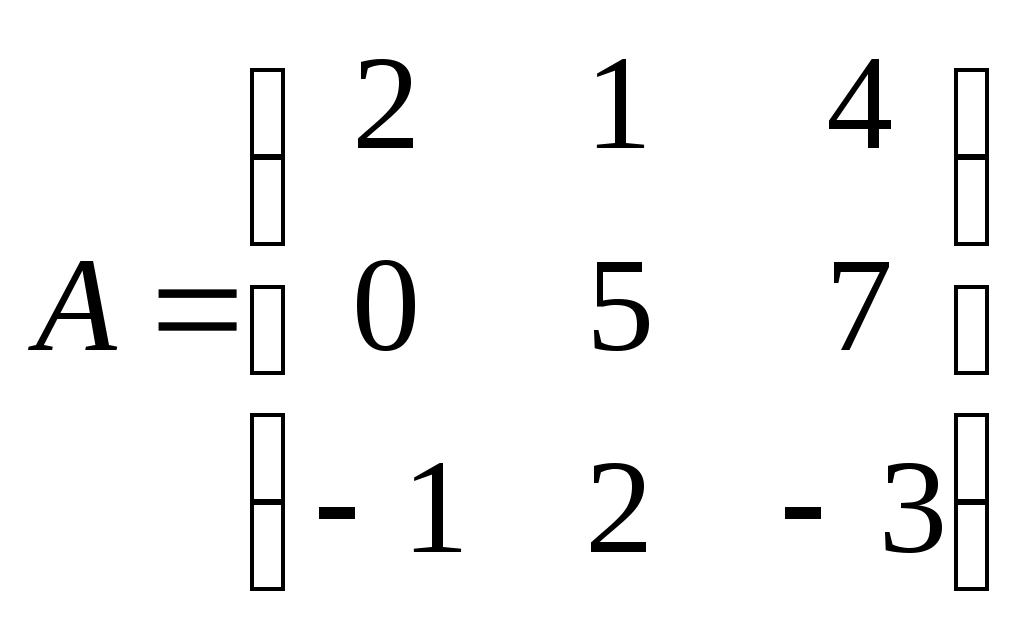 -го порядка, если число ее строк равно числу столбцов и равно . Например,  – квадратная матрица третьего порядка. Элементы матрицы  , у которых номер строки равен номеру столбца  , называются диагональными и образуют главную диагональ матрицы.Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Например, 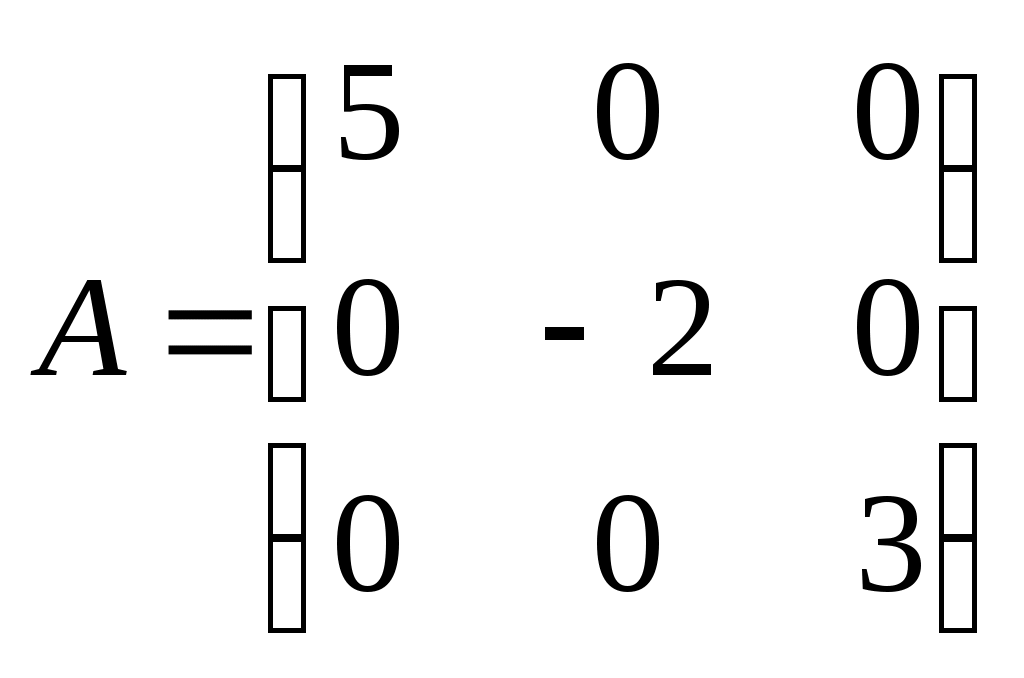 –диагональная матрица третьего порядка.Если у диагональной матрицы 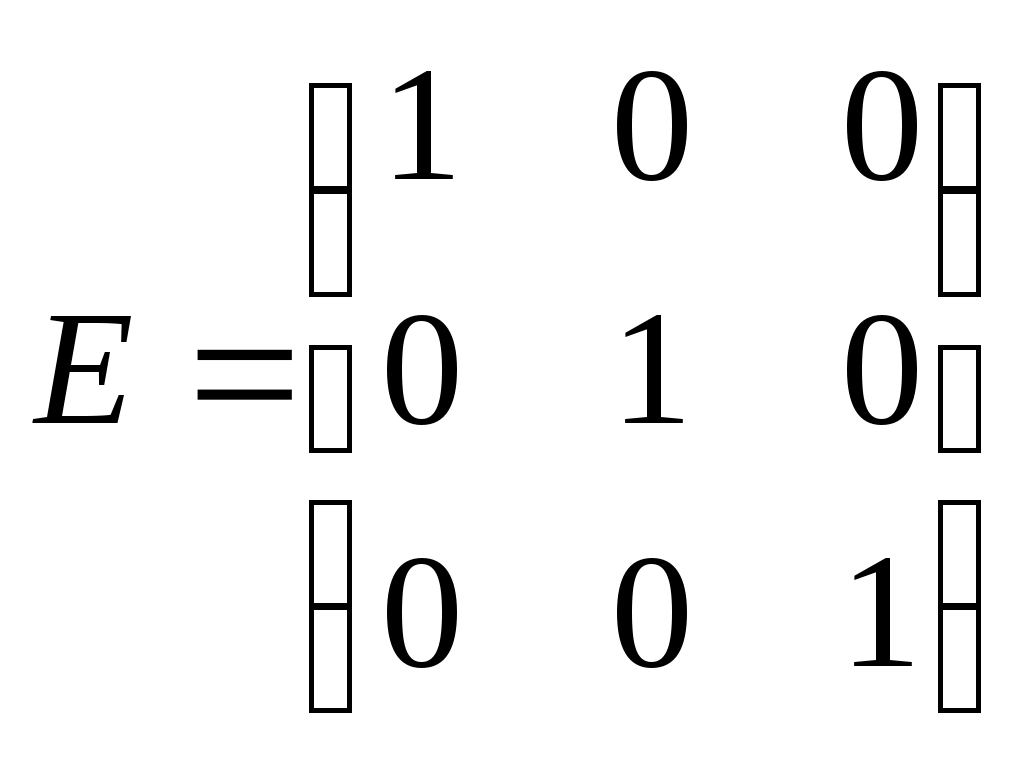-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей -го порядка и она обозначается буквой  . Например,  – единичная матрица третьего порядка.Операции над матрицами. Умножение матрицы на число. Произведением матрицы  на число  называется матрица  , элементы которой  для  ;  .Например, если  , то  .Сложение матриц. Суммой двух матриц и  одинакового размера  называется матрица  , элементы которой  для ; (то есть матрицы складываются поэлементно).Например:  ,  ,  .Умножение матриц. Умножение матрицы на матрицу определено, когда число столбцов матрицы равно числу строк матрицы . Тогда произведением матриц  называется матрица  , каждый элемент которой  равен сумме произведений элементов -ой строки матрицы на соответствующие элементы -го столбца матрицы : Пример. Вычислить произведение матриц 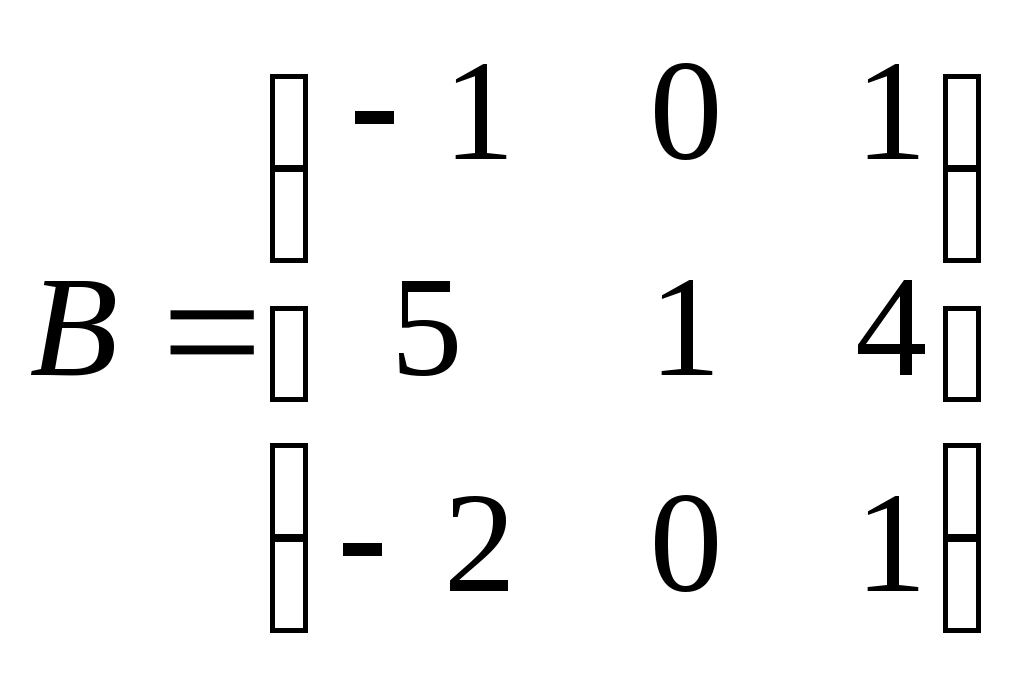 , где  ;  .Найдем размер матрицы-произведения (если умножение матриц возможно):  . Вычислим элементы матрицы  . Элемент получается при умножении -ой строки матрицы на -ый столбец матрицы . ; ; ; ; ; .Получаем  .Транспонирование матрицы – переход от матрицы 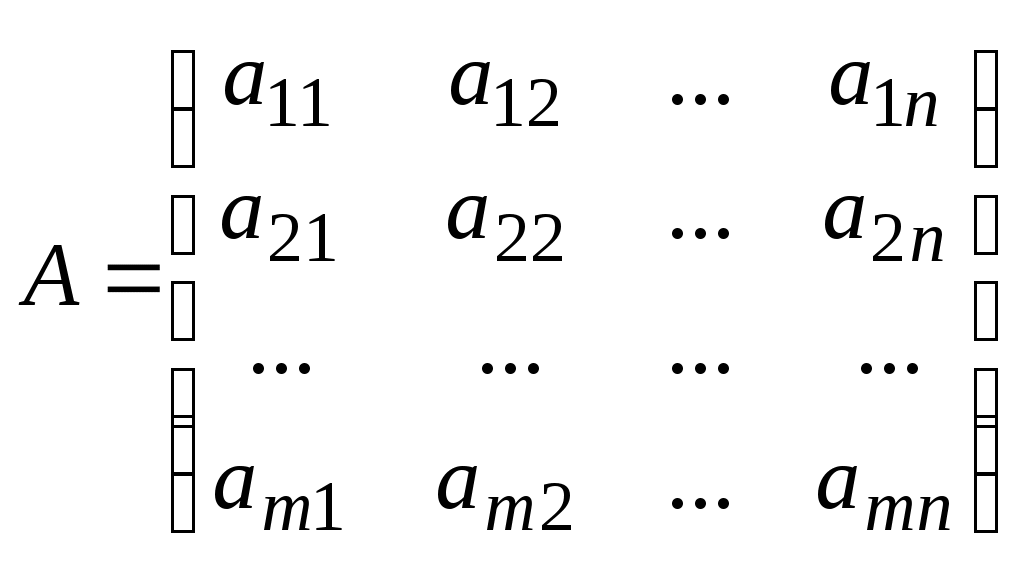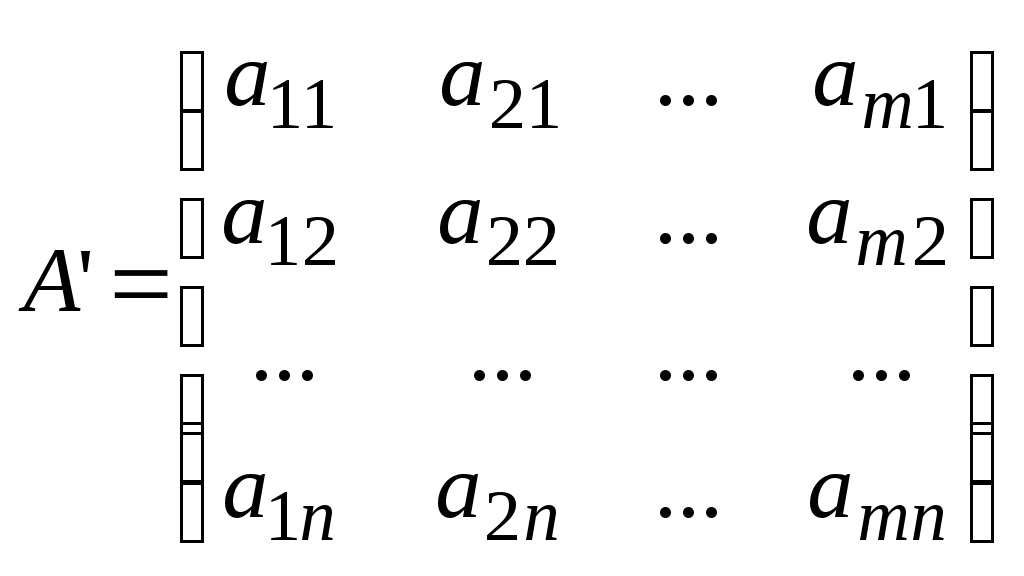к матрице  , в которой строки и столбцы поменялись местами с сохранением порядка. Матрица называется транспонированной относительно матрицы . ,  .Из определения следует, что если матрица имеет размер , то транспонированная матрица имеет размер .Например: 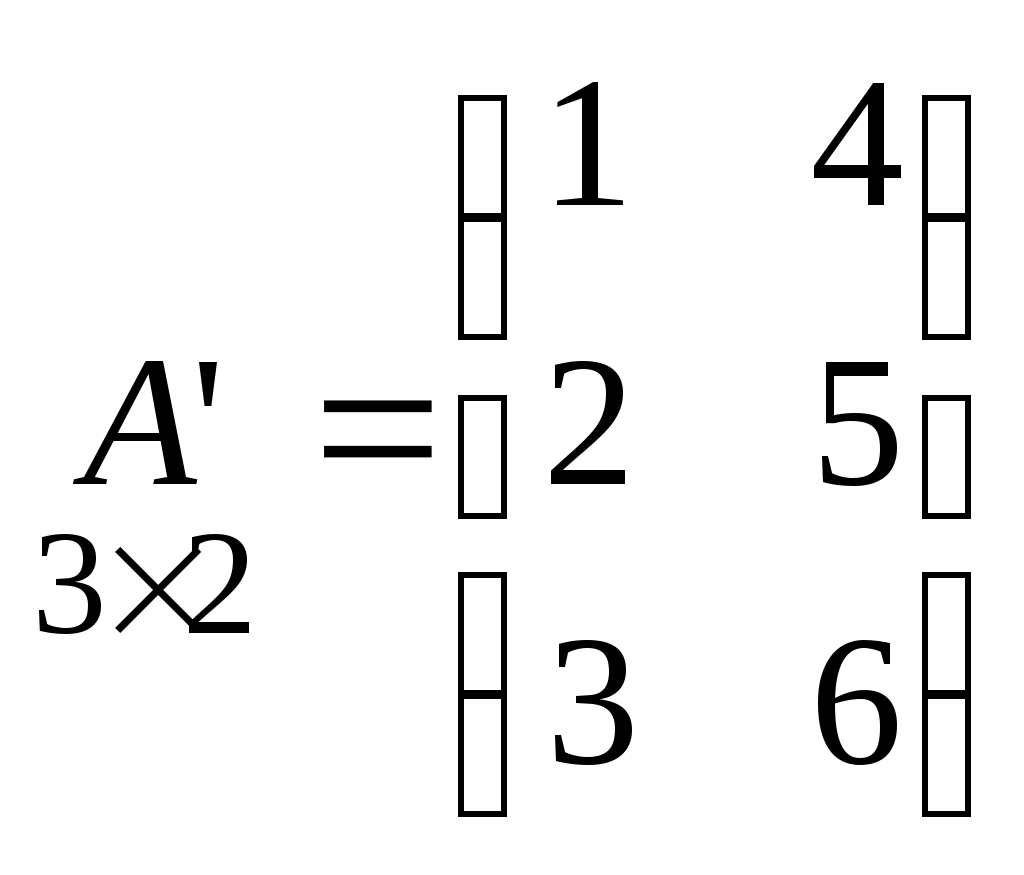 ;  .Определители квадратных матриц Определитель – это число, характеризующее квадратную матрицу. Определитель матрицы обозначается  или  .Определителем матрицы первого порядка  , или определителем первого порядка, называется элемент  : . Например, пусть  , тогда  .Определителем матрицы второго порядка  , или определителем второго порядка, называется число, которое вычисляется по формуле: .Произведения  и  называются членами определителя второго порядка. Например, пусть  , тогда  .Пусть дана квадратная матрица третьего порядка:  .Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:   Рис. 1. Это число представляет собой алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строка и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу, легко запомнить, пользуясь схемой (рис.1.), которая называется правилом треугольников или правилом Сарруса. Для вычисления определителей более высоких порядков потребуются некоторые дополнительные понятия. Пусть дана квадратная матрица n-го порядка.Минором  элемента матрицы n-го порядка называется определитель матрицы (n–1)-го порядка, полученной из матрицы вычеркиванием -ой строки и -го столбца.Например, минором элемента 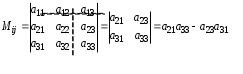 матрицы третьего порядка будет: Алгебраическим дополнением  элемента матрицы n-го порядка называется его минор, взятый со знаком  :  , т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца (i+j) – четное число, и отличается от минора знаком, когда (i+j) – нечетное число. Например,  ;  .Для вычисления определителей квадратных матриц выше третьего порядка пользуются теоремой Лапласа. Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:  (разложение по элементам i-й строки;  ); (разложение по элементам j-го столбца; );По свойствам определителей, определитель матрицы не изменится, если к элементам любой строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число. Это свойство определителей и теорема Лапласа позволяют существенно упростить вычисление определителей высоких порядков. При вычислении определителей нужно преобразовать исходную матрицу так, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу). Пример. Вычислить определитель четвертого порядка: 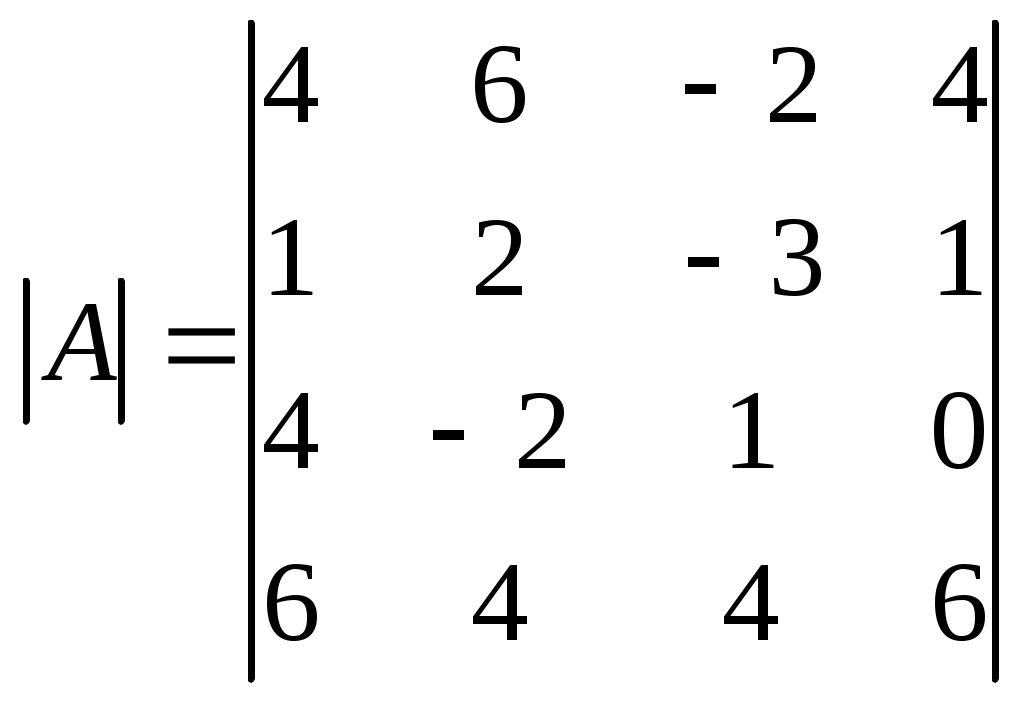 .Преобразуем матрицу так, чтобы в 3-й строке все элементы, кроме одного, обращались в 0. Для этого умножим элементы 3-го столбца на (-4) и на 2 и прибавим их соответственно к элементам 1-го и 2-го столбцов. Раскладывая полученный определитель по элементам третьей строки, найдем 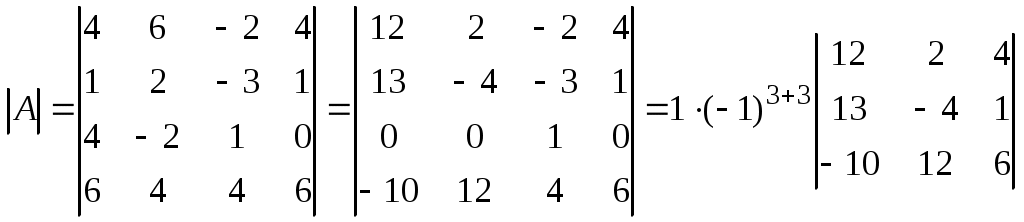 .Полученный определитель третьего порядка можно вычислить по правилу треугольников или с помощью теоремы Лапласа, однако, можно продолжить упрощение матрицы. "Обнулим" в матрице третьего порядка элементы 2-ой строки (кроме одного). Для этого элементы третьего столбца матрицы, предварительно умножив на (-13) и на 4, сложим с элементами 1-го и 2-го столбцов соответственно: 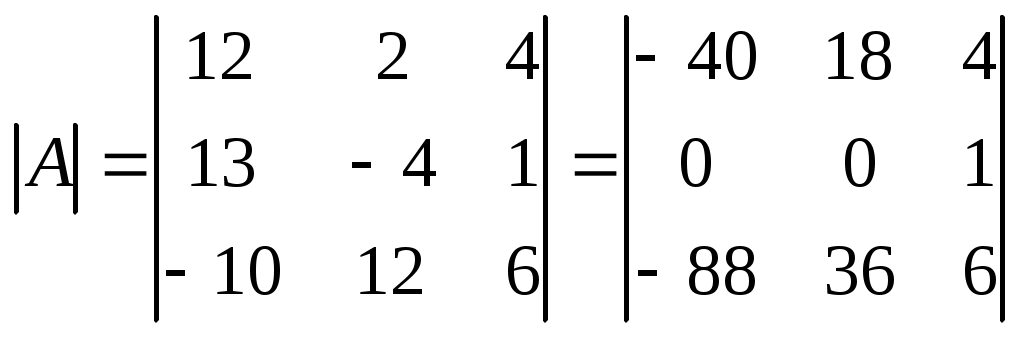 .Раскладывая по элементам второй строки и вынося общие множители, получаем:  . |