Методические рекомендации по выполнению итоговой контрольной работы для специальности 09. 02. 07
 Скачать 6.51 Mb. Скачать 6.51 Mb.
|
 Методические рекомендации по выполнению итоговой контрольной работы для специальности 09.02.07 «Информационные системы и программирование» по дисциплине «Элементы высшей математики» Составитель Булгакова Ирина Викторовна г. Бийск 2021 Пособие предназначено для оказания помощи студентам заочного отделения при выполнении домашней контрольной работы по математике или по элементам высшей математики. Пособие включает в себя некоторые разделы, имеющиеся в этих курсах. Пособие может быть использовано студентами дневной формы обучения. Методические рекомендации для обучающихся по выполнению контрольной работы по учебной дисциплине составлены в соответствии с Федеральным государственным образовательным стандартом, рабочим учебным планом, рабочей программой и календарно-тематическим планом учебной дисциплины ЕН.01 Элементы высшей математикипо специальности среднего профессионального образования 230115 Программирование в компьютерных системах (углубленной подготовки). Контрольная работа является одной из форм проверки и оценки усвоенных знаний, получения информации о характере познавательной деятельности, уровня самостоятельности и активности студентов в учебном процессе, эффективности методов способов учебной деятельности. Цель: выявление знаний студентов по изученному материалу; понимания сущности получаемых знаний и навыков, необходимых для осуществления профессиональной деятельности. Выполнение студентами контрольной работы и направлено на: - обобщение, систематизацию, закрепление полученных теоретических знаний; - реализация единства интеллектуальной и практической деятельности; - развитие интеллектуальных, аналитических умений у будущих специалистов; - выработку при решении поставленных задач таких профессионально значимых качеств, как ответственность, самостоятельность. 1.Результаты освоения дисциплины, подлежащие проверке в процессе выполнения контрольной работы 1.1. В результате изучения учебной дисциплиныобучающийся должен: уметь: - выполнять операции над матрицами и решать системы линейных уравнений; - решать задачи, используя уравнения прямых и кривых второго порядка на плоскости; - применять методы дифференциального и интегрального исчисления; - решать дифференциальные уравнения; - пользоваться понятиями комплексных чисел; знать: - основы математического анализа, линейной алгебры и аналитической геометрии; - основы дифференциального и интегрального исчисления; - основы теории комплексных чисел. В результате выполнения контрольной работы по учебной дисциплине осуществляется комплексная проверка знаний и умений полученных по учебной дисциплине в соответствии с программой. Курс «Математика» входит в цикл математических и общих естественнонаучных дисциплин В результате изучения дисциплины, обучаемый должен иметь представление о роли математики в современном мире, общности ее понятий и представлений; знать основные понятия дифференциального и интегрального исчисления; уметь использовать методы дифференциального и интегрального исчисления при решении прикладных задач. Содержание дисциплины «Математика» имеет тесную связь с другими дисциплинами учебного плана: «Экономическая теория», «Экономический анализ», «Финансовая математика», «Информатика». Программа дисциплины состоит из 3 разделов. В ходе изучения I раздела обучаемые получают представление о пределе функции в точке и на бесконечности и двух так называемых «замечательных пределах», наиболее часто используемых в анализе; знания о свойствах пределов и непрерывных функций, типах точек разрыва функции; умения вычислять несложные пределы, устанавливать непрерывность функции и точки ее разрыва. В разделе II изучаются производные функции и их применения для исследования функций. После его изучения обучаемых должны знать табличные значения производных элементарных функций и правила дифференцирования, уметь находить производную сложной функции и производные высших порядков, применять производные для нахождения точек экстремума и перегиба функции. После изучения III раздела обучаемые должны иметь представление о свойствах неопределенного и определенного интегралов, знать методы из вычисления и уметь решать несложные задачи на применение определенного интеграла. Изучения каждой темы курса следует начинать с ознакомления с содержанием ее программы. Затем необходимо изучить рекомендуемую литературу, ответить на вопросы и решить задачи для самопроверки Рекомендации по оформлению Контрольная работа выполняется по одному из вариантов, номер которого для каждого студента определяется по Контрольная работа выполняется в отдельной тетради и представляется на проверку в срок, установленный учебным графиком. Если работа не зачтена, необходимо ознакомиться с замечаниями преподавателя и выполнить ее повторно. По вопросам, возникающим в процессе выполнения заданий, следует обращаться за консультацией. Комплексная контрольная работа по дисциплине «Элементы высшей математики» Контрольная работа составлена по трем основным темам и содержит 21 задание.   Номер задания формируется следующим образом: номер задания . вариант Номер задания формируется следующим образом: номер задания . вариантт.е. чтобы выбрать 3 задание 5 варианта нужно выполнить задание с номером 3.5 Решение типового варианта Задание 1. Дано комплексное число z. Найти Re z, Imz, z, arg z, 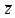 . Построить числа z и . Построить числа z и 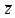 в одной системе координат: z = 9+7i в одной системе координат: z = 9+7iРешение: Re z =9, Imz=7, z, arg z 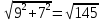   7  9  -7 Ответ: 9; 7; 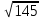 Задание 2. Вычислить значение выражения: а) 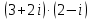 Решение: 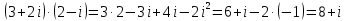 Ответ: 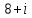 Рассмотрим частные случаи степеней мнимых единиц 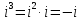 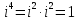 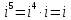 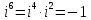 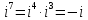 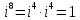 б) 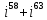 Решение: 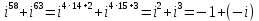 Ответ: 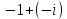 в) 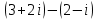 Решение: 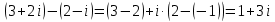 Ответ: 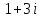 г) 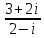 Решение: 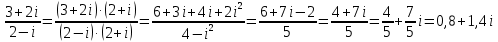 Ответ: 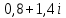 Задание 3. Даны матрицы А и В. Найдите 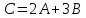 , если: , если: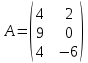 B= 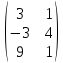 Решение 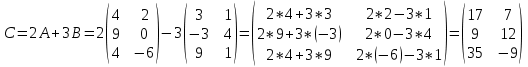 З  адание аданиеДаны две матрицы. Умноте из на друга Задание 4. Решить систему уравнений матричным методом (с помощью обратной матрицы), по правилу Крамера или методом Гаусса. 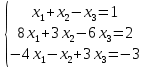 Решение:  1. Метод Гаусса. Умножим первое уравнение на −8 и прибавим его ко второму, умножим первое уравнение на 4 и прибавим к третьему. Таким образом, исключили переменную x1 из второго и третьего уравнений: 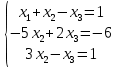 Умножим второе уравнение на 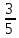 и прибавим к третьему, исключили переменную x2 из третьего уравнения: и прибавим к третьему, исключили переменную x2 из третьего уравнения: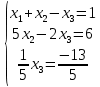 Последовательно находим значения переменных. Так, из третьего уравнения получим 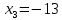 , а из второго , а из второго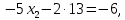 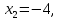 Подставляя значения 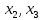 в первое уравнение, найдём в первое уравнение, найдём 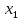 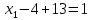 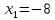 Получили набор чисел 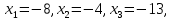 который следует проверить подстановкой в исходную систему. который следует проверить подстановкой в исходную систему.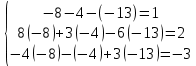 Получили верные числовые равенства, следовательно, набор чисел 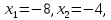 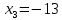 Является решением системы. 2. Метод обратной матрицы. Используя правило умножения матриц, запишем систему в матричном виде AX = B, где 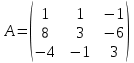 , , 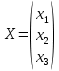 , , 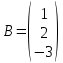 . .Если 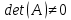 , то существует оратная матрица для A и единственное решение системы находится по формуле , то существует оратная матрица для A и единственное решение системы находится по формуле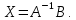 Найдём определитель матрицы A разложение по первой строке: 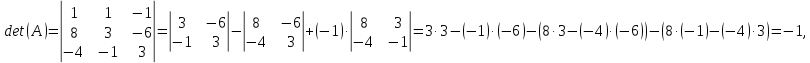 То есть 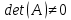 . . Вычислим алгебраические дополнения для каждого элемента матрицы A. 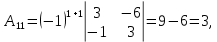 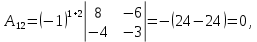 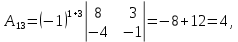 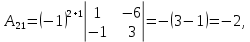 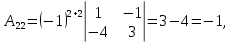 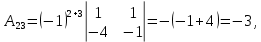 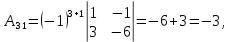 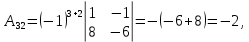 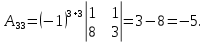 Зная алгебраические дополнения 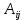 , можем записать союзную матрицу , можем записать союзную матрицу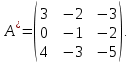 Учитывая, что 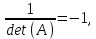 вычислим обратную матрицу по правилу вычислим обратную матрицу по правилу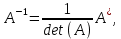 Таким образом, 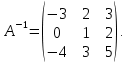 Найдём решение системы 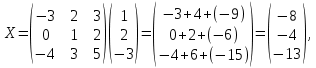 То есть 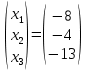 . .Отсюда получаем, что 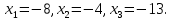  Задание 5. Даны координаты вершин треугольника ABC: A(-6, 3), B(-2,6), C(-2,3). Найти: 1) уравнения сторон треугольника АВС; 2) уравнение высоты СН, опущенной из вершины C на сторону AB; 3) уравнение медианы к стороне AC; 4) угол A; 5) сделать чертеж в системе декартовой координат OХУ Р  ешение: ешение: 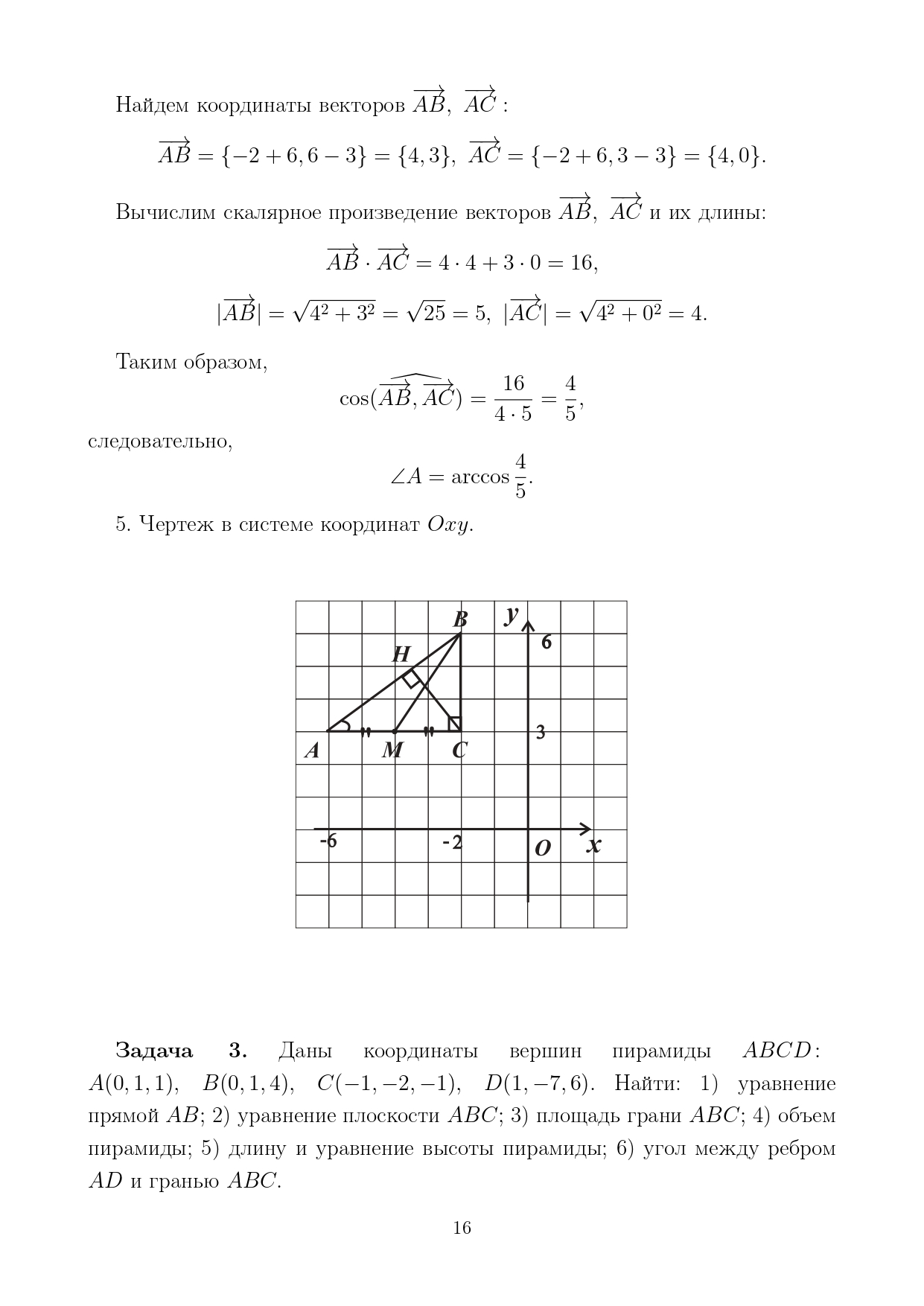 Задание 6. Используя преобразование параллельного переноса, привести уравнение линии второго порядка к каноническому виду и схематично построить кривую. a) x2 + 2x + 2y2 – 4y+1 = 0 b) 3x +2 y2+ 2y +7 = 0 Решение:     Задание 7. Вычислить предел числовой последовательности: а) 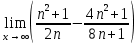 Решение: Сначала преобразуем выражение, стоящее под знаком предела, приводя дроби к общему знаменателю: 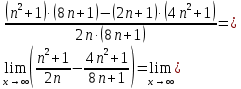 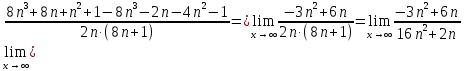 Разделим и числитель, и знаменатель дроби на n в наивысшей степени, т.е. на n2, получим: 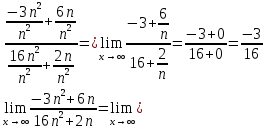 Ответ: 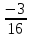 б) 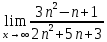 Решение: Разделим и числитель, и знаменатель дроби на n в наивысшей степени, т.е. на n2, получим: 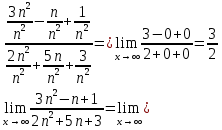 Ответ: 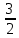 Задание 8. Вычислить значения выражений с использованием замечательных пределов a) 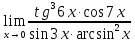 Решение: 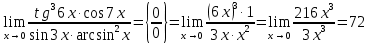 Ответ: 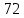 б) 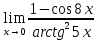 Решение: 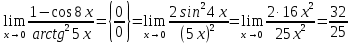 Ответ: 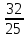 |
