Методические рекомендации по выполнению контрольной работы по дисциплине Методы оптимизации

• Название: Методические рекомендации по выполнению контрольной работы по дисциплине Методы оптимизации
• Дата: 12.01.2022
• Размер: 486 Kb.
• Имя файла: ЊҐв®¤ЁзҐбЄЁҐ гЄ%A0§%A0­Ёп Є Љђ 1.doc
• Тип: Методические рекомендации; #328797
• страница: 1 из 4

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ДГТУ)
Кафедра «Вычислительные системы и информационная безопасность»

Методические указания к контрольной работе по дисциплине «Методы оптимизации»

для студентов 2-го курса

направления подготовки 09.03.02 Информационные системы и технологии

заочной формы обучения

Ростов-на-Дону

2017 г.

Составители:

к.т.н., доцент, А.Ю. Полуян

УДК 681.3

Подготовлено на кафедре «Вычислительные системы и информационная безопасность»

Методические рекомендации

по выполнению контрольной работы по дисциплине
«Методы оптимизации»

/ ДГТУ, Ростов-на-Дону, 2017, 96 с.

Методические рекомендации по выполнению контрольной работы по дисциплине для студентов заочной формы обучения представляют собой комплекс рекомендаций и разъяснений, позволяющих студенту оптимальным образом организовать процесс выполнения курсовой работы.
Введение

Целью изучения дисциплины «Методы оптимизации» является подготовка бакалавров к деятельности, связанной с использованием языков программирования для решения профессиональных задач. При изучении данного курса у студентов формируются знания, и навыки, необходимые для разработки программного обеспечения и сопроводительной документации.

Задачи дисциплины:

1) изучение основных подходов к организации процесса разработки программного обеспечения;

2) выработка навыков использования языков программирования при решении практических задач профессиональной сферы;

3) выработка способности поддерживать работоспособность информационных систем и технологий в заданных функциональных характеристиках и соответствии критериям качества.

1. 
   Связь с предшествующими и последующими дисциплинами (модулями, практиками, научно-исследовательской работой (НИР) в соответствии с ОПОП.
   

Для успешного усвоения дисциплины Методы оптимизации необходимо, чтобы студент владел знаниями, умениями и навыками, сформированными в процессе изучения дисциплин:

— Численные методы;

— Высшая математика.

1. 
   Алгоритм выбора варианта контрольной работы
   

Контрольная работа заключается в выполнении 2 заданий, приведенных в данном документе. Номер варианта есть число равное сумме двух последних цифр зачетки.

Задание № 1

«Безусловный экстремум функции двух переменных»

(методические указания)
Цель контрольной работы: Исследование стационарных точек функции двух переменных, определяемых аналитическим методом

Задание: Для функции f(x,y) и уравнения связи g(x,y)=0 найти аналитическим методом:

1) координаты стационарных точек функции f(x,y), воспользовавшись необходимыми условиями экстремума с проверкой результатов решения уравнений;

2) определить вид каждой из стационарных точек (максимум, минимум, нет экстремума), воспользвавшись достаточными условиями экстремума.

При несоблюдении требований правила проверки достаточного условия (B²– АС = 0,разные знаки у А и С и т.д.) указать, по какой причине заключение о характере соответствующей стационарной точки сделать нельзя.

При выполнении преобразований делать максимальные упрощения с использованием правильных дробей, а все конечные численные значения координат и значений функций указывать в десятичной форме с округлением дробной части до трёх знаков (например, вместо 5/3 записать 1,66(6), а вместо значение 2,628);

3) Результаты выполнения задания оформить в виде отчёта.


Задания для выполнения контрольной работы
Варианты задания 1

1		g(x,y) = 3x + y – 3 = 0
2		g(x,y) = 4x – 2y + 1 = 0
3		g(x,y) = 5x -2y + 2 = 0
4		g(x,y) = 6x – 3y – 1 = 0
5		g(x,y) = 3x + 6y – 4 = 0
6		g(x,y) = 2x -2y + 6 = 0
7		g(x,y) = 3x + y – 1 = 0
8		g(x,y) = 3x – 4 y + 1 = 0
9		g(x,y) = 2x – 2y –1 = 0
10		g(x,y) = 5x + 3y – 3 = 0
11		g(x,y) = 6x – 4y + 1 = 0
12		g(x,y) = 3x + y +2 = 0
13		g(x,y) = 4x – 2y + 3 = 0
14		g (x,y) = 6x – 4y – 2 = 0
15		g(x,y) = 5x – 3y + 1 = 0
16		g(x,y) = 3x + y – 3 = 0
17		g(x,y) = 4x – 2y + 1 = 0
18		g(x,y) = 5x – 2y + 2 = 0
19		g(x,y) = 6x – 3y – 1 = 0
20		g(x,y) = 3x + 6y – 4 = 0
21		g(x,y) = 2x – 2y + 6 = 0
22		g(x,y) = 3x + y – 1 = 0
23		g(x,y) = 3x – 4 y + 1 = 0
24		g(x,y) = 2x – 2y –1 = 0
25		g(x,y) = 3x – 4 y + 1 = 0
26		g(x,y) = 2x – 2y –1 = 0
27		g(x,y) = 5x + 3y – 3 = 0
28		g(x,y) = 6x – 4y + 1 = 0
29		g(x,y) = 3x + y +2 = 0
30		g(x,y) =4x – 2y + 3 = 0
31		g(x,y) = 6x – 4y – 2 = 0
32		g(x,y) = 5x – 3y + 1 = 0

Например Задание 55: f(x,y)=2x³+xy²+5x²+y²
1 Определение координат стационарных точек

(1)

(2)
Так как из (2) следует, что то

либо либо .

Подставляя оба эти значения в (1), получаем



откуда



при этом Проверка:

;



Таким образом, имеем 4 стационарные точки (результаты указаны в десятичной форме с округлением дробной части до трёх знаков):



.
2 Определение вида стационарных точек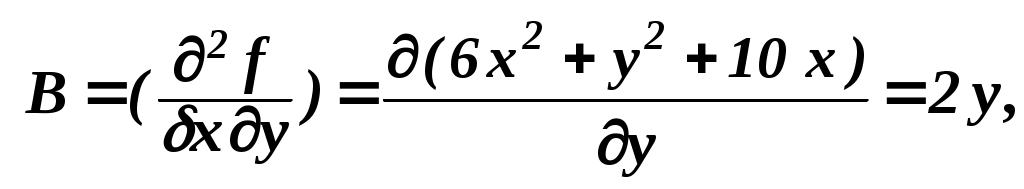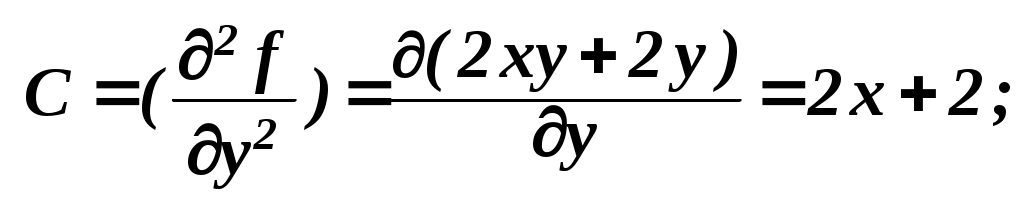







в точке (0,0): Здесь ; значит является точкой экстремума, а так как А и С положительны, то точкой минимума;

значение f(0,0) = 2x³+xy²+5x²+y² = 0;

в точке (–1,667;0):

,



Так как

,

то рассматриваемая точка является точкой экстремума, а так как А и С отрицательны, то точкой максимума;

Значение функции

f( ;0)=2x³+xy²+5x²+y² =2 +5 = 4,630;

в точке (-1,2): Так как в рассматриваемой точке нет экстремума;

значение f(–1,2) = 2x³+xy²+5x²+y² = 3;

в точке (–1,–2): Так как в рассматриваемой точке нет экстремума;

значение f(–1, –2) = 2x³+xy²+5x²+y² = 3.