окружность. Окружность. Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
|
Окружность, которая касается стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью треугольника. На рисунке 146 изображен треугольник АВС и три его вневписанные окружности с центрами 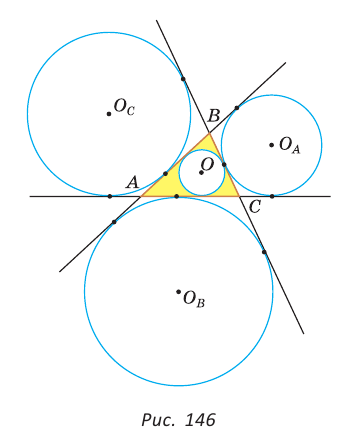 Вневписанные окружности обладают рядом интересных свойств: 1. Центры вписанной и вневписанной окружностей лежат на биссектрисе соответствующего внутреннего угла треугольника. 2. 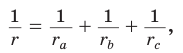 где — радиус вписанной окружности треугольника, где — радиус вписанной окружности треугольника,3. Попробуйте доказать некоторые из этих свойств. 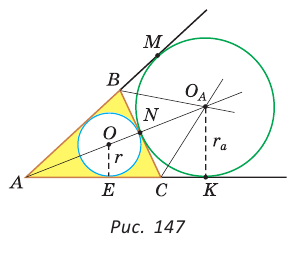 Найдем радиус вневписанной окружности треугольника АВС со сторонами а, b и с (рис. 147). Для этого проведем радиусы 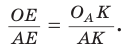 Так как Так как 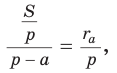 откуда откуда  Пример: Вычислим, используя данную формулу, радиус вневписанной окружности прямоугольного треугольника с катетами 3 и 4, которая касается гипотенузы: 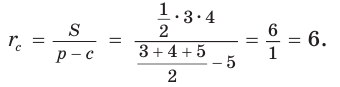 Описанная и вписанная окружности треугольника Определение. Окружность называется описанной около треугольника, если она проходит через все его вершины.  На рисунке 90 изображена окружность с радиусом R и центром Так как ОА = ОВ = ОС = R, то центр описанной окружности равноудален от вершин треугольника. Вместо слов «окружность, описанная около треугольника АВС», также говорят «окружность, описанная вокруг треугольника АВС», или «описанная окружность треугольника АВС». Теорема (об окружности, описанной около треугольника). Около любого треугольника можно описать окружность, причем только одну, ее центр находится в точке пересечения серединных перпендикуляров к сторонам треугольника.  Доказательство: Рассмотрим произвольный треугольник АВС (рис. 91). Пусть О — точка пересечения серединных перпендикуляров к его сторонам. Проведем отрезки ОА, ОВ и ОС. По свойству серединного перпендикуляра ОА = ОС, ОС = ОВ. Так как точка О равноудалена от всех вершин треугольника АВС, то окружность с центром в точке О и радиусом ОА проходит через все вершины треугольника АВС, т. е. является его описанной окружностью. Единственность описанной окружности докажите самостоятельно. Замечание. Так как все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке, то для нахождения центра описанной окружности достаточно построить точку пересечения любых двух из них. Определение. Окружность называется вписанной в треугольник, если она касается всех его сторон. 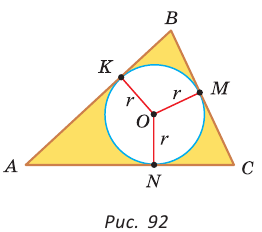 На рисунке 92 изображена окружность с центром О и радиусом вписанная в треугольник АВС; К, М и N — точки ее касания со сторонами треугольника АВС. Так как Вместо слов «окружность, вписанная в треугольник АВС», также говорят «вписанная окружность треугольника АВС». Теорема (об окружности, вписанной в треугольник). В любой треугольник можно вписать окружность, причем только одну, ее центр находится в точке пересечения биссектрис треугольника.  Доказательство: Рассмотрим произвольный треугольник АВС (рис. 93). Пусть О — точка пересечения его биссектрис. Проведем из точки О перпендикуляры ОК, ОМ и ON соответственно к сторонам АВ, ВС и АС. По свойству биссектрисы угла ОК = ON, ON = ОМ. Окружность с центром в точке О и радиусом ОК будет проходить через точки К, М и N и касаться сторон АВ, ВС и АС в указанных точках по признаку касательной. Следовательно, эта окружность является вписанной в треугольник АВС. Единственность вписанной окружности докажите самостоятельно. Замечание. Так как все три биссектрисы треугольника пересекаются в одной точке, то для нахождения центра вписанной окружности достаточно построить точку пересечения любых двух из них. Теорема. Площадь треугольника можно найти по формуле 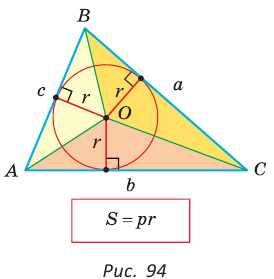 Доказательство: Пусть дан треугольник АВС со сторонами  Теорема доказана. Следствие: Радиус окружности, вписанной в треугольник, можно найти по формуле 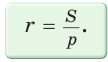 Одной из важнейших задач данной темы является задача нахождения радиуса описанной и радиуса вписанной окружностей данного треугольника. Пример: Найти радиус окружности, описанной около равнобедренного треугольника АВС, у которого АВ = ВС = 26 см, высота ВК = 24 см (рис. 95). 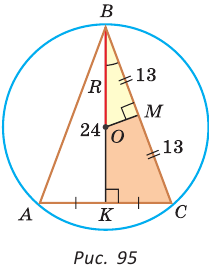 Решение: Способ 1 (метод подобия). Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. Проведем серединные перпендикуляры к сторонам АС и ВС, которые пересекутся в точке О — центре описанной окружности. Так как в равнобедренном треугольнике высота, проведенная к основанию, является медианой, то ВК — серединный перпендикуляр к стороне АС. Пусть МО — серединный перпендикуляр к стороне ВС. Тогда ВМ = 13 см, ВО = R -— искомый радиус. Поскольку 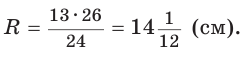 Способ 2 (тригонометрический метод). Из 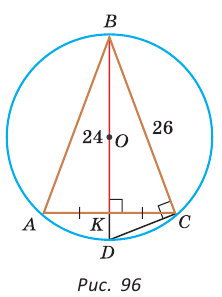 Способ 3* (среднее пропорциональное). Продлим высоту ВК до пересечения с описанной окружностью в точке D (рис. 96). Так как центр описанной окружности равнобедренного треугольника лежит на прямой ВК (см. способ 1), то BD = 2R — диаметр данной окружности. В прямоугольном треугольнике BCD Ответ:  см. см.Замечание. Из решения ключевой задачи 1 следует свойство: «Центр окружности, описанной около равнобедренного треугольника, лежит на его высоте, проведенной к основанию, или на ее продолжении». Верно и обратное утверждение: «Если центр окружности, описанной около треугольника, лежит на высоте треугольника или на ее продолжении, то этот треугольник равнобедренный». Обратное утверждение докажите самостоятельно. Полезно запомнить! Если в ключевой задаче 1 боковую сторону обозначить 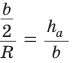 . .Отсюда следует удобная формула для нахождения радиуса окружности, описанной около равнобедренного треугольника:  Пример: Найти радиус окружности, вписанной в равнобедренный треугольник АВС, у которого АВ = ВС = 10 см, АС = 12 см.  Решение: Способ 1 (метод подобия). Центр вписанной окружности находится в точке пересечения биссектрис треугольника. Проведем в треугольнике АВС биссектрисы из вершин В и С, которые пересекутся в точке О — центре вписанной окружности (рис. 97). Биссектриса ВМ, проведенная к основанию равнобедренного треугольника АВС, будет его высотой и медианой, луч СО — биссектриса угла С, Способ 2 (тригонометрический метод). Из 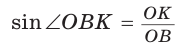 , из , из  откуда откуда Способ 3 (свойство биссектрисы треугольника). СО — биссектриса Способ 4 (формула 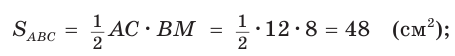 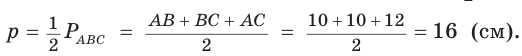 Из формулы площади треугольника Из формулы площади треугольника 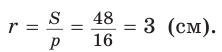 Ответ: 3 см. Замечание. Из решения ключевой задачи 2 следует свойство: «Центр окружности, вписанной в равнобедренный треугольник, лежит на его высоте, проведенной к основанию». Верно и обратное утверждение: «Если центр окружности, вписанной в треугольник, лежит на высоте треугольника, то этот треугольник равнобедренный». Обратное утверждение докажите самостоятельно. |
