Задачи по теме энтропия. Теория ин-фо. Теория ин-фо. Основные свойства энтропии

• Название: Основные свойства энтропии
• Анкор: Задачи по теме энтропия. Теория ин-фо
• Дата: 23.11.2022
• Размер: 118.81 Kb.
• Имя файла: Теория ин-фо.docx
• Тип: Лабораторная работа; #808823

Лабораторная работа № 5

Тема: Основные свойства энтропии

Цель работы: Решение задач по основным свойствам энтропии
Задание: Условная энтропия. Энтропия объединения. Понятие избыточности информации. Оценка потерь информации. Дифференциальная энтропия.
1. Задано распределение вероятностей случайной дискретной двумерной величины. Распределение вероятностей случайной дискретной двумерной величины. Заданная на рисунке 1 - Распределение вероятностей.


Рисунок 1 - Распределение вероятностей
Найти законы распределения случайных величин X, Y, X+Y и проверить в каждом случае выполнение равенства полной суммы вероятностей единице.

Нахождение распределение случайной величины X. Случайная величина X может принимать значения x1=3, x2=10, x3=12. Для нахождения распределения используется теорема 1. Вероятность суммы конечного числа независимых событий вычисляется по формуле на рисунке 2 – Теорема 1


Рисунок 2 – Теорема 1
Находится сумма вероятности Х. Для получения закона, распределения величины X: Р(х1) = 0,17 + 0,10 = 0,27; Р(х2) = 0,13 + 0,30 = 0,43; Р(х3) = 0,25 + 0,05 = 0,3. Проверка выполнение равенства полной суммы вероятностей: 0,27+0,43+0 ,3= 1

Аналогично находится закон распределения величины У: Р(у1) = 0,55; Р(у1) = 0,45

Нахождения закона распределения случайной величины X+Y. Для этого следует найти значения может принимать данная величина. Для этого происходит попарное сложение значения величин X и Y. Получим следующие значения: 7, 8; 14,15; 16, 17. После, отбрасываются совпавшие величины, получим, что случайная величина X+Y может принимать значения z1= 7, z2 = 8, z3= 14, z4 = 15, z5= 16, z6 = 17.

Найдем P(zn). Если значение идентичные z находятся следующим образом на рисунке 2 - P(zn).

Рисунок 2 - P(zn).
Следовательно: Р(z1)= 0,17, Р(z2) = 0,10, z3= 0,13, z4 = 0,30, z5= 0,25, z6 = 0,05. Значит закон распределения величины Z имеет вид таблицы 1 - распределения величины Z
Таблица 1 - распределения величины Z

Х+У	7	8	14	15	16	17
Р	0,17	0,10	0,13	0,30	0,25	0,05

Выполнение неравенства полной суммы вероятностей: 0,17 + 0,10 + 0,13 + 0,30 + 0,25 + 0,05 = 1
2. Задана случайная дискретная двумерная величина (X,Y). На рисунок 3 - Случайная дискретная двумерная величина

Рисунок 3 - Случайная дискретная двумерная величина
Найти: безусловные законы распределения составляющих; условный закон распределения составляющей Х при условии, что составляющая Y приняла значение y₁ = 0,4; условный закон распределения составляющей Y при условии, что составляющая Х приняла значение х₂ = 5

Безусловные законы распределения составляющих образуется складываем вероятности по строкам и столбцам, отображенных на таблице 1 - Безусловные законы распределения составляющих
Таблица 2 - Случайная дискретная двумерная величина

x	2	5	8	у	0,4	0,8
p	0,2	0,42	0,38	p	0,8	0,2

Поиск условного закона распределения х при у₁ = 0,4.
P(х=0,15 | у1 = 0,4) = = = 0,06

P(х=0,30 | у1 = 0,4) = = = 0,15

P(х=0,35 | у1 = 0,4) = = = 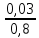0,03
Поиск условного закона распределения У при х₂ = 5.
P(х=0,4 | х2 = 5) = = = 0,7

P(х=0,8 | х2 = 5) = = = 0,2
3. Закон распределения вероятностей системы, объединяющей зависимые источники информации X и Y, задан с помощью рисунка таблицы. Рисунок 4. - Зависимые источники X и Y. Определить энтропии Н(Х), H(Y), HX(Y), H(X,Y).

Y X	y1	y2	y3
x1	0,4	0,1	0
x2	0	0,2	0,1
x3	0	0	0,2

Рисунок 4. - Зависимые источники X и Y
Вычисление безусловных вероятностей Р(x_i) и Р(y_j). Вероятности возможных значений Х находится путем сложения по строкам: P(x₁) = 0,5; P(x₂) = 0,3; P(x₃) = 0,2. Сложение вероятностей по столбцам дает вероятности возможных значений Y: P(y₁) = 0,4; P(y₂) = 0,3; P(y₃) = 0,3.

Расчёт энтропии источника информации Х и У ведется по формуле (1)


(1)
Условная энтропия источника информации Y при условии, что сообщения источника Х известны рассчитывается по формуле 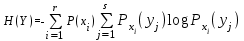(2).
(2)
Так как условная вероятность события y_j при условии выполнения события х_i принимается по определению рассчитывается по формуле (3).
(3)
Поэтому найдем условные вероятности возможных значений Y при условии, что составляющая Х приняла значение x_n:





Поэтому: H_X(Y) = - [0,5 (0,8 log 0,8 + 0,2 log 0,2) + 0,3 (0,67 log 0,67 + 0,33 log 0,33) + 0,2 (1 log 1)] = 0,635

Аналогично, условная энтропия источника информации Х при условии, что сообщения источника Y известны.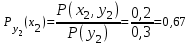

:







Общая энтропия зависимых источников информации Х и Y. Отображена на формуле (4).

4

Проверим результат по формуле:

Н(Х,Y) = H(X) +H_X(Y) = 1,485 + 0,635 = 2,12 бит

Н(Х,Y) = H(Y) +H_Y(X) = 1,57 + 0,55 = 2,12 бит

4 Известны энтропии двух зависимых источников Н(Х) = 5бит; Н(Y) = 10бит. Определить, в каких пределах будет изменяться условная энтропия Н_Х(Y) в максимально возможных пределах.

При отсутствии взаимосвязи между источниками информации на рисунке 5 - отсутствия взаимосвязи. Если источники информации независимы: Н(Y) = 10 бит, H(X) = 5 бит, следовательно Н(X,Y) = 15 бит. То есть, когда источники независимы то принимают максимальное значение.

Рисунок 5 - отсутствия взаимосвязи
По мере увеличения взаимосвязи источников значение будет уменьшаться. Рисунок 6 - Частичная зависимость

Рисунок 6 - Частичная зависимость
При полной зависимости один из источников не вносит никакой информации, Н_Y(X) = 0, следовательно, Н(X,Y) = Н_Х(Y) . Рисунок 7 – Полная зависимость

Рисунок 7 – Полная зависимость
При этом Н_Х(Y) = Н(Y) - Н(Х) = 10 - 5 = 5 бит. Поэтому Н_Х(Y) будет изменяться от 10 бит до 5 бит при максимально возможном изменении Н_y(Х) от 5 бит до 0 бит.