Документ Microsoft Word (5). При представлении чисел с фиксированной точкой
 Скачать 117.3 Kb. Скачать 117.3 Kb.
|
|
Системы счисления и представление информации в ЭВМ Представление чисел в ЭВМ В цифровых ЭВМ числовая информация представляется в двух формах: с фиксированной точкой (естественная форма); с плавающей точкой (экспоненциальная форма). При представлении чисел с фиксированной точкой подразумевается, что положение точки, разделяющей число на целую и дробную части, неизменно для всех чисел. Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому не всегда приемлема при вычислениях. В современных ЭВМ естественная форма используется, например, для представления целых чисел (дробная часть числа всегда отсутствует), денежных сумм (дробная часть всегда составляет четыре знака). Представление с плавающей точкой любого числа N в общем виде описывается следующей формулой: N = ± M × p±k, (1) где ±M – мантисса (дробная часть) числа; p – основание системы счисления; ±k – порядок (целое число), при этом положительный знак мантиссы и порядка может опускаться, а при указании порядка в десятичной системе принято использовать символ Е. Например, десятичное число с фиксированной точкой 123,45 может быть представлено в форме с плавающей точкой как 0,12345 × 100, или, как это принято, 1.2345Е+02. Такая форма представления имеет огромный диапазон отображения чисел и является основной в современных ЭВМ. Исходные данные в ЭВМ хранятся в виде двоичных чисел, т.е. записываются в виде последовательности нулей и единиц. В памяти ЭВМ одна двоичная цифра записывается в один двоичный разряд, называемый битом. За единицу представления данных в цифровых ЭВМ принят байт – восемь бит, поэтому число разрядов ячеек памяти всегда кратно восьми, а данные имеют байтовую структуру, то есть состоят из определенного числа байтов. Более крупные единицы измерения данных образуются добавлением префиксов кило-, мега-, гига-, тера-. Для представления положительных и отрицательных чисел в машинах используются специальные коды: прямой, обратный и дополнительный. Причем два последних позволяют заменить неудобную для ЭВМ операцию вычитания на операцию сложения с отрицательным числом. Дополнительный код обеспечивает более быстрое выполнение операций при помощи сумматора, поэтому в ЭВМ применяется чаще именно он. Рассмотрим правила кодирования на примере целых чисел. Для перевода числа в прямой код знак числа опускается, а в старший (знаковый) разряд ставится 0, если число положительное, и 1 – если число отрицательное. Младшие разряды кода являются двоичным представлением модуля числа. Оставшиеся разряды кода заполняются нулями. Отметим, что перевод положительных чисел в прямой, обратный и дополнительный код не изменяет изображения этих чисел (таблица 1). Для перевода отрицательного числа в обратный код необходимо все, кроме знакового, разряды прямого кода проинвертировать (заменить нули на единицы, а единицы на нули). Для перевода отрицательного числа в дополнительный код необходимо к младшему разряду его обратного кода прибавить единицу. Перевод отрицательного числа из дополнительного кода в прямой осуществляется в обратной последовательности: сначала вычитается единица, затем инвертируются разряды. Напомним, что положительное число (0 в старшем разряде) обратному переводу не подвергается, поскольку имеет одинаковую запись как в прямом коде, так и в дополнительном. Таблица 1 – Примеры представления целых чисел в шестнадцатиразрядных двоичных кодах
Примеры записи чисел в форме с плавающей точкой 1) Число 2 в нормальной форме записывается следующим образом: 210 = 22×(1/2) = 1010×0.12. Соответствующая запись числа 2 в 32-разрядной ячейке памяти машины такова: 01 000 010 100 000 . . . 000. 2) –310 = –22×(3/4) = –1010×0.112. Следовательно, число –3 запишется в 32-разрядной ячейке, как: 11 000 010 110 000 . . . 000. 3) 3/64 = 2–4×(3/4)=10–100×0.112. Запись числа 3/64 в 32-разрядной ячейке памяти ЭВМ: 00 111 100 110 000 . . . 000. 4) –(13/4096)=–2–8×(13/16)=–10–1000×0.11012. Исходя из нормальной формы числа –(13/4096), получим следующую запись числа в 32-разрядной ячейке памяти: 10 111 000 110 100 000 . . . 000. Системы счисления и представление информации в ЭВМ Понятие об основных системах счисления Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления. А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами: для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток - нет тока, намагничен - не намагничен и т.п.), а не, например, с десятью, как в десятичной; представление информации посредством только двух состояний надежно и помехоустойчиво; возможно применение аппарата булевой алгебры для выполнения логических преобразований информации; двоичная арифметика намного проще десятичной. Недостаток двоичной системы - быстрый рост числа разрядов, необходимых для записи чисел. Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.  Непозиционными называются такие системы счисления, в которых каждый символ сохраняет свое значение независимо от места его положения в числе. Примером непозиционной системы счисления является римская система, в которой символам I, V, X, L, С, D, М соответствуют числа 1, 5, 10, 50, 100, 500, 1000. Недостатком этой системы является сложность формальных правил записи чисел и выполнения арифметических действий над ними. Система счисления называется позиционной, если значение каждого знака в числе зависит от позиции, которую занимает знак в записи числа. Это значение находится в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону. Примером позиционной системы счисления является десятичная система, используемая в повседневной жизни. Количество различных цифр, употребляемых в позиционной системе, определяет название системы счисления и называется основанием системы счисления. Так, в десятичной системе используются десять цифр (от 0 до 9), основанием этой системы является число десять. В позиционных системах счисления числа записываются в виде последовательности символов: N = an an-1 ... a1 a0, a-1 a-2 ... а-m (р) (2) где N – число; ai – цифры (символы) числа; p – основание системы счисления; n, m – порядковый номер разряда для целой (n) и дробной (m) частей числа соответственно. В этой последовательности запятая отделяет целую часть числа от дробной (коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях). Значение числа, записанного в виде (1), может быть найдено по следующей формуле: N = an·pn+an-1·pn-1+ ... +a0·p0+a-1·p-1+a-2·p-2+ ...+а-m·p-m . (3) В десятичной системе счисления мы производим вычисления по формуле (2) практически не задумываясь. Возьмем для примера десятичное число 123,45: 2 1 0 -1 -2 1 2 3, 4 5 (10) = 1·102+2·101+3·100+4·10-1+5·10-2 = 100+20+3+0,4+0,05 Основание системы счисления, в которой представлено число, будем указывать в виде нижнего индекса в скобках. Помимо десятичной, в ЭВМ применяются и другие позиционные системы счисления: двоичная, восьмеричная, шестнадцатеричная. Двоичная система счисления Используется две цифры: 0 и 1. Особая значимость двоичной системы счисления в информатике определяется тем, что внутреннее представление любой информации в компьютере является двоичным кодом. Примеры представления чисел в двоичной системе счисления представлены в таблице 2. Восьмеричная система счисления Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употреблялась в ЭВМ первого и второго поколений как вспомогательная для записи адресов и данных в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (Таблица 1). Триада получается путем добавления, при необходимости, незначащих нулей. Шестнадцатеричная система счисления Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр - латинскими буквами: 10 - A, 11 - B, 12 - C, 13 - D, 14 - E, 15 - F. Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада, или полубайт) (Таблица 2). Таблица 2. – Представление чисел в различных системах счисления
Начало формы Далее Конец формы ◄ Задачи для самостоятельной работы Начало формы  Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы. Пример 1. Перевести в десятичную систему счисления:а) 10101101,101(2) ; б) 703,04(8) ; в) B2E,4(16) . Решение: а) 10101101,101(2) = 1·27 + 0·26 + 1·25 + 0·24 + 1·23 + 1·22 + 0·21 + 1·20 + 1·2-1 + + 0·2-2 + 1·2-3 = 173,625(10) б) 703,04(8) = 7 · 82 + 0 · 81 + 3 · 80+ 0 · 8-1 + 4 · 8-2 = 451,0625(10) в) B2E,4(16) = 11 · 162 + 2 · 161 + 14 · 160 + 4 · 16-1 = 2862,25(10) Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное, меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего. Пример 2. а) Перевести 181(10) в восьмеричную систему счисления; б) Перевести 622(10) в шестнадцатеричную систему счисления. Решение: а)
Результат: 181(10) = 265(8) б)
Результат: 622(10) = 26E(16) Перевод правильных дробей из десятичной системы счисления в недесятичную. Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого. Пример 3. Перевести 0,3125(10) в восьмеричную систему счисления. Решение:
Результат: 0,3125(10) = 0,24(8) Замечание. Конечной десятичной дроби может соответствовать бесконечная (периодическая) дробь в недесятичной системе счисления. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности. Пример 4. Перевести 0,65(10) в двоичную систему счисления с точностью до 6 знаков после запятой. Решение:
Результат: 0,65(10) ≈ 0,101001 (2) Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную. Пример 5. Перевести 23,125(10) в двоичную систему счисления Решение: 1) Переведем целую часть:
2) Переведем дробную часть:
Таким образом: 0,125(10) = 0,001(2); 23(10) = 101112. Результат: 23,125(10) = 10111,001(2). Необходимо отметить, что целые числа остаются целыми, а правильные дроби - дробями в любой системе счисления. Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) – для восьмеричной системы счисления или четырехразрядным двоичным числом (тетрадой) – для шестнадцатеричной системы счисления (таблица 1), после чего отбрасывают незначащие нули в старших и младших разрядах. Пример 6. Перевести в двоичную систему счисления: а) 305,4(8); б) 7B2,E(16) . Решение: а)
б)
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от десятичной точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой (таблица 2). Пример 7. Перевести а) 1101111001,1101(2) в восьмеричную систему счисления; б) 11111111011,100111(2) в шестнадцатеричную систему счисления. Решение: а)
б)
Перевод из восьмеричной в шестнадцатеричную систему и обратно удобно осуществлять через двоичную систему с помощью триад и тетрад. Пример 8. Перевести 175,24(8) в шестнадцатеричную систему счисления. Решение:
Примеры перевода Для изображения десятичных дробей используется подобная формула разложения по степеням основания. Пример 9. Перевести в десятичную систему счисления: а) 110,0012 ; б) A,B16. Решение: а) 110,0012 = 1 x 22 + 1 x 21 + 0 x 20 + 0 x 2-1 + 0 x 2-2 + 1 x 2-3 = 6,12510 ; б) A,B16 = A x 160 + B x 16-1 = 10 x 1 + 11 x 0,0625 = 10,687510 . Процедура перевода десятичных чисел в р-ную систему счисления: перевести отдельно целую часть числа х, для чего последовательно делить сперва целую часть [х]10 , а затем все частные (получаемые при делении) на р до тех пор, пока не получим в очередном частном число меньшее р; изображение [х]p получается последовательным приписыванием к последнему частному остатков от деления – от последнего до первого; перевести отдельно дробную часть (мантиссу) числа, то есть {x}10 , для чего последовательно умножать сперва исходную мантиссу, а затем мантиссы получаемых чисел на р до тех пор, пока не получим мантиссу, равную нулю, или нужное количество цифр в {х}p ; изображение {х}p получается приписыванием к целой части первого произведения второй такой же цифры и т.д., до последней цифры целой части; результат будет иметь вид (х)р = [х]p, {х}p . Пример 10. Перевести в указанную систему счисления: а) 12,810 = ?2 ; б) 29,2510 = ?8 ; 79,2610 = ?16 . Решение: а) 1. Переводим целую часть: 1210 =11002; 2. переводим дробную часть: 0,8 x 2 = 1,6; 0,6 x 2 = 1,2; 0,2 x 2 = 0,4; 0,4 x 2 = 0,8; 0,810 = 0,1100110...2 ; 3. результат перевода: 12,810 = 1100,1100110011...2 . б) 1. Переводим целую часть: 2910 = 358 ; 2. переводим дробную часть: 0,2510 = 0,28 ; 3. результат перевода: 29,2510 = 35,28 . в) 1. Переводим целую часть: 7910 = 4F16 ; 2. переводим дробную часть: 0,2610 = 0,4016 ; 3. результат перевода: 79,2610 = 4F,416 . При переводе дробной части мы ограничились нахождением двух значащих цифр после запятой, ибо перевод точно сделать невозможно. Для перевода из 2-ной в 8-ную и наоборот, из 2-ной в 16-ную и наоборот, из 8-ной в 16-ную и обратно, используется таблица следующего вида:
При переводе в 8-ную систему или из нее необходимо группировать в тройки биты, а при переводе в 16-ную или из нее – группировать их в четверки битов. Можно добавлять, если нужно, незначащие нули (слева от целой части и справа от мантиссы) или отбрасывать их. Пример 11. Рассмотрим переводы в смешанных системах: Из 2-ной системы в 8-ную (двоично-восьмеричное изображение): 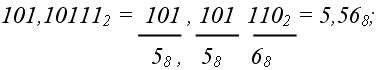 из 8-ной системы в 2–ную (восьмерично-двоичное изображение): 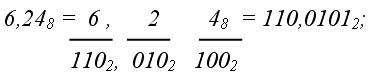 из 2-ной системы в 16-ную (двоично-шестнадцатеричное изображение):  из 16-ной системы в 2-ную (шестнадцатерично-двоичное изображение):  Начало формы Далее Конец формы ◄ Задачи для самостоятельной работы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
