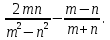ПРИЕМ В 10 КЛАСС
2021 – 2022 учебный год.
Вопросы к собеседованию:
ТЕХНОЛОГИЧЕСКИЙ ПРОФИЛЬ
ФИЗИКА
Механическое движение. Принцип относительности Галилея. Траектория. Путь и перемещение. Скорость. Равномерное прямолинейное движение. График зависимости координаты от времени при равномерном движении. Средняя скорость.
Равноускоренное движение. Ускорение. Перемещение и скорость при равноускоренном движении. График зависимости скорости от времени при равноускоренном движении. Свободное падение.
Движение тела по окружности. Период и частота обращения. Линейная и угловая скорости. Центростремительное ускорение.
Сила. Виды сил. Законы Ньютона.
Закон Всемирного тяготения. Границы применимости закона. Ускорение свободного падения. Первая космическая скорость.
Импульс тела. Импульс силы. Закон сохранения импульса тела. Реактивное движение. Расчет скорости ракеты.
Механическая работа. Мощность. Энергия. Виды энергий.
Момент силы. Плечо. Условие равновесия рычага.
Закон Паскаля. Сообщающиеся сосуды. Свойство и применение сообщающихся сосудов.
Давление жидкости. Сила Архимеда. Условия плавания тел.
Простые механизмы. Рычаг, наклонная плоскость, блоки. КПД простого механизма. Золотое правило механики.
Механические колебания. Виды колебаний. Характеристики колебаний.
Виды маятников. Закон сохранения и превращения энергии при колебательном движении. Резонанс.
Механическая волна. Продольные и поперечные волны. Скорость и длина волны. Звук. Характеристики звука.
Внутренняя энергия. Способы изменения внутренней энергии. Количество теплоты. Расчет количества теплоты при нагревании тела. Теплопроводность.
Агрегатные состояния вещества (расположение, движение и взаимодействие частиц). Фазовые переходы. График фазовых переходов.
Электрический ток. Характеристики электрического тока. Закон Ома.
Закон прямолинейного распространения света. Образование тени. Закон отражения. Закон преломления. Линза. Построение изображения в линзе.
МАТЕМАТИКА
Билет № 1
Сложение и вычитание обыкновенных дробей с разными знаменателями. Умножение и деление обыкновенных дробей. Основное свойство дроби. Сокращение обыкновенных дробей.
Определение параллельных прямых. Признаки параллельности прямых. Аксиома параллельных прямых. Теоремы об углах, образованных двумя параллельными прямыми и секущей.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, а высота фонаря 4 м?
Найдите значение выражения: 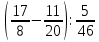 . .
|
Билет № 2
Уравнение и его корни. Линейное уравнение с одной переменной. Алгоритм решения задач с помощью уравнений.
Понятие вектора. Коллинеарные векторы. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число.
Р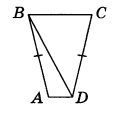 ешите уравнение: ешите уравнение: 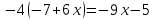 . .
В трапеции ABCD известно, что AB = CD, BDA = 62 и BDC = 42. Найдите ABD.
|
Билет № 3
Степень с натуральным и с целым показателем. Свойства степеней.
Синус, косинус и тангенс острого угла прямоугольного треугольника. Теоремы синусов и косинусов. Решение треугольников.
Решите систему уравнений: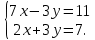
В треугольнике ABC угол С равен 90, AB = 5, 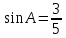 . Найдите AC. . Найдите AC.
|
Билет № 4
Одночлен. Многочлен. Стандартный вид одночлена и многочлена. Сложение и вычитание многочленов. Умножение одночлена на многочлен. Умножение многочлена на многочлен. Привести примеры.
Правильные многоугольники. Окружность, описанная около правильного многоугольника и окружность, вписанная в него. Построение правильных многоугольников.
Решите уравнение: (x + 2)2 = (x − 4)2.
Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах.
|
Билет № 5
Способы разложения многочлена на множители. Формулы сокращённого умножения.
Угол между векторами. Скалярное произведение векторов. Перпендикулярные векторы. Условие перпендикулярности двух векторов. Косинус угла между векторами.
Найдите периметр прямоугольника, если одна из его сторон равна 15, а диагональ равна 17.
Упростите выражение: а) 20 · 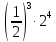 ; б) 7 + 2√5 - √20. ; б) 7 + 2√5 - √20.
|
Билет № 6
Рациональная дробь. Сокращение дробей. Сложение, вычитание, умножение и деление рациональных дробей.
Центральные и вписанные углы. Свойства вписанных углов. Теорема о произведении отрезков пересекающихся хорд.
Упростите выражение: а) 35 · 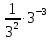 ; б) 5 - 3√7 + √63. ; б) 5 - 3√7 + √63.
Диагонали ромба ABCD пересекаются в точке O и равны 9 и 40. Найдите длину вектора 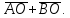
|
Билет № 7
Прямоугольная система координат на плоскости. Понятие функции. Способы задания функции. График функции. Функция у=кх и ее график. Линейная функция и её график. Привести примеры.
Окружность, круг. Длина окружности. Площадь круга.
Дан прямоугольный треугольник АВС, С = 90°, АВ = 13, АС = 5. Найдите косинусугла В.
Найдите значение выражения: 0,8 (-10)4 + 3 (-10)3 + 78.
|
Билет № 8
Система уравнений с двумя неизвестными. Способы решения систем уравнений.Примеры.Алгоритм решения задач с помощью системы уравнений.
Треугольник. Признаки равенства треугольников. Медианы, биссектрисы и высоты треугольника.
Р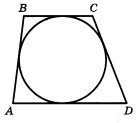 ешитеуравнение: 3х2 + 5х - 2 = 0. ешитеуравнение: 3х2 + 5х - 2 = 0.
Трапеция ABCD с основаниями AD и BC описана около окружности, AB = 9, BC = 7, CD = 11. Найдите AB.
|
Билет № 9
Линейные неравенства с одним неизвестным. Система неравенств с одним неизвестным. Числовые промежутки. Примеры.
Теорема Пифагора. Теорема, обратная теореме Пифагора. Пропорциональные отрезки в прямоугольном треугольнике.
В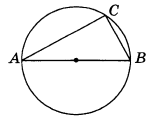 ыполните действия: ыполните действия: 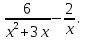
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 33.
|
Билет № 10
Понятие арифметического квадратного корня и его свойства.
Простейшие задачи в координатах: координаты середины отрезка, вычисление длины вектора по его координатам, расстояние между двумя точками.
Р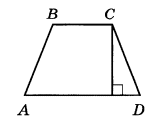 ешите систему уравнений: ешите систему уравнений: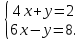
Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 14 и 19. Найдите длину основания BC.
|
Билет № 11
Квадратное уравнения и его корни. Неполные квадратные уравнения.Решение квадратных уравнений. Разложение квадратного трехчлена на множители.
Подобные треугольники. Признаки подобия треугольников. Отношение площадей подобных треугольников.
Упростите выражение: 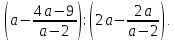
Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 132.
|
Билет № 12
Приведённое квадратное уравнение. Теорема Виета.Алгоритм решения систем, содержащих уравнение второй степени.
Равнобедренный треугольник, его свойства и признаки.
Сократите дробь: 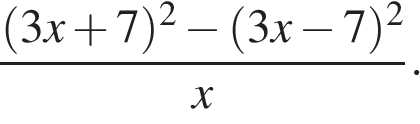
Найдите сторону квадрата, вписанного в окружность радиуса 182.
|
Билет № 13
Определение квадратичной функции. Функции у=х2, у=ах2, у=ax2+bx+c. Построение графика, свойства.
Понятие площади многоугольника.Основные свойства площадей. Площади прямоугольника, параллелограмма, треугольника, трапеции.
На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
В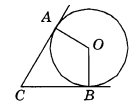 угол С величиной 79 вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. угол С величиной 79 вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB.
|
Билет № 14
Квадратное неравенство и его решение. Решение квадратного неравенства с помощью графика квадратичной функции. Метод интервалов. Примеры.
Вписанная и описанная окружности. При каком условии в окружность можно вписать четырёхугольник. В какой четырёхугольник можно вписать окружность?
Гипотенуза прямоугольного треугольника равна 29. Один из катетов равен 20. Найдите площадь треугольника.
Решите неравенство: x2 + 9x + 20< 0
|
Билет № 15
Целые и дробно-рациональные уравнения. Способы их решения. Примеры.
Прямоугольный треугольник. Свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников.
Решите неравенство: 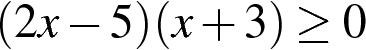
Найдите площадь ромба, если его стороны равны 6, а один из углов равен 150.
|
Билет № 16
Функция y=k/x, ее график и свойства. Привести пример.
Трапеция. Средняя линия трапеции. Виды трапеций. Свойства и признаки равнобедренной трапеции.
Выполните действия: 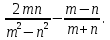
Найдите площадь прямоугольника, если его периметр равен 52, а отношение соседних сторон равно 4 : 9.
|
Билет № 17
Арифметическая прогрессия. Формула n-го члена арифметической прогрессии. Формула суммы n первых членов арифметической прогрессии.
Параллелограмм, его свойства и признаки. Прямоугольник, ромб, квадрат, их свойства.
Расположите в порядке возрастания: √6; 2√3; 3√2; √5.
Найдите углы равнобедренной трапеции, если сумма двух углов этой трапеции равна 220.
|
Билет № 18
Геометрическая прогрессия. Формула n-го члена геометрическойпрогрессии. Формула суммы n первых членов геометрической прогрессии.
Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Уравнение окружности.
Решитеуравнение: 5х2 – 16х + 3 = 0.
Угол A четырёхугольника ABCD, вписанного в окружность, равна 46. Найдите угол С этого четырёхугольника.
|
ИНФОРМАТИКА
1.
В одной из кодировок UTF-32 каждый символ кодируется 32 битами. Петя написал текст (в нём нет лишних пробелов):
«Ель, кедр, сосна, кипарис, лиственница, можжевельник — хвойные растения».
Ученик вычеркнул из списка название одного из растений. Заодно он вычеркнул ставшие лишними запятые и пробелы — два пробела не должны идти подряд.
При этом размер нового предложения в данной кодировке оказался на 20 байт меньше, чем размер исходного предложения. Напишите в ответе вычеркнутое название хвойного растения.
2.
Сообщение было зашифровано кодом. Использовались только буквы, приведённые в таблице:
А
|
Б
|
В
|
Г
|
Д
|
Е
|
..o..
|
.o..o
|
.oo.o
|
.oooo
|
...o.
|
.o.oo
| |
 Скачать 203.02 Kb.
Скачать 203.02 Kb.
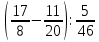 .
. ешите уравнение:
ешите уравнение: 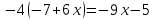 .
.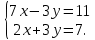
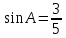 . Найдите AC.
. Найдите AC.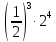 ; б) 7 + 2√5 - √20.
; б) 7 + 2√5 - √20.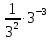 ; б) 5 - 3√7 + √63.
; б) 5 - 3√7 + √63.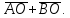
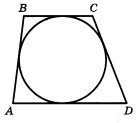 ешитеуравнение: 3х2 + 5х - 2 = 0.
ешитеуравнение: 3х2 + 5х - 2 = 0. ыполните действия:
ыполните действия: 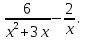
 ешите систему уравнений:
ешите систему уравнений: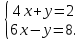
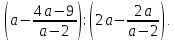
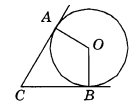 угол С величиной 79 вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB.
угол С величиной 79 вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB.