Ответы на экз вопр по АЗЭЭ. Решение оптимизационными задачами

• Название: Решение оптимизационными задачами
• Дата: 09.02.2021
• Размер: 55.96 Kb.
• Имя файла: Ответы на экз вопр по АЗЭЭ.docx
• Тип: Решение; #175212

1. 
   Оптимизационные задачи в энергетике. Критерии оптимальности
   

При проектировании и эксплуатации технических систем постоянно приходится решать задачи поиска наилучшего решения из некоторого множества допустимых решений. Такое решение называют оптимальным, процесс поиска такого решения - оптимизацией, а задачи, в которых ищется такое решение - оптимизационнымизадачами.

Формулировка любой технической задачи должна быть переведена на формальный математический язык, т.е. записана с помощью определенных математических выражений. Будущий специалист должен знать основы математического моделирования и уметь составлять математические модели оптимизационныхзадач.

Для конкретной оптимизационной задачи не разрабатывается специальный метод решения. Существуют математические методы, предназначенные для решения любых оптимизационных задач - методы математического программирования. Будущий специалист должен знать эти методы математического программирования и уметь выбрать целесообразный метод для решения конкретной техническойзадачи.

Решение задач небольшой размерности можно выполнить традиционными вычислениями с помощью калькулятора. Решение же реальных задач, размерность которых может быть достаточно большой, возможно лишь с помощью персонального компьютера.

Cпециалист должен знать программное обеспечение современных персональных компьютеров и уметь пользоваться этим обеспечением.

Показатель, по величине которого оценивают, является ли решение оптимальным, называется критерием оптимальности.  В качестве критерия оптимальности наиболее часто принимается экономический критерий, представляющий собой минимум затрат (финансовых, сырьевых, энергетических, трудовых) на реализацию поставленной задачи. При заданной или ограниченной величине указанных затрат экономический критерий выражается в получении максимальной прибыли.

В электроэнергетике в зависимости от требований поставленной задачи могут приниматься и другие критерии оптимальности, в частности:

критерий надежности электроснабжения; критерий качества электроэнергии;

критерий наименьшего отрицательного воздействия на окружающую среду (экологический критерий).

Решение оптимизационной задачи включает в себя следующие этапы:

• 
  Сбор исходной информации (исходных данных).
  
• 
  Составление математической модели, под которой понимается формализованное математическое описание решаемой задачи.
  
• 
  Выбор метода решения, определяемого видом математической модели.
  
• 
  Выполнение математических вычислений, поручаемое, как правило, компьютеру.
  
• 
  Анализ решения задачи.
  

2. 
   Экстремум функции
   

Целевая функция представляет собой математическую запись критерия оптимальности. При решении оптимизационной задачи ищется экстремум целевой функции, например минимальные затраты или максимальная прибыль. Обобщенная запись целевой функции имеет следующий вид:

Z(х₁, х₂, ... х_n)→ extr,

где х₁, х₂, ... х_n – искомые переменные, значения которых вычисляются в процессе решения задачи; общее количество переменных равно n.

Зависимость между переменными в целевой функции может быть линейной или нелинейной.

Нелинейная целевая функция в заданном диапазоне изменения переменных может иметь один экстремум или несколько экстремумов. В первом случае функция будет одноэкстремальной, во втором – многоэкстремальной.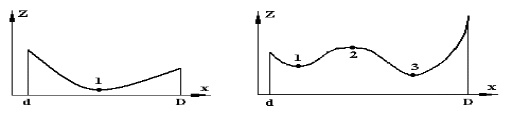

3. 
   
   а) б)
   

Рис. 1.1. Одноэкстремальная (а) и многоэкстремальная (б) функции

3)Математическая модель. Структура мат. Модели

Математическая модель включает в себя:

• 
  Целевую функцию
  
• 
  Ограничения
  
• 
  Граничные условия
  

Целевая функция представляет собой математическую запись критерия оптимальности. При решении оптимизационной задачи ищется экстремум целевой функции, например минимальные затраты или максимальная прибыль. Обобщенная запись целевой функции имеет следующий вид:

Z(х₁, х₂, ... х_n)→ extr,

где х₁, х₂, ... х_n – искомые переменные, значения которых вычисляются в процессе решения задачи; общее количество переменных равно n.

Зависимость между переменными в целевой функции может быть линейной или нелинейной.

Нелинейная целевая функция в заданном диапазоне изменения переменных может иметь один экстремум или несколько экстремумов. В первом случае функция будет одноэкстремальной, во втором – многоэкстремальной.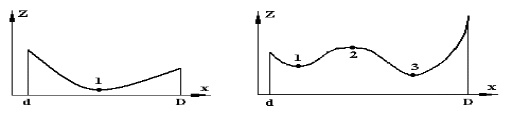


а) б)

Рис. 1.1. Одноэкстремальная (а) и многоэкстремальная (б) функции

Ограничения представляют собой различные технические, экономические, экологические условия, учитываемые при решении задачи. Ограничения представляют собой зависимости между переменными х₁, х₂, ... х_n, задаваемые в форме неравенств или равенств

f₁(х₁, х₂, ... х_n) < b₁;

f₂(х₁, х₂, ... х_n) = b₂; (1.2)

. . . . . . . . . . . . . . . . . . .

f_m(х₁, х₂, ... х_n) > b_m.

Общее количество ограничений равно m. Правые части ограничений, представляющие собой постоянные коэффициенты b_j (j=1, 2, … m), называются свободными членами.

Граничные условия устанавливают диапазон изменения искомых переменных

d_i < х _i < D_i, i=1, 2, … n, (1.3)

где d_i и D_i - соответственно нижняя и верхняя границы диапазона изменения переменной x_i.

4)Анализ решения оптимизационной задачи

В качестве главного средства анализа используется математическая модель, позволяющая выполнить параметрический, структурный и многокритериальный анализ задачи.

Параметрическим называется такой анализ, при котором задача решается многократно при различных значениях некоторого исходного данного (параметра). Оценивается влияние этого параметра на результаты решения.

При структурном анализе многократное решение задачи выполняется при различной структуре ограничений и граничных условий. Оценивается влияние ограничений и граничных условий на результаты решения.

Решение задачи по различным критериям (с различными целевыми функциями) составляет суть многокритериальногоанализа.

Окончательное решение задачи принимается после исследования всех решений, полученных при параметрическом, структурном и многокритериальном анализах.

5)Задачи линейного программирования

Линейной называется зависимость в которой переменные 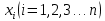входят только в первой степени и с этими степенями выполняют только сложения, вычитания и умножения на постоянный коэффициент.

Если целевая функция Z(х₁, х₂, ...х_n)extr, и система ограничений

f₁(х₁, х₂, ... х_n) <b₁;

f₂(х₁, х₂, ... х_n)=b₂;

. . . . . . . . . . . . . . . . . . .

f_m(х₁, х₂, ... х_n) > b_m.

являются линейно зависимыми от переменных х₁, х ₂, ... х _n, для решения оптимизационной задачи используются методы линейного программирования.

Линейная математическая модель в общем случае имеет следующий вид:

Z =z₁x₁+z₂x₂+...+z_nx_n extr,

a₁₁x₁+a₁₂x₂+...+a_1nx_n< b₁, a₂₁x₁+a₂₂x₂+...+a_2nx_n = b₂,

. . . . . . . . . . . . . . . . . . . . ....

a_m1x₁+a_m2x₂+...+a_mnx_n> b_m,

х_i>0, i = 1, 2, ...n,

где z_i, b_j, a_ji- заданные постоянные величины, i = 1.2,…n; j = 1, 2, ... m. Задача линейного программирования формулируется следующим образом: найти экстремальное значение линейной целевой функции Z

при ограничениях, заданных в форме линейных равенств и (или) неравенств, и граничных условиях, указывающих диапазон изменения переменных.

В реальных оптимизационных задачах ищется или минимум или максимум целевой функции. Методы линейного программирования работают совершенно одинаково, как при поиске минимума целевой функции, так и при поиске ее максимума.

Допустим, что в линейной математической модели (2.1) ищется минимум целевой функции

Z = z₁x₁+z₂x₂+...+z_nx_nmin.

Если по этой же математической модели нужно найти максимум целевой функции Z, то у коэффициентов целевой функции меняются знаки на противоположные и вновь ищется минимум функции Z

Z = - z₁x₁ - z₂x₂ -...- z_nx_nmin.

Таким образом,

min (- z₁x₁- z₂x₂ -…- z_nx_n) = max ( z₁x₁+ z₂x₂+ …+ z_nx_n).

6)Симплекс-метод

Симплекс-метод является универсальным аналитическим методом решения задач линейного программирования. Симплекс - понятие геометрическое, означающее совокупность вершин многомерного тела. Идея симплекс-метода заключается в последовательном переборе решений - в последовательном переходе от одной вершины к другой. Однако этот перебор не хаотичный, а таков, что на каждом шаге решение улучшается.

Метод состоит из двух этапов: на первом этапе ищется допустимое решение; на втором этапе это допустимое решение улучшается до оптимального. 

1этап. Получение допустимого решения. Любое допустимое решение должно удовлетворять системе ограничений-равенств и граничным условиям.

Исходное решение (2.12) удовлетворяет системе ограничений – равенств (2.10). Это решение будет удовлетворять граничным условиям (2.11) в том случае, когда свободные члены b₁>0, b₂>0 и b₃>0. Следовательно, условием получения допустимого решения является неотрицательность свободных членов ограничений- равенств.

Если все b_j>0 (j=1,2,...m), то полученное решение является допустимым. Далее осуществляется переход ко 2-му этапу метода.

Если среди свободных членов есть отрицательные, то выбирается любой из них и соответствующая строка принимается в качестве разрешающей. Базисная переменная, отвечающая разрешающей строке, будет переводиться в разряд свободных.

2этап. Получение оптимального решения. Пусть оптимальному решению соответствует минимальное значение целевой функции Z. Необходимо проверить возможность улучшения полученного на первом этапе допустимого решения, то есть проверить возможность уменьшения значения целевой функции Z. Следовательно, условием получения оптимального решения при минимизации целевой функции является неотрицательность коэффициентов целевой функции z_i'>0.

7)Транспортная задача электроэнергетики

Транспортная задача - это задача отыскания таких путей перевозки продукта от пунктов производства к пунктам потребления, при которых общая стоимость перевозок оказывается минимальной.

Пусть в проектируемой системе электроснабжения имеется i = 1, 2, ... n узлов источников питания и j = 1, 2, ... m узлов потребителей. Мощность каждого из источников - A_i, а мощность каждого из потребителей - B_jединиц мощности (е.м.). Известно взаимное расположение узлов источников и потребителей. Стоимость передачи единицы мощности от i к потребителю j (удельная стоимость) составляет z_ijу.е./е.м.

Общее количество возможных к строительству линий электропередачи, связывающих источники с потребителями, составляет nm. Мощности, передаваемые по этим линиям, являются искомыми переменными , следовательно, количество искомых переменных составляет nm.

Затраты на электрическую сеть равны сумме произведений удельных стоимостей на величины передаваемых мощностей от источников i к потребителям j. Поэтому подлежащая минимизации целевая функция имеет следующий вид:



Электрическая сеть является электрической цепью и для этой сети применимы все законы, в частности 1-й закон Кирхгофа. Для каждого i-го источника питания сумма мощностей, оттекающих по линиям ко всем j=1,2,...m узлам потребителей, равна мощности A_iэтого источника



Для каждого j-го потребителя сумма мощностей, притекающих по линиям от всех i=1,2, ...n источников, равна мощности B_jэтого потребителя



Соотношения (3.2) и (3.2а), представляющие собой балансы мощности в каждом из узлов, являются ограничениями при решении транспортной задачи. Общее количество ограничений равно количеству узлов источников и потребителей n+m.

Количество независимых ограничений составляет (n+m-1). Количество базисных (не равных нулю) переменных равняется количеству независимых ограничений и составляет (n+m-1). Остальные переменные являются свободными (равными нулю). Количество свободных переменных составляет (nm-(n+m-1)).

Каждая базисная переменная x_ijсоответствует присутствию в схеме линии между узлами i и j, поскольку мощность, протекающая между узлами i и j, не равна нулю. Каждая свободная переменная x _ijсоответствует отсутствию в схеме линии между узлами i и j, поскольку мощность, протекающая между узлами i и j, равна нулю.

В рассматриваемой постановке транспортной задачи все искомые мощности х _ij, передаваемые от источников к потребителям, являются неотрицательными. Следовательно, граничные условия имеют вид

x_ij> 0, i=1, 2, ... n; j=1, 2, ... m. (3.3)

8)Мат. Модель транспортной задачи. Ее особенности







Эти выражения представляют собой математическую модель транспортной задачи. Видно, что выражения целевой функции (1) и ограничений (2) и (2а) являются линейными. Следовательно, транспортная задача может быть решена симплекс-методом.

Однако непосредственное применение этого метода к решению транспортной задачи оказывается нецелесообразным. В силу своей универсальности симплекс-метод имеет достаточно сложную вычислительную процедуру и без учета специфических особенностей транспортной задачи ее решение оказывается слишком громоздким.

Особенности транспортной задачи следующие:

• 
  все ограничения имеют форму равенств;
  
• 
  все коэффициенты при переменных в системе ограничений равны плюс единице;
  
• 
  каждая переменная дважды входит в систему ограничений; один раз в балансы узлов источников (2), второй раз в балансы узлов потребителей (2а).
  

С учетом этих особенностей для решения транспортных задач разработаны специальные методы решения, более простые, чем симплекс-метод.

9)Методы решения транспортной задачи

Транспортная задача - это задача отыскания таких путей перевозки продукта от пунктов производства к пунктам потребления, при которых общая стоимость перевозок оказывается минимальной.

Распределительный метод, как и симплекс метод осуществляют за счет перевода одной из базисных переменных в разряд свободных и одной из свободных переменных в разряд базисных. Для получения оптимального решения этот метод является трудоемким. В каждом допустимом решении для каждой свободной переменной необходимо строить циклы и определять изменение целевой функции.

Метод потенциалов является модификацией распределительного метода. В этом методе каждой строке и каждому столбцу транспортной матрицы присваивается свой потенциал: строкам – потенциалы ( столбцам – потенциалы ( . Для каждой базисной переменной сумма потенциалов равна удельной стоимости:



10) Алгоритм решения классической транспортной задачи

Алгоритм решения транспортной задачи.

1. 
   В соответствии с исходными данными составляется транспортная матрица размерностью nm, где n - количество источников питания, m - количество потребителей.
   
2. 
   Находится допустимое решение, например, методом наименьшей удельной стоимости.
   
3. 
   Для допустимого решения каждой i-й строке и каждому j-му столбцу транспортной матрицы присваивается значение потенциала V _i и U _j (i=1,2,...n; j=1,2,...m). Для каждой базисной переменной сумма потенциалов равна удельной стоимости V_i+U_j=z_ij.
   
4. 
   Произвольно задавшись значением одного из потенциалов, по уравнениям V_i+U_j=z_ij, справедливым для базисных переменных, вычисляются значения остальных потенциалов.
   
5. 
   Для всех свободных переменных проверяется соотношение суммы потенциалов с удельной стоимостью. Если для всех свободных переменных V_i+U_j < z_ij, то полученное решение является оптимальным.
   
6. 
   Если имеются свободные переменные, для которых V _i+U_j>z_ij, то выбирается любая из этих свободных переменных и переводится в базис. Для этого строится цикл пересчета (замкнутая ломаная линия), начальная вершина которого лежит в клетке выбранной свободной переменной. Остальные вершины цикла лежат в клетках, соответствующих базисным переменным. Начальной вершине цикла присваивается знак "+", соответствующий увеличению переменной. Далее знаки вершин цикла чередуются. Знаки "+" соответствуют увеличению базисных переменных, знаки "-" - их уменьшению.
   
7. 
   Из отрицательных вершин цикла выбирается вершина с наименьшим значением базисной переменной и на эту величину изменяются все переменные, лежащие в вершинах цикла. В положительных вершинах переменные увеличиваются, в отрицательных - уменьшаются. При этом выбранная свободная переменная становится базисной, а наименьшая по величине базисная переменная в отрицательной вершине цикла становится свободной (равной нулю).
   
8. 
   Для вновь полученного решения вычислительная процедура повторяется, начиная с пункта 3.
   

11)Решение транспортной задачи с учетом пропускной способности линий

Пропускная способность линии электропередачи – это наибольшая активная мощность, которую с учётом всех ограничений (устойчивости, потери на корону, нагрева проводников, контактов) можно передать по линии. Пропускная способность линии электропередачи зависит от напряжения, силы тока и реактивного сопротивления линии.

При проектировании систем электроснабжения часто сталкиваются с задачей ограничения пропускной способности линии. В частности, ограничение передаваемой мощности по существующей линии обусловлено допустимым нагревом ее проводов.

Пусть для линии x_ijмежду источником i и потребителем j передаваемая мощность ограничена величиной S(x_ij<S). Ограничение пропускной способности линии учитывается в транспортной задаче следующим образом.

Столбец j транспортной матрицы, отвечающий потребителю с мощностью B_j, разбивается на два столбца или на два условных потребителя c мощностями В_j'=B_j-S и B_j"=S.

Для переменной между источником i и потребителем B_j' осуществляется блокировка передачи мощности, т.е. для этой переменной принимается очень большой показатель удельной стоимости.

12)Решение транспортной задачи с транзитом мощности

В реальных схемах электрических сетей часто оказывается целесообразной передача мощности через промежуточные (транзитные) узлы. Такими транзитными узлами могут быть как узлы источников питания, так и узлы потребителей. На рис. 3.6 в качестве примера приведены простейшие схемы электрических сетей, поясняющие понятие "транзит мощности".

а) б) в)

Рис. 1. Поясняющие схемы к понятию "транзит мощности"

На рис.1,а показано взаимное расположение узлов источника А1 и потребителей В2 и В3. При классической постановке транспортной задачи оптимальная схема электрической сети будет иметь вид, показанный на рис. 1,б. Очень возможно, что эта схема будет дороже, чем схема, приведенная на рис. 1,в, в которой мощность к потребителю В3 передается через промежуточный (транзитный) узел потребителя В2. Величина транзитной мощности, передаваемой через узел В2, равна мощности потребителя В3, т.е. х22=В3.

Транзитная мощность обозначена переменной с двумя одинаковыми индексами, соответствующими номеру узла, через который она протекает. Можно показать, что транзитным узлом может быть и узел источника питания.

Таким образом, транспортная задача с транзитом мощности является более общей задачей и имеет более широкие возможности по оптимизации схемы электрической сети, чем транспортная задача в классической постановке.

При решении транспортных задач с транзитом мощности с количеством источников n и количеством потребителей m всем узлам схемы присваивается единая нумерация 1, 2, ... (n+m).

Целевая функция представляет собой сумму произведений удельных стоимостей на величины передаваемых мощностей от узла i к узлу j.



Стоимость передачи мощности между узлами i и j не зависит от направления этой мощности, поэтому в рассматриваемой задаче принимается .

Ограничениями в транспортной задаче с транзитом будут балансы мощности во всех узлах. В частности, для узла В₂ схемы рис. 3.6, в баланс мощности запишется в виде х₁₂ = В₂ + х₂₂ или х₁₂ - х₂₂ =В₂.

В общем случае для любого j-го потребителя сумма мощностей, притекающих от всех других узлов, за вычетом транзитной мощности x_jjравна мощности этого потребителя



Аналогично можно записать уравнение баланса мощности для любого i-го источника. Сумма мощностей, оттекающих от i-го источника ко всем другим узлам, за вычетом транзитной мощности x _iiравна мощности этого источника



Из двух последних выражений видно, что транзитная мощность входит в математическую модель транспортной задачи со знаком минус.

Для решения транспортной задачи с транзитом мощности составляется транспортная матрица. Алгоритм решения транспортной задачи с транзитом мощности практически не отличается от алгоритма решения классической транспортной задачи. Отметим отличительные особенности транспортной задачи с транзитом мощности, часть из которых уже упоминалась выше:

• 
  Всем n узлам источников и m узлам потребителей присваивается сквозная нумерация 1, 2, ... (n+m).
  
• 
  Считается, что через любой i-й узел может передаваться транзитная (промежуточная) мощность xii.
  
• 
  Удельные стоимости передачи транзитной мощности zii=0.
  
• 
  Транспортная матрица является квадратной и имеет размерность (n+m)(n+m).
  
• 
  Транзитные переменные x ii входят в решение задачи (в транспортную матрицу) со знаком минус.
  
• 
  Вне зависимости от значения все транзитные переменные считаются базисными.
  

13) Методы нелинейного программирования

Если в математической модели оптимизационной задачи имеются нелинейные зависимости, для решения этой задачи используются методы нелинейного программирования. Большинство реальных оптимизационных задач являются нелинейными.

Как отмечалось в п. 1.2. нелинейная целевая функция может иметь один или несколько экстремумов. Существующие методы нелинейного программирования позволяют найти один экстремум целевой функции. При многоэкстремальной целевой функции диапазон изменения переменных (4.3) разбивается на ряд более узких диапазонов, например

d_i<х_i<a_i, a_i<х_i<b_i, b_i<х_i<D_i, i = 0, 1, 2, ... n, (4.4)

в каждом из которых ищется локальный экстремум целевой функции. Из полученных локальных экстремумов выбирается глобальный экстремум.

Для случая (4.4) оптимизационная задача решается трижды: в диапазоне изменения переменных d_i<х_i< a_i, в диапазоне a_i< х_i<b_iи в диапазоне b_i< х_i< D_i. В результате получаем три локальных экстремума. Из трех локальных экстремумов выбирается глобальный экстремум.

14) Задачи безусловной и условной оптимизации

Наиболее простыми задачами нелинейного программирования являются задачи безусловной оптимизации. В этих задачах ищется абсолютный экстремум целевой функции без ограничений и граничных условий.

В точке экстремума (минимума, максимума) нелинейной функции все ее частные производные равны нулю. Для нахождения экстремума нелинейной функции n переменных необходимо определить ее частные производные по всем переменным и приравнять их к нулю. Решение полученной системы n уравнений c n неизвестными даст значения переменных, при которых достигается экстремум функции.

Точное решение системы уравнений, в общем случае системы нелинейных уравнений, представляет собой достаточно сложную задачу. Поэтому для отыскания экстремума нелинейной функции часто используются другие методы, в частности градиентные методы.

Задачи безусловной минимизации на практике встречаются редко, однако методы их решения являются основой решения большинства практических задач условной оптимизации. В этих задачах ищется условный экстремум целевой функции, т.е. экстремум функции при наличии ограничений и граничных условий.

В большинстве практических оптимизационных задач искомые переменные принимают только положительные или нулевые значения. В этом случае граничные условия имеют вид

х_i>0, i = 0, 1, 2, ... n. (4.5)

15) Градиентные методы

Градиент функции - это вектор который показывает направление и скорость наибольшего изменения функции в рассматриваемой точке. Если в некоторой точке градиент функции , то функция в этой точке не возрастает, и не убывает т.е. эта точка экстремума.

В общем случае сущность градиентных методов сводится к следующему:

Выбирается произвольная точка в ОДЗ, по ее координатам вычисляется целевая функция и градиент этой функции в данной точке:



После этого определяем направления градиента в соответствии с видом экстремума для целевой функции.

После выбора направления начинается пошаговое движение в этом направлении. На каждом шаге координаты изменяются на определенную заданную величину.

Движение в указанном направлении продолжается до тех пор, пока относительное изменение значения целевой функции не станет меньше заданной точности вычислений.



Необходимо понимать, что если меньше длина шага, то тем больше шагов до получения оптимального решения, но при этом точность будет максимальной.

Существуют следующие градиентные методы:

1. 
   Метод покоординатного спуска
   
2. 
   Метод скорейшего спуска
   
3. 
   Метод проектирования градиента
   

16) Задача оптимального распределения активной мощности

В существующей энергосистеме необходимо так распределять активную нагрузку между электростанциями, чтобы затраты на выработку ЭЭ были минимальными. В простейшем случае в ЭС имеются электростанции только одного типа, но могут иметь место электростанции всех трех типов.

Для агрегатов каждой электростанции (ТЭС и АЭС) всегда известны расходные характеристики (зависимости расхода топлива от активной мощности). Эти характеристики имеют линейный характер. В данном случае целевая функция будет представлять собой сумму расходных характеристик. Кроме того, необходимо учитывать баланс мощностей (система ограничений). Граничными условиями являются неотрицательные значения искомых мощностей электростанции.

17) Задача оптимального распределения реактивной мощности в энергосистеме

Большинству потребителей нужна как активная, так и реактивная мощность. Необходимо учитывать, что компенсация реактивной мощности позволяет уменьшить потери активной мощности и улучшить технико-экономические показатели схемы электроснабжения (уменьшить денежные затраты). Но установка компенсаторов также требует денежных затрат. Идеально было бы для каждого потребителя установить собственный компенсатор, но это совершенно не экономично, поэтому обычно устанавливают один компенсатор на несколько потребителей, при этом очень важно выбрать его мощность и место расположения.

18) Задача определения оптимальной мощности КУ

Большинству потребителей нужна как активная, так и реактивная мощность. Необходимо учитывать, что компенсация реактивной мощности позволяет уменьшить потери активной мощности и улучшить технико-экономические показатели схемы электроснабжения (уменьшить денежные затраты). Но установка компенсаторов также требует денежных затрат. Идеально было бы для каждого потребителя установить собственный компенсатор, но это совершенно не экономично, поэтому обычно устанавливают один компенсатор на несколько потребителей, при этом очень важно выбрать его мощность и место расположения.

19) Методы целочисленного программирования. Задачи с двоичными переменными.

При решении достаточно большого количества оптимизационных задач все искомые переменные или их часть должны принимать только значения целых чисел. Математическая модель таких задач аналогична рассмотренным выше линейным и нелинейным моделям и содержит целевую функцию, систему ограничений и граничные условия. Однако система ограничений в задачах с целочисленными переменными дополняется ограничениями типа

х_k – целое, k = 1, 2, … l, (5.1)

где l – количество целочисленных переменных, l < n;

n – общее количество переменных.

Оптимизационные задачи, в которых искомые переменные или их часть должны быть целыми числами, решаются методами целочисленного программирования.

Введение дополнительных ограничений по целочисленности переменных существенно увеличивает объем вычислений и усложняет вычислительную процедуру при поиске оптимального решения. Однако в заданном диапазоне изменения переменной целочисленная переменная имеет меньшее количество значений, чем непрерывная переменная. В частности, в диапазоне 0 < x < 3 целочисленная переменная х имеет четыре значения (х = 0, 1, 2, 3), а непрерывная переменная - бесконечное количество значений.

Попытка решить целочисленную оптимизационную задачу методом полного перебора значений переменных приводит к очень большому объему вычислений. Другая попытка решения целочисленной задачи заключается в решении этой задачи без наложения ограничений вида. В этом случае решается обычная задача с непрерывными переменными, а полученные непрерывные переменные округляются до целых чисел.

Существуют различные методы решения целочисленных оптимизационных задач: метод отсечений, метод Беллмана, метод ветвей и границ. Метод ветвей и границ основан на переборе допустимых решений, но на переборе не отдельных решений, а их групп.

Частным случаем целочисленных задач являются задачи, в которых искомые переменные могут принимать не любые целые значения, а только одно из двух: либо 0, либо 1. Такие переменные называются двоичными или булевыми.

Распространенными задачами с двоичными переменными являются задачи выбора оптимального решения (варианта) из определенного числа заданных решений (вариантов). Если вариант входит в оптимальное решение, то двоичная переменная, соответствующая этому варианту, равна 1. Если вариант не входит в оптимальное решение, то соответствующая двоичная переменная равна 0. Например, если линия электропередачи входит в оптимальную электрическую сеть, то двоичная переменная, соответствующая этой линии равна 1; если линия электропередачи не входит в оптимальную электрическую сеть, то соответствующая двоичная переменная равна 0.

20) Методы дискретного программирования

В ряде практических оптимизационных задач заранее известен набор допустимых решений, из которых требуется выбрать оптимальное решение. Например, одно КУ заданной мощности можно разместить в узлах 1,2…n СЭС. Требуется выбрать оптимальный узел размещения КУ, соответствующий выбранному критерию. В ряде других задач искомые переменные могут принимать не любые, а только определенные значения, из которых требуется выбрать значения переменных, отвечающие оптимальному решению. Например, в заданном узле СЭС нужно установить КУ, мощность которого может быть равной значениям Из этого ряда требуется выбрать оптимальное значение мощности КУ, соответствующее выбранному критерию.

Эти задачи относят к задачам выбора вариантов из числа заданных и решаются методами дискретного программирования. В этих методах наряду с традиционными переменными используются двоичные переменные. Мат. модель задач дискретного программирования содержит целевую функцию, систему ограничений и граничные условия. Зависимости между переменными в целевой функции и системе ограничений могут быть как линейными, так и нелинейными. Задаваемые значения дискретных переменных могут быть любыми, в том числе и целочисленными.

21) Оптимизация при случайной исходной информации

Достаточно часто исходная информация или ее часть представляют собой случайные величины или случайные функции. В частности, мощности нагрузок в проектируемой системе электроснабжения можно считать случайными величинами, а изменения во времени напряжений в узлах существующей системы электроснабжения – случайными функциями. Для решения оптимизационных задач со случайной исходной информацией используются методы стохастического программирования.

Случайной величиной s называется такая величина, которая может принять то или иное значение, причем заранее неизвестно, какое именно.

Случайная величина s может быть непрерывной или дискретной. В заданном диапазоне изменения случайной величины количество значений дискретной случайной величины ограничено, а количество значений непрерывной случайной величины не ограничено. Примером непрерывной случайной величины является величина напряжения в некотором узле системы электроснабжения. Примером дискретной случайной величины является количество генераторов, одновременно работающих в энергосистеме.

Математическим ожиданием случайной величины называется ее среднее значение, полученное в результате n реализаций:



Среднеквадратичное (стандартное) отклонение определяет разброс значений случайной величины относительно ее математического ожидания:



Важной характеристикой случайной величины служит вероятность Р появление этой случайной величины в конкретном интервале значений.

Для количественной оценки вероятности случайной величины вводится понятие функция распределения вероятности.

22) Задачи оптимизации при неопределенной исходной информации

В реальных оптимизационных задачах часто приходится искать решение в условиях неопределенности. Основной причиной неопределенности является недостаток исходной информации. Применительно к области электроэнергетики примером неопределенной (недетерминированной) информации может служить перспективный рост мощностей в развивающейся электроэнергетической системе.

Для решения оптимизационных задач с недетерминированной информацией методы математического программирования не пригодны. Здесь используется вычислительный аппарат теории игр.

В соответствии с этой теорией оптимизационная задача представляется игрой двух игроков. Первый игрок – человек, который принимает решение. В приведенном примере человек должен принять решение по расположению в энергосистеме новых электростанций, строительству линий электропередачи и подстанций. Человек – разумный игрок. Его стратегия – максимальный выигрыш или минимальный проигрыш. Другими словами - человек минимизирует затраты.

Второй игрок – энергосистема, а точнее перспективные мощности потребителей энергии. Как будет развиваться энергосистема, каковы будут мощности потребителей в перспективе – однозначно неизвестно. Стратегия энергосистемы – случайная. Она не стремится к максимальному выигрышу. Следовательно, энергосистему нельзя считать разумным игроком.

При решении оптимизационной задачи составляется платежная матрица, которая представляет собой таблицу затрат в игре двух игроков. Строки матрицы соответствуют решениям (ходам), которые может принять первый игрок. Столбцы – ходам, которые может сделать второй игрок. Процесс составления платежной матрицы достаточно сложен и в каждом конкретном случае может быть различным.

23) Основные стратегии теории игр

1.Стратегия минимума средних затрат. В соответствии с этой стратегией для каждого хода человека определяются средние затраты по всем возможным ходам системы

m

Z_{ср i} = ( z_ij) / m. (7.1)

j=1

Выбирается решение, отвечающее минимуму из совокупности i=1, 2,…n средних затрат



При этой стратегии считается, что все ходы системы имеют одинаковую вероятность, равную 1/m.

2.Миниминная стратегия. В соответствии с этой стратегией считается, что на каждый ход человека система ответит ходом , соответствующим минимальным затратам



Выбирается решение, отвечающее минимуму из совокупности i=1,2,…n минимальных затрат



Принятие решения по этой стратегии может привести к крупным просчетам, поскольку здесь учитывается самая благоприятная ситуация.

3.Минимаксная стратегия. В соответствии с этой стратегией считается, что на каждый ход человека система ответит ходом соответствующим максимальным затратам:



Выбирается решение, отвечающее минимуму из совокупности i=1,2, … n максимальных затрат:



В этой стратегии учитывается самая неблагоприятная ситуация.

4.Стратегия Гурвица. Эта стратегия учитывает самую как благоприятную, так и самую неблагоприятную ситуации. Здесь решение выбирается по условию:



где коэффициенты k и (1-k) играют роль весовых коэффициентов, с которыми учитываются минимаксная и миниминная стратегии. При k=1 имеем минимаксную стратегию, а при k=0 имеем миниминную стратегию.

Наибольшую трудность при применении этой стратегии представляет определение величины весовых коэффициентов k и (1-k). Теория игр ответа на этот вопрос не дает. Для каждой конкретной задачи весовые коэффициенты определяются индивидуально, на основе имеющегося опыта.

Таким образом, для решения оптимизационной задачи при недетерминированной исходной информации теория игр выдвигает ряд стратегий. Поскольку формально все стратегии равноправны, окончательное решение должно выбираться на основе:

• 
  анализа решений, полученных по каждой стратегии;
  
• 
  опыта проектировщика;
  
• 
  особенностей конкретной задачи.