конспект урока сокращение алгебраических дробей. Конспект урока Сокращение алгебраических дробей. Сокращение алгебраических дробей
 Скачать 44.75 Kb. Скачать 44.75 Kb.
|
|
Тема урока: Сокращение алгебраических дробей Тип урока: изучение нового материала Задачи: Создать условия для развития умений сокращать алгебраические дроби Планируемые результаты Предметные: Научиться сокращать алгебраические дроби Метапредметные: Познавательные: ориентироваться на разнообразные способы решения задач Регулятивные: учитывать правила в планировании и контроле способа решения Коммуникативные: контролировать действия партнера Личностные: формировать интерес к изучению математики и желанию применить приобретённые знания умения и навыки Цели: систематизировать знания учащихся, ввести понятие алгебраической дроби, научить раскладывать на множители числитель и знаменатель дроби развивать творческую самостоятельность учащихся, коммуникативные навыки, формировать интерес к предмету. План урока: Организационный момент. (2 мин) Актуализация опорных знаний Мотивационный этап Формулировка темы и целей урока. Изучение нового материала Закрепление изученного материала Итог урока. Рефлексия Домашнее задание. Оснащение урока: Раздаточный материал. Мультимедийное приложение. Ход урока 1 . Организационный момент. Учитель отмечает отсутствующих, проверяет готовность к уроку. 2. Мотивационный этап Учитель: Новое понятие в математике не появляется из неоткуда. Оно появляются тогда, когда в нём ощущается объективная необходимость. Именно так появились в математике отрицательные числа, обыкновенные и десятичные дроби. Сегодня мы с вами ввёдем новое понятие. Предпосылки для этого у нас имеются. Вернёмся к § 23, где мы обсуждали «Деление одночлена на одночлен». Тогда мы рассмотрели ряд примеров. Выделим несколько из них: 1. Разделить одночлен  на на 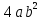 . . Решили мы его так: вместо записи 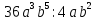 использовали черту дроби использовали черту дроби 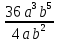 Это позволило вместо записей 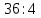 , ,  , , 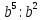 , использовать черту дроби, сделать решение примера более наглядно , использовать черту дроби, сделать решение примера более наглядно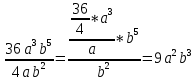 2. Разделить одночлен 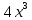 на на  . . Действуя по тому же образцу, мы получили: 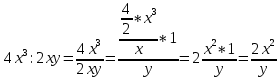 В этом случае мы заметили, что одночлен 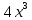 не удалось разделить на одночлен не удалось разделить на одночлен  так, чтобы получился одночлен так, чтобы получился одночленНо ведь математические модели могут содержать деление любых одночленов. Поэтому требуется ввести новое понятие, понятие алгебраической дроби.  - алгебраическая дробь. - алгебраическая дробь.3. Формулировка целей и темы урока Учитель: Сформулируйте тему урока. Учащиеся: Тема урока: «Сокращение алгебраических дробей» Учитель: А теперь нам нужно сформулировать цели и задачи. Учащиеся: Цель нашего урока будет: научиться сокращать алгебраические дроби. А задачи: 1. Повторить способы разложения на множители и формулы сокращенного умножения 2. Нам нужно сформулировать определение алгебраической дроби; 3.Нам нужно выяснить, как работать с алгебраическими дробями и сокращать их, составить алгоритм; 4 Практиковаться сокращать алгебраические дроби. Учитель: Молодцы! Так как единственный путь, ведущий к знанию – это деятельность, теперь приступим к выполнению поставленных задач 4. Актуализация опорных знаний Учитель: Какие способы разложения на множители вы знаете? Учащиеся: способ вынесения общего множителя за скобки, способ группировки, разложение на множители с помощью формул сокращенного умножения. Учитель: - Записать на доске, как разложить на множители квадрат разности двух выражений - Записать, как разложить разность кубов двух выражений (один из учащихся выполняет задания на доске) Одним из основных умений, которые нам сегодня понадобятся – разложение многочлена на множители. Проверим, готовы ли мы. Задание: Необходимо найти для многочлена, который записан в левом столбце, его разложение в правом столбце. (Выполняют задание по парам) 1. 49 + 14у + у2; А) (7 – у)(7 + у) 2. 2у2 – 20у + 50; Б) (у – 5)(у2 + 5у + 25) 3. х3 – х2у; В) 2(у – 5)2 4. 49 – у2; Г) (7 + у)2 5. у3 – 125; Д) (у – 3)3 6. у3 – 9у2 + 27у – 27; Е) х2(х – у) Учащиеся: Ответ: Г, В, Е, А, Б, Д. Учитель: Предлагаю учащимся оценить себя: “Отлично знаю формулы” - нет ошибок; “Хорошо знаю формулы” - 1 ошибка; “Удовлетворительно знаю формулы” - 2 ошибки Учащиеся: Оценивают свою работу. Учитель: Отлично! Теперь можно приступать к выполнению следующих задач. 5. Изучение нового материала Учитель: Ребята, давайте попробуем сами сформулировать, что называется алгебраической дробью. Учащиеся: Высказывают свои предположения Учитель: (После ответов учеников) Алгебраическая дробь – это деление одного многочлена P на другой многочлен Q: 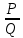 , P – числитель дроби, Q – знаменатель дроби , P – числитель дроби, Q – знаменатель дробиРассмотрим примеры алгебраических дробей:  , , 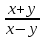 , , 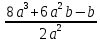 Иногда алгебраическую дробь можно заменить многочленом: 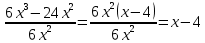 Т.е. многочлен 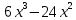 удалось разделить на удалось разделить на 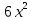 . В частном получилось . В частном получилось  Похожая ситуация уже встречалась нам: дробь 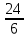 можно заменить целым числом 4, а дробь можно заменить целым числом 4, а дробь 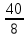 числом 5. Однако дробь числом 5. Однако дробь 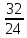 целым числом заменить не удастся, но эту дробь можно упростить. Чтобы упростить данное выражение, нужно разложить числитель и знаменатель на простые множители: целым числом заменить не удастся, но эту дробь можно упростить. Чтобы упростить данное выражение, нужно разложить числитель и знаменатель на простые множители: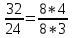 Теперь можно сократить на общий множитель 8, тогда получим  По аналогии действия с алгебраическими дробями заключаются в следующем: нужно и числитель, и знаменатель разложить на множители, а после этого, если есть возможность общие множители сократить. Рассмотрим примеры: Пример 1: 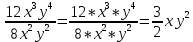 В результате деления одночленов получен новый одночлен; Пример 2: 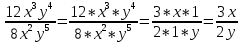 В результате деления одночленов получена алгебраическая дробь. Пример 3:  Применим в числителе формулу для квадрата суммы, а в знаменателе формулу для разности квадратов двух выражений  Пример 4: 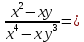 Раскладываем числитель и знаменатель на множители методом вынесения общего множителя: 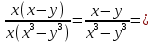 Применим в знаменателе формулу разности кубов:  Пример 5: 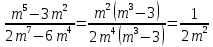 Алгоритм сокращения алгебраических дробей 1 Разложить числитель и знаменатель алгебраической дроби на множители 2 Сократить общие множители 3 Записать ответ (получившееся выражение) 6 Закрепление пройденного материала. Сократите дробь Выполните задание из учебника 35,5(б), 35.10(б, г),35.16(а, г), 35.19 (б),35.22(а), 8. Включение в систему знаний, повторение. Учащимся предлагается из листов, на которых записаны этапы алгоритма, составить полный алгоритм. Листы нужно закрепить на доске с помощью магнитов. Найди ошибку. Учитель: Каждому человеку свойственно ошибаться. Не ошибается только тот, кто ничего не делает. Проверьте равенства: 1) 2) 3) 4) 5) 9 Домашнее задание. Рефлексия настроения. Итог урока 1 Достигли ли мы поставленных целей? 2 Что мы сегодня делали на уроке? 3 Сформулируйте алгоритм сокращения алгебраических дробей - Разложить числитель и знаменатель алгебраической дроби на множители - Сократить общие множители - Записать ответ (получившееся выражение) 4 Заполните таблицу. Рефлексия
Эта таблица поможет выявить ваши слабые стороны. Проработайте их, устраните пробел. На следующий урок возьмите их собой. 8. Домашнее задание 35,23 (а,б) 35,30(б) 35,33(а)
|
