ЗАОЧНИКИ_ЭКОНОМЕТРИКА_ЛЕКЦИИ. Степанов в. Г. Краткое историческое введение

• Название: Степанов в. Г. Краткое историческое введение
• Анкор: ЗАОЧНИКИ_ЭКОНОМЕТРИКА_ЛЕКЦИИ.doc
• Дата: 25.04.2017
• Размер: 0.78 Mb.
• Имя файла: ЗАОЧНИКИ_ЭКОНОМЕТРИКА_ЛЕКЦИИ.doc
• Тип: Курс лекций; #5473
• страница: 1 из 8

КУРС ЛЕКЦИЙ – ЭКОНОМЕТРИКА ДЛЯ ЗАОЧНИКОВ.
СТЕПАНОВ В.Г.


КРАТКОЕ ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ

Эконометрика – молодая наука, которая своим происхождение обязана развитию статистики и совершенствованию ее методов с одной стороны. С другой стороны эконометрика многим обязана в своем становлении и развитии укреплению позиций системного подхода в современной науке в целом и особенно усовершенствованию математических методов и моделей в экономике. Формирование эконометрики в качестве самостоятельной науки (а не просто раздела статистики) относится к первой трети 20 века и окончательное ее утверждение в виде важного самостоятельного направления в экономических исследованиях относят к середине 20 века.

Эконометрика рассматривает модели реальных экономических систем, которые значительно ближе к реальным рыночным процессам, чем модели экономической теории и в то же время характеризуются значительно большей целостностью (общесистемным подходом) по сравнению с старыми статистическими моделями. Последние нередко представляли эклектический набор разрозненных методов, искусственно собранных вместе и не объединенных одной интегрирующей идеей. Сами эконометрические модели – это по сути своей математические модели, а именно, уравнения (уравнения регрессии), не учитывающие упорядоченности данных во времени; математические соотношения, известные как временные ряды и фактически тоже своеобразные уравнения, описывающие процессы с дискретным временем, развитие их в хронологически упорядоченной последовательности; наконец, системы уравнений (системы эконометрических уравнений), которые успешно применяются для описания макроэкономических процессов и систем.

Несколько конкретнее эконометрика - это существенно междисциплинарная наука, возникшая на стыке экономики, высших методов статистики, математической статистики и в самое последнее время информационных технологий, эффективно реализующих интеграцию этих наук. От первых простейших попыток применения точных количественных методов математики к экономическим проблемам она довольно быстро перешла к использованию методов математической статистики для решения задач экономики и успешно развивает применение математической статистики и даже теории нечетких множеств и нечеткой логики к исследованию сложных процессов социально-экономической природы.

Еще в рамках статистики – способствуя зарождению эконометрики – ученые-экономисты и статистики занимались исследованием макроэкономических проблем на основе временных рядов таких показателей, как валютные курсы и пр. Изучался рынок труда, разрабатывались методы статистической проверки теории производительности организации труда на производстве. Приблизительно в это время (19 век) метод множественной регрессии был применен для оценки функции спроса.

Следующим важным этапом стали работы по применению основных методов математической статистики (корреляционно-регрессионного анализа, анализа временных рядов, метода множественной регрессии) для изучения социально-экономических явлений и процессов, включая оценку функции спроса. Тогда же (первая половина XX века) выполнялись исследования по циклическим процессам в экономике и выделению бизнес-циклов. Так изучение динамики временных рядов и экстраполяция подмеченных закономерностей в сочетании с использованием некоторых базовых теоретических предпосылок привело к построению экономических барометров (гарвардский барометр). Концепция экономического барометра использует следующую важную идею: в динамике различных компонентов экономического процесса имеются такие показатели, изменение которых опережает изменение других компонентов. Таким образом, показатели, изменение которых опережает в своем развитии изменение других показателей, являются в некотором роде предвестниками последних. Конкретно для гарвардского барометра имеется 5 групп показателей. Они затем сводятся в три отдельные кривые: одна характеризует фондовый рынок, другая – товарный рынок, третья кривая – денежный рынок. В основу прогноза с использованием гарвардского барометра было положено свойство каждой отдельной кривой повторять движение остальных кривых в определенной последовательности и с определенным отставанием.

Однако в конце первой трети двадцатого века эффективность подобных методов стала снижаться и их применение сошло на нет. Это связано с существенным изменением структуры мировых экономических отношений и изменением природы регулирующих факторов в экономике, в частности переходом к кейнсианской модели воздействия на экономику со стороны государства. Одновременно пытались применить методы Фурье-анализа и периодограмм к эконометрическим построениям.

Необходимость использования моделирования (в эконометрике это особенно очевидно), а не простого совершенствования вычислительных методов определяется тем, что многие объекты (или проблемы, относящиеся к этим объектам) непосредственно исследовать или вовсе невозможно, или же это исследование требует много времени и средств. Процесс моделирования включает три элемента: 1) субъект (исследователь), 2) объект исследования, 3)модель, опосредствующую отношения познающего субъекта и познаваемого объекта. Модель сначала строится – первый этап; затем исследуется – второй этап; после этого полученные знания аккуратно переносятся на исследуемую реальную систему – третий этап. Только после этого переходят к практической проверке и использованию полученных выводов (знаний) в реальной жизни, например, решению задачи прогноза – четвертый этап.

На этапе построения модели используются гипотезы о виде статистической зависимости и определяются неизвестные (на этом этапе) коэффициенты (параметры) моделей при помощи метода наименьших квадратов (МНК). Далее модель исследуется с применением методов математической статистики (проверки гипотез) – второй этап. На третьем этапе выполняются наиболее сложные и тонкие процессы переноса полученных знаний о модели на реальную систему – они требуют особого внимания и аккуратности. Затем наступает наиболее ответственный четвертый этап проверки полученных выводов в реальных условиях и их соответствующего применения, которые не выполняются автоматически, а требуют особого внимания к границам применимости этих выводов.
ЛЕКЦИЯ 1. ПОСТРОЕНИЕ МОДЕЛИ: ОПРЕДЕЛЕНИЕ

ПАРАМЕТРОВ МОДЕЛИ (МНК).
Вернемся к первому этапу. После формирования гипотезы о виде зависимости (функционального вида правой части уравнения регрессии) необходимо выполнить определение входящих в уравнение коэффициентов – подбор параметров зависимости - и тем самым установить окончательно модель явления. Это осуществляется методом наименьших квадратов (МНК). Получающаяся модель проверяется на значимость с помощью различных критериев, представляющих основу статистической проверки гипотез, например, если

y_i = f(x_i) + ε_{i ,} где f(x_i)=a_o + a₁x (1.2)

то коэффициенты определяются по МНК условием обращения в минимум функции

∑(y_i-a_o-a₁x)²→min, (1.3)

где требование минимизации квадратов отклонений приводит к системе нормальных уравнений (линейные алгебраические уравнения особого вида) для нахождения из нее коэффициентов a_i.

В экономике и, следовательно, в эконометрике исследуемые явления и характеризующие их величины это сложные случайные процессы и случайные величины, параметры этих процессов. Случайные величины в процессе анализа представляются состоящими из постоянной компоненты и случайной компоненты. При этом постоянная составляющая это математическое ожидание, или среднее арифметическое (среднее) значение исходной случайной величины:

= (1.4)

Если же данные не сгруппированы, то все частоты f равны 1 и получаем формулу простого среднего:

(1.5)

Среднее случайной компоненты, или остатка равно нулю. Если бы это оказалось не так, то это ненулевое значение следовало бы включить в среднее значение исходной случайной величины и, таким образом, все свелось бы к предыдущему. Мера разброса (вариации) случайной величины, или, что то же, ее распределения, - это дисперсия.

Первоначально дисперсия определяется как среднее квадрата разности между самой случайной величиной и средним этой случайной величины:

Var(χ) = ² = (1.6)
В этом выражении коэффициенты ƒ не что иное как веса, или весовые коэффициенты значений величины χ . Это попросту величины, показывающие сколько раз входят те или иные значения в данное эмпирическое распределение величины χ для дискретных распределений или же в данный интервал (данную группу) для непрерывных распределений.

Часто при расчетах используют выражение для дисперсии в виде разности среднего от квадрата исходной случайной величины и квадрата среднего от нее:

σ² = - (1.7)

Тогда окончательно для дисперсии исходной случайной величины получаем, что она равна дисперсии остатка, поскольку вся вариация исходной случайной величины равна вариации остатка, просто по самому определению остатка.

В действительности, кроме самых простых и редких случаев, неизвестно распределение случайной величины и даже основные характеристики изучаемой генеральной совокупности. Требуется получить информацию о случайной величине, характеризующей данное явление или процесс или соответственно генеральной совокупности, из результатов наблюдений. Совокупность результатов наблюдений представляет собой выборку из генеральной совокупности и по этим данным (выборки) с применением подходящей формулы и методов оценивания (прежде всего метода наименьших квадратов) получают приближенное значение неизвестной характеристики (параметра) исследуемой случайной величины или в терминах статистики генеральной совокупности.

Эконометрика использует для изучения различных явлений и процессов признаки, характеризующие эти явления и процессы. Признаки могут быть количественными и атрибутивными, не поддающимися непосредственно количественному измерению. Эконометрика сосредоточена преимущественно на исследовании явлений и процессов, характеризующихся количественными признаками. Тем не менее, она способна исследовать и взаимосвязи между атрибутивными (не количественными) признаками. Сами количественные признаки это фактически случайные величины, которые описываются своими распределениями (совокупностью принимаемых значений и совокупностью вероятностей, с которыми эти значения принимаются). Соответственно для признаков определяются средние, а сами случайные величины могут быть представлены в виде суммы средней и остатка, характеризующего случайные флуктуации.

у = + ε, (1.8)

где средняя (первое слагаемое) может быть приближена или просто заменена некоторой функцией, например линейной:

= a_o + a₁x (1.9)
Это представление имеет глубокий смысл и будет неоднократно использоваться и обсуждаться далее. Далее помимо среднего для признака как для случайной величины определяется дисперсия, которая служит мерой вариации признака в целом (интегральная характеристика колеблемости признака).

D=σ²= (1.10)

Эконометрика исследует взаимозависимости между признаками и динамику их изменения во времени. Признаки, зависящие от других называются зависимыми, или объясняющими. Признаки от которых зависят первые (зависимые) называются независимыми, или факторами, или регрессорами. Далее мы увидим, что их так называемая независимость друг от друга отнюдь не носит абсолютный характер. Тем не менее понятие независимости факторов является весьма важным и весьма полезным начальным предположением. После исследования соответствующих базовых моделей начального уровня удается строить и изучать более сложные и более совершенные модели, в которых возможно учитывать частичную зависимость факторов.

Также естественно, что в качестве начальных базовых моделей используются простейшие зависимости, например линейные. После этого рассматривают модели, которые можно преобразовать к линейным. И наконец, только после этого существенно нелинейные модели. О том, каков точный смысл этих понятий речь пойдет в следующих лекциях.

Прежде всего, необходимо определить остаток (иначе отклонения, или погрешности) для каждого конкретного наблюдения. Этот остаток после принятия гипотезы линейной зависимости определяется как разность между фактическим значением наблюденной зависимой величины у и ее расчетным значением, получаемым по значению фактора х и формуле линейной зависимости у от х.

Линия графика (линейной зависимости), или линия регрессии должна быть такова, чтобы указанные остатки являлись минимальными. Как понимать требование минимальности именно всех остатков? Ведь уменьшая одни остатки, мы всегда с необходимостью будем увеличивать другие. Наилучший способ это потребовать минимизации суммы квадратов остатков. Остатки еще называют отклонения. В этом случае говорят о минимизации суммы квадратов отклонений. Это одно и то же. Наилучшее соответствие кривой точкам наблюдений получилось бы в предельном случае абсолютно точного соответствия, когда кривая (в нашем случае прямая) пройдет точно через все точки. Но это нереально для линии регрессии, ввиду наличия случайного члена и ошибок наблюдений.

Именно описанный только что принцип минимизации квадратов остатков и его реализация называются методом наименьших квадратов (МНК). Поскольку существует также модификация и развитие его, то говорят также о традиционном, или обычном МНК. В математике (математической статистике и теории приближенных вычислений) МНК рассматривается в качестве одного из наиболее важных и эффективных методов приближенных вычислений и методов оценивания. По существу именно ситуации, когда система алгебраических линейных уравнений не имеет точного решения, является наиболее общей и важной с практической точки зрения. И в большинстве случаев удается найти содержательные приближенные решения, дающие ответ на вопросы, поставленные в данной задаче.

Важно понимать, что в МНК переменные и коэффициенты как бы меняются местами. Из требования минимизации суммы квадратов остатков вытекает довольно простая система линейных алгебраических уравнений. Она называется нормальная система, или система нормальных уравнений. В этой системе уравнений в качестве известных величин выступают величины, получаемые в результате перемножения, возведения в квадрат и последующего суммирования наблюденных значений переменных. Надо отчетливо понимать, что, несмотря на свой нередко относительно громоздкий вид, это всего лишь известные величины, играющие теперь роль коэффициентов системы. С другой стороны сами исходные коэффициенты линейной зависимости (параметры) неизвестны. Именно их и надо определить из системы нормальных уравнений.

Для решения системы алгебраических линейных уравнений существуют различные методы от простого исключения переменных до использования определителей и обратных матриц, метод Гаусса, систематизирующий и обобщающий исключение переменных и называемый поэтому методом последовательного исключения неизвестных. Для случая двух переменных эти формулы нахождения решения системы нормальных уравнений довольно просты. Для множественной регрессии, когда рассматриваются зависимости от множества факторов такие формулы становятся более громоздкими.

Важно то, что в очень большом количестве исследуемых ситуаций выборочная дисперсия весьма близка к генеральной дисперсии и является хорошим приближением и тем самым хорошей оценкой для генеральной дисперсии, кроме отдельных специальных случаев. В то же время выборочное среднее не является достаточно хорошей оценкой, а служит всего лишь грубым первоначальным приближением к оценке генерального среднего, которое уточняется с помощью формул, использующих выборочную дисперсию.

Итак, оценки – это приближения к неизвестным величинам с некоторыми важными хорошими свойствами. Опираясь на оценки важнейших характеристик случайных величин, выявляют и исследуют связи между ними, определяют величину этих связей, исходя из важнейших показателей, характеризующих статистические зависимости между величинами и процессами. Мерой взаимосвязи между переменными является выборочная ковариация, которая для последовательности наблюдений двух переменных представляет среднее произведений разностей результатов наблюдений и их соответствующих средних. Есть другая форма вычисления ковариации, когда она представляется в виде среднего попарных произведений соответствующих результатов наблюдений этих двух переменных, из которого вычитается произведение средних этих двух переменных:

Cov(x,y)=å(x-`x)(y-`y)/n=[(∑xy)/n] – [] (1.11)

Ковариация легко вычисляется, но при всей ее простоте она вовсе не является наилучшим измерителем взаимосвязи между величинами. Более точно характеризует зависимость коэффициент корреляции. Выборочный коэффициент корреляции, или просто выборочная корреляция это просто частное от деления выборочной ковариации на произведение выборочных дисперсий соответствующих переменных. Преимущество коэффициента корреляции перед ковариацией заключается в том, что ковариация зависит от единиц, в которых измеряются переменные, коэффициент корреляции это величина безразмерная.

r=Cov(x,y)/Övar(x)var(y) (1.12)

Построение модели парной регрессии
Рассмотрим простой пример элементарного задания по эконометрике. В соответствии с вариантом задания, используя статистический материал необходимо.

1. Рассчитать параметры уравнения линейной парной регрессии.

2. Оценить тесноту связи с помощью показателей корреляции и детерминации.

3. Используя коэффициент эластичности, определить степень связи факторного признака с результативным.

4. Определить среднюю ошибку аппроксимации.

5. Оценить с помощью F – критерия Фишера статистическую надежность моделирования.

Исходные данные для построения модели парной регрессии приведены в таблице 1.

Линейное уравнение парной регрессии имеет вид

, (1.13)

где - оценка условного математического ожидания y; b₀, b₁ –эмпирические коэффициенты регрессии, подлежащие определению.

Таблица 1.1. Исходные данные

№ п/п	Область	Средний размер назначенных ежемесячных пенсий, у.д.е., у	Прожиточный минимум в среднем на одного пенсионера в месяц, у.д.е., х
1	Орловская	232	166
2	Рязанская	215	199
3	Смоленская	220	180
4	Тверская	222	181
5	Тульская	231	186
6	Ярославская	229	250

Эмпирические коэффициенты регрессии b₀, b₁ будем определять с помощью инструмента «Регрессия» надстройки «Анализ данных» табличного процессора MS Excel.

Алгоритм определения коэффициентов состоит в следующем .

1. Вводим исходные данные в табличный процессор MS Excel.

2. Вызываем надстройку Анализ данных (рисунок 1.1).

3. Выбираем инструмент анализа Регрессия (рисунок 1.2).

4. Заполняем соответствующие позиции окна Регрессия( рисунок 1.3).

5. Нажимаем кнопку ОК окна Регрессия и получаем протокол решения задачи (рисунок1.4)
Р
исунок 1.1. Активизация надстройки Анализ данных

Р
исунок 1.2. Выбор инструмента Регрессия

Рисунок 1.3. Окно Регрессия





Рисунок 1.4. Протокол решения задачи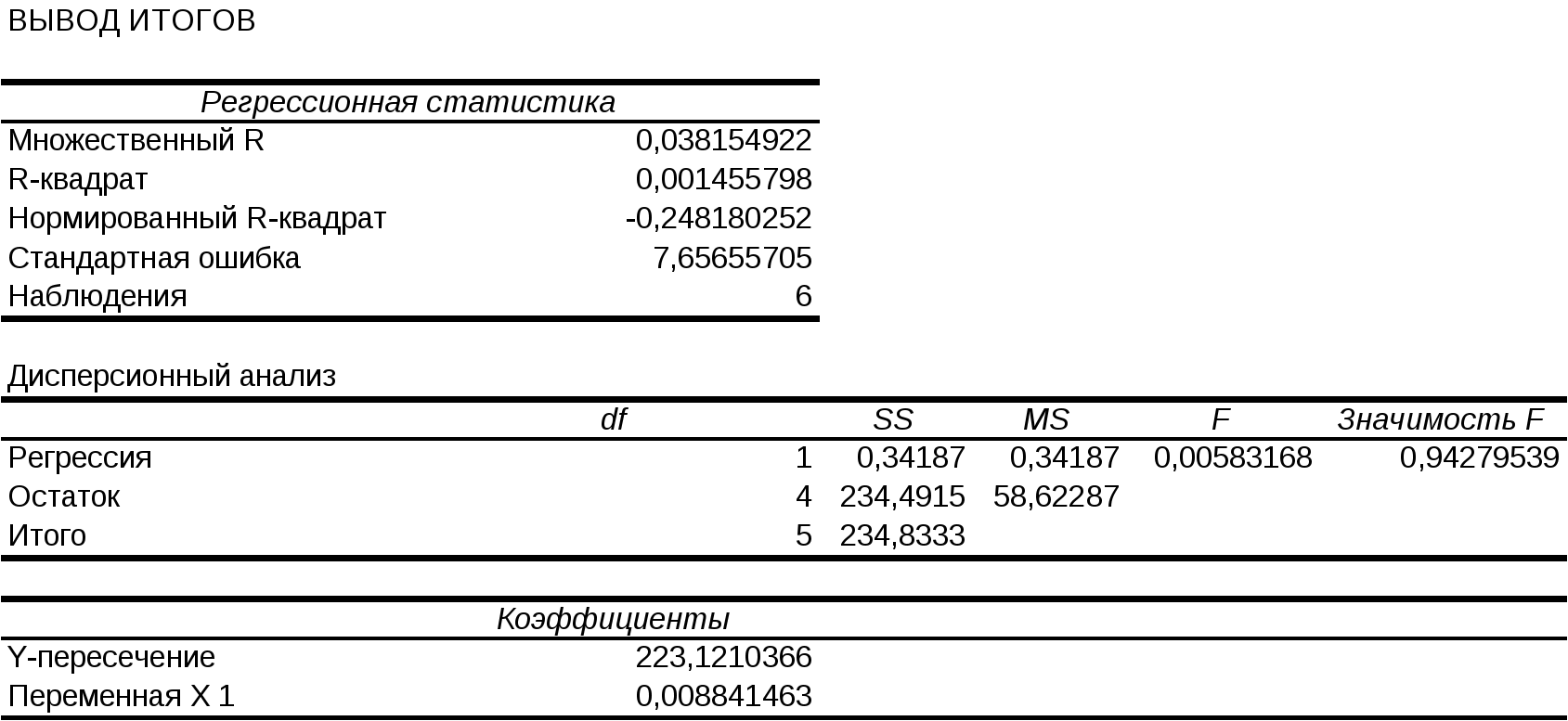




Из рисунка 1.4 видно, что эмпирические коэффициенты регрессии соответственно равны b₀ = 223, b₁ = 0, 0088. См. две последние строки под заголовком коэффициенты