Теория сигналов и систем. РГР 86 вариант. Задача 1 3 Задача 2 12 Задача 3 22 Задача 4 26 Заключение 29 Список использованных источников 31
 Скачать 242.95 Kb. Скачать 242.95 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Комсомольский-на-Амуре государственный университет» Факультет энергетики и управления Кафедра «ПЭ» РАСЧЁТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ по дисциплине «Теория сигналов и систем» 86 вариант Студент группы 0БМБ-1 Е.С. Ильченко Преподаватель С.Г. Марущенко 2022 Содержание Задача 1 3 Задача 2 12 Задача 3 22 Задача 4 26 Заключение 29 Список использованных источников 31 Задача 1 Построить амплитудную спектральную диаграмму четной периодической последовательности прямоугольных импульсов (рис. 1, а) с длительностью tи и амплитудой U при двух значениях периода T1 и T2. Проанализировать изменение спектра последовательности в зависимости от скважности импульсов. Как изменится спектр рассматриваемой последовательности при совмещении начала отсчета времени с фронтом одного из импульсов (рис. 1, б) 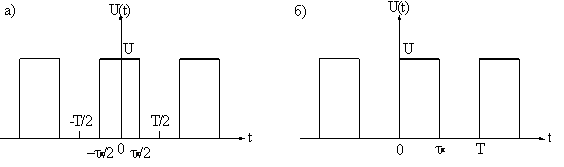 Рисунок 1.1 - Периодическая последовательность прямоугольных импульсов: а – четная; б – сдвинутая на tи/2 Исходные данные: 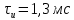 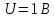 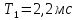 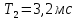 Решение: Четная периодическая последовательность прямоугольных импульсов. Данная в задании последовательность импульсов является периодической, для построения амплитудной спектральной диаграммы применим спектральное разложения в ряд Фурье. Для периодического сигнала ряд Фурье принимает вид: 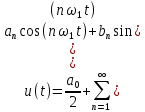 где 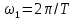 - основная частота последовательности - основная частота последовательностиТак как сигнал u(t) четный относительно начала координат (t=0), то коэффициент при синусоидальных составляющих будут равны нулю ( 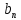 =0). =0).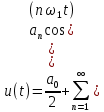 Найдем коэффициенты 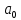 и и 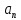 ряда Фурье: ряда Фурье: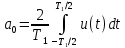 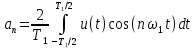 Отношение 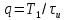 называется скважность последовательности. называется скважность последовательности. Математическая модель сигнала при  будет иметь вид s(t)=U. Тогда выражения коэффициентов ряда примут вид: будет иметь вид s(t)=U. Тогда выражения коэффициентов ряда примут вид: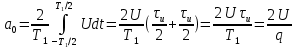 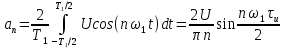 Подставив выражения для коэффициентов ряда в формулу для периодического сигнала ряд Фурье, получем окончательную формулу ряда Фурье для последовательности: 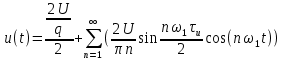 Заменим 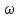 на выражение на выражение 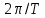 в знаменателе выражения стоящего под знаком синуса, сократим первое слагаемое: в знаменателе выражения стоящего под знаком синуса, сократим первое слагаемое: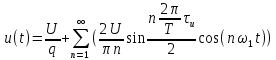 Заменим отношение  на отношение на отношение 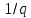 , разделим и умножим множитель перед синусом на q и упростим выражение: , разделим и умножим множитель перед синусом на q и упростим выражение: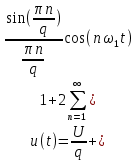 Графическое изображение коэффициентов ряда Фурье называется спектральной диаграммой. Так как коэффициенты при синусоидальных составляющих равны нулю, то амплитудный спектр нашей последовательности будет представлен коэффициентами при косинусоидальных составляющих, взятых по абсолютному значению:  Для построения спектральных диаграмм подставим численные значения и произведем вычисления для получения точек графиков. Для периода 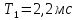  Таблица 1.1 - значения амплитуд гармоник сигнала 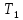
Продолжение таблицы 1.1
 Рисунок 1.2 - Амплитудная спектральная диаграмма для 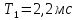 Для периода 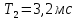 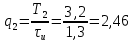 Таблица 1.2 - значения амплитуд гармоник сигнала 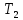
Продолжение таблицы 1.2
 Рисунок 1.3 - Амплитудная спектральная диаграмма для  Вывод: ширина спектра увеличивается при увеличении скважности импульса, также увеличивается количество составляющих и их амплитуды медленне затухают, ширина основного лепестка спектра увеличивается. Оценим ширину основного лепестка амплитудных спектров: Для периода 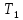 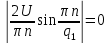 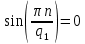 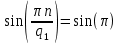 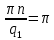 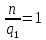  Для периода 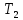  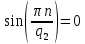 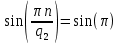 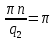 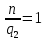 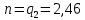 В случае если начало отсчета совпадает с началом отсчета, то сигнал перестает быть четным и коэффициенты ряда Фурье не будут равны нулю при синусоидальных составляющих. Находим коэффициенты: 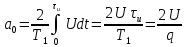 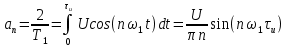  Выражение для ряда Фурье данной последовательности: 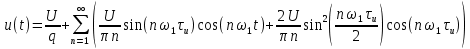 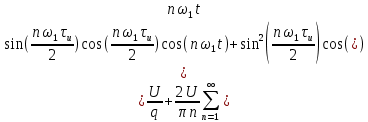 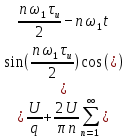  Амплитудный спектр последовательности:  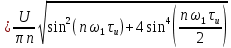   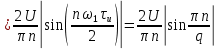 Данная нечетная последовательность прямоугольных импульсов имеет также фазовый спектр, который будет определяться следующим выражением: 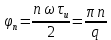  Найдем амплитудный спектр последовательности:     Вывод: амплитудный спектр сигнала не зависит от совмещения начала отсчета с фронтом одного из импульсов или с серединой импульса. Мы видим, что при совмещении начала отсчета с фронтом одного из импульсов амплитудный спектр сигнала не изменится. Данная нечетная последовательность прямоугольных импульсов также имеет фазовый спектр. 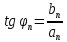 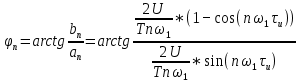 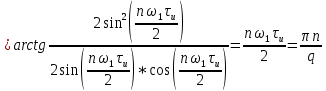  Фаза гармонических составляющих изменяется по линейному закону и возрастает с ростом порядкового номера n гармоники. Подставим в формулы численные данные и произведем расчеты. Таблица 1.3 - Фазовый спектр сигнала с периода Т1
Таблица 1.4 - Фазовый спектр сигнала с периода Т2
|
