математика. Документ Microsoft Word (10) (1). min, при этом x
 Скачать 190.19 Kb. Скачать 190.19 Kb.
|
|
1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях. Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 0, которая указывает на максимальную чистую стратегию A1. Верхняя цена игры b = min(bj) = 4. Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 0 ≤ y ≤ 4. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии). 2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы. Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью. Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если aij ≥ akj для всех j Э N и хотя бы для одного j aij > akj. В этом случае говорят также, что i-я стратегия (или строка) – доминирующая, k-я – доминируемая. Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если для всех j Э M aij ≤ ail и хотя бы для одного i aij < ail. В этом случае j-ю стратегию (столбец) называют доминирующей, l-ю – доминируемой. С позиции проигрышей игрока В стратегия B2 доминирует над стратегией B1 (все элементы столбца 2 меньше элементов столбца 1), следовательно, исключаем 1-й столбец матрицы. Вероятность q1 = 0. С позиции проигрышей игрока В стратегия B2 доминирует над стратегией B5 (все элементы столбца 2 меньше элементов столбца 5), следовательно, исключаем 5-й столбец матрицы. Вероятность q5 = 0. С позиции проигрышей игрока В стратегия B3 доминирует над стратегией B4 (все элементы столбца 3 меньше элементов столбца 4), следовательно, исключаем 4-й столбец матрицы. Вероятность q4 = 0.
В платежной матрице отсутствуют доминирующие строки. Мы свели игру 2 x 6 к игре 2 x 3. Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш. Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I. В матрице присутствуют отрицательные элементы. Для упрощения расчетов добавим к элементам матрицы (1). Такая замена не изменит решения игры, изменится только ее цена (по теореме фон Неймана).
3. Находим решение игры в смешанных стратегиях. Решим задачу геометрическим методом, который включает в себя следующие этапы: 1. В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A1, правый - стратегии A2 (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S1 = (p1,p2). 2. На левой оси ординат откладываются выигрыши стратегии A1. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A2. Решение игры (2 x n) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет. Выделяем нижнюю границу выигрыша B2NB3. Максиминной оптимальной стратегии игрока A соответствует точка N, лежащая на пересечении прямых B2B2 и B3B3, для которых можно записать следующую систему уравнений: y = 1 + (7 - 1)p2 y = 10 + (0 - 10)p2 Откуда p1 = 7/16 p2 = 9/16 Цена игры, y = 35/8 Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений, исключив стратегию B1, которая дает явно больший проигрыш игроку B, и, следовательно, q1 = 0. q2+10q3 = y 7q2 = y q2+q3 = 1 или q2+10q3 = 35/8 7q2 = 35/8 q2+q3 = 1 Решая эту систему, находим: q2 = 5/8. q3 = 3/8. 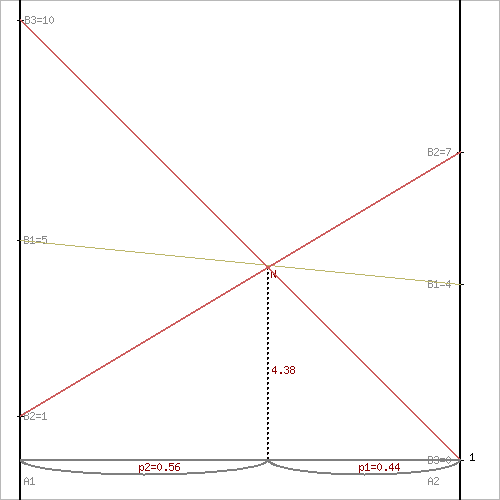 Поскольку ранее к элементам матрицы было прибавлено число (1), то вычтем это число из цены игры. Цена игры: y = 35/8 - 1 = 27/8 Ответ: Цена игры: y = 27/8, векторы стратегии игроков: Q(0, 5/8, 3/8), P(7/16, 9/16) 4. Проверим правильность решения игры с помощью критерия оптимальности стратегии. ∑aijqj ≤ v ∑aijpi ≥ v M(P1;Q) = (4*0) + (0*5/8) + (9*3/8) = 3.375 = v M(P2;Q) = (3*0) + (6*5/8) + (-1*3/8) = 3.375 = v M(P;Q1) = (4*7/16) + (3*9/16) = 3.438 ≥ v M(P;Q2) = (0*7/16) + (6*9/16) = 3.375 = v M(P;Q3) = (9*7/16) + (-1*9/16) = 3.375 = v Все неравенства выполняются как равенства или строгие неравенства, следовательно, решение игры найдено верно. Поскольку из исходной матрицы были удалены и столбцы, то найденные векторы вероятности можно записать в виде: P(7/16,9/16) Q(0,0,5/8,0,0,3/8) Задание № 4, Транспортная задача. Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 13 + 25 + 34 = 72 ∑b = 19 + 41 + 12 + 33 = 105 Как видно, суммарная потребность груза в пунктах назначения превышает запасы груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) базу с запасом груза, равным 33 (72—105). Тарифы перевозки единицы груза из базы ко всем потребителям полагаем равны нулю. Занесем исходные данные в распределительную таблицу.
|
