математика. Документ Microsoft Word (10) (1). min, при этом x
 Скачать 190.19 Kb. Скачать 190.19 Kb.
|
|
Этап I. Поиск первого опорного плана. 1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj. Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены. Искомый элемент равен c14=3. Для этого элемента запасы равны 13, потребности 33. Поскольку минимальным является 13, то вычитаем его. x14 = min(13,33) = 13.
Искомый элемент равен c31=5. Для этого элемента запасы равны 34, потребности 19. Поскольку минимальным является 19, то вычитаем его. x31 = min(34,19) = 19.
Искомый элемент равен c23=6. Для этого элемента запасы равны 25, потребности 12. Поскольку минимальным является 12, то вычитаем его. x23 = min(25,12) = 12.
Искомый элемент равен c24=6. Для этого элемента запасы равны 13, потребности 20. Поскольку минимальным является 13, то вычитаем его. x24 = min(13,20) = 13.
Искомый элемент равен c34=7. Для этого элемента запасы равны 15, потребности 7. Поскольку минимальным является 7, то вычитаем его. x34 = min(15,7) = 7.
Искомый элемент равен c32=8. Для этого элемента запасы равны 8, потребности 41. Поскольку минимальным является 8, то вычитаем его. x32 = min(8,41) = 8.
Искомый элемент равен c42=0. Для этого элемента запасы равны 33, потребности 33. Поскольку минимальным является 33, то вычитаем его. x42 = min(33,33) = 33.
В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность потребителей удовлетворена, а план соответствует системе ограничений транспортной задачи. 2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным. Значение целевой функции для этого опорного плана равно: F(x) = 3*13 + 6*12 + 6*13 + 5*19 + 8*8 + 7*7 + 0*33 = 397 Этап II. Улучшение опорного плана. Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0. u1 + v4 = 3; 0 + v4 = 3; v4 = 3 u2 + v4 = 6; 3 + u2 = 6; u2 = 3 u2 + v3 = 6; 3 + v3 = 6; v3 = 3 u3 + v4 = 7; 3 + u3 = 7; u3 = 4 u3 + v1 = 5; 4 + v1 = 5; v1 = 1 u3 + v2 = 8; 4 + v2 = 8; v2 = 4 u4 + v2 = 0; 4 + u4 = 0; u4 = -4
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vj ≤ cij. Минимальные затраты составят: F(x) = 3*13 + 6*12 + 6*13 + 5*19 + 8*8 + 7*7 + 0*33 = 397 Анализ оптимального плана. Из 1-го склада необходимо весь груз направить к 4-у потребителю. Из 2-го склада необходимо груз направить к 3-у потребителю (12 ед.), к 4-у потребителю (13 ед.) Из 3-го склада необходимо груз направить к 1-у потребителю (19 ед.), к 2-у потребителю (8 ед.), к 4-у потребителю (7 ед.) Потребность 2-го потребителя остается неудовлетворенной на 33 ед. Оптимальный план является вырожденным, так как базисная переменная x42=0. 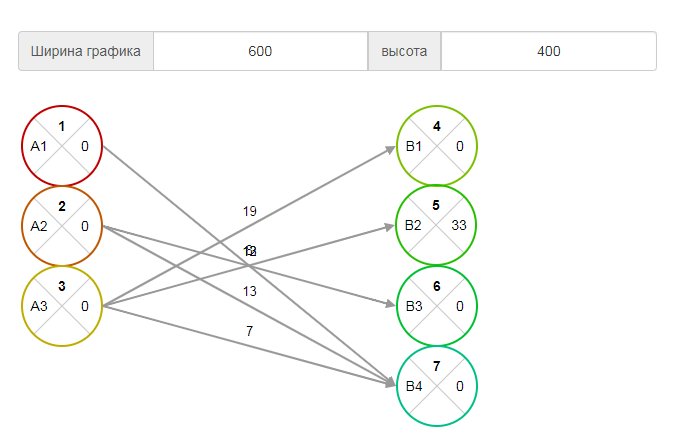 Задание № 2. Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим минимальное значение целевой функции F(X) = 108x1+112x2+126x3 при следующих условиях-ограничений. 0.1x2+0.1x3≤120 0.4x1+0.4x2+0.3x3≤600 0.8x1+0.5x2+0.6x3≤800 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≤) вводим базисную переменную x6. 0.1x2+0.1x3+x4 = 120 0.4x1+0.4x2+0.3x3+x5 = 600 0.8x1+0.5x2+0.6x3+x6 = 800 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Решим систему уравнений относительно базисных переменных: x4, x5, x6 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,120,600,800) Базисное решение называется допустимым, если оно неотрицательно.
Переходим к основному алгоритму симплекс-метода. 1. Проверка критерия оптимальности. Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 0, x2 = 0, x3 = 0 F(X) = 108*0 + 112*0 + 126*0 = 0 Примечание: 1. По какому методу пересчитываются симплекс-таблицы? Используется правило прямоугольника (метод жордановских преобразований). 2. Обязательно ли каждый раз выбирать максимальное значение из индексной строки? Можно не выбирать, но это может привести к зацикливанию алгоритма. 3. В индексной строке в n-ом столбце нулевое значение. Что это означает? Нулевые значения должны соответствовать переменным, вошедшим в базис. Если в индексной строке симплексной таблицы оптимального плана находится нуль, принадлежащий свободной переменной, не вошедшей в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. Свободную переменную, соответствующую указанному столбцу, можно внести в базис, выполнив соответствующие этапы алгоритма. В результате будет получен второй оптимальный план с другим набором базисных переменных. |
