математика. Документ Microsoft Word (10) (1). min, при этом x
 Скачать 190.19 Kb. Скачать 190.19 Kb.
|
|
Критерий оптимальности полученного решения. Если существуют такие допустимые решения X и Y прямой и двойственной задач, для которых выполняется равенство целевых функций F(x) = Z(y), то эти решения X и Y являются оптимальными решениями прямой и двойственной задач соответственно. Определение дефицитных и недефицитных (избыточных) ресурсов. Вторая теорема двойственности. Подставим оптимальный план прямой задачи в систему ограниченной математической модели: 2*0 + 3*32/5 + 1*0 + 2*2/5 = 11 > 2 1*0 + 2*32/5 + 1*0 + 3*2/5 = 8 = 8 1*0 + 1*32/5 + 1*0 + 4*2/5 = 5 = 5 1-ое ограничение выполняется как строгое неравенство, т.е. ресурс 1-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y1 = 0. Неиспользованный экономический резерв ресурса 1 составляет 9 (2-11). Этот резерв не может быть использован в оптимальном плане, но указывает на возможность изменений в объекте моделирования (например, резерв ресурса можно продать или сдать в аренду). 2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y2 ≠ 0). 3-ое ограничение прямой задачи выполняется как равенство. Это означает, что 3-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y3 ≠ 0). Двойственные оценки отражают сравнительную дефицитность различных видов ресурсов в отношении принятого в задаче показателя эффективности. Оценки показывают, какие ресурсы являются более дефицитными, (они будут иметь самые высокие оценки), какие менее дефицитными и какие совсем недефицитны (избыточны) - они будут равны нулю. Применяя теорему двойственности, получим решение двойственной задачи по известному решению исходной задачи. Найдем решение двойственной задачи у* воспользовавшись второй теоремой двойственности и известным оптимальным планом х*. Поскольку x2>0, 2-е ограничение в двойственной задаче будет равенством. Поскольку x4>0, 4-е ограничение в двойственной задаче будет равенством. Таким образом, решение двойственной задачи сводится к решению уравнений при следующих условиях: y1 = 0 3y1+2y2+y3 = 1 2y1+3y2+4y3 = 2 2y1+8y2+5y3 → max или 2y2+y3 = 1 3y2+4y3 = 2 2y1+8y2+5y3 → max Обоснование эффективности оптимального плана. При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим: 2*0 + 1*2/5 + 1*1/5 = 3/5 < 3 3*0 + 2*2/5 + 1*1/5 = 1 = 1 1*0 + 1*2/5 + 1*1/5 = 3/5 < 2 1-ое ограничение выполняется как строгое неравенство, т.е. продукцию 1-го вида производить экономически не выгодно. И действительно в оптимальном плане прямой задачи x1 = 0. При этом разница между ценами (3/5 - 3 = -22/5) показывает величину изменения целевой функции F(x) при введении дополнительной единицы xi. 2-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 2-й продукт экономически выгодно производить (убытки от производства этого вида продукции отсутствуют), а его использование предусмотрено оптимальным планом прямой задачи (x2>0). 3-ое ограничение выполняется как строгое неравенство, т.е. продукцию 3-го вида производить экономически не выгодно. И действительно в оптимальном плане прямой задачи x3 = 0. При этом разница между ценами (3/5 - 2 = -12/5) показывает величину изменения целевой функции F(x) при введении дополнительной единицы xi. Анализ устойчивости оптимального плана. Проведем анализ устойчивости оптимального плана и оценим степень влияния изменения ресурсов на значение целевой функции. Чувствительность решения к изменению коэффициентов целевой функции. Так как любые изменения коэффициентов целевой функции оказывают влияние на оптимальность полученного ранее решения, то наша цель - найти такие диапазоны изменения коэффициентов в целевой функции (рассматривая каждый из коэффициентов отдельно), при которых оптимальные значения переменных остаются неизменными. Пусть каждое значение параметра целевой функции изменится на ∆ сi. Найдем интервалы, при которых будет экономически выгодно использование ресурсов. Допустимые диапазоны изменения коэффициентов в целевой функции определятся из соотношений: Вариант расчета №1.
Отсюда получаем условие устойчивости: 1/5Δc2+1/5Δc4+-12/5≥0 1/5Δc2+1/5Δc4+-7/5≥0 -4/5Δc2+1/5Δc4+-2/5≥0 3/5Δc2-2/5Δc4+-1/5≥0 Затем последовательно находим интервалы устойчивости: Δc2≠0, Δc2=0, Δc1≤12, Δc1≤7 Δc4≠0, Δc1=0, Δc2≤12, Δc2≤7 Вариант расчета №2. Верхняя граница для: ∆c1+ ∆c1+ = |max[yk/dk1]| для dk1<0. Таким образом, 1-й коэффициент может быть увеличен на 12/5. ∆c1- = +∞ Интервал изменения равен: (c1 - ∆c1-; +∞) [3-∞;3+-12/5] = [-∞;3/5] 2-й параметр целевой функции может изменяться в пределах: ∆c2- = min [yk/d2k] для d2k>0. ∆c2+ = |max[yk/d2k]| для d2k<0. 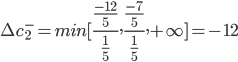 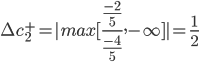 Таким образом, 2-й параметр может быть уменьшен на 12 или увеличен на 1/2. Интервал изменения равен: (c2 - ∆c-2; c2 + ∆c2+) [1+12; 1+1/2] = [13;3/2] Если значение c2 будет лежать в данном интервале, то оптимальный план не изменится. Верхняя граница для: ∆c3+ ∆c3+ = |max[yk/dk3]| для dk3<0. Таким образом, 3-й коэффициент может быть увеличен на 2/5. ∆c3- = +∞ Интервал изменения равен: (c3 - ∆c3-; +∞) [2-∞;2+-2/5] = [-∞;8/5] Чувствительность решения к изменению запасов сырья. Из теоремы об оценках известно, что колебание величины bi приводит к увеличению или уменьшению f(X). Оно определяется величиной yi в случае, когда при изменении величин bi значения переменных уi в оптимальном плане соответствующей двойственной задачи остаются неизменными. Поэтому необходимо найти такие интервалы изменения каждого из свободных членов системы ограничений исходной ЗЛП, в которых оптимальный план двойственной задачи не менялся бы. Найдем интервалы устойчивости ресурсов. Вариант расчета №1. При этом условие устойчивости двойственных оценок задачи исходит из выражения: X1=X0+ΔX=A-1(B+ΔB) в которой компоненты вектора X1 должны быть неотрицательны, т.е. все xj≥0. На этом основании для нашей задачи можно записать:
Отсюда получаем условие устойчивости: Δb1-2Δb2+Δb3+9≥0 -1/5Δb2+2/5Δb3+2/5≥0 4/5Δb2-3/5Δb3+17/5≥0 Затем последовательно находим интервалы устойчивости: Δb1≠0, Δb2=Δb3=0, Δb1≥-9 Δb2≠0, Δb1=Δb3=0, Δb2≤9/2, Δb2≤2, Δb2≥-17/4 Δb3≠0, Δb1=Δb2=0, Δb3≥-9, Δb3≥-1, Δb3≤17/3 Для корректного решения задачи необходимо ввести еще дополнительные ограничения, вытекающие из экономического содержания решаемой задачи. Предельные значения (нижняя и верхняя границы) изменения каждого из ресурсов, для которых двойственные оценки остаются неизменными, определяются еще и таким образом. Вариант расчета №2. Нижняя граница для: ∆b1- ∆b1- = min[xk/dk1] для dk1>0. Таким образом, 1-й запас может быть уменьшен на 9. 1-й вид ресурса в оптимальном плане недоиспользован, является недефицитным. Увеличение данного ресурса приведет лишь к росту его остатка. При этом структурных изменений в оптимальном плане не будет, так как двойственная оценка y1 = 0. Другими словами, верхняя граница b1+ = +∞ ∆b1+ = +∞ Интервал изменения равен: (b1 - ∆b1-; +∞) [2-9; +∞] = [-7;+∞] 2-й запас может изменяться в пределах: ∆b2- = min[xk/dk2] для dk2>0. ∆b2+ = |max[xk/dk2]| для dk2<0. 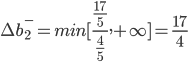 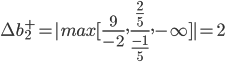 Таким образом, 2-й запас может быть уменьшен на 17/4 или увеличен на 2. Интервал изменения равен: (b2 - ∆b2-; b2 + ∆b2)+ [8-17/4; 8+2] = [15/4;10] 3-й запас может изменяться в пределах: ∆b3- = min[xk/dk3] для dk3>0. ∆b3+ = |max[xk/dk3]| для dk3<0. 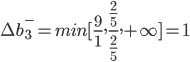 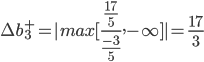 Таким образом, 3-й запас может быть уменьшен на 1 или увеличен на 17/3. Интервал изменения равен: (b3 - ∆b3-; b3 + ∆b3)+ [5-1; 5+17/3] = [4;32/3] В оптимальный план не вошла основная переменная x1, т.е. ее не выгодно использовать. Определим максимально возможное значение в рамках полученных двойственных оценок: x1 может изменяться в пределах: -9 ≤ x1 ≤ 2 Задание № 5. Число каналов 2 Длина очереди ∞ Интенсивность потока событий 2,85 Среднее время обслуживания 0,5 Исчисляем показатели обслуживания для одноканальной СМО: Интенсивность потока обслуживания: |
