основы технической механики. 1.1 Основы технической механики. 1. 1 Основы технической механики
 Скачать 1.67 Mb.
|
Кручение. Построение эпюр крутящих моментовРассмотрим кручение на примере бруса круглого сечения. Брус, испытывающий кручение, называют валом. Кручение имеет место при нагружении вала парами сил (вращающими моментами М), расположенными в плоскостях перпендикулярных к оси вала (рис.2.10).  Рис.2.10. Нагрузки, вызывающие деформацию кручения При кручении в поперечных сечениях вала возникает только один внутренний силовой фактор - крутящий момент Т. Крутящие моменты в различных поперечных сечениях вала определяют методом сечений: вал рассекают воображаемой плоскостью, перпендикулярной к продольной оси вала, (рис. 2.11, а) мысленно отбрасывают одну часть вала, а действие отброшенной части на оставшуюся заменяют крутящим моментом Т(рис. 2.11, б). 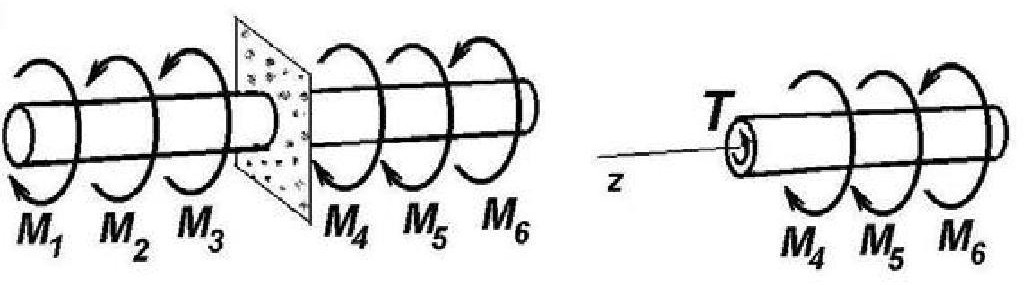 а б Рис. 2.11. К определению крутящих моментов Рассматривая равновесие оставшейся части, определяют значение Т. Крутящий момент Т в сечении вала равен алгебраической сумме внешних моментов, действующих по одну сторону от рассматриваемого сечения, относительно оси вала. Правило знаков крутящих моментов: крутящий момент в сечении считать положительным, если, глядя на проведенное сечение со стороны отброшенной части видно, что внешний момент действует против хода часовой стрелки. Так, для вала на рис. 2.10, б от момента М6 возникает положительный крутящий момент, а от моментов М4 и М5 – отрицательный. Зависимость изменения крутящих моментов по длине вала изображают в виде, т.е. эпюры крутящих моментов Т , которую строят применяя методсечений. Напряжения при кручении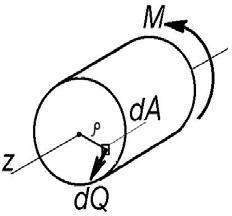 При кручении вала в его поперечном сечении на бесконечно малых площадках dA действуют элементарные внутренние поперечные силы dQ(рис.2.12). распределенные по плоскости поперечного сечения и равные, согласно выражению (2.28) dQ= τ dA.Рис. 2.12. К определению напряжений при кручении Момент одной такой элементарной силы dQотносительно оси вала dQ ρ =τ dAρ. где τ — полное касательное напряжение в точке сечения; ρ — плечо элементарной поперечной силы dQ. Тогда крутящий момент в поперечном сечении:
При деформации вала под действием внешнего момента каждое его поперечное сечение поворачивается в своей плоскости вокруг продольной оси вала на некоторый угол ϕ. Этот угол для разных сечений будет различным. В результате, прямоугольная сетка, нанесенная на поверхность вала (рис.2.13, а) превратится в сетку параллелограммов (рис.2.13, б), что свидетельствует о сдвиговом характере деформации и наличии касательных напряжений τ в поперечных сечениях вала. 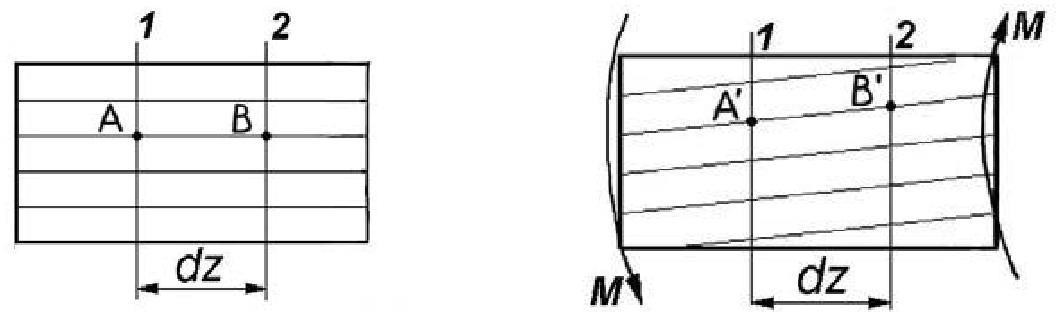 а б Рис.2.13. Характер деформации вала при кручении а –до приложения нагрузки; б– во время приложения нагрузки. Выделим из вала, как показано на рис.20, б двумя секущими плоскостями 1 и 2 элементарный цилиндр длиной dz и рассмотрим механизм его деформации. Будем считать условно, что выделенный фрагмент вала защемлен в левом сечении (рис.2.14, а). Под действием момента М правое сечение повернется относительно левого на угол dϕ. При этом бесконечно малая площадка К в правом сечении сдвинется на расстояние КК1. Волокно СК повернется, а прямой угол вблизи точки С исказится на угол γ. 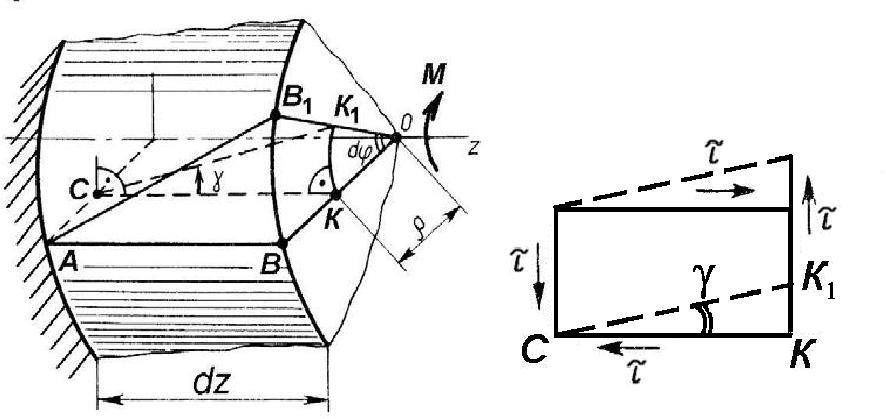 а б Рис.2.14. Механизм деформации вала при кручении а – поворот поперечного сечения; б– сдвиг в прямоугольном элементе вала. Если рассмотреть прямоугольный элемент вблизи точек С и К, то по его деформации видно (рис. 2.14, б) находится в условиях чистого сдвига, так как по его граням действуют только касательные напряжения τ, а угол γ представляет собой угол сдвига. Из рис.2.14, аследует, что КК′=γ · dz =ρ· dφ, откуда
Используя закон Гука при сдвиге, получаем зависимость, отражающую закон распределения касательных напряжений при кручении:
Учитывая формулу (2.29), получим выражение крутящего момента в сечении вала
- полярный момент инерции сечения. Мерой деформации при кручении является относительный уголзакручивания, = где dφ -абсолютныйуголзакручивания(угол поворота сечения относительно другого); dz- расстояние между сечениями. Относительный угол закручивания может быть выражен крутящий момент = = Тогда формула примет вид = (2.33) одного этими через (2.34) (2.35) Из формулы (2.35) видно, что касательные напряжения зависят от расстояния вдоль радиусов поперечного сечения вала по линейному закону. Это отражено на рис.2.15. 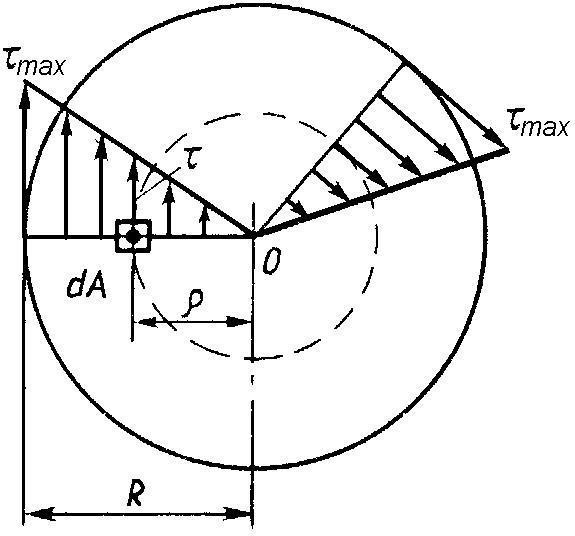 Рис.2.15. Эпюры касательных напряжений по сечению вала при кручении Видно, что касательные напряжения τ равны нулю в центре сечения и достигают значения τmax на его контуре (при ρ = ρmax = R). Поэтому рациональной формой поперечного сечения вала является кольцо. Для определения максимального касательного напряжения можно использовать выражение
  где Wρ — полярный момент сопротивления круглого сечения:Wρ = Iρ /ρmax = Iρ /R= 2Iρ / d . Для круглого сечения Wρ= π d3/16 ≈ 0,2 d3, где d – диаметр сечения. Для сечения в виде кольца Wρ= 0,2 D3(1- с4), где D– наружный диаметр кольца; с – отношение внутреннего диаметра кольца к наружному. |