основы технической механики. 1.1 Основы технической механики. 1. 1 Основы технической механики
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
Условия прочности и жесткости при растяжении и сжатииКонечной целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость. Условие прочности стержня при его растяжении (сжатии) с учетом формул (2.6, 2.7) и (2.13):
проверочный или проектный расчеты стержней, а также определять допустимую нагрузку на конструкцию. При проектном расчёте сначала определяют требуемую площадь «опасного» (самого нагруженного) поперечного сечения элемента конструкции при заданных нагрузке и материале конструкции, а затем вычисляют размеры поперечного сечения. При проверочном расчёте находят наибольшее напряжение в опасном сечении, которое сравнивают с допускаемым напряжением. В некоторых случаях необходимо определять допустимую нагрузку при известных поперечных размерах элемента и характеристиках материала. При расчётах на жёсткость работоспособность стержня оценивают
гарантированы нормальные условия работы; l-в зависимости от нагрузок, жесткости сечения и длины стержня рассчитывают по формуле (2.20). МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ Диаграммы растяженияОсновные прочностные и деформационные характеристики конструкционных материалов, необходимые для расчетов деталей на прочность и жесткость конструкций, определяют экспериментально путем проведения испытаний образцов на растяжение, сжатие, срез, кручение и изгиб. Наиболее распространенным является испытание на растяжение статической нагрузкой, позволяющее определить большинство механических характеристик материала. Для испытаний используют стандартные по форме и размерам образцы (рис.2.6). 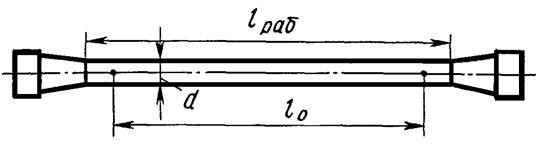 Рис. 2.6. Образец для испытаний материалов на растяжение Растяжение образцов из испытуемого материала проводят на испытательных машинах, автоматически записывающих диаграмму зависимости растягивающей силы и удлинения образца F = f( l). Чтобы исключить влияние размеров образца, диаграмму растяжения образца рассматривают в координатных осях (σ; ε). При этом на горизонтальной оси откладывается относительное удлинение образца ε = l/ l0, а на вертикальной - условное напряжение в образце σ =F/A0. Напряжение называют «условным», так как силу (нагрузку) делят на первоначальную площадь поперечного сечения образца, а не на действительную его площадь. Типичная «условная диаграмма» растяжения образца из малоуглеродистой стали, показана на рисунке 7 сплошной линией АВСDEN. 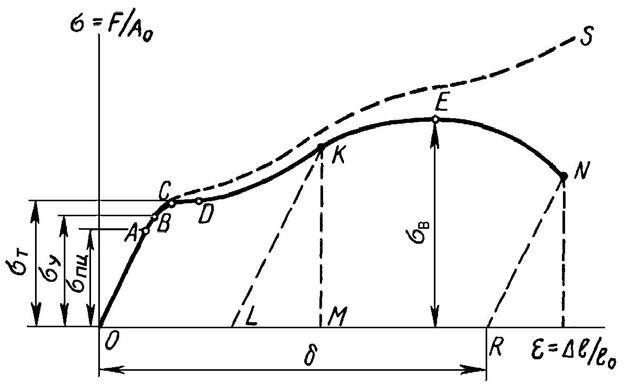 Рис.2.7. Диаграмма растяжения пластичных материалов Область диаграммы можно условно разделить на четыре участка. На участке ОА наблюдается линейная зависимость между нагрузкой и удлинением образца (зона упругости материала). Здесь свойства материала подчиняются закону Гука. На участке CD удлинение образца растет без заметного увеличения на- грузки (зона текучести), а сам горизонтальный участок диаграммы растяжения называется площадкойтекучести.Участок DE - зона упрочнения, где зависимость между нагрузкой и удлинением нелинейная. Участок EN - зона локальной пластической деформации стали, когда на образце образуется местное сужение (шейка). Образец в этой зоне удлиняется за счет локальной пластической деформаций материала в шейке. В точке N происходит разрушение образца, а пластическая деформация к этому моменту соответствует точке R на оси удлинений ε (линия NR параллельна упругому участку ОА диаграммы). Анализ диаграммы растяжения позволяет определить механические характеристики материала. Пределпропорциональностиσпц- наибольшее напряжение на диаграмме, до которого справедлив закон Гука (4). Оно соответствует для материала точке А; Пределупругостиσу- наибольшее напряжение, до достижения которого материал не получает заметных остаточных деформаций, соответствует точке В; Модульпродольнойупругости(модульЮнга)Е– коэффициент пропорциональности в уравнении закона Гука (4). Е имеет размерность напряжения (МПа) и по величине соответствует тангенсу угла наклона β упругого участка ОА диаграммы к оси удлинений ε; Пределтекучестиσт- напряжение, при котором происходит рост пластических деформаций материала без заметного увеличения нагрузки, соответствует участку СD на диаграмме. Пределомпрочностиили временнымсопротивлениемσв(рис.2.7) называют отношение максимальной силы к первоначальной площади его поперечного сечения. Следует заметить, что величина σв не является истинным напряжением, при котором образец разрушается в точке N. Если рассматривать отношение максимальной растягивающей силы не к первоначальной его площади, а к истинной площади сечения Аист, то при образовании шейки, в наиболее узком ее сечении, истинное напряжение σист.=F/Аист. перед разрывом образца на самом деле растет. Кривая OS на рис. 2.7 является «истинной диаграммой» растяжения, где напряжение σист.=F/Аист. Таким образом, истинное напряжение разрыва в точке Sсущественно больше σв, а предел прочности пластичных материалов - величина «условная». Пластические свойства материала характеризуют две величины: |
