Реферат. задание. 1. 1 Расчет параметров уравнений по отклонениям 7 2 Характеристика тесноты связи 10
 Скачать 172.65 Kb. Скачать 172.65 Kb.
|
1.1 Расчет параметров уравнений по отклонениямОсуществляется отбор факторных признаков x1,x2,...xp, оказывающих влияние на y. Исходные данные представлены временными рядами x1t,x2y,...xpt; yt. Определяются тенденции изменения временных рядов, т.е. тренды ytc=f(t); xitc=fi(t); i=1,2,…,n. Рассчитываются отклонения выравненных значений переменных от исходных величин γt=yt-f(t); εit=xit – fi(t). Выявляется наличие мультиколлинеарности, для чего вычисляются коэффициенты парной корреляции. Устанавливаются периоды запаздывания (временные лаги) во взаимодействии признаков. После корректировки состава независимых переменных приступают к оцениванию параметров уравнения множественной линейной регрессии yt=α1ε1t+ α2ε2t +... + αpεpt.(*). При наличии временного лага Lпо переменной хiв уравнение вместо еitвводится еit-L . Коэффициенты бiрекомендуется определять по методу наименьших квадратов, используя так называемые стандартизованные вiкоэффициенты. Необходимость использования коэффициентов в стандартизованном виде объясняется тем, что в уравнении (*) каждое отклонение является абсолютной величиной, такой же, как и исходные временные ряды зависимой и независимой переменных. Числовые значения отклонений представлены в соответствующих единицах измерения. Данное обстоятельство не позволяет оценивать сравнительную силу воздействия каждого аргумента на зависимую переменную путем сопоставления коэффициентов регрессии α1, α2,…, αp. Переход к стандартизованным коэффициентам заключается в замене отклонений γt, εit новыми переменными, исходя из соотношений Tγ=γt/σγt; Ti=εit/σεit , откуда γt=Tγσγt ; εit=Tiσεit. Подставив последние выражения в уравнение (*) и поделив левую и правую части на σγt, получим: Tγ=(α1T1σε1t /σγt)+(α2T2σε2t /σγt)+…+(αpTpσεpt /σγt). Переменные Т в последнем уравнении являются теперь относительными безразмерными величинами. Замена αiσεit /σγt на βi приводит уравнение к стандартизованному виду Tγ=β1T1+ β2T2+…+ βpTp , в котором βi- стандартизованные коэффициенты регрессии. Они показывают, на сколько среднеквадратических отклонений изменится зависимая переменная, если величина i-го независимого фактора увеличится или уменьшится на одно свое среднеквадратическое отклонение при условии постоянства всех остальных факторов-аргументов. Так как βi-коэффициенты являются относительными величинами, то с их помощью можно сделать вывод о степени влияния каждого фактора на функцию. Численные значения коэффициентов определяются на основе значений коэффициентов парной корреляции. Система нормальных уравнений, используемых при расчетах, имеет вид: r 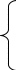 γtε1t=β1rε1tε1t+β2rε1tε2t+…+βprε1tεpt γtε1t=β1rε1tε1t+β2rε1tε2t+…+βprε1tεptrγtε2t=β1rε2tε1t+β2rε2tε2t+…+βprε2tεpt , ………………………………………… rγtεpt=β1rεptε1t+β2rεptε2t+…+βprεptεpt rγtεit=∑γεit/(∑γ2t∑ε2it)½; rεitεjt=∑εitεjt/(∑ε2it∑ε2jt)½; rεitεjt=1. Система уравнений, линейных относительно βi, может быть решена любым способом. Естественно, оценка параметров и проверка надежности найденных уравнений регрессии осуществляются при использовании Microsoft Excel и множества статистических пакетов обработки данных, таких как SPSS, Statistica, Minitab и других. В данном случае важен содержательный алгоритм расчетов. Например, при использовании формул Крамера вi=∆i/∆, где ∆i – определитель, получаемый из главного определителя ∆ путем замены i-го столбца столбцом из свободных членов. После решения системы и определения βi-коэффициентов находятся коэффициенты αi=βiσγt/σεit , осуществляется переход от относительных величин к абсолютным и уравнению yt=∑pj=1ajxjt+εt, t=1,2,…n. Для оценки параметров уравнения временные ряды должны быть не менее 15-20 лет, а прогнозный период в 2-3 раза короче. Прогнозные значения xjt можно оценить на основе экстраполяции, методом экспоненциального сглаживания, на основе трендов или уравнений авторегрессии, методом экспертных оценок. При необходимости в модели должны найти отражение периоды запаздывания. |
