Предел
|
1
|
Областью определения функции  является интервал… является интервал…
|
1. (-∞; +∞)
2. (-∞; -1)  (-1; 1) (-1; 1) (1;+∞) (1;+∞)
3. (-∞; 1) (3; +∞) (3; +∞)
4. (-∞; 1] [1; +∞) [1; +∞)
|
2
|
Областью определения функции  является интервал… является интервал…
|
1. (-∞; +∞)
2. (-∞; -3) (-3; 3) (-3; 3) (3; +∞) (3; +∞)
3. (-∞; -3) (-3; +∞) (-3; +∞)
4. (-∞; 3] [3; +∞) [3; +∞)
|
3
|
Областью определения функции  является интервал… является интервал…
|
1. (-∞; +∞)
2. (-∞; -3)  (-3; 3) (-3; 3) (3;+∞) (3;+∞)
3. (-∞; -3) (-3; +∞) (-3; +∞)
4. (-∞; 3] [3; +∞) [3; +∞)
|
4
|
Первый замечательный предел раскрывает неопределенность вида…
|
1. ∞-∞
2. 
3. 1∞
4. 
|
5
|
Второй замечательный предел раскрывает неопределенность вида…
|
1. ∞-∞
2. 
3. 1∞
4. 
|
6
|
Вычислить  … …
|
1. 0
2. 1
3. 
4. 2
|
7
|
Вычислить  … …
|
1. 0
2. 1
3. 
4. 2
|
8
|
Вычислить  … …
|
1. 0
2. 1
3. 
4. 2
|
9
|
Вычислить  … …
|
1. 0
2. 1
3. 
4. 2
|
10
|
Вычислить  … …
|
1. 0
2. 1
3. 
4. 2
|
11
|
Вычислить  … …
|
1. 0
2. 1
3. 
4. 2
|
12
|
Вычислить  … …
|
1. 0
2. 1
3. 
4. 2
|
13
|
Вычислить  … …
|
1. 0
2. 1
3. 
4. 2
|
14
|
При делении постоянной величины на бесконечно большую получается…
|
1. неопределенность
2. бесконечно малая величина
3. ограниченная величина
4. бесконечно большая величина
|
15
|
Предел  равен… равен…
|
1. 0
2. -9
3. -1/9
4. 1
|
16
|
Значение предела  равно… равно…
|
1. 1
2. -1
3. 0
4. 
|
17
|
Предел  равен… равен…
|
1. ∞
2. 5/2
3. 0
4. 5
|
18
|
Предел вида  численно равен величине биологической популяции… численно равен величине биологической популяции…
|
1. 1600
2. 1200
3. 800
4. 400
|
19
|
Начальная величина биологической популяции  равна … равна …
|
1. 2900
2. 3000
3100
100
|
20
|
Значение предела  равно… равно…
|
1. 1
2. 6
3. 
4. 16
|
21
|
Значение предела  равно… равно…
|
1. 1
2. 0
3. 
4. 2
|
Производная функции
|
1
|
Производная функции  равна… равна…
|
1. 
2. 
3. 
4. 
|
2
|
Производная функции  равна… равна…
|
1. 4х
2. 2х
3. 
4. х
|
3
|
Производная функции  равна… равна…
|
1. 4х
2. 2х
3. 
4. х
|
4
|
Производная функции  равна… равна…
|
1. 4х
2. 2х
3. 
4. х
|
5
|
Производная функции  равна… равна…
|
1. 1
2. 2х
3. 0
4. х
|
6
|
Производная функции  равна… равна…
|
1. 1
2. 2х
3. 0
4. х
|
7
|
Закон движения материальной точки имеет вид  , где , где  - координата точки в момент времени - координата точки в момент времени  . Тогда скорость точки при . Тогда скорость точки при  равна… равна…
|
1. 10
2. 14
3. 24
4. 20
|
8
|
Предел приращения функции  к приращению аргумента к приращению аргумента  при при  - это: - это:
|
1. неопределенный интеграл
2. определенный интеграл
3. производная функции
4. бесконечно малая величина
|
9
|
Динамика развития биологической популяции определяется уравнением вида…
|
1. 
2. 
3. 
4. 
|
10
|
Сколько раз необходимо продифференцировать функцию, чтобы найти интервалы возрастания и убывания ее графика
|
1. 0
2. 1
3. 2
4. 3
|
11
|
Производная второго порядка функции  равна… равна…
|
1. 
2. 
3. 
4. 
|
12
|
Производная второго порядка функции  равна… равна…
|
1. 
2. 
3. 
4. 
|
13
|
При исследовании функции
у = f (x) и построении ее графика производная  позволяет найти: позволяет найти:
|
1. уравнения асимптот
2. экстремум
3. координаты точек перегиба
4. координаты точек пересечения с осью ОХ
|
14
|
Вычислить производную функции 
|
1. 
2. 
3. 
4. 
|
15
|
Вычислить производную функции 
|
1. 
2. 
3. 
4. 
|
16
|
Производная функции  в точке (0,0) равна… в точке (0,0) равна…
|
1. 0
2. 2х
3. 1
4. х
|
17
|
Производная функции  в точке (0,0) равна… в точке (0,0) равна…
|
1. 0
2. 2х
3. 1
4. х
|
18
|
Первая производная функции  это: это:
|
1. скорость
2. ускорение
3. площадь
4. объем
|
19
|
Вторая производная функции  это: это:
|
1. скорость
2. ускорение
3. площадь
4. объем
|
Функция нескольких переменных
|
1
|
Частная производная по  функции функции  равна… равна…
|
1. 
2. 
3. 
4. 
|
2
|
Частная производная  функции функции  равна… равна…
|
1. 
2. 
3. 
4. 
|
3
|
Частная производная по  функции функции  равна… равна…
|
1. 
2. 
3. 0
4. 1
|
4
|
Частная производная по уфункции  равна… равна…
|
1. 
2. 
3. 0
4. 1
|
5
|
Частная производная по  функции функции  равна… равна…
|
1. 
2. 
3. 0
4. 1
|
6
|
Частная производная поу функции  равна… равна…
|
1. 
2. 
3. 0
4. 1
|
7
|
Чтобы исследовать функцию двух переменных на экстремум необходимо найти…
|
1. частные производные первого порядка
2. частные производные второго порядка
3. частные производные первого и второго порядков
4. частные производные первого, второго порядков и смешанные частные производные второго порядка
|
8
|
Графиком функции двух переменных является …
|
1. поверхность
2. прямая
3. окружность
4. эллипс
|
Интегральное исчисление
|
1
|
Первообразная функции  равна… равна…
|
1. 
2. 
3. 
4. 
|
2
|
Функция  может иметь первообразных … может иметь первообразных …
|
1. одну
2. ни одной
3. две
4. бесконечное множество
|
3
|
Формула интегрирование по частям имеет вид…
|
1. 
2. 
3. 
4. 
|
4
|
Значение интеграла  равно… равно…
|
1. 0
2. 1
3. 2
4. 3
|
5
|
Формула Ньютона – Лейбница имеет вид…
|
1. 
2. 
3. 
4. 
|
6
|
Значение определенного интеграла  равно… равно…
|
1. 
2. 
3. 
4. 3
|
7
|
Значение определенного интеграла  равно… равно…
|
1. 
2. 
3. 
4. 3
|
8
|
Значение определенного интеграла  равно… равно…
|
1. 1
2. 
3. 
4. 3
|
9
|
Геометрический смысл определенного интеграла – это…
|
1. угол наклона касательной к графику функции в точке касания
2. площадь криволинейной трапеции
3. объем тела вращения
4. скорость движения точки
|
10
|
Чтобы найти численность биологической популяции за период времени от  до до  , скорость размножения которой , скорость размножения которой  , нужно вычислить… , нужно вычислить…
|
1. 
2. 
3. 
4. 
|
11
|
Интеграл  является… является…
|
1. определенным
2. несобственным
3. неопределенным
4. табличным
|
12
|
Интеграл  равен… равен…
|
1. 
2. 
3. 
4. 
|
13
|
Интеграл  равен… равен…
|
1. 
2. 
3. 
4. 
|
14
|
Определенный интеграл выражает процесс…
|
1. суммирования
2. умножения
3. составления баланса
4. определения процентов
|
15
|
Интеграл  называется… называется…
|
1. определенным
2. неопределенным
3. несобственным
4. табличным
|
16
|
Интеграл  называется… называется…
|
1. определенным
2. неопределенным
3. несобственным
4. табличным
|
17
|
Интеграл  называется… называется…
|
1. определенным
2. неопределенным
3. несобственным
4. табличным
|
18
|
Интеграл 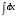 равен… равен…
|
1. 1
2. 10
3. - 1
4. - 10
|
Теория вероятности
|
1
|
Количество перестановок в слов «зачет» равно…
|
1. 24
2. 120
3. 5
4. 20
|
2
|
Формула Р(А) = m/n определяет
|
1. вероятность события
2. количество перестановок
3. количество сочетаний
4. количество размещений
|
3
|
Формула 
определяет
|
1. вероятность события
2. количество перестановок
3. количество сочетаний
4. количество размещений
|
4
|
Формула 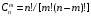
определяет
|
1. вероятность события
2. количество перестановок
3. количество сочетаний
4. количество размещений
|
5
|
Формула  определяет определяет
|
1. вероятность события
2. количество перестановок
3. количество сочетаний
4. количество размещений
|
6
|
Единицы измерения вероятности ..
|
1. единицы
2. проценты
3. сантиметры
4. градусы
|
7
|
Вероятность события меняется на множестве…
|
1. (-∞; ∞)
2. [0; 1)
3. [0; 1]
4. (0; 1)
|
8
|
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее пяти очков, равна…
|
1. 
2. 
3. 
4. 
|
9
|
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,6 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
|
1. 0,18
2. 0,15
3. 0,9
4. 0,2
|
10
|
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,6 и 0,3 соответственно. Тогда вероятность того, что в цель не попадут оба стрелка, равна…
|
1. 0,18
2. 0,15
3. 0,9
4. 0,28
|
11
|
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,15. Тогда вероятность банкротства обоих предприятий равна…
|
1. 0,765
2. 0,15
3. 0,015
4. 0,25
|
12
|
Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид…
|
1. (8,4; 10)
2. (8,6; 9,6)
3. (8,5; 11,5)
4. (10; 10,9)
|
13
|
Непрерывная случайная величина Х задана плотностью распределения вероятностей 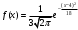 . Тогда математическое ожидание этой нормально распределенной случайной величины равно… . Тогда математическое ожидание этой нормально распределенной случайной величины равно…
|
1. 4
2. 3
3. 18
4. 9
|
14
|
При подбрасывании монеты событие А, состоящее в том, что она не упадет на землю является…
|
1. почти возможным
2. невозможным
3. достоверным
4. совместным
|
15
|
Брошена игральная кость. Вероятностью события А- (выпало четное число очков) является…
|
1. 
2. 1
3. 
4. 
|
16
|
Суммой вероятностей противоположных событий является…
|
1. 
2. 1
3. -1
4. 0
|
17
|
Сумма вероятностей двух событий А-взошло семя, В-не взошло семя равна:
|
1. 
2. 1
3. 
4. 
|
18
|
Уравнение  является формулой … является формулой …
|
1. Пуассона
2. локальной Лапласа
3. интегральной Лапласа
4. Бернулли
|
19
|
Формула Бернулли применяется, если общее число испытаний не более …
|
|
20
|
Математическое ожидание, дисперсия, среднее квадратичное отклонение – это характеристики
|
1. дифференциальные
2. интегральные
3. числовые
4. функциональные
|
21
|
Для какого события А его вероятность Р(А) = 1?
|
1. достоверного
2. противоположного
3. невозможного
4. зависимого
|
22
|
Известна вероятность события Р(А) = 2/3. Тогда вероятность противоположного события равна…
|
1. -2/3
2. 1/3
3. 0
4. 1
|
23
|
В результате вычисления вероятности случайного события может быть получено значение…
|
1. 1,5
2. 1
3. -0,3
4. 100
|
24
|
По условиям задачи: n = 5000,
m = 3, p = 0,001 можно определить, что событие является…
|
1. случайным
2. равновозможным
3. противоположным
4. редким
|
25
|
Числовой характеристикой случайной величины является…
|
1.наивероятнейшее число
2. гипотеза
3.математическое ожидание
4.условная вероятность
|
26
|
Дискретная случайная величина задана верно, если для закона ее распределения сумма вероятностей…
|
1. положительна
2. равна 10
3. меньше единицы
4. равна единице
|
27
|
Дан закон распределения вероятностей дискретной случайной величины  : :
Тогда значение  равно… равно…
|
1. -0,7
2. 0,7
3. 0,1
4. 0,2
|
28
|
Дискретная случайная величина  задана верно, если для ее закона распределения задана верно, если для ее закона распределения
 принимает значение… принимает значение…
|
1. 0,3
2. 0,1
3. -1
4. 0
|
29
|
Для какого события А его вероятность Р(А) = 0?
|
1. достоверного
2. противоположного
3. невозможного
4. зависимого
|
30
|
По оценкам экспертов вероятности для двух птенцов выжить при температуре окружающей среды 25 градусов, равны по 0,9. Тогда вероятность, что оба птенца птенца выживут равна…
|
1. 0,9
2. 1
3. 0,81
4. 0,01
|
31
|
По оценкам экспертов вероятности для двух птенцов выжить при температуре окружающей среды 25 градусов, равны по 0,9. Тогда вероятность, что оба птенца птенца погибнут равна…
|
1. 0,9
2. 1
3. 0,81
4. 0,01
|
 Скачать 1.02 Mb.
Скачать 1.02 Mb.