Линейная алгебра
|
|
Задание
|
Вариант ответа
|
1
|
Матрица 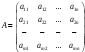
представляет собой…
|
1. число
2. переменную величину
3. прямоугольную таблицу
4. функцию
|
2
|
Размер матрицы
А = 
равен…
|
1. 3х2
2. 6
3. 2х3
4. 5
|
3
|
Размер матрицы 
равен…
|
1. 3х1
2. 1х1
3. 1х3
4. 3
|
4
|
Размер матрицы
 равен… равен…
|
1. 4х4
2. 12
3. 4х3
4. 3х4
|
5
|
Размер матрицы
 равен… равен…
|
1. 2х2
2. 10
3. 2х5
4. 5х2
|
6
|
Размер матрицы
 равен… равен…
|
1. 3х2
2. 3
3. 2х4
4. 2х3
|
7
|
Размер матрицы
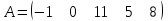 равен... равен...
|
1. 1х5
2. 5х1
3. 1
4. 5
|
8
|
Дана матрица  . .
Тогда сумма элементов, расположенных на главной диагонали этой матрицы равна…
|
1. 9
2. -7
3. 5
4. 10
|
9
|
Дана матрица 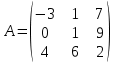 . .
Тогда сумма элементов, расположенных на главной диагонали этой матрицы равна…
|
|
10
|
Дана матрица 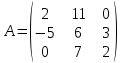 . .
Тогда сумма элементов, расположенных на главной диагонали этой матрицы равна…
|
|
11
|
Дана матрица  . .
Тогда сумма элементов, расположенных на побочной диагонали этой матрицы равна…
|
1. 9
2. -6
3. 4
4. -7
|
12
|
Дана матрица 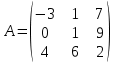 . .
Тогда сумма элементов, расположенных на побочной диагонали этой матрицы равна…
|
|
13
|
Дана матрица 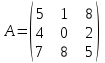 . .
Тогда сумма элементов, расположенных на побочной диагонали этой матрицы равна…
|
|
14
|
Дана матрица  . .
Тогда произведение элементов, расположенных на главной диагонали, равно…
|
|
15
|
Дана матрица 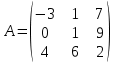 . .
Тогда произведение элементов, расположенных на главной диагонали этой матрицы равно…
|
|
16
|
Дана матрица 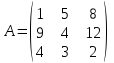 . .
Тогда произведение элементов, расположенных на главной диагонали этой матрицы равно…
|
|
17
|
Дана матрица  . .
Тогда произведение элементов, расположенных на побочной диагонали, равно…
|
|
18
|
Дана матрица 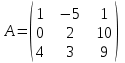 . .
Тогда произведение элементов, расположенных на побочной диагонали этой матрицы равно…
|
|
19
|
Дана матрица 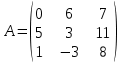 . .
Тогда произведение элементов, расположенных на побочной диагонали этой матрицы равно…
|
|
20
|
Какое действие можно выполнить над матрицами
А =  и В = и В = 
|
1. сложение
2. вычитание
3. деление
4. умножение
|
21
|
Если  , то матрица 5А имеет вид… , то матрица 5А имеет вид…
|
1. 
2. 
3. 
4. 
|
22
|
Если  , то матрица 2А имеет вид… , то матрица 2А имеет вид…
|
1. 
2. 
3. 
4. 
|
23
|
Если  , то матрица 2А имеет вид… , то матрица 2А имеет вид…
|
1. 
2. 
3. 
4. 
|
24
|
Если  , то матрица , то матрица  имеет вид… имеет вид…
|
1. 
2. 
3. 
4. 
|
25
|
Если  , то матрица , то матрица  имеет вид… имеет вид…
|
1. 
2. 
3. 
4. 
|
26
|
Над матрицами А и В можно выполнить операцию
сложения, если у них…
|
равное количество строк
равное количество столбцов
3. одинаковая размерность
4. разная размерность
|
27
|
Для матриц
 и и 
сумма А + В равна…
|
1. 
2. 
3. 
4. 
|
28
|
Для матриц
 и и 
сумма А + В равна…
|
1. 
2. 
3. 
4. 
|
29
|
Для матриц
 и и 
разность А – В равна…
|
1. 
2. 
3. 
4. 
|
30
|
Для матриц
 и и 
разность А -В равна…
|
1. 
2. 
3. 
4. 
|
31
|
Для матриц
 и и 
сумма А + В равна…
|
1. 
2. 
3. 
4. 
|
32
|
Матрицу А можно умножить на матрицу В, если …
|
1. число строк матрицы А равно числу строк матрицы В
2. число строк матрицы А равно числу столбцов матрицы В
3. матрицы А и В любые
4. число столбцов матрицы А равно числу строк матрицы В
|
33
|
Произведение матриц

представляет собой матрицу…
|
1. 
2. (10)
3. (-3)
4. (7)
|
34
|
Если  , ,  , тогда матрица , тогда матрица  имеет вид … имеет вид …
|
1. 
2. 
3. 
4. 
|
35
|
Произведение матриц

представляет собой матрицу…
|
1. 
2. ( 10)
3. (-13)
4. (-5)
|
36
|
Произведение матриц

представляет собой матрицу…
|
1. 
2. (10)
3. (17)
4. (-5)
|
37
|
Над матрицами нельзя выполнить действие…
|
1. умножение на число
2. деление
3. умножение
4. возведение в степень
|
38
|
Если матрицы А и В имеют одинаковую размерность, то над ними можно выполнить действие… (более одного ответа)
|
1. деление
2. возведение в степень
3. сложение
4. вычитание
|
39
|
Матрица, у которой от нуля отличны только элементы главной диагонали, называется…
|
1. треугольной
2. диагональной
3. симметрической
4. матрицей-строкой
|
40
|
Даны матрицы: А2x4, В5x2, С5x1. Какое произведение существует …
|
1. 
2. 
3. 
4. 
|
41
|
Даны матрицы: А2x4, В3x5, С5x1. Какое произведение существует …
|
1. 
2. 
3. 
4. 
|
42
|
Над матрицей  можно выполнить действие…(более одного ответа) можно выполнить действие…(более одного ответа)
|
1. транспонирования
2. возведения в степень
3. деления на другую
матрицу
4. извлечения корня любой степени
|
43
|
Схема контактов первого рода в эпидемиологии может быть задана при помощи…
|
1. матрицы
2. суммы матриц
3. разности матриц
4. произведения матриц
|
44
|
Схема контактов второго рода в эпидемиологии может быть задана при помощи…
|
1.матрицы
2.суммы матриц
3.разности матриц
4.произведения матриц
|
45
|
Какая из матриц может представлять контакты первого порядка в эпидемиологии
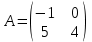
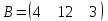
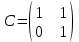
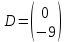
|
|
46
|
Какая из матриц может представлять контакты первого порядка в эпидемиологии
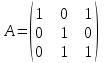
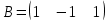
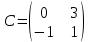
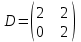
|
|
47
|
Какие из матриц могут представлять контакты первого порядка в эпидемиологии (более одного ответа)
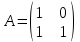
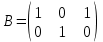
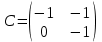
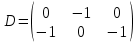
|
|
48
|
Какие из матриц могут представлять контакты первого порядка в эпидемиологии (более одного ответа)
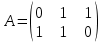
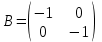
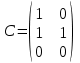
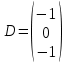
|
|
49
|
Какая из матриц может представлять контакты второго порядка в эпидемиологии
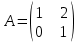
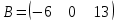
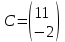
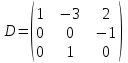
|
|
50
|
Какая из матриц может представлять контакты второго порядка в эпидемиологии
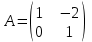
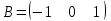
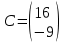
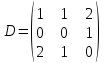
|
|
51
|
Какие из матриц могут представлять контакты второго порядка в эпидемиологии (более одного ответа)
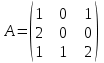
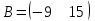
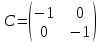
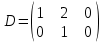
|
|
52
|
Какие из матриц могут представлять контакты второго порядка в эпидемиологии (более одного ответа)
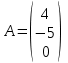
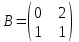
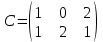
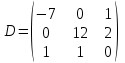
|
|
53
|
Система уравнений называется линейной, если
|
1. все уравнения линейны.
2. линейны четные уравнения.
3. линейны нечетные уравнения.
4. линейно хотя бы одно уравнение.
|
54
|
Решением системы линейных уравнений называют…
|
1. любой набор переменных
2. набор значений переменных, обращающий уравнения системы в верные тождества
3. набор значений переменных, обращающий уравнения системы в нули
4. набор значений переменных, обращающий уравнения системы в неверные тождества
|
55
|
Система линейных алгебраических уравнений называется однородной, если….
|
1. свободные слагаемые правой части больше нуля
2. свободные слагаемые правой части равны нулю
3. свободные слагаемые правой части равны единице
4. хотя бы одно свободное слагаемое правой части равно нулю
|
56
|
Система линейных алгебраических уравнений называется неоднородной, если….
|
1. хотя бы одно свободное слагаемое правой части не равно нулю
2. свободные слагаемые правой части равны нулю
3. свободные слагаемые правой части равны единице
4. хотя бы одно свободное слагаемое правой части равно нулю
|
57
|
Для решения системы трех линейных алгебраических уравнений с тремя переменными методом Гаусса применяют….
|
1. сумму матриц
2. разность матриц
3. расширенную матрицу
4. произведение матриц
|
58
|
Система линейных алгебраических уравнений называется совместной, если ….
|
1. она не имеет решений
2. она имеет хотя бы одно решение
3. количество уравнений меньше количества переменных
4. количество уравнений больше количества переменных
|
59
|
Система линейных алгебраических уравнений называется несовместной, если ….
|
1. она не имеет решений
2. она имеет хотя бы одно решение
3. количество уравнений меньше количества переменных
4. количество уравнений больше количества переменных
|
60
|
Матрица
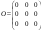 является является
|
1. единичной
2. нулевой
3. диагональной
4. пустой
|
 Скачать 1.02 Mb.
Скачать 1.02 Mb.
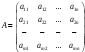
 равен…
равен…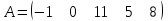 равен...
равен... .
. 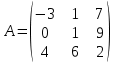 .
. 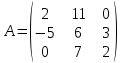 .
.  .
. 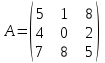 .
.  .
. 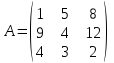 .
.  .
. 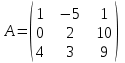 .
. 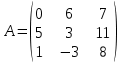 .
.  , то матрица
, то матрица  , то матрица
, то матрица 
 , тогда матрица
, тогда матрица 

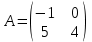
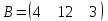
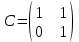
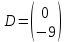
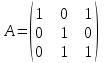
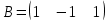
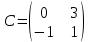
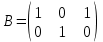
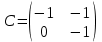
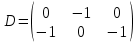
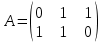
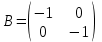
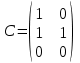
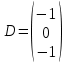
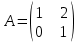
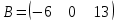
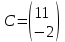
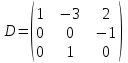
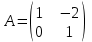
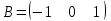
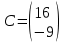
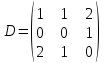
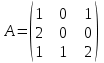
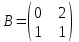
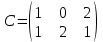
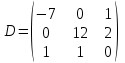
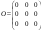 является
является