РП_05.03.06__бак_Математика. 1 Цель и задачи освоения дисциплины Целью освоения дисциплины Математика
 Скачать 1.02 Mb.
|
|
ОПК-1 Способен применять базовые знания фундаментальных разделов наук о Земле, естественно-научного и математического циклов при решении задач в области экологии и природопользования Расчетно-графическая работа Задача 1. Вероятность всхожести семян пшеницы равна  . Какова вероятность того, что из  посеянных семян взойдут не менее  ? Найти наивероятнейшее число всходов среди посеянных семян.1.  ;  ;  . 2.  ;  ;  . 3. ;  ;  . 4. ; ; .5.  ; ; . 6.  ; ; .7. ; ; . 8. ; ; .9. ;  ; . 10. ; ; .11. ; ; . 12. ; ; .13. ; ; . 14. ; ; .15. ; ; . 16. ; ; .17. ; ; . 18. ; ;  .19. ; ; . 20. ; ; .21. ; ; . Задача 2. Вероятность вызревания кукурузного стебля с тремя початками равна . Найти вероятность того, что среди стеблей опытного участкам число таких стеблей будет ровно штук.1.  ;  . 2.  ;  .3.  ;  . 4.  ;  .5. ;  . 6.  ;  .7. ;  . 8. ;  .9. ;  . 10. ;  .11. ;  . 12. ;  .13. ;  . 14. ;  .15. ;  . 16. ;  .17. ;  . 18. ;  .19. ;  . 20. ; .21. ;  . Для промежуточного контроля по компетенции «УК-1 Способен осуществлять поиск, критический анализ и синтез информации, применять системный подход для решения поставленных задач». Вопросы к экзамену: 1. Матрицы: основные понятия. 2. Операции над матрицами. 3. Приложения матриц в эпидемиологии. 4. Понятие определителя. Вычисление определителя 2-го и 3-го порядков. 5. Системы линейных уравнений: основные понятия. 6. Метод Гаусса решения систем линейных уравнений. 7. Метод Крамера решения систем линейных уравнений. 8. Решения систем линейных уравнений с помощью обратной матрицы. 9. Основные задачи аналитической геометрии. 10. Уравнения прямой на плоскости. 11. Угловой коэффициент прямой. Координаты точки пересечения двух прямых. 12. Расстояние между двумя точками на плоскости. Деление отрезка в заданном соотношении. 13. Уравнение окружности, график функции. 14. Уравнение эллипса, график функции. 15. Уравнение параболы, график функции. 16. Уравнение гиперболы, график функции. 17. Способы задания кривых второго порядка в производственных задачах. 18. Предел функции в точке и методы его вычисления. 19. Раскрытие неопределенностей. 20. 1-ый и 2-ой замечательные пределы. 21. Понятие производной. Смыслы производной. 22. Правила дифференцирования. Табличное дифференцирование. 23. Производная сложной функции. Производные высших порядков. 24. Дифференциал функции и его приложение. 25. Приложения производных в задачах биологии. 26. Алгоритм исследования функции на экстремум. 27. Общая схема исследования функции и построение графика. 28. Частные производные функции 2-х переменных. 29. Исследование на экстремум функции двух переменных. 30. Понятие о методе наименьших квадратов. 31. Первообразная функции. Неопределенный интеграл и его свойства. 32. Простейшие приемы интегрирования. 33. Определенный интеграл и его свойства. 34. Формула Ньютона-Лейбница и вычисление определенных интегралов. 35. Приложения определенного интеграла. 36. Несобственные интегралы и их приложения. Практические задания для экзамена
ОПК-1 Способен применять базовые знания фундаментальных разделов наук о Земле, естественно-научного и математического циклов при решении задач в области экологии и природопользования Вопросы к экзамену: 37. Основные понятия теории вероятностей. Классификация событий. 38. Алгебра событий. 39. Классическое и статистическое определения вероятности. 40. Теоремы сложения и умножения вероятностей. 41. Формулы полной вероятности и Байеса. 42. Схема и формула Бернулли. 43. Теорема Пуассона. 44. Локальная теорема Лапласа-Муавра. 45. Интегральная теорема Лапласа-Муавра. 46. Наивероятнейшее число наступления испытаний. 47. Случайные величины: основные понятия. 48. Дискретные случайные величины: основные понятия. 49. Математическое ожидание случайной дискретной величины и его свойства. 50. Дисперсия случайной дискретной величины и ее свойства. 51. Среднее квадратичное отклонение случайной дискретной величины. 52. Непрерывные случайные величины: основные понятия. 53. Интегральная и дифференциальная функции распределения случайной величины. 54. Интегральная функция распределения и ее свойства. 55. Дифференциальная функция распределения и ее свойства. 56. Числовые характеристики случайных непрерывных величин, 57. Нормальный закон распределения. 58. Кривая нормального распределения и ее свойства. 59. Вероятность попадания нормально распределенной величины в заданный интервал. 60. Вероятность отклонения нормально распределенной случайной величины от математического ожидания. 51. Правило «трех сигм». 62. Закон больших чисел. Практические задания для экзамена
|
,
,
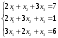
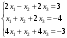
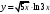
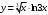
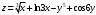
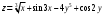
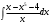
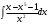
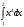
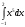
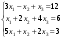
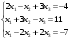
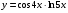
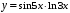
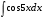
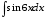
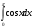
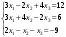
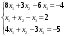
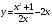
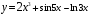
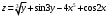
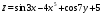
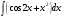
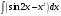
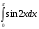
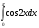
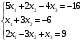
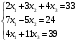
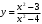
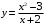
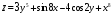
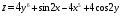
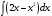
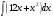
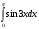
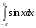
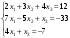
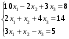
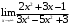
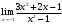
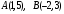
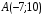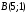