электро часть 1. 1 Цепи постоянного тока 1 Общие положения

• Название: 1 Цепи постоянного тока 1 Общие положения
• Дата: 11.01.2023
• Размер: 3.08 Mb.
• Имя файла: электро часть 1.doc
• Тип: Документы; #880769
• страница: 3 из 11

1.3 Распределение потенциала в простой электрической цепи

Распределение потенциала вдоль неразветвленной электрической цепи можно наглядно представить при помощи графика. Рассмотрим его построение на примере цепи изображенной на рисунке 1.14.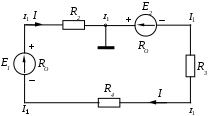



Рисунок 1.14 - Электрическая цепь

Дано: . Точка «а» - «земля».

Найти: потенциальную диаграмму цепи.

Если по оси абсцисс откладывать сопротивление участков, а по оси ординат потенциалы соответствующих точек, то легко получить график распределения потенциала вдоль неразветвленной цепи. Полученная таким методом диаграмма показана на рисунке 1.15.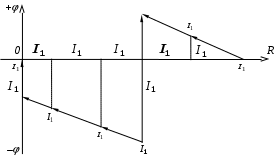



Рисунок 1.15 - Потенциальная диаграмма

Пользуясь этим графиком, можно определить напряжения между двумя любыми точками цепи.

График распределения потенциала внутри источника энергии может иметь разный вид. В простейшем случае - это линейная зависимость.

1.4 Баланс мощности в электрической цепи

Р 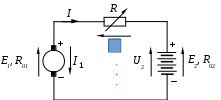ассмотрим энергетический баланс в электрической цепи. Пусть задана цепь вида,

Рисунок 1.16 - К балансу мощности

Дано:

Найти: Составить баланс.

После расстановки стрелок тока и напряжения по второму закону Кирхгофа электрическое состояние цепи запишется

отсюда .

Умножим обе части равенства на ток , получим

.

Следовательно,

- мощность генерируемая в цепи.

- потребляемая энергия. Таким образом . (1.8)

По закону сохранения энергии количество вырабатываемой в цепи энергии всегда равно количеству энергии потребляемой цепью. Следует всегда помнить, при составлении баланса энергии в цепи, что не всякий источник энергии, действующий в цепи является генератором, а именно: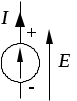


Когда действительный ток через источник совпадает по направлению с ЭДС источника, то этот источник вырабатывает энергию, то есть является генератором.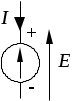


Когда действительный ток через источник протекает навстречу ЭДС источника, то этот источник потребляет энергию, то есть является нагрузкой (пример: зарядка аккумулятора).

1.5 Законы Кирхгофа

Законы Кирхгофа являются основными расчетными законами электротехники. Закон Ома частный случай законов Кирхгофа.

До сих пор мы рассматривали простые или неразветвленные цепи. Эти цепи решаются с помощью закона Ома.

Сложные или разветвленные цепи рассчитываются при помощи законов Кирхгофа.

Сложной или разветвленной цепью называют такая, в которой имеется несколько путей для растекания токов (см. рисунок 1.17).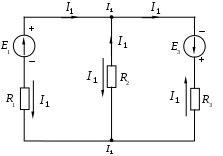




Рисунок 1.17 - Сложная цепь постоянного тока
Точки разветвления цепи А и Б - узлы цепи.

Узлами называются точки цепи, в которых соединяются между собой три или более проводников.

Проводники, соединяющие между собой узлы, называются ветвями.

Ветви бывают двух видов:

1. 
   активные,
   
2. 
   пассивные.
   

Активной ветвью называется такая ветвь, которая содержит не только сопротивления, но и источники энергии.

Пассивной ветвью называется такая ветвь, которая содержит только сопротивления, но не содержит источников энергии.

Таким образом, сложная цепь состоит из узлов и ветвей, то есть из 2-х элементов, поэтому и законов Кирхгофа два. Первый закон Кирхгофа управляет узлами, а второй - ветвями (контурами).

Первый закон Кирхгофа гласит:

В любом узле сложной цепи алгебраическая сумма токов равна нулю.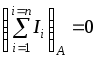
, (1.9)
где i - количество токов связанных с рассматриваемым узлом;

А - обозначение рассматриваемого узла.

Первый закон основан на принципе невозможности накопления электрического заряда в одной точке цепи.

Принято токи, притекающие к узлам цепи, считать положительными и брать со знаком плюс, а токи, оттекающие от узлов, считать отрицательными и брать со знаком минус.

Запишем первый закон Кирхгофа для узлов А и Б нашей цепи (рисунок 1.17).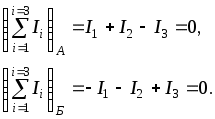

(1.10)

Сравнивая уравнения между собой, видим, что одно из них является следствием другого. Поэтому в цепи выделяют узлы называемыми независимыми.

Независимыми узлами называют такие, которые отличаются друг от друга, хотя бы одним током.

Число независимых уравнений, составляемых по первому закону Кирх­­гофа, равно числу независимых узлов в сложной цепи и равно общему числу узлов в цепи без одного.

Число независимых узлов = , (1.11)

где - общее число узлов сложной цепи.

Ветви сложной цепи, образуют контура.

Второй закон Кирхгофа гласит:

В любом контуре сложной цепи алгебраическая сумма ЭДС и нап­ря­же­ний действующих в этом контуре равна нулю.
(1.12)
где i – количество источников ЭДС в рассматриваемом контуре;

k – количество напряжений входящих в данный контур.

Данная формулировка справедлива, если стрелки напряжений на схеме цепи расставлены против стрелок токов.

Примечание:

В некоторых литературных источниках, стрелки напряжений направляются согласно стрелкам тока. Это допустимо, если использовать необходимую в данном варианте формулировку второго закона Кирхгофа:

В любом контуре сложной цепи, алгебраическая сумма ЭДС всегда равна алгебраической сумме напряжений действующих в этом контуре.

. (1.13)

Второй закон Кирхгофа записывается только для независимых контуров.

Независимыми контурами сложной цепи называются такие, которые отличаются друг от друга хотя бы одним элементом цепи не использованным в ранее намеченных контурах.

Число независимых уравнений, составленных по второму закону Кирхгофа, равно числу независимых контуров в цепи.

Число уравнений по 2-му закону Кирхгофа = , (1.14)

где - общее число ветвей всей цепи.

При обходе по контуру стрелки ЭДС и напряжений, совпадающие с направлением обхода, берутся со знаком плюс, встречно направленные - со знаком минус.

Запишем уравнения электрического состояния контура (см. рисунок 1.17) по второму закону Кирх­гофа:

а) при обходе слева направо



б) при обходе справа налево

.

Следовательно, направление обхода контуров можно выбирать произвольно.

Законы Кирхгофа позволяют рассчитывать самые сложные цепи.