электро часть 1. 1 Цепи постоянного тока 1 Общие положения

• Название: 1 Цепи постоянного тока 1 Общие положения
• Дата: 11.01.2023
• Размер: 3.08 Mb.
• Имя файла: электро часть 1.doc
• Тип: Документы; #880769
• страница: 9 из 11

1.8.4 Общие замечания о четырехполюсниках

Часть электрической цепи произвольной конфигурации, имеющая два входных зажима для присоединения источника энергии и два выходных зажима для присоединения нагрузки называется четырехполюсником.

Четырехполюсники бывают активные и пассивные.

Четырехполюсник, не содержащий внутри себя источников энергии, называется пассивным. Он обозначается прямоугольником и буквой «П», см. рисунок 1.54.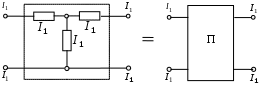


Рисунок 1.54 - Пассивный четырехполюсник

Четырехполюсник, содержащий внутри себя источники энергии, называется активным. Он обозначается прямоугольником и буквой «А», см. рисунок 1.55.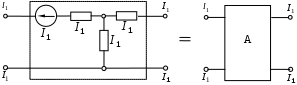


Рисунок 1.55 - Активный четырехполюсник

1.8.5 Основные уравнения пассивного четырехполюсника

Рассмотрим основы теории пассивных четырехполюсников. Пусть нам задан четырехполюсник, изображенный на рисунке 1.56.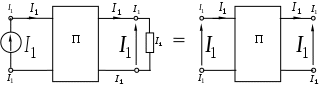



Рисунок 1.56 - Пассивный четырехполюсник

Здесь: зажимы 1-1 - называются входными или первичными;

зажимы 2-2 - называются выходными или вторичными;

ток, напряжение и мощность: - называются входными;

ток, напряжение и мощность: - называются выходными.

Сопротивление, замеренное с зажимов 1-1, называется входным или первичным.

Сопротивление, замеренное с зажимов 2-2, называется выходным или вторичным.

З 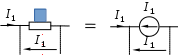аписав на выходных зажимах, мы произведем эквивалентную замену сопротивления на источник ЭДС, который противодействует току в такой же мере, как и сопротивление .
Рисунок 1.57 - Эквивалентная замена

Таким образом, в нашей схеме теперь два источника ЭДС. По методу наложения уравнения для токов запишутся:

(1.119)

Отрицательные знаки перед получились вследствие того, что и действуют на встречу друг другу.

Выразим входное напряжение , а так же ток через выходные величины. Из уравнения (1.119) имеем

. (1.120)

Подставим (1.120) в первое соотношение (1.119), получим

. (1.121)

В результате будем иметь систему: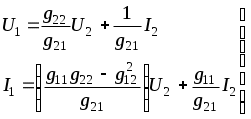

. (1.122)

Введем обозначения:

- коэффициент (нулевая размерность);

- коэффициент (размерность сопротивления);

- коэффициент (размерность проводимости);

- коэффициент (нулевая размерность).

Подставляем коэффициенты 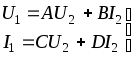в систему (1.122):

. (1.123)

Система (1.123) называется основными уравнениями пассивного четырехполюсника.

Основными уравнениями пассивного четырехполюсника называются урав­не­ния, связывающие напряжение и ток на входе четырехполюсника с напряжением и током на выходе.

- называются коэффициентами или постоянными четырехполюсника.

Из полученных выражений можно сделать вывод.

Постоянные четырехполюсника зависят только от сопротивлений, проводимостей и конфигурации цепи.

В этом мы убедимся на примерах. Рассмотрим некоторые зависимости между коэффициентами четырехполюсника.

1. 
   Вычислим определитель из коэффициентов, .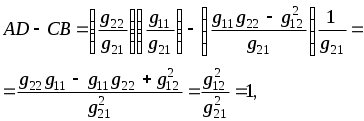
   

(1.124)

.

Определитель из коэффициентов пассивного четырехполюсника всегда равен единице.

Это основное свойство коэффициентов пассивного четырехполюсника.

2. 
   Поменяем местами источник энергии и нагрузку четырехполюсника, изоб­раженного на рисунке 1.56.
   

Основные уравнения в этом случае будут иметь вид: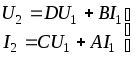

. (1.125)

Отсюда следует весьма важное свойство:

При замене первичных зажимов вторичными, коэффициенты и меняются местами на главной диагонали.

Четырехполюсники бывают двух видов:

1. 
   симметричные; 2) несимметричные.
   

Четырехполюсник называется симметричным, если при перемене местами источника энергии и нагрузки, токи источника и нагрузки остаются неизменными.

Уравнения симметричного четырехполюсника остаются неизменными при взаимной замене первичных и вторичных зажимов.

Поэтому, в симметричном четырехполюснике коэффициенты на главной диагонали всегда равны друг другу: .

Пассивный четырехполюсник называется несимметричным, если при перемене местами источника и приемника энергии, токи их изменяются.

Симметричный четырехполюсник является частным случаем несимметричного.