электро часть 1. 1 Цепи постоянного тока 1 Общие положения
 Скачать 3.08 Mb. Скачать 3.08 Mb.
|
1.7 Методы расчета сложных цепейВ зависимости от конфигурации и условий заданной цепи применяются для расчета цепи различные методы. Однако все методы расчета основаны на законах Кирхгофа. Искусство расчетчика состоит в том, что он находит наиболее рациональный метод решения к конкретно заданной цепи. Рассмотрим наиболее употребительные методы расчета цепей. 1.7.1 Метод линейных преобразованийДанный метод основан на использовании закона Ома и формул последовательного, параллельного, смешанного соединения сопротивлений, а также перехода от соединения сопротивлений в треугольник к звезде. Сначала сложная цепь свертывается до предельно простой и решается по закону Ома – прямой путь. Затем, полученное решение развертывается до заданной конфигурации цепи – обратный путь. Основное условие применимости метода – в цепи должен быть только один источник питания. Дано: цепь, показанная на рисунке 1.24; параметры Е, R1, R2, R3, R4, R5, R6. 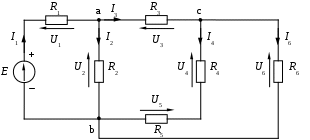 Рисунок 1.24 – Исходная схема цепи Найти 1. Эквивалентное сопротивление всей цепи относительно зажимов источника питания. 2. Все токи. 3. Проверить полученные результаты на: а) баланс токов, б) баланс мощности. 4. Напряжения на всех элементах цепи. 5. Проверить напряжения на баланс напряжений. Порядок расчета Расставляем на исходной схеме стрелки токов. Поскольку в схеме только один источник энергии токи можно разметить сразу в правильном направлении. Токов будет столько, сколько ветвей в цепи. Стрелки токов размечают непосредственно на проводниках. 2. Размечаем стрелки напряжений. Напряжения расставляются на каждом элементе цепи. Направление стрелок напряжений всегда выбирается против токов текущих в ветви. 3. Определяем эквивалентное сопротивление всей цепи относительно зажимов источника питания. Свертываем цепь (прямой путь). Первое преобразование (показано на рисунке 1.25). 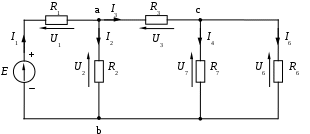 Рисунок 1.25 – Расчетная схема после первого преобразования П 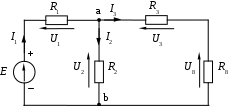 роводим второе преобразование цепи (схема показана на рисунке 1.26). роводим второе преобразование цепи (схема показана на рисунке 1.26).Рисунок 1.26 – Расчетная схема после второго преобразования Третье преобразование (см. рисунок 1.27). 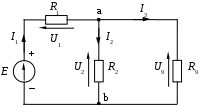 Рисунок 1.27 – Расчетная схема после третьего преобразования Четвертое преобразование (см. рисунок 1.28). Р 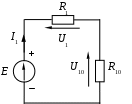 исунок 1.29 – Расчетная схема после четвертого преобразования исунок 1.29 – Расчетная схема после четвертого преобразованияПоследнее, пятое преобразование (см. рисунок 1.30). 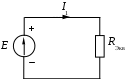 Рисунок 1.30 – Расчетная схема после пятого преобразования Определяем ток 4. Развертываем решение (обратный путь) и находим токи в ветвях цепи. Воспользовавшись схемой изображенной на рисунке 1.27, найдем токи Переходя к рисунку 1.25, определяем токи Токи Согласно второму закона Кирхгофа имеем 5. Проверка полученных результатов. а) Баланс токов. Из рисунка 1.25 следует: б) Баланс мощности. Мощность вырабатываемая генератором Мощность нагрузки 6. Определяем напряжения на всех участках цепи. Делаем это по закону Ома: 7. Проверяем напряжения на баланс напряжений. Для этого, составим уравнения по второму закону Кирхгофа для цепи изображенной на рисунке 1.25. Первое уравнение Второе уравнение Третье уравнение Если балансы тока, напряжения и мощности сошлись с погрешностью не более 1%, то расчет считается выполненным правильно. 1.7.2 Метод законов КирхгофаРассмотрим расчет сложной цепи методом законов Кирхгофа. Для схемы, приведенной на рисунке 1.31, дано: Е1; Е3; R1; R2; R3. 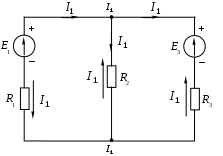 Рисунок 1.31 - Расчетная схема Найти 1. Все токи. 2. Проверить полученные результаты на баланс токов и баланс мощности. 3. Напряжения на всех элементах цепи. 4. Проверить напряжения на баланс напряжений. Порядок расчета Размечаем токи. Как и ранее, токи размечаются стрелками непосредственно на проводах схемы. Стрелки токов направляются в произвольном направлении. Неизвестных токов будет столько, сколько имеется ветвей в сложной цепи. Индекс тока принимается равным индексу ветви. 2. Размечаем стрелки напряжений на элементах цепи. Стрелки расставляем не произвольно, а всегда против ранее размеченных стрелок токов. Произвольно стрелки напряжений размечать нельзя. Составляем уравнения электрического состояния цепи. Для решения нашей задачи требуется система из трех уравнений. По первому закону Кирхгофа число уравнений будет По второму закону Кирхгофа число уравнений будет Имеем: 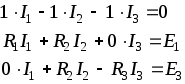 . (1.58) . (1.58)Решаем систему уравнений. При решении уравнений можно использовать вычислительную технику или производить данную операцию вручную. В данном случае применим метод определителей (метод Крамера). Имеем: 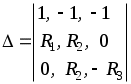 ; ; 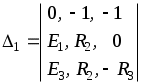 ; ;(1.59) 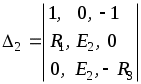 ; ; 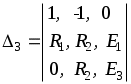 . .Тогда токи будут равны: Проверяем полученный результат на баланс токов. Проверка производится во всех независимых узлах сложной цепи по первому закону Кирхгофа. Проверяем полученный результат на баланс мощности. По закону сохранения энергии количество выработанной в цепи и потребленной энергии должны быть равны. Выработано Израсходовано При правильном значении токов Непосредственное применение законов Кирхгофа к расчету сложной цепи приводит к весьма громоздким вычислениям, так как приходится решать систему с большим числом уравнений. Поэтому, этот метод на практике применяется крайне редко из за его неэкономичности. 1.7.3 Метод контурных токовМетод контурных токов был предложен известным английским физиком и электротехником Джеймсом К. Максвеллом. По этому методу цепь разбивается на ряд контуров, соприкасающихся друг с другом. Число контуров подсчитывается по формуле (1.14). Предполагается, на время расчета, что каждый контур обтекается только присущим ему током, который называется контурным током. Контурный ток - нереальный ток, он является вспомогательным средством при решении цепей. Контурных токов столько, сколько имеется в цепи независимых контуров. Контуров в цепи всегда меньше числа ветвей, так как, даже для простого контура требуется, по крайней мере, две ветви. Указанное обстоятельство приводит к тому, что контурных токов в цепи всегда меньше числа реальных токов. Таким образом, основное преимущество метода контурных токов перед методом законов Кирхгофа состоит в сокращении числа расчетных уравнений. По известным контурным токам, действительные токи определяются простым алгебраическим сложением. Рассмотрим порядок расчета цепи указанным методом. Для цепи, изображенной на рисунке 1.32, дано: Е1; Е3; R1; R2; R3. 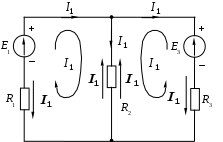 Рисунок 1.32 - Расчетная схема Найти 1. Все токи. 2. Проверить полученные результаты на баланс токов и баланс мощности. 3. Напряжения на всех элементах цепи. 4. Проверить напряжения на баланс напряжений. Порядок расчета Размечаем контурные токи. Направление токов выбирается произвольно, однако, где это возможно, желательно в смежных ветвях иметь их сумму. Размечаем стрелки напряжений. Стрелки напряжений расставляют по общему правилу, то есть всегда против ранее размеченных контурных токов. Стрелки напряжений снабжаются двумя индексами. Первый индекс - номер элемента, второй - номер контурного тока. Составляем уравнения электрического состояния цепи. Для этого обходим каждый контур в произвольном направлении и составляем уравнения по второму закону Кирхгофа 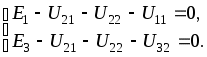 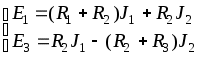 . (1.61) . (1.61)Решаем уравнения электрического состояния цепи. Решение, как и ранее, проводим с помощью определителей: 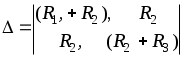 ; ; 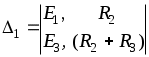 ; (1.62) ; (1.62)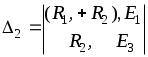 . . Отсюда: Размечаем действительные токи в цепи. Действительные токи можно направлять произвольно, однако, лучше учитывать при разметке направления и значения контурных токов, через которые они определяются. Стрелки действительных токов показаны на рисунке 1.32. Определяем действительные токи. Для этого имеем: 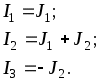 (1.64) (1.64)Проверяем значения токов на баланс токов. Проверку производим в каждом узле цепи по первому закону Кирхгофа Проверяем значения токов на баланс мощности Метод контурных токов получил широкое распространение в инженерной практике, благодаря экономным затратам времени на расчет. 1.7.4 Метод наложения (суперпозиции)Метод основан на принципе Д’Аламбера - независимости действия сил на линейную систему. Проиллюстрируем принцип Д’Аламбера, рисунком 1.33.  Рисунок 1.33 - К принципу Д’Аламбера В электрической цепи вместо сил используют ЭДС цепи. Схему решают столько раз, сколько имеется в цепи источников энергии. Результаты решения алгебраически суммируют. Применим метод к нашей цепи. 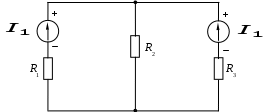 Для цепи, изображенной на рисунке 1.32, дано: Е1; Е3; R1; R2; R3;RО1; RО2. Для цепи, изображенной на рисунке 1.32, дано: Е1; Е3; R1; R2; R3;RО1; RО2.Рисунок 1.34 - Расчетная схема Найти 1. Все токи. 2. Проверить полученные результаты на баланс токов и баланс мощности. 3. Напряжения на всех элементах цепи. Порядок расчета Составляем расчетные подсхемы. Расчетных подсхем будет столько же, сколько имеется в цепи источников энергии. В нашем случае - мы имеем две расчетных подсхемы, показанные на рисунке 1.35. Их алгебраическая сумма - есть исходная цепь. 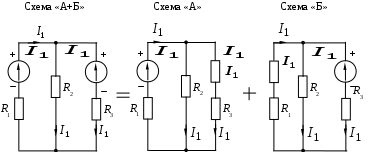 Рисунок 1.35 - Подсхемы цепи Размечаем токи на подсхеме «А». Токи можно разметить сразу правильно, так как в цепи имеется лишь один источник. Токи размечаем с индексами «», см. рисунок 1.35. Решаем схему «А». Решение можно производить любым методом, который обеспечивает самое короткое решение. В результате, получаем токи: Размечаем токи на подсхеме «Б». И здесь во многих случаях токи можно разметить сразу правильно, так как в цепи действует лишь один источник энергии. Токи размечаются с индексами «», см. рисунок 1.35. Решаем подсхему «Б». Решение можно производить любыми методом, который обеспечивает самое короткое решение. В результате получаем токи: 6. Размечаем токи на главной схеме «А+Б» Токи на главной схеме можно разметить произвольно. Однако, лучше учитывать при этом величины токов, полученных решением подсхем, см. рисунок 1.35. 7. Определяем значения действительных токов. На основании нашей разметки имеем: 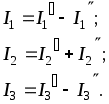 . (1.67) . (1.67)Проверяем действительные токи на баланс токов. Проверку производим во всех узлах по первому закону Кирхгофа Проверяем действительные токи на баланс мощности в цепи Указанный метод получил распространение в инженерной практике, особенно он часто он применяется тогда, когда необходимо знать долевое участие каждого источника энергии в питании всей электрической цепи. 1.7.5 Метод узловых потенциаловМетод узловых потенциалов основан на первом законе Кирхгофа и на законе Ома. Преимущество метода состоит в том, что он позволяет сократить число расчетных уравнений и тем самым уменьшить вычислительную работу. Для выяснения сущности метода рассмотрим электрическую цепь, показанную на рисунке 1.36. 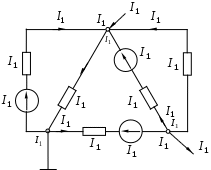 Рисунок 1.36 - К методу узловых потенциалов Соединим один из узлов с землей, то есть придадим этому узлу нулевой потенциал земли. Такое допущение не влияет на работу цепи и не изменит токов в ветвях, так как величина токов определяется не потенциалами узлов, а разностью потенциалов между узлами, к которым присоединены ветви. Узловым потенциалом называется потенциал узла сложной цепи относительно узла, потенциал которого принят равным нулю. Размечаем произвольно потенциалы узлов 1 и 2 и токи в ветвях цепи. По первому закону Кирхгофа для незаземленных узлов будем иметь 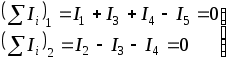 . (1.70) . (1.70)Токи в ветвях определяются по закону Ома: где Подставляя (1.71) в (1.70), будем иметь: 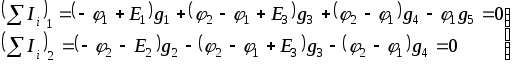 ; (1.72) ; (1.72)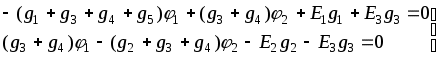 . (1.73) . (1.73)Введем обозначения: 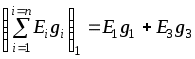 (1.74) (1.74) - алгебраическая сумма произведений ЭДС на соответствующие проводимости, примыкающие к узлу 1 цепи; 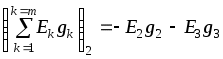 (1.75) (1.75)- то же, но примыкающая к узлу 2 цепи. Произведение ЭДС на проводимость берут со знаком плюс, если стрелка ЭДС источника направлена к рассматриваемому узлу и минус, если она направлена от узла. Сумма проводимостей ветвей, присоединенных к узлам 1 и 2, запишется так: Величины Сумма проводимостей ветвей, соединяющих узлы 1 и 2, записывается так: В дальнейшем будем называть Подставим (1.74), (1.75), (1.76), (1.77) в (1.73): 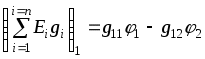 ; ;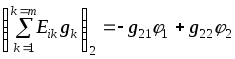 . (1.78) . (1.78)Если в цепи действует не только ЭДС, но и источник тока, то эти токи следует учесть в левых частях уравнений (1.78). Токи « Положим, что В результате получим: 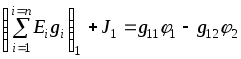 ; ;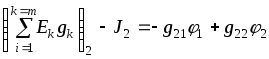 . (1.79) . (1.79)Если электрическая цепь имеет в своем составе 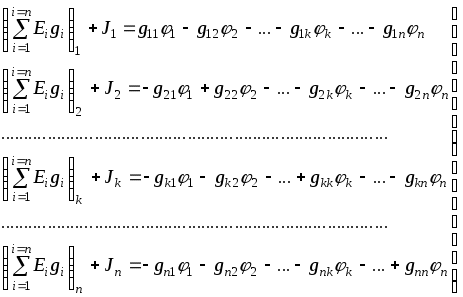 . (1.80) . (1.80)Решая систему (1.80) относительно Применим изложенный метод к сложной цепи, изображенной на рисунке 1.36. Для цепи, изображенной на рисунке 1.32, дано: Е1; Е4; R1; R2; R3;R4; R5;R6. Найти 1. Все токи. 2. Проверить полученные результаты на баланс токов и баланс мощности. 3. Напряжения на всех элементах цепи. 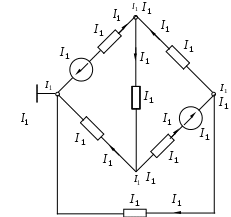 Рисунок 1.32 - Расчетная схема Порядок расчета Заземляем один из узлов цепи. Заземлению можно подвергнуть любой из четырех узлов цепи. Обозначаем потенциал заземленного узла через «0». Размечаем цифрами незаземленные узлы. Разметку узлов можно производить в произвольном порядке. Размечаем потенциалы незаземленных узлов. На схеме это - Определяем проводимости всех ветвей цепи: Составляем уравнения узловых потенциалов. 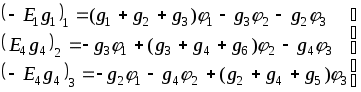 . (1.82) . (1.82)Примечание: Если в цепи имеется ветвь с ЭДС ( Решаем систему уравнений узловых потенциалов. Решение производим методом определителей, или используя вычислительную технику: Размечаем стрелки действительных токов на ветвях цепи. Стрелки токов можно размечать как обычно, то есть произвольно. 8. Определяем величины действительных токов в ветвях цепи. Для определения токов используем значения ранее вычисленных потенциалов узлов и закон Ома: 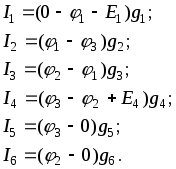 . (1.84) . (1.84)Поверяем действительные токи на баланс токов Проверку производим во всех независимых узлах цепи по первому закону Кирхгофу. Проверяем действительные токи на баланс мощности 1.7.5.1 Метод узлового напряженияВ заключение, применим метод узловых потенциалов к цепи частного вида, когда в ней имеется всего два узла и Для цепи, изображенной на рисунке 1.33, дано: Е1; Е2; ... En; R1; R2; ... Rn. Найти - все токи методом узловых потенциалов. 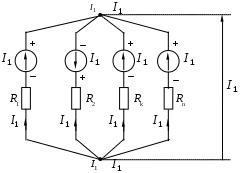 Рисунок 1.33 - Расчетная схема Составляем уравнение по методу узловых потенциалов. Поскольку здесь только один независимый узел, то уравнение также будет только одно. 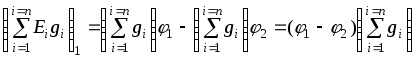 , но , но 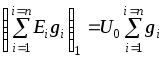 отсюда получаем выражение для определения узлового напряжения, отсюда получаем выражение для определения узлового напряжения,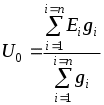 . (1.86) . (1.86)Узловым напряжением называется напряжение между двумя узлами цепи. Токи в ветвях найдутся весьма просто по известному узловому напряжению, а именно: 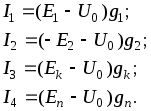 . (1.87) . (1.87)Чтобы механически пользоваться формулой (1.87), следует выполнять два правила: - полагают один из узлов (любой) положительным и к нему направляют все токи ветвей; - стрелку узлового напряжения, также направляют к выбранному положительному узлу. Чтобы токи в ветвях были рассчитаны правильно, необходимо с большой точностью находить величину узлового напряжения. В этом один из крупных недостатков метода узлового напряжения. Указанный метод получил весьма широкое применение в расчетной практике благодаря своей экономичности в вычислительной работе. 1.7.6 Метод эквивалентного генератора (метод теоремы Тевенена -Гельмгольца)Метод эквивалентного генератора позволяет определить один ток в сложной цепи без расчета всех остальных токов. Рассмотрим теорию этого метода. Пусть нам дана схема, показанная на рисунке 1.34. Проведем преобразования указанные на рисунке. В результате имеем, что ток в где В 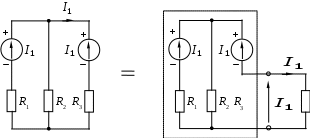 ыражение (1.88) носит название - теорема Тевенена-Гельмгольца. ыражение (1.88) носит название - теорема Тевенена-Гельмгольца.Рисунок 1.34 - К методу эквивалентного генератора 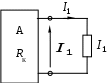 Рисунок 1.35 - Эквивалентный генератор Эквивалентная схема цепи полученная в результате преобразований исходной схемы изображена на рисунке 1.35. Рассмотрим применение метода эквивалентного генератора к расчету тока в цепи. Д 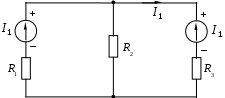 ля цепи, изображенной на рисунке 1.36, дано: Е1; Е3; R1; R2; R3. ля цепи, изображенной на рисунке 1.36, дано: Е1; Е3; R1; R2; R3.Найти - ток Рисунок 1.36 - Исходная схема Порядок расчета Составляем расчетную схему для определения ЭДС эквивалентного генератора. 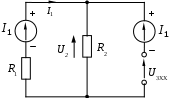 Рисунок 1.37 - Режим холостого хода Для этого, устраиваем режим холостого хода в третьей ветви, то есть размыкаем ветвь и убираем из ветви сопротивление, см. рисунок 1.37. Если ветвь активная, то ЭДС ветви должна быть оставлена, исключается только сопротивление ветви. Холостой режим нужен потому, что при нем напряжение на зажимах ветви равно ЭДС на этих же зажимах. Определим ЭДС эквивалентного генератора. Для определения ЭДС можно воспользоваться любым методом к расчету схемы: Составляем расчетную схему для определения внутреннего сопротивления генератора 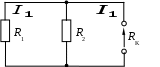 Рисунок 1.38 - Режим короткого замыкания Чтобы определить внутреннее сопротивление эквивалентного генератора составляем расчетную схему всей цепи относительно клемм При составлении схемы следует иметь ввиду, что все ЭДС цепи полагаются равными нулю. Если ЭДС имеют внутреннее сопротивление R0, то они должны быть оставлены. Определяем внутреннее сопротивление эквивалентного генератора. Расчет сопротивления производится по расчетной схеме для режима короткого замыкания. В нашем случае Определяем ток в 3-й ветви. Для этого используем теорему Тевенена-Гельмгольца. 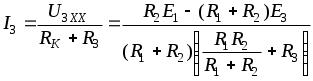 . (1.92) . (1.92)Указанный метод имеет широкое применение в расчетной практике во всех случаях, когда требуется отыскать лишь один ток в сложной цепи. 1.7.7 Метод теоремы ПоливановаМетод теоремы К. М. Поливанова так же, как и метод эквивалентного генератора позволяет определять только один ток в сложной цепи. В противоположность теореме Тевенена-Гельмгольца здесь используется не режим холостого хода, а режим короткого замыкания ветви, в которой отыскивается ток. Рассмотрим теорию данного метода. Согласно теореме об эквивалентном генераторе (см. рисунок 1.35) имеем 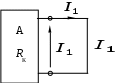 Рисунок 1.39 - К методу Поливанова Разделим числитель и знаменатель выражения (1.93) на 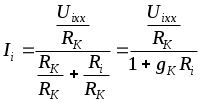 . (1.94) . (1.94)Числитель выражения (1.94) представляет собой ток короткого замыкания эквивалентного генератора Подставляя (1.95) в (1.94) получим где Выражение (1.96) называется теоремой Поливанова. Рассмотрим применение теоремы Поливанова к отысканию тока в сложной цепи. Для цепи, изображенной на рисунке 1.40, дано: Е1; Е3; R1; R2; R3. Найти - ток 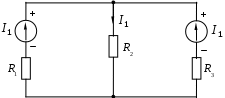 Рисунок 1.40 - Исходная схема Порядок расчета Составляем расчетную схему для отыскания тока короткого замыкания во второй ветви, (рисунок 1.41). Р 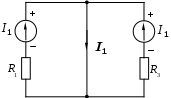 исунок 1.41 - Режим холостого хода исунок 1.41 - Режим холостого ходаДля этого, закорачиваем сопротивление второй ветви. Если ветвь активная, то закорачиванию подлежит только сопротивления, а источник энергии в ветви должен быть оставлен. Определим величину тока короткого замыкания во второй ветви. Расчет производится по расчетной схеме любыми методами, дающими самое короткое решение. В нашем случае имеем 3. Составляем расчетную схему для определения проводимости цепи  R3 Рисунок 1.42 - Режим короткого замыкания При составлении схемы все ЭДС источников полагают равными нулю, внутренние сопротивления источников оставляют в схеме. Схема показана на рисунке 1.42. Определяем величину Определяем величину тока Для этого записываем теорему Поливанова 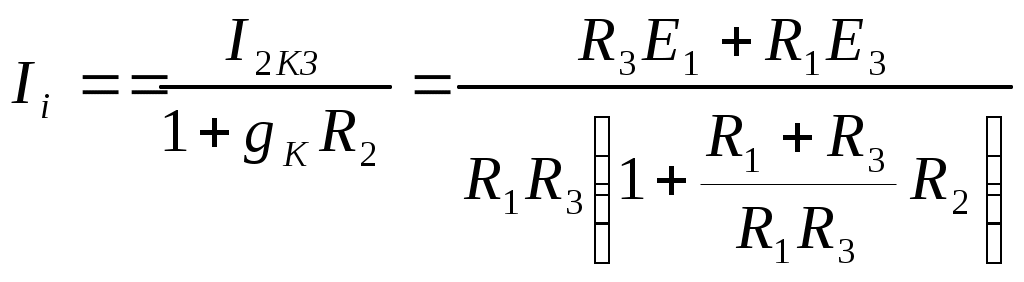 . (1.99) . (1.99)Метод широко применяется на практике. 1.7.8 Свойство взаимностиСущность свойства взаимности или принципа взаимности состоит в следующем. П 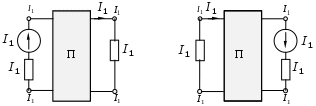 усть в схеме любой сложности (см. рисунок 1.43) имеется единственный источник ЭДС, действующий от зажима 2 к зажиму 1 в ветви К. усть в схеме любой сложности (см. рисунок 1.43) имеется единственный источник ЭДС, действующий от зажима 2 к зажиму 1 в ветви К.Рисунок 1.43 - К принципу взаимности Пусть эта ЭДС вызывает ток Если ЭДС из ветви К перенести в ветвь Таким образом токи и ЭДС ветвей взаимно перемещаются, как показано на рисунке 1.44. Указанное свойство является принципом взаимности. Проиллюстрируем свойство взаимности следующим примером. Пусть нам дана цепь, показанная на рисунке 1.44. 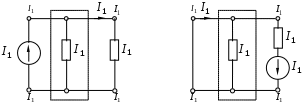 Схема «А» Схема «Б» Рисунок 1.44 - Пример использования принципа взаимности Для схемы «А» имеем Для схемы «Б» имеем Принцип взаимности широко используется при расчете линейных цепей. |
