электро часть 1. 1 Цепи постоянного тока 1 Общие положения
 Скачать 3.08 Mb. Скачать 3.08 Mb.
|
1.6 Преобразования линейных электрических схем1.6.1 Общие замечанияРасчет сложной цепи может быть значительно облегчен путем эквивалентного преобразования электрических схем. Целесообразное преобразование обеспечивает: уменьшение числа узлов в схеме (числа «n»); уменьшение числа ветвей в схеме (числа «g»). Указанное, сокращает число расчетных уравнений. Преобразование схемы имеет две задачи: свернуть цепь к простой и простыми способами получить решение этой задачи; развернуть полученное решение до первоначально заданной схемы. Известно, что электрические цепи можно соединить между собой только тремя способами: а) последовательно; б) параллельно; в) смешано. Рассмотрим данные соединения подробнее. 1.6.2 Последовательное соединение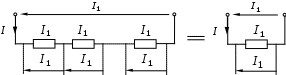 Рисунок 1.18 - Последовательное соединение Последовательным соединением называется такое при котором через все элементы цепи проходит один и тот же ток. Согласно схемы имеем: При последовательном соединении сопротивлений общее сопротивление всегда равно их сумме. Рассмотрим, как распределяются напряжения по элементам: На последовательно соединенных сопротивлениях напряжения распределяется прямо пропорционально сопротивлениям. 1.6.3 Параллельное соединение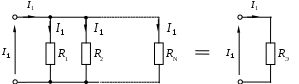 Рисунок 1.19 - Параллельное соединение Параллельным соединением сопротивлений называется такое соединений, при котором все сопротивления находятся под воздействием одного и того же напряжения. Согласно схемы имеем: При параллельном соединении сопротивлений складываются величины, обратные сопротивлениям то есть, проводимости. При параллельном соединении общая проводимость всегда равна сумме проводимостей всех ветвей. Рассмотрим два наиболее часто встречающихся на практике случая параллельного соединения. а) Параллельное соединение n одинаковых сопротивлений. Согласно (1.17), имеем: Общее сопротивление n одинаковых, параллельно соединенных сопротивлений, в n раз меньше сопротивления одной ветви, а общая проводимость в n раз больше проводимости одной ветви. б) Параллельное соединение двух сопротивлений. Согласно (1.17), имеем: Общее сопротивление двух параллельных ветвей всегда равно произведению сопротивлений на сумму сопротивлений этих ветвей. Рассмотрим, как распределяются токи в двух ветвях: Или В параллельных ветвях токи обратно пропорциональны сопротивлениям или прямо пропорциональны проводимостям ветвей. 1.6.4 Смешанное соединение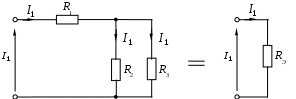 Рисунок 1.20 - Смешанное соединение сопротивлений Смешанным соединением сопротивлений называется такое соединение, при котором действуют одновременно и параллельное и последовательное соединение. С 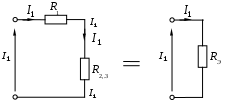 огласно схеме имеем огласно схеме имеемРисунок 1.21 - Промежуточное преобразование смешанного соединения Отсюда найдем токи: В результате преобразования удалось решить разветвленную цепь простыми средствами, в нашем случае, даже без составления уравнений. Следует иметь в виду, что при преобразовании схемы, состоящей только из сопротивлений (ветви не имеют источников энергии), мощность в эквивалентной схеме равна мощности в заданной неразветвленной цепи. 1.6.5 Преобразование «треугольника сопротивлений» в «звезду сопротивлений»Впервые данное преобразование осуществлено итальянским ученым Кеннели. С 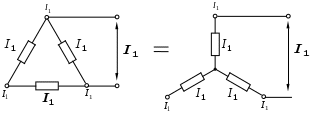 оставляем расчетную схему. оставляем расчетную схему.Рисунок 1.22 - Преобразование «» сопротивлений в «» Для треугольника сопротивлений дано: Найти: Уравнения перехода от треугольника к звезде сопротивлений запишутся: 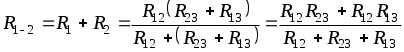 ; (1.26) ; (1.26)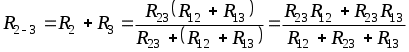 ; (1.27) ; (1.27)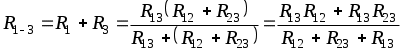 . (1.28) . (1.28)Решим полученную систему относительно неизвестных Откуда получаем аналогично имеем: Выражения (1.30) позволяет определить сопротивления лучей звезды по заданным сопротивлениям сторон треугольника. В частом случае, при симметричном треугольнике, когда все сопротивления сторон треугольника одинаковы, Согласно выражений (1.30), получаем: Луч симметричной звезды всегда равен одной трети сопротивления стороны симметричного треугольника. 1.6.6 Преобразование «звезды сопротивлений» в «треугольник сопротивлений»Р 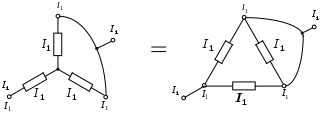 ассмотрим, теперь обратное преобразование. ассмотрим, теперь обратное преобразование.Рисунок 1.23 - Преобразование звезды в треугольник сопротивлений Для звезды сопротивлений дано: Найти:. Согласно схеме, на рисунке 1.23, будем иметь: 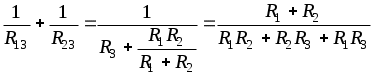 ; (1.32) ; (1.32)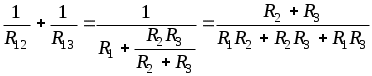 ; (1.33) ; (1.33)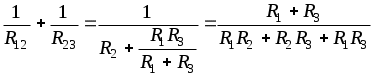 . (1.34) . (1.34)Решаем полученную систему. Для этого сложим (1.33) с (1.34) и вычтем (1.32). Откуда имеем Аналогично получаем: Выразив из (1.35) сопротивления лучей звезды окончательно запишем: Эти же соотношения в проводимостях можно записать так 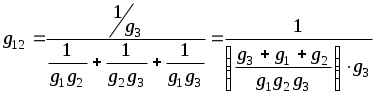 , откуда получим , откуда получимАналогично получаем остальные проводимости: Для симметричного случая, на основании выражения (1.31) имеем |
