Ответы по Методам Исследования. 1. двухзондовый метод
 Скачать 4.56 Mb. Скачать 4.56 Mb.
|
|
1. 2. ДВУХЗОНДОВЫЙ МЕТОД 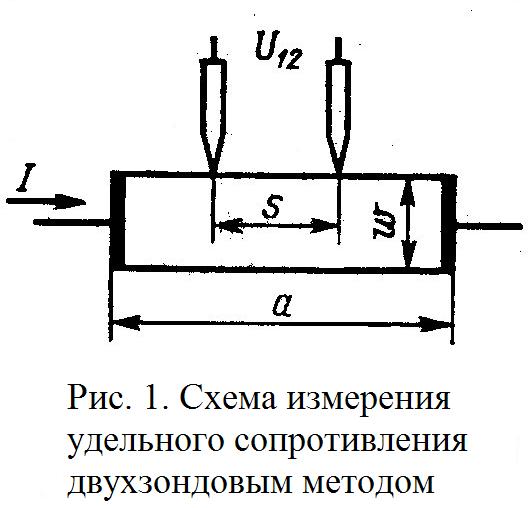 Двухзондовый метод применяют для измерения удельного сопротивления образцов, имеющих правильную геометрическую форму и постоянное поперечное сечение. При этом на торцевых гранях образца, например в виде прямоугольной пластины, изготавливают омические контакты. Через эти контакты вдоль обраца пропускают электрический ток. На одной из поверхностей образца вдоль линий тока устанавливают два контакта в виде металлических иголок – зондов, имеющих малую площадь соприкосновения с поверхностью и позволяющих измерить разность потенциалов (рис. 1). Если образец однороден, то его удельное сопротивление (Ом∙см) 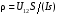 , ,где I – сила тока, протекающего через образец, A; U12 – разность потенциалов между измерительными или потенциальными зондами, В; s – расстояние между зондами, см; S – площадь поперечного сечения, см2. Неточное соблюдение геометрических размеров ведет к отклонению формы эквипотенциальных поверхностей от плоских поверхностей, параллельных торцевым граням образца, и возникновению систематической погрешности. Искажение формы эквипотенциальных поверхностей и одномерного пространственного распределения линий тока имеет место в образце правильной геометрической формы вблизи омических контактов, если они неоднородны по площади. На контакте металл – полупроводник при протекании электрического тока может возникать ряд физических эффектов и явлений, которые вносят существенную погрешность в результаты измерений. Основными из них являются: инжекция носителей заряда контактом, влияющая на проводимость образца; эффект Пельтье, приводящий к возникновению градиента температуры на образце и соответствующий этому градиенту термо-ЭДС; нагрев образца электрическим током, протекающим через образец. Указанные явления необходимо учитывать не только при измерении удельной проводимости, но и во всех случаях, когда через измеряемый образец с металлическими контактами протекает электрический ток. Чтобы уменьшить погрешности, вызванные этими явлениями, ток через образец выбирается минимальным, но обеспечивающим необходимую точность измерения тока и напряжения. Торцевые грани образца шлифуются абразивным порошком, после чего электролитически металлизируются. Абразивная обработка обеспечивает подавление инжекции носителей заряда. 3. ЧЕТЫРЕХЗОНДОВЫЙ МЕТОД ИЗМЕРЕНИЯ Четырехзондовый метод измерения удельного сопротивления полупроводников является наиболее распространенным. Кроме высоких метрологических показателей преимущество четырехзондового метода состоит в том, что для его применения не требуется создания омических контактов к образцу, возможно измерение удельного сопротивления объемных образцов самой разнообразной формы и размеров, а также удельного сопротивления слоев полупроводниковых структур. Условием для его применения с точки зрения формы образца является наличие плоской поверхности, линейные размеры которой превосходят линейные размеры системы зондов. Теория метода. Рассмотрим теоретические основы четырехзондового метода измерения удельного сопротивления применительно к образцу, представляющему собой полубесконечный объем, ограниченный плоской поверхностью. На плоской поверхности образца вдоль прямой линии размещены четыре металлических зонда с малой площадью соприкосновения (рис. 2), расстояния между которыми s1, s2, s3. Через два внешних зонда 1 и 4 пропускают электрический ток I14, на двух внутренних зондах 2 и 3 измеряют разность потенциалов U23. По измеренным значениям разности потенциалов между зондами 2 и 3 и тока, протекающего через зонды 1 и 4, можно определить удельное сопротивление образца. Чтобы найти аналитическую связь между удельным сопротивлением ρ, током I14 и напряжением U23, необходимо сначала решить более простую задачу, связанную с протеканием тока через отдельный точечный зонд, находящийся в контакте с плоской поверхностью полупроводникового образца полубесконечного объема (рис. 3). Линейное расположение зондов. Предположения, на которых основан четырехзондовый метод измерения удельного сопротивления: 1) зонды расположены на плоской поверхности однородного изотропного образца полубесконечного объема; 2) зонды имеют контакты с поверхностью образца в точках, которые расположены вдоль прямой линии; 3) инжекция носителей заряда в объем образца отсутствует. По принципу суперпозиции электрический потенциал в любой точке образца равен сумме потенциалов, создаваемых в этой точке током каждого зонда. При этом потенциал имеет положительный знак для тока, втекающего в образец (зонд 1), и отрицательный знак для тока, вытекающего из образца (зонд 4). Расположение зондов по вершинам квадрата. Линейное расположение зондов на поверхности полупроводникового образца не является единственно возможным. Можно, например, использовать систему четырех зондов, расположенных по вершинам квадрата. В этом случае ток пропускают через зонды, образующие одну из сторон квадрата, например через зонды 1 и 2, а напряжение измеряют на другой паре зондов 3 и 4. Используя соотношение (1), легко рассчитать, что при таком расположении зондов удельное сопротивление 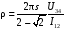 . .Расположение зондов по вершинам квадрата обеспечивает снижение случайных ошибок в два раза. Это достигается за счет выполнения измерений при пропускании тока последовательно через каждую пару соседних зондов, изменения полярности приложенного напряжения и последующего вычисления среднего значения удельного сопротивления по результатам восьми измерений. С помощью современной электронной измерительной аппаратуры такие измерения легко могут быть автоматизированы. Следует отметить, что высокое контактное сопротивление между зондом и образцом является одной из основных причин, ограничивающих применение четырехзондового метода для измерения удельного сопротивления широкозонных полупроводников типа А3В5 и А2В6. В технических условиях на монокристаллический кремний в слитках в соответствии с ГОСТ 19658—81 предусмотрена следующая методика измерения удельного сопротивления. Она распространяется на слитки монокристаллического кремния, получаемые по методу Чохральского и предназначенные для изготовления пластин-подложек, используемых в производстве эпитаксиальных структур и структур металл – диэлектрик – полупроводник. При выполнении всех требований к применяемым средствам измерения и соблюдении необходимых условий интервал, в котором находится случайная погрешность измерения удельного сопротивления, характеризующая сходимость результатов, равен ±2% при доверительной вероятности 0,95. Интервал, в котором находится погрешность измерения, определяющая воспроизводимость измерений при соблюдении требований стандарта, равен ±5% при доверительной вероятности 0,95. 4. МЕТОД ВАН-ДЕР-ПАУ 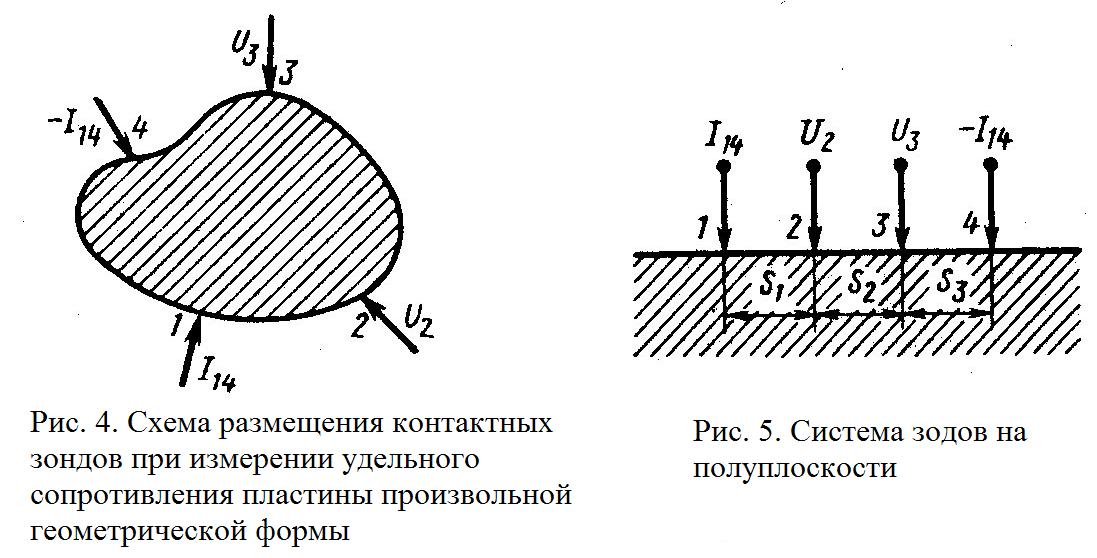 Удельное сопротивление образцов правильной геометрической формы, как отмечалось, можно рассчитать, вводя поправочные функции, учитывающие геометрическую форму и соотношение размеров образца. В общем случае для пластины произвольной геометрической формы расчет удельного сопротивления возможен при использовании видоизмененного четырехзондового метода измерения. В соответствии с этим методом по периметру плоской пластины вдоль образующих боковой поверхности размещают контакты 1—4 (рис. 4). Сначала пропускают ток через контакты 1 и 4, измеряют разность потенциалов между зондами 2 и 3 и вычисляют сопротивление 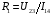 ; Затем пропускают ток через контакты 1 и 2 и по разности потенциалов между зондами 4 и 3 находят сопротивление ; Затем пропускают ток через контакты 1 и 2 и по разности потенциалов между зондами 4 и 3 находят сопротивление 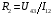 . Эти измерения позволяют рассчитать удельное сопротивление пластины. . Эти измерения позволяют рассчитать удельное сопротивление пластины.Чтобы получить аналитическое выражение, связывающее удельное сопротивление образца с измеряемыми величинами, рассмотрим случай пластины в виде полуплоскости. Пусть на боковой поверхности пластины находятся контакты 1—4. Через контакты 1 и 4 протекает ток 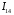 (рис. 5). (рис. 5).Схема измерения с помощью этого метода не отличается от схемы измерения четырехзондовым методом (см. рис. 2). 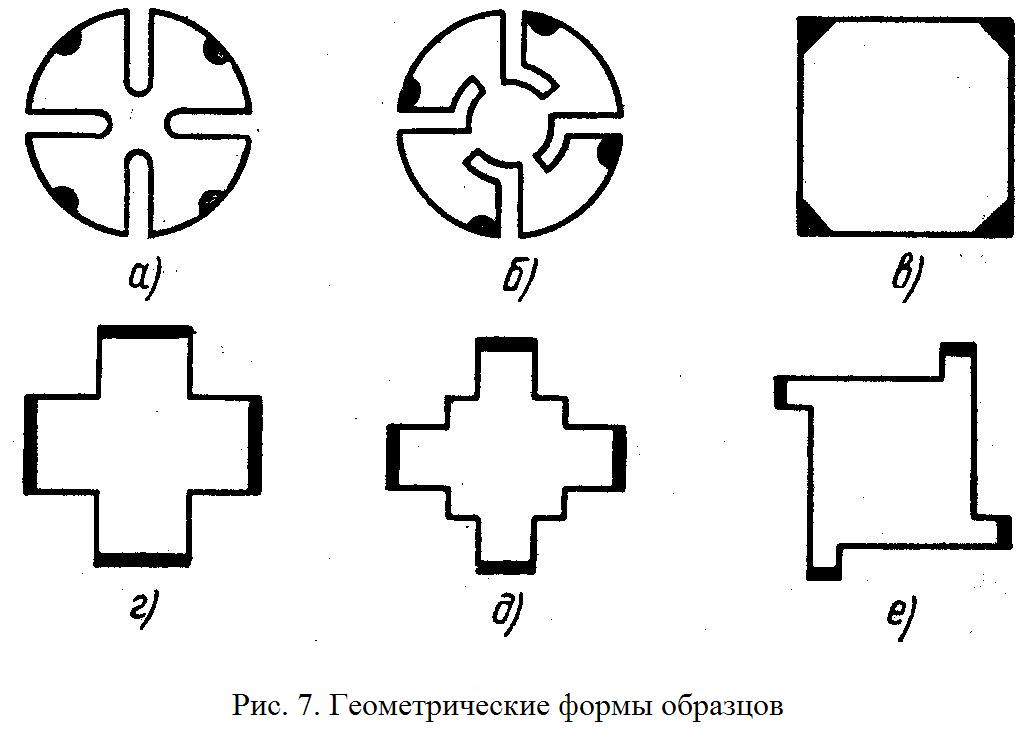 На основе рассмотренного метода разработаны автоматические устройства для разбраковки пластин на группы по значению удельного сопротивления. Образцы типа представленных на рис. 7, е используют для контроля микронеоднородностей поверхностного сопротивления диффузионных и ионно-легированных слоев, а также в качестве тестовых структур для контроля ухода размеров и совмещения рисунков при фотолитографии. 5. Анализ температурной зависимости холловской подвижности носителей заряда, полученной на основе экспериментальных данных по измерениям ЭДС Холла и удельной проводимости, представляет собой возможность определения концентрации электрически активных примесей в полупроводнике. Она связана с влиянием ионов примесных атомов на рассеяние носителей заряда, что в наибольшей степени сказывается на подвижности носителей заряда при низких температурах. Этот метод наиболее эффективен при высокой концентрации примесей, когда уширение возбужденных состояний приводит к образованию зоны непрерывного спектра, смыкающейся с исходной зоной. В этом случае раздельное определение концентрации доноров и акцепторов может быть осуществлено путем измерения холловской подвижности, если известны механизмы рассеяния носителей заряда. Наиболее полно метод определения полной концентрации примесей по подвижности носителей заряда разработан применительно к арсениду галлия n-типа; он имеет строгое количественное обоснование. Рассмотрим его применительно к арсениду галлия. В соединениях А3В5 зона проводимости параболическая, однако, вычисления подвижности электронов наталкиваются на трудности, связанные с необходимостью учета рассеяния носителей заряда на продольных оптических фононах, которое нельзя рассматривать в приближении времени релаксации. В наиболее простом случае концентрацию ионизированных примесей вычисляют по экспериментально измеренному значению подвижности носителей заряда при определенной температуре, комбинируя подвижность, связанную с рассеянием на ионах примеси и рассчитанную по формуле Брукса – Херринга, с подвижностью, обусловленной рассеянием носителей заряда кристаллической решеткой. Можно также анализировать подвижность, измеренную при такой низкой температуре (например, при 20 К), когда влияние полярного оптического рассеяния пренебрежимо мало. Для образцов с высокой концентрацией примеси при низкой температуре возможны прыжковая электропроводность, электропроводность по примесной зоне, вырождение полупроводника. Эти процессы ведут к тому, что измеренная при низкой температуре подвижность оказывается меньше подвижности при рассеянии носителей заряда ионами примеси. Для образцов с низкой концентрацией примеси подвижность носителей заряда при низкой температуре может быть меньше подвижности при рассеянии ионами примеси из-за влияния рассеяния на нейтральных атомах примеси или дефектах кристаллической решетки. Влияние этих механизмов рассеяния уменьшается с увеличением температуры, в то время как рассеяние кри сталлической решеткой становится сильнее. Поэтому должен существовать оптимальный интервал температур, в котором влияние рассеяния ионами примеси проявляется в наибольшей степени, а другие механизмы рассеяния оказывают минимальное воздействие на подвижность носителей заряда. Таким образом, анализ температурной зависимости подвижности носителей заряда с помощью формулы Брукса – Херринга позволяет выявить оптимальный температурный интервал и определить концентрацию ионов примеси. ИЗМЕРЕНИЕ ПОДВИЖНОСТИ НОСИТЕЛЕЙ ЗАРЯДА МЕТОДОМ ТОКА ХОЛЛА Эффект Холла можно исследовать не только с помощью традиционного измерения ЭДС Холла, но также с помощью определения тока Холла. Метод тока Холла был предложен и впервые реализован советскими учеными В. Н. Добровольским и Ю. И. Гриценко. Этот метод основан на измерении электри ческого тока, возникающего в образце при отклонении носителей заряда силой Лоренца, который по аналогии с электрическим полем Холла называют током Холла. Токовые металлические контакты закорачивают ЭДС Холла. По этой причине в приконтактной области образца магнитная составляющая силы, действующая на носители заряда, не компенсируется силой холловского электрического поля и носители заряда перемещаются под некоторым углом относительно продольного электрического поля. Электрическое поле Холла полностью закорачивается контактами у концов образца, имеет максимальное значение в его средней части. Электрический ток, наоборот, максимален у концов образца и минимален в его середине, так как поле Холла действует на носители заряда в направлении, противоположном силе Лоренца, уменьшая поперечную составляющую тока. Очевидно, что чем короче образец, тем сильнее шунтирующее действие токовых электродов. Для очень короткого образца холловское поле полностью закорочено и носители заряда перемещаются под действием силы Лоренца под углом Холла относительно внешнего электрического поля. Закорачивание поля Холла металлическими электродами лежит в основе зависимости ЭДС и тока Холла от соотношения геометрических размеров образца и определяет эффект геометрического магнитосопротивления. 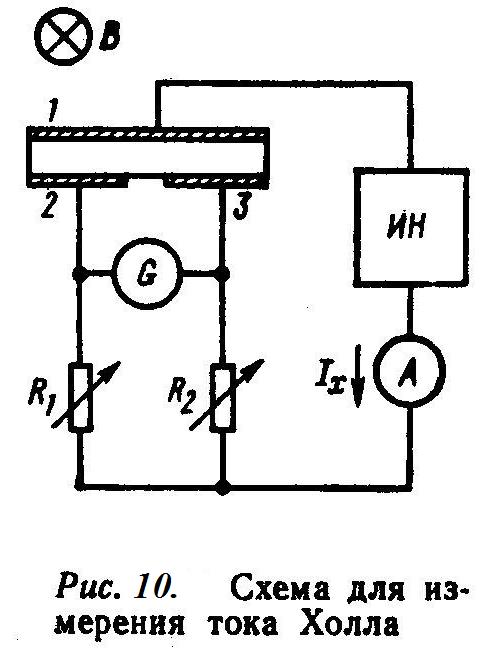 Рассмотрим схему, предназначенную для измерения тока Холла (рис. 10). Ток Холла равен сумме токов, протекающих вдоль токовых контактов; он может быть измерен, если расщепить токовые электроды и между их половинами включить токоизмерительные приборы. Поэтому основная особенность образца для измерения тока Холла заключается в том, что один из токовых контактов выполняют в виде двух равных половинок 2 и 3, разделенных узким за- ром. В отсутствие магнитного поля через образец протекает ток источника напряжения ИН. Если контакты 2 и 3 одинаковы и 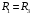 , то они эквипотенциальны и ток через гальванометр G протекает. При наличии тока через гальванометр, изменяя соротивления резисторов R1 и R2, можно довести его до нулевого значения. Чтобы весь ток Холла протекал через гальванометр и измерялся им, сопротивление гальванометра должно быть много меньше сопротивления области образца между контактами 2 и 3 сопротивлений R1 и R2. При соблюдении этих требований и наличии магнитного поля гальванометр покажет ток, равный 0,5Iy. Такой же ток потечет по контакту 1. , то они эквипотенциальны и ток через гальванометр G протекает. При наличии тока через гальванометр, изменяя соротивления резисторов R1 и R2, можно довести его до нулевого значения. Чтобы весь ток Холла протекал через гальванометр и измерялся им, сопротивление гальванометра должно быть много меньше сопротивления области образца между контактами 2 и 3 сопротивлений R1 и R2. При соблюдении этих требований и наличии магнитного поля гальванометр покажет ток, равный 0,5Iy. Такой же ток потечет по контакту 1.Метод тока Холла позволяет проводить измерения на более высокоомных материалах, чем метод ЭДС Холла. Этому способствует такое соотношение геометрических размеров образца, при котором его сопротивление между токовыми контактами ниже, чем при измерении ЭДС Холла. Небольшое различие в характеристиках половинок контактов практически не влияет на результаты измерений в высокоомных образцах, тогда как небольшая асимметрия в расположении холловских контактов при измерении ЭДС приводит к образованию их значительной неэквипотенциальности, которая затрудняет измерения. Так как ток, протекающий через поперечное сечение образца, складывается из объемной и поверхностной составляющих, то оказывается возможным разделить эти составляющие и исследовать их раздельно. С помощью рассматриваемого метода можно исследовать распределение подвижности носителей заряда вдоль неоднородного по длине канала МДП структур. Одно из преимуществ метода тока Холла состоит в том, что он менее подвержен влиянию захвата носителей заряда. Использование метода тока Холла ограничено в связи с жесткими требованиями, предъявляемыми к качеству омических контактов. Кроме того, данный метод подвержен влиянию контактных шумов, что обусловлено проведением измерений на тех же контактах, через которые течет продольный ток образца. Это обстоятельство также предопределяет повышенные требования к од нородности и сопротивлению контактов. |
