Ответы на вопросы к зачёту ФИЗИКА. 1. Физика и естествознание. Методы физического исследования эксперимент и теория в физических исследованиях. Единицы измерения и системы единиц. Основные единицы си

• Название: 1. Физика и естествознание. Методы физического исследования эксперимент и теория в физических исследованиях. Единицы измерения и системы единиц. Основные единицы си
• Дата: 14.10.2022
• Размер: 0.98 Mb.
• Имя файла: Ответы на вопросы к зачёту ФИЗИКА.docx
• Тип: Документы; #733678

1. Физика и естествознание. Методы физического исследования. эксперимент и теория в физических исследованиях. Единицы измерения и системы единиц. Основные единицы СИ.

В переводе с греческого «физика» - наука о природе.

Опыт – основной метод исследования в физике.

Опыт – это наблюдение исследуемого явления в точно контролируемых условиях, позволяющих следить за ходом явления и воссоздать его каждый раз при повторении этих условий.

Гипотеза - научное предположение, выдвигаемое для объяснения какого-либо факта или явления. Гипотеза подтверждается опытом.

Эксперимент - научно поставленный опыт с целью проверки гипотезы.

Физическая теория - система основных идей, обобщающих опытные данные и отражающих объективные закономерности природы.

Физическая теория дает объяснение целой области явлений природы с единой точки.

Система СИ определяет семь основных и производные единицы измерения, а также набор приставок. Установлены стандартные сокращённые обозначения для единиц измерения и правила записи производных единиц.

Основные единицы системы СИ: килограмм, метр, секунда, ампер, кельвин, моль и кандела. В рамках системы СИ считается, что эти единицы имеют независимую размерность, т. е. ни одна из основных единиц не может быть получена из других.

Производные единицы получаются из основных с помощью алгебраических действий, таких как умножение и деление. Некоторым из производных единиц в Системе СИ присвоены собственные названия.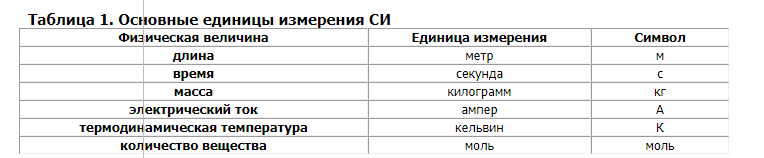



2. Предмет механики. Классическая и квантовая механика

Механика – наука б общих законах движения тел.

Квантовая механика – обширная область физики, изучающая законы природы, которые проявляются на малых расстояниях и при небольших энергиях атомов и субатомных частиц.

Классическая механика – это раздел классической физики, изучающий механическое движение макроскопических объектов, которые движутся со скоростями много меньше скорости света.

3. Основные механические модели: материальная точка, абсолютно твердое тело, сплошная среда.

Простейшая модель – это материальная точка – которой называется любое тело, размерами которого можно пренебречь.

Очень многие физические величины являются аддитивными (суммирование), поэтому можно рассматривать тела, которые не являются материальными точками, как системы материальных точек. Тогда, записав для каждой точки выражения для аддитивной величины можно эти выражения сложить и получить.

Системы материальных точек могут образовывать 2 вида моделей: абсолютно твердое тело, сплошная среда.

Абсолютно твердое тело – такая система материальных точек, в которой расстояние между материальными точками не изменяется, т.е. тело не деформируется ни при каких условиях.

Сплошная среда – это такая система материальных точек, в которой расстояние между двумя точками пренебрежительно мало.

4. Механическое движение как простейшая форма движения материи. Пространство и время как форма существования материя. Системы отсчета.

Простейшей формой движения материи является механическое движение, которое состоит в перемещении тел или их частей друг относительно друга.

Совокупность тел, выделенная для рассмотрения, называетсямеханической системой. Какие тела следует включить в систему, зависит от характера решаемой задачи.

Если мы собираемся изучать движение какого-либо тела, то обязательно нужно указать, по отношению к каким другим телам происходит данное движение.

Движение происходит как в пространстве, так и во времени (пространство и время — неотъемлемые формы существования материи). Поэтому для описания движения необходимо также определять время.

Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов образует систему отсчета.

Описать движение тела означает указать для каждого момента времени положение в пространстве и скорость тела. Для того чтобы задать состояние механической системы, нужно указать положения и скорости всех тел, образующих систему.

5. Основные кинематические характеристики движения частиц: перемещение, скорость, ускорение.

Траектория – линия, по которой движется матер. точка в пространстве.

Перемещение - изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Длина отрезка — это модуль перемещения, измеряется в метрах.

Скорость - векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта

Ускорение, производная скорости по времени — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).

6. Движение материальной точки по окружности. Угловая скорость и угловое ускорение, и их связь с линейными характеристиками движения.

Так как скорость - векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться.
Любое криволинейное движение можно свести к нескольким движениям по окружности. Примером данного движения является бег по стадиону, ход стрелки часов, прогулка на корде лошади и другое.

от угловой скорости или вторая производная от угла поворота по времени.

Угловая скорость – это значение, которое определяет, насколько изменяется угловое перемещение со временем. Угловое перемещение связано с линейной скоростью и центростремительным ускорением следующей формулой: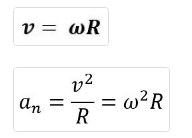



Угловое ускорение – величина, характеризующая изменение скорости с течением времени.

Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости.

7. Нормальное тангенциальное ускорения. Кинематика движения по криволинейной траектории.
Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.

Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки.

Частным случаем криволинейного движения – является движение по окружности. 

Нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению: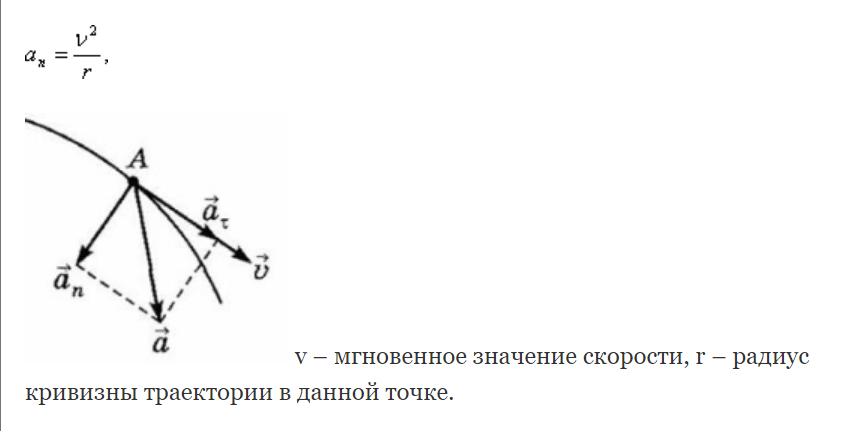



Тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.

8. Поступательное и вращательное движение абсолютно твердого тела.

Твердым телом называется физический объект, формы которого неизменны при любых воздействиях на него. Если взять произвольные две точки такого тела, то расстояние между ними всегда будет постоянным.
Движение тела можно назвать поступательным, если на данном теле можно провести прямую через две точки, которая будет двигаться параллельно своему предыдущему положению.


Вращательное движение вокруг оси - данный вид движения характеризуется двумя точками и прямой, которую можно провести через них - если прямая в теле остается неподвижной, а все остальные точки тела вращаются вокруг нее, то такое движение можно считать вращательным вокруг оси.



9. Потенциальная энергия заряда в электростатическом поле. Потенциал поля электростатического заряда.
Потенциальная энергия заряда, помещенного в любую точку пространства относительно нулевой точки, будет равна той работе, которая совершается электростатическим полем при перемещении заряда из этой точки в нулевую.
Потенциал электрического поля – это физическая величина, значение которой можно найти, разделив величину потенциальной энергии электрического заряда в электростатическом поле на величину этого заряда.

10. Первый закон Ньютона. инерциальные системы отсчета

Первый закон Ньютона

Существуют системы отсчета, называемые инерциальными. В таких системах отсчета тела движутся равномерно и прямолинейно или покоятся, если на них не действуют другие тела или если их действие скомпенсировано.

Инерция — это свойство тел сохранять свою скорость при отсутствии на него воздействий со стороны других тел. Именно поэтому второе название первого закона Ньютона - закон инерции.

11. Энергия как универсальная мера различных форм движения и взаимодействия, Кинетическая энергия механической системы и ее связь с работой внешних и внутренних сил, приложенных к системе
Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механи­ческую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движе­ния материи не изменяется (например, горячее тело нагревает холодное), в дру­гих — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той иди иной форме) одним телом другому телу, равна энергии, полученной последним телом. Кинетическая энергия механической системы — это энергия механического движения этой системы.

Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела, т. е.Ek=mv²/2.

12. Масса. Сила. Законы динамики материальной точки и системы материальных точек

Масса - количественная мера инерции тела. Она проявляется как мера инертности тела при попытке изменить его скорости.
Сила — это векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате, которого тело деформируется или приобретает ускорение.

Динамикой называется раздел теоретической механики, в котором изучается механическое движение материальных объектов в зависимости от физических факторов, то есть от причин, вызывающих это движение.

Напомним, что в классической механике движение материальных объектов рассматривается с помощью абстрактных моделей: материальной точки, механической системы и абсолютно твердого тела.

Материальная точка — это материальное тело, размерами и разницей в движении его частей которого можно пренебречь.

Механической системой (системой материальных точек) называется совокупность материальных точек, которые между собой взаимодействуют, то есть, положение и движение которых взаимосвязаны.

13. Импульс. Закон сохранения импульса.



Формулировка закона сохранения импульса (ЗСИ)

Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы.
Замкнутой изолированной системой называют такую, в которой тела взаимодействуют только друг с другом и не взаимодействуют с внешними телами.

14. Момент импульса. Момент силы. Закон сохранения момента импульса







15. Работа силы и ее выражение через криволинейный интеграл. мощность.

Если тело движется прямолинейно и на него действует постоянная сила F, составляющая некоторый угол α с направлением перемещения, то работа этой силы равна проекции силы F_s на направление перемещения (F_s= Fcosα), умноженной на соответствующее перемещение точки приложения силы:



Но на практике сила может изменяться как по модулю, так и по направлению, поэтому формула (1) непригодна. Однако, если рассмотреть данную ситуацию для элементарного перемещения dr, то силу F мы считаем постоянной, а движение точки ее приложения - прямолинейным. Элементарной работой силы F на перемещении dr называется скалярная величина



где α - угол между векторами F и dr; ds = |dr| - элементарный путь; Fs - проекция вектора F на вектор dr (рис. 1).



Если взять участок траектории от точки 1 до точки 2, то работа на нем равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Поэтому эту сумму можно привести к интегралу



где s - пройденный телом путь



16. Потенциальная энергия системы взаимодействующих тел. Потенциальная энергия материальной точки.

Потенциальная энергия – та часть энергии системы тел, которая определяется взаимным расположением входящих в систему тел или их частей и силами взаимодействия между ними.

Потенциальную энергию так же, как работу и кинетическую энергию, в СИ измеряют в джоулях.

Например, деформированная пружина обладает потенциальной энергией. Эта энергия равна работе, которую могут совершить силы упругости при возвращении пружины в недеформированное состояние. Потенциальную энергию недеформированной пружины считают равной нулю.

 Потенциальная энергия материальной точки, находящейся в каком-либо данном положении, равна работе силы потенциального поля при переходе точки из данного положения в нулевое.

17. Принцип относительности Галилея. Преобразования Галилея. Инварианты преобразования

Принципом относительности Галилея называется утверждение о том, что во всех инерциальных системах отсчета все механические и физические явления протекают одинаково.

Инерциальные системы отсчета- такие системы, которые движутся относительно друг друга с постоянной скоростью.

Системы отсчета называются инерциальными, если поля тяготения в них пренебрежимо малы, т.е. тела, удаленные достаточно далеко от других тел, движутся относительно таких координат равномерно и прямолинейно.

Допустим, что система отсчета S инерциальна, а S’ движется относительно нее поступательно вдоль оси Х со скоростью V. Выразим координаты x’ y’ z’ движущейся точки в системе S’ через координаты x y z в системе S в один и тот же момент времени. Пусть в момент времени t движущаяся точка находится в положении M.





Отсюда предыдущее выражение принимает вид



Запишем это соотношение в проекциях на координатные оси:



Формулы обратного преобразования имеют вид:





Эти формулы и называются преобразованием Галилея.

18. Закон сохранения энергии в механизме для замкнутых систем.
Механическая энергия замкнутой консервативной системы не изменяется в процессе ее движения:

c onst

19. Принцип относительности в релятивистской механике. Постулаты СТО.

20. Преобразования Лоренца для координат и времени и их следствия.

21. Относительность длин и промежутков времени.

22. Релятивистский импульс. Релятивистское выражение для кинетической энергии. Взаимосвязь массы и энергии.

23. Энергия покоя. Полная энергия частицы.

24. Уравнение движения твердого тела, вращающегося вокруг неподвижной оси. Вращательный момент

25. Момент инерции тела относительно оси. Момент инерции твердых тел разной формы.

уравнение Шредингера.

26. Идеально упругое тело. Деформация. Виды деформации.

27. Движение материальной точки по окружности. Угловая скорость и угловое ускорение, и их связь с линейными характеристиками движения.

28. Упругие деформации и напряжения. Закон Гука.

29. Трение. Виды трения. Силы трения.

30. Масса. Сила. Законы динамики материальной точки и системы материальных точек.

31. Работа силы и ее выражение через криволинейный интеграл. Мощность.

32. Механическое движение как простейшая форма движения материи. Пространство и время как формы существования материи. Системы отсчета.

33. Электрический заряд и его дискретность. Идеи близкодействия и дальнодействия.

34. Закон Кулона. Принцип суперпозиции полей.

35. Напряженность электрического поля. расчет электрических полей методом суперпозиции.

36. Плотность электрического заряда. Вектор электрического смещения.

37. Теорема Остроградского – Гаусса для электростатического поля в вакууме и ее применение к расчету поля (бесконечной заряженной плоскости).

38. Теорема Остроградского – Гаусса для электростатического поля в вакууме и ее применение к расчету поля (бесконечной заряженной нити).

39. Работа сил электростатического поля при перемещении заряда.

40. Связь между потенциалом и напряженностью электростатического поля.

41. Проводник в электростатическом поле. Электростатическая защита.

42. Электроемкость уединенного проводника. Конденсаторы. Электроемкость конденсаторов.

43. Энергия заряженного проводника.

44. Энергия заряженного конденсатора. Энергия электростатического поля.

45. Плотность энергии электростатического поля.

46. Проводники и изоляторы. Условия существования тока

47. Сила и плотность тока. Сопротивление.

48. Закон Ома для участка цепи. Дифференциальная форма закона Ома

49. Строение силы. Разность потенциалов, электродвижущая сила, напряжение. Источник тока.

50. Закон Ома для замкнутой цепи.

51. Работа и мощность электрического тока. Закон Джоуля – Ленца в интегральной и дифференциальной формах.

52. Магнитное поле проводника с током. Магнитная индукция

53. Действие магнитного поля на движущийся заряд. Сила Лоренца.

54. Движение заряженных частиц в магнитном поле.

55. Виток с током в магнитное поле. Магнитный момент, Момент сил, действующих на виток с током в магнитном поле.

56. Закон Био- Савара-Лапласа и его применение к расчету магнитных полей прямолинейного проводника с током.

57. Закон полного тока для магнитного поля в вакууме и его применение к расчету магнитного поля единого соленоида.

58. Контур с током в магнитном поле. Магнитный поток.

59. Явление электромагнитной индукции. закон электромагнитной индукции.

60. Явление самоиндукции. Индуктивность. Токи при замыкании и размыкании цепи.

61. Энергия магнитного поля проводника с током. объемная плотность энергии магнитного поля.

62. Вихревое электрическое поле. Ток смещения.

63. Система уравнений Максвелла в интегральной форме