шпоргалка. Шпоры_4семестр. 1 Мат методы, модели

• Название: 1 Мат методы, модели
• Анкор: шпоргалка
• Дата: 03.03.2023
• Размер: 0.52 Mb.
• Имя файла: Шпоры_4семестр.doc
• Тип: Закон; #966516
• страница: 2 из 5

18. Правила нахождения коэффициентов новой симплексной таблицы. Оценка оптимальности плана при решении задач на максимум и минимум целевой функции

Переходим к новой таблице по правилам:

1. в левом столбце записываем новый базис: вместо основной переменной X_q – переменную X_s

2. в столбцах, соответствующих основным переменным, проставляем нули и единицы:1 –против «своей» основной переменной, 0 –против «чужой» основной переменной, 0 – в последней строке для всех основных переменных

3. новую строку с номером q получаем из старой делением на разрешающий (ключевой) элемент a_qs

4. все остальные элементы a_ij` вычисляем по правилу прямоугольника:

Критерий оптимальности решения при отыскании максимума линейной функции: если в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то решение оптимально.

Критерий оптимальности решения при отыскании минимума линейной функции:

если в выражении линейной функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то решение оптимально.

Выполнение критерия оптимальности при решении задач на максимум – наличие в последней строке (F-базис) отрицательных коэффициентов b_i<0 (с_i>0). Если таких нет, то решение оптимально, достигнут max F=c₀, основные переменные принимают значения a_i0, основные переменные равны 0, т.е. получаем оптимальное базисное решение.

20. Двойственная задача линейного программирования. Характеристика основных соотношений оптимальных планов двойственной пары.
21. Двойственные задачи линейного программирования. Основные теоремы двойственных задач и их экономический смысл

22. Основные теоремы двойственности

Каждой задаче лин программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче. Дадим определение двойственной задачи по отношению к общей задаче лин программирования

(32)

при условиях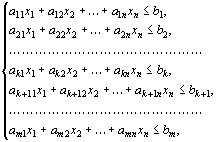

(33)

(34)

Определение.

Задача, состоящая в нахождении минимального значения функции

(35)

при условиях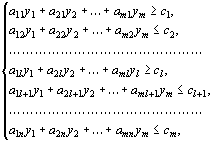

(36)

(37)

называется двойственной по отношению к задаче (32) – (34). Задачи (32) – (34) и (35) – (37) образуют пару задач, называемую в линейном программировании двойственной парой. Сравнивая две сформулированные задачи, видим, что двойственная задача составляется согласно следующим правилам:

1. Целевая функция исходной задачи (32) – (34) задается на максимум, а целевая функция двойственной (35) – (37) – на минимум.

2. Матрица

(38)

составленная из коэффициентов при неизвестных в системе ограничений (33) исходной задачи (32) – (34), и аналогичная матрица

(39)

в двойственной задаче (35) – (37) получаются друг из друга транспонированием (т. е. заменой строк столбцами, а столбцов – строками).

3. Число переменных в двойственной задаче (35) – (37) равно числу ограничений в системе (33) исходной задачи (32) – (34), а число ограничений в системе (36) двойственной задачи – числу переменных в исходной задаче.

4. Коэффициентами при неизвестных в целевой функции (35) двойственной задачи (35) – (37) являются свободные члены в системе (33) исходной задачи (32) – (34), а правыми частями в соотношениях системы (36) двойственной задачи – коэффициенты при неизвестных в целевой функции (32) исходной задачи.

5. Если переменная x_j исходной задачи (32) – (34) может принимать только лишь положительные значения, то j–е условие в системе (36) двойственной задачи (35) – (37) является неравенством вида “? ”. Если же переменная x_j может принимать как положительные, так и отрицательные значения, то 1 – соотношение в системе (54) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (33) исходной задачи (32) – (34) и переменными двойственной задачи (35) – (37). Если i – соотношение в системе (33) исходной задачи является неравенством, то i–я переменная двойственной задачи . В противном случае переменная у_j может принимать как положительные, так и отрицательные значения.

Двойственные пары задач обычно подразделяют на симметричн и несимметричн. В симметрич паре двойственных задач ограничения (33) прямой задачи и соотношения (36) двойственной задачи являются неравенствами вида “ ≤ ”. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.

Первая теорема двойственности:

Если одна из взаимно двойственных задач имеет оптим решение, то его имеет и другая, причем оптимальные значения их линейных функций равны:

F_max=Z_min или F(X*)=Z(Y*)

Экономический смысл:

План производства Х*=(х₁*, х₂*,…,х_n*) и набор цен (оценок) ресурсов Y*=(y₁*,y₂*,…,y_m*) оказывается оптим тогда и только тогда, когда прибыль (выручка) от продукции, найденная при «внешних» (известных заранее) ценах с₁, с₂,…,c_n, равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам y₁, y₂,…,y_m. Для всех же др планов Х и Y обеих задач в соответствии с осн неравенством теории двойственности прибыль от продукции всегда меньше (или равна) затрат на ресурсы.

Вторая теорема двойственности:

Компоненты оптим решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные ее оптимального решения.

Эк интерпретация: Предположим, что некоторая организация решила закупить ресурсы S1, S2,…, Sm предприятия и необходимо установить оптимальные цены на эти ресурсы y1, y2,…,ym были минимальны, т.е. Z=b1y1+b2y2+…+bmym->min

С другой стороны, предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не менее той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции Р1 расходуется а11 единиц ресурса S1, a21 единиц ресурса S2, …, ai1 единиц ресурса Si, …, am1 единиц ресурса Sm по цене соответственно y1, y2, …, yi, …, ym. Поэтому для удовлетворения требований продавца затраты на ресурсы, потребляемые при изготовлении единицы продукции Р1, должны быть не менее ее цены с1, т.е. a11y1+a21y2+…+am1ym c1.

Аналогично можно составить ограничения в виде неравенств по каждому виду продукции Р1, Р2, …, Рn. Экономико-математическая модель и содержательная интерпретация полученной таким образом двойственной задачи II приведены в правой части таблицы

23. Типы уравнений-ограничений задачи при решении задач целочисленного программирования.
По смыслу значит части экономич задач, относящихся к задачам лин программир, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, напр задачи, в которых переменные означают количество единиц неделимой продукции, число судов при распределениях по линиям, число турбин в энергосистеме, число вычислит машин в управляющем комплексе и мн др.

Задача лин целочисл программирования формулируется следующим образом: найти такое решение (план) Х=(х₁, х₂, …, х_n), при котором линейная функци

принимает макс или мин значение при ограничениях , i=1, 2, …, m

, j= 1, 2,…,n. X_j- целые числа.

Для решения задач лин целочисл программирования используется ряд методов. Самый простой из них – обычный метод лин программирования. В случае если компоненты оптим решения оказываются нецелочисленного, их округляют до ближайших целых чисел. Этот метод применяют тогда, когда отдельная единица совокупности составляет малую часть объема всей совокупности. В противном случае округление может привести к далекому от оптим целочисл решению, поэтому используют спец разработанные методы. Методы целочисл оптимизации можно разделить на 3 основные группы: 1.методы отсечения 2.комбинаторные методы 3.приближенные методы.

Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисл. Если полученный план целочис, задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами: оно должно быть линейным, должно отсекать найденный оптимальный нецелочисленный план, не должно отсекать ни одного целочисленного плана.

Доп ограничение, обладающее указанными свойствами, называется правильным отсечением. Далее задача решается с учетом нового ограничения. После этого в случае необходимости добавляется еще одно ограничение итп.

Геометрич добавление каждого лин ограничения отвечает проведению прямой (гиперплоскости), которая отсекает от многоугольника (многогранника) решений некоторую его часть вместе с оптим точкой с нецелыми координатами, но не затрагивает ни одной из целых точек этого многогранника. В результате новый многогранник решений содержит вес целые точки, заключавшиеся в первоначальном многограннике решений и соответственно полученное при этом многограннике оптим решение будет целочисленным.
24 Графо-аналитический метод решения задач целочисленного программирования. Область допустимых решений. Случаи множества равноценных оптимальных планов.
Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисленности. Если полученный план целочисленный, задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:

• 
  оно должно быть линейным
  
• 
  должно отсекать найденный оптимальный нецелочисленный план
  
• 
  не должно отсекать ни одного целочисленного плана
  

Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением. Далее задача решается с учетом нового ограничения. После этого в случае необходимости добавляется еще одно ограничение итп.

Геометрическое добавление каждого линейного ограничения отвечает проведению прямой (гиперплоскости), которая отсекает от многоугольника (многогранника) решений некоторую его часть вместе с оптимальной точкой с нецелыми координатами, но не затрагивает ни одной из целых точек этого многогранника. В результате новый многогранник решений содержит вес целые точки, заключавшиеся в первоначальном многограннике решений и соответственно полученное при этом многограннике оптимальное решение будет целочисленным.
25. Основные этапы решения целочисленных задач методом Р.Гомори, области применения этого класса задач в экономике.
По смыслу значительной части экономических задач, относящихся к задачам линейного программирования, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, например, задачи, в которых переменные означают количество единиц неделимой продукции, число судов при распределениях по линиям, число турбин в энергосистеме, число вычислительных машин в управляющем комплексе и многие другие.

Задача линейного целочисленного программирования формулируется следующим образом: найти такое решение (план) Х=(х₁, х₂, …, х_n), при котором линейная функци

принимает максимальное или минимальное значение при ограничениях , i=1, 2, …, m

, j= 1, 2,…,n. X_j- целые числа.

Один из алгоритмов решения задачи линейного целочисленно­го программирования (2.4.2)-(2.4.4), предложенный Гомори, основан на симплексном методе и использует достаточно простой способ построения правильного отсечения.

Пусть задача линейного программирования (2.4.1)-(2.4.3) име­ет конечный оптимум и на последнем шаге ее решения сим­плексным методом получены следующие уравнения, выра­жающие основные переменные х₁, х₂, ..., x_j..., x_m через неос­новные переменные x_m+1, x_m+2,…, x_m+i, …, x_n  оптимального решения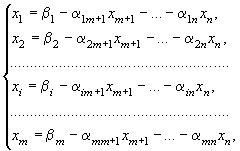

                (2.4.5)

так, что оптимальным решением задачи (2.4.1)-(2.4.3) является Х^* = (β₁, β₂, …, β_i, …β_m,0,0,…,0), в котором, например β­_i - нецелая компонента. В этом случае можно доказать, что неравен­ство

              (2.4.6)

сформированное по i-му уравнению системы (2.4.5), обладает всеми свойствами правильного отсечения.

Для решения задачи целочисленного линейного программиро­вания (2.4.1)-(2.4.4.) методом Гомори используется следующий ал­горитм:

- симплексным методом решается задача (2.4.1)-(2.4.3) без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочис­ленного программирования (2.4.1)-(2.4.4). Если первая задача (2.4.1)-(2.4.3) неразрешима (т.е. не имеет конечного оптимума или условия ее противоречивы), то и вторая задача (2.4.1)-(2.4.4) также неразре­шима;

- если среди компонент оптимального решения есть неце­лые, то выбирается компонента с наибольшей целой частью и по соответствующему уравнению системы (2.4.5) формируется пра­вильное отсечение (2.4.6);

- неравенство (2.4.6) путем введения дополнительной неотрицатель­ной целочисленной переменной преобразовывается в равносильное уравнение

           (2.4.7)

 и включается в систему ограничений (2.4.2);

- полученную расширенную задачу решают симплексным ме­тодом. Если найденный оптимальный план будет целочисленным, то задача целочисленного программирования (2.4.1)-(2.4.4) решена. В противном случае следует вернуться к пункту 2 алгоритма и повторить цикл до тех пор, пока не будет получен оптимальный план .

Если задача разрешима, то оптимальный целочисленный план будет найден после конечного числа шагов (итераций).

Если в процессе решения появится уравнение (выражающее основную переменную через неосновные) с нецелым свободным членом и целыми остальными коэффициентами, то соответст­вующее уравнение не имеет решения в целых числах. В этом слу­чае и данная задача не имеет целочисленного оптимального ре­шения.


26. Правила составления дополнительного условия Гомори. Дробная часть чисел в условии Гомори. Правила расчета новых таблиц двойственным симплексным методом.
Для решения задачи целочисленного линейного программиро­вания (2.4.1)-(2.4.4.) методом Гомори используется следующий ал­горитм:

- симплексным методом решается задача (2.4.1)-(2.4.3) без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для задачи целочис­ленного программирования (2.4.1)-(2.4.4). Если первая задача (2.4.1)-(2.4.3) неразрешимна (т.е. не имеет конечного оптимума или условия ее противоречивы), то и вторая задача (2.4.1)-(2.4.4) также неразре­шима;

- если среди компонент оптимального решения есть неце­лые, то выбирается компонента с наибольшей целой частью и по соответствующему уравнению системы (2.4.5) формируется пра­вильное отсечение (2.4.6);

- неравенство (2.4.6) путем введения дополнительной неотрицатель­ной целочисленной переменной преобразовывается в равносильное уравнение

           (2.4.7)

 и включается в систему ограничений (2.4.2);

- полученную расширенную задачу решают симплексным ме­тодом. Если найденный оптимальный план будет целочисленным, то задача целочисленного программирования (2.4.1)-(2.4.4) решена. В противном случае следует вернуться к пункту 2 алгоритма и повторить цикл до тех пор, пока не будет получен оптимальный план .

Если задача разрешима, то оптимальный целочисленный план будет найден после конечного числа шагов (итераций).

Если в процессе решения появится уравнение (выражающее основную переменную через неосновные) с нецелым свободным членом и целыми остальными коэффициентами, то соответст­вующее уравнение не имеет решения в целых числах. В этом слу­чае и данная задача не имеет целочисленного оптимального ре­шения.

Задачи линейного программирования можно решать двойственным симплексным методом. Системы ограничений в задачах при положительном базисе имеют свободные члены любого знака. Двойственный симплексный метод позволяет значительно уменьшить размеры симплексной таблицы и количество преобразований системы ограничений. Для получения решения исходной задачи можно перейти к двойственной. А используя оценки ее оптимального плана, можно определить оптимальное решение исходной задачи.

Если рассмотреть первую симплексную таблицу с единичным дополнительным базисом, тогда переход к двойственной задаче не обязателен. Это связано с тем, что в столбцах определена исходная задача, а в строках - двойственная.

b_i являются оценками плана двойственной задачи. С_j являются оценками плана исходной задачи.

Найдем решение двойственной задачи по симплексной таблице. В симплексной таблице прописана исходная задача. Также определим оптимальный план двойственной задачи. Также найдем и оптимальный план исходной задачи.

Такой метод принято называть двойственным симплексным методом.

Допустим нужно определить исходную задачу линейного программирования, которая поставлена в общем виде: минимизировать функцию Z=СХ при АХ=A₀, Х>0. Значит в двойственной задаче следует максимизировать функцию f=YA₀ при YA>С. Пусть определен следующий базис D=(A₁, А₂,…, А_i,…, А_m), причем в нем хотя бы одна из компонент вектора Х=D^-1A₀=(x₁, x₂,…, x_i,…, x_m) отрицательная. Для всех векторов A_j используется следующее соотношение Z_j-C_j >0 (i=1,2,…, n).

Пользуясь теоремой двойственности, Y=С_базD^-1 является планом двойственной задачи. Этот план не оптимальный. Потому что оценки оптимального плана двойственной задачи должны быть неотрицательными и выбранный базис X содержит отрицательную компоненту и не является планом исходной задачи, а с другой стороны.

Поэтому, следует исключить из базиса исходной задачи вектор А_i, который соответствует компоненте x_i<0. Данный вектор относится к отрицательной оценке, его необходимо включить в базис двойственной задачи.

Просматриваем i-ю строку для выбора вектора, включаемого в базис исходной задачи. Т.е. если строка не имеет x_ij<0, тогда линейная функция двойственной задачи не ограничена на многограннике решений. Поэтому нет решений исходной задачи.

В противном случае для столбцов, имеющих отрицательные значения, определяем q_0j=min(x_i/x_ij)>0. Также находим вектор, который соответствует minq_0j(Z_j-C_j) при решении исходной задачи на максимум, а также maxq_0j(Z_j-C_j) при значении исходной задачи на минимум.

Найденный вектор включаем в базис исходной задачи. Направляющей строкой определяется вектор, который надо убрать из базиса исходной задачи.

Допустим, что q_0j=min(x_i/x_ij)=0, т.е. x_i=0, тогда x_ij выбирается как разрешающий элемент, но лишь тогда, когда x_ij>0.

Данный подход к решению задачи не приводит к росту количества отрицательных компонент вектора X. Пока не будет получено Х>0, процесс не прекращается.

Определяя оптимальный план двойственной задачи, находим и оптимальный план исходной задачи.

Используя при решении, алгоритм двойственного симплексного метода условие Z_j-C_j>0 допускается не учитывать, пока не будут исключены все х_i<0.

Обычным симплексным методом определяется оптимальный план. Этот метод обычно используется при условии, что все х_i<0. Чтобы перейти к плану исходной, задачи за одну итерацию надо определить q_0j=max(x_i/x_ij)>0.